|
|
ответы дет.маш. ответы дет. Техническое задание (ТЗ) Документ содержащий назначение, технические характеристики и показатели качества, т
§ 9.8. Тепловой расчет, охлаждение и смазка передачи
Механическая энергия, потерянная в передаче, превращается в тепловую и нагревает передачу. Если отвод теплоты недостаточный, передача перегревается и выходит из строя. Количество теплоты, выделяющейся в передаче в секунду, или тепловая мощность,

где Рх—мощность на входном валу, Вт; η— КПД передачи.
Через стенки корпуса редуктора теплота отдается окружа¬ющему воздуху, происходит естественное охлаждение. Коли¬чество теплоты, отданной при этом в секунду, или мощность теплоотдачи,
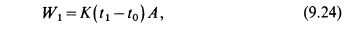
где А—площадь поверхности охлаждения, м2; tx—внутренняя температура редуктора или температура масла, °С;
t0 — температура окружающей среды (воздуха), сС; К—коэф¬фициент теплоотдачи, Вт/(м2 °С).
Под площадью поверхности охлаждения А понимают только гу часть площади наружной поверхности корпуса редуктора, которая изнутри омывается маслом или его брыз¬гами, а снаружи — свободно циркулирующим воздухом. По последнему признаку обычно не учитывают площадь по¬верхности днища корпуса. Если корпус снабжен охлаждаю¬щими ребрами, то учитывают только 50% площади их поверхности.
Глобоидные передачи. Особенности конструкции и расчета;
Из червячных редукторов наиболее распространены в настоящее время редукторы с цилиндрическими и глобоидными червяками. Передаточное отношение одной червячной передачи от 8 до 100, а иногда может доходить до 1000, что позволяет получить компактную конструкцию редуктора. В червячных редукторах в течение продолжительного времени применялись исключительно червячные передачи с цилиндрическим червяком ввиду их простоты в изготовлении и регулировке. Цилиндрический червяк червячной передачи представляет собой винт с резьбой различного профиля, наружная поверхность витков которого имеет форму цилиндра. По форме профиля витка червяки бывают архимедовы, конволютные и эвольвентные. Архимедовы червяки (Рис. 8,а) имеют в осевом сечении витка трапецеидальный профиль, а в торцовом сечении очерчены архимедовой спиралью. Изготавливаться эти червяки могут па обычных токарно-винторезных станках, что определило их широкое распространение. Применяются архимедовы червяки в основном без шлифовки, так как требуют специально профилированного шлифовального круга. В связи с возросшими требованиями к червячным передачам этот тип червяка в настоящее время находит применение в основном при мелкосерийном производстве.
Конволютный червяк (Рис. 8,б) имеет прямолинейные очертания витка в нормальном сечении. Технология изготовления этих червяков проще, чем архимедовых. При шлифовке конволютного червяка на обычном резьбошлифовальном станке получается нелинейчатый профиль витка, близкий к поверхности конволютного червяка.
Эвольвентные червяки (Рис. 8,б) имеют прямолинейный профиль при сечении витка плоскостью, касательной к основному цилиндру червяка, а при сечении плоскостью, перпендикулярной к оси, дают эвольвенту. Эвольвентные червяки допускают шлифовку винтов червяка торцом шлифовального круга. Поэтому такой вид червячной передачи особенно выгодно применять при крупносерийном производстве .
Число заходов червяка в силовых передачах обычно выбирают в пределах от 1 до 4, а количество зубьев червячного колеса — от 26 до 80. При выборе числа зубьев колеса и количества заходов червяка нестандартных передач можно руководствоваться табл. 9.
Кинематические параметры и принцип действия волновых передач;
Вращение генератора вызывает вращение жесткого колеса с угловой скоростью соь (вариант I) или гибкого колеса с а>0 (вариант И).
Условимся называть: w0—размер деформирования, равный радиальному перемещению точки гибкого колеса по большой оси генератора; большая и малая оси генератора — большая и малая оси формы деформирования гибкого колеса в торцовом сечении.
§ 10.2. Кинематические параметры и принцип действия
Передаточное отношение найдем, используя метод Виллиса (см. § 8.15):

После преобразования получим:
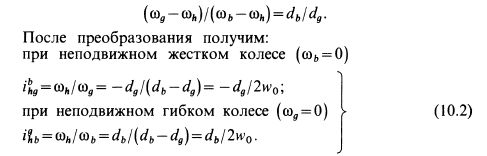
В простой передаче i равно отношению радиусов, а в вол¬новой— отношению радиуса ведомого колеса к разности радиусов или к размеру деформирования w0.
Очевидно, что разность радиусов можно выполнить малой, а /—большим. Большое i—одно из положительных качеств волновой передачи. Значение /тах для фрикционных передач
ограничивается точностью изготовления или допускаемыми отклонениями размеров диаметров. Практически выполняют 'max ^ ЮОО. Значение /min ограничивает прочность гибких колес, так как значение напряжения пропорционально размеру деформирования w0. При стальных гибких колесах /min^80. Ограничение /min- один из недостатков волновых передач.
По структуре волновая передача, так же как и планетарная, является трехзвенным механизмом. Она может работать не только в режиме редуктора или мультипликатора, но и в ре¬жиме дифференциала.
Метод Виллиса позволяет просто получить формулы для передаточных отношений, но не вскрывает принципа преобразования параметров движения путем деформирования гиб¬кого звена механизма.
Действительно, в передачах с жесткими звеньями, например в простой фрикционной передаче, при вращении одного колеса точки его поверхности получают окружную скорость, и если к этому колесу прижать другое, то оно получит ту же окружную скорость, а угловые скорости колес будут обратно пропорциональны их радиусам.
Как же образуются окружные скорости в волновой передаче? Как вращение генератора передается жесткому колесу через невращающееся гибкое колесо?
Для того чтобы выяснить это, рассмотрим движение точек невращающегося гибкого колеса при его деформировании вращающимся генератором. Отметим, что в нашей конструкции гибкое колесо подобно оболочке (толщина значительно меньше других размеров).
Передаточное отношение и число зубьев зубчатой волновой передачи;
передаточное отношение составит
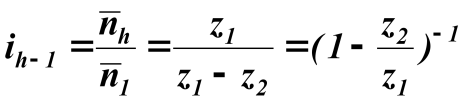 ; (8.14) ; (8.14)
а с учётом одинаковости модуля зацепляющихся колёс
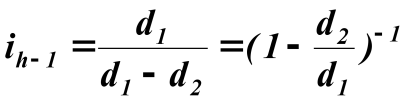 . (8.14а) . (8.14а)
Рассматривая аналогичным образом передачу движения в редукторе с неподвижным гибким колесом и подвижным, связанным с выходным валом, жёстким колесом не трудно установить, что передаточное отношение
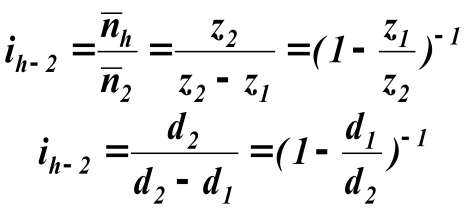 . (8.15) . (8.15)
Разность в числах зубьев жесткого и гибкого колёс с целью исключения интерференции зубьев должна быть пропорциональна числу волн волнового генератора.
КПД волновых передач относительно высок и также как в планетарных передачах падает с увеличением передаточного числа, а с увеличением нагрузки вначале растёт до максимально возможной величины, а потом, при дальнейшем возрастании нагрузки, начинает резко снижаться. При оптимальной нагрузке в пределах передаточного числа 80u250 коэффициент полезного действия 0,90,8.
Относительное движение зубьев, выбор профиля и размеров зубьев;
Разработано несколько профилей зубьев для волновых передач. Преимущественное распространение получили эвольвентные зубья, как наиболее технологичные и обеспечивающие удовлетворитель�ное зацепление. При большом числе зубьев волновых передач (обы�чноZ> 150) форма эвольвентного зуба близка к трапецеидальному.
При использовании распространенного двадцатиградусного ис�ходного контураугол профиля & варьируют путем смещения инст�румента при нарезании, приспосабливая его к условиям зацепления.Синтез зацепления выполняют на основе анализа относительного движения зубьев.
На рис. 10.3 изображена траектория движения точки срединной поверхности гибкого колеса. Уравнения этой траектории можйо использовать для построения графика относительного движения зубьев в процессе зацепления.
На рис. 10.6 показано взаимное положение зубьев на малой оси генератора в момент времени /=0. Штриховой линией изображено положение зуба колесаG до деформирования. Здесьг — радиус срединной поверхности; ось п совпадает с осями симметрии зубьев; rag, Гаь — радиусы окружностей вершин зубьев;Rfg, — радиусы окружностей впадин.
Положение зуба колесаЬ в осях координатп —T определяем по двум точкам, взятым на оси симметрии и соответствующим окру�жностям вершин и впадин. Координаты по оси п
КПД и критерии работоспособности зубчатой волновой передачи;
КПД. Исследованиями установлено, что основными составля�ющими потерь мощности в волновой передаче являются потери в зубчатом зацеплении и генераторе. Несмотря на значительную нагрузку зацепления, обусловленную большими передаточными от�ношениями, реализуемыми в одной ступени волновой передачи, потери здесь сравнительно невелики, так как невелики скорости скольжения. Значительная доля потерь приходится на генератор как элемент конструкции, вращающийся с высокой скоростью входного звена и воспринимающий большие нагрузки выходного звена. Так же как и в простых передачах, КПД растет с увеличением нагрузки и уменьшается с увеличением передаточного отношения. Замечено, что КПД имеет максимум при некоторой величине нагрузки. Поло�жение максимума зависит от жесткости звеньев передачи. При увеличении жесткости максимум сдвигается в сторону больших нагрузок (вследствие уменьшения искажения формы звеньев под нагрузкой), что влияет на качество зацепления. Практически КПД при /«80...250 располагается в пределах 0,9...0,8 соот�ветственно.
Основные критерии работоспособности — прочность гибкого ко�леса; прочность гибкого подшипника генератора; жесткость генера�тора и жесткого колеса; износ зубьев. Первые два критерия не требуют дополнительных пояснений. Чрезмерное деформирование генератора и жесткого колеса приводит к интерференции зубьев при входе в зацепление и вращению (проскакиванию) генератора при неподвижном выходном вале. Износ зубьев при правильно выбран�ных геометрии зацепления, материале, термообработке и удовлет�ворительной смазке незначителен и практически не ограничивает срок службы передачи
Основные типы фрикционных передач и вариаторов. Особенности геометрии и кинематики;
Во фрикционной передаче с гладкими цилиндрическими катками (см. рис. 11.1)
/=пхп2=d2j[dx(1 - в)]« d^duFn=KFJf,
Где 0,01...0,03 — коэффициент скольжения;К — запас сцепления;
1,25...1,5 для силовых передач; Кя 3 для передач приборов.
Коэффициент трения / во фрикционных передачах для разных случаев принимают:
Сталь по стали в масле 0,04...0,05;
Сталь по стали или чугуну без смазки 0,15...0,20;
Сталь по текстолиту или фибре без смазки/«0,2...0,3.
Формула (11.4) позволяет отметить, что сила прижатия катков фрикционной передачи велика. Например, принимая/=0,1 иК= 1,5, получаем ^„=15Fh тогда как в зубчатых передачах нагрузка в зацеп�лении примерно равнаFt.
Для передачи движения между валами с пересекающимися ося�ми используют коническую фрикционную передачу (рис. 11.3). Угол £ между осями валов может быть разным, чаще всего он равен 90°. Без учета проскальзывания передаточное отношение
Учитывая, чтоD2=2Rsind29 a rf, = 2i? sin<51, для конической пере�дачи получаем
Z'=sin (52/sin и при Z = <51 + <52=90°,
Z=Tg<52 =Ctg<5,.
Необходимые величины сил прижатияFt иF2 определяют из уравнений
KF, =fFn=/F,/sin<5ьKF,=fF2/sm52.
Из формул (11.6) с учетом (11.5) следует, что с увеличением передаточного отношения уменьшаетсяFi и увеличиваетсяF2. Поэ�тому в понижающих конических передачах прижимное устройство целесообразно устанавливать на ведущем валу.
Лобовой вариатор (см. рис. 11.2). Максимальное и минимальное передаточные отношения
*тах —п1Mfrmn^ ^2тах/DJ
*'min= Щ/Щтах. тш/d
Диапазон регулирования
D= /щах/ W=^2max/^2min=^2 max/^2min*
Диапазон регулирования является одной из основных характери�стик любого варианта.
Теоретически для лобового вариатора можно получить rf2min-*0, а 2)->оо. Практически диапазон регулирования ограничивают 2)^3. Это объясняется тем, что при малыхd2 значительно возрастает скольжение и износ, а КПД понижается (см. § 11.3).
В отношении КПД и износостойкости лобовые вариаторы усту�пают другим конструкциям. Однако простота и возможность ревер�сирования обеспечивают лобовым вариаторам достаточно широкое применение в маломощных передачах приборов и других подобных устройствах. Для повышения диа�пазона регулирования применяют двухдисковые лобовые вариаторы с промежуточным роликом (см. рис. 11.7, б). В этих вариаторах получают D = 8...10.
Критерии работоспособности и расчета фрикционной передачи;
Для фрикционных передач с металлическими катками основным критерием работоспособности является контактная прочность. Прочность и долговечность фрикционных передач оцениваются по контактным напряжениям — напряжениям смятия поверхности на площадке контакта. Расчет па прочность фрикционной передачи. Контактные напряжения передач с контактом по линии определяют по формуле Герца
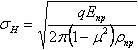 (2.2.5), (2.2.5),
где Q — сила прижатия катков;
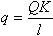 ; ;
К — коэффициент запаса сцепления (коэффициент нагрузки), К= 1,25...2;
l— длина контактной линии;
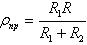 — приведенный радиус кривизны: — приведенный радиус кривизны: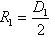 , ,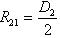
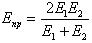 — приведенный модуль упругости, — приведенный модуль упругости,
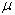 - коэффициент Пуассона - коэффициент Пуассона
Расчет фрикционных передач на прочность;
Фрикционными называют передачи, в которых силовое взаимодействие жёстких
звеньев осуществляется за счёт сил трения. Их применяют для передачи движения
между валами с параллельными и пересекающимися осями, а также для преобразования
вращательного движения в поступательное или винтовое.
Рабочие поверхности металлических катков фрикционных передач, работающих в
масле при жидкостном трении, разрушаются из-за усталостного выкрашивания под
действием переменных контактных напряжений, вызванных силой нажатия. Установлено,
что долговечность катков связана с максимальным контактным напряжениям 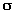 Н, Н,
определяемым по формуле Герца-Беляева,
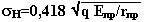
где q- погонная нагрузка (нагрузка на единицу длины), Епр= 2 Е1Е2/(Е1+Е2)-
приведённый модуль упругости для материалов катков; rпр- приведённый радиус
кривизны поверхностей катков в точке контакта, rпр= r1r2/(r1+r2). Здесь Еi,
ri - модуль упругости и радиус кривизны соответствующего катка в точке контакта.
В передачах, работающих без смазывания или при смазывании, но без
обеспечения режима жидкостного трения, выход катков из строя происходит из-за
их изнашивания, интенсивность которого пропорциональна величинам 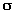 Н и Н и
коэффициента трения f. Поэтому расчёт передач выполняют на основе условия
контактной прочности
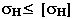
где [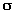 Н] - допускаемое контактное напряжение, принимают равным 800...1200 МПа Н] - допускаемое контактное напряжение, принимают равным 800...1200 МПа
для металлической пары, а для катков из текстолита при работе без смазывания
оно равно 80... 100 МПа.
При проектном расчёте в качестве первого расчётного параметра для передач
с гладкими цилиндрическими катками принимают межосевое расстояние, мм
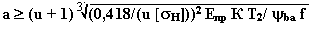
где К- коэффициент запаса сцепления, принимаемый в пределах 1,25-1,5 в силовых
передачах и К=3 в приборах; T2 - вращающий момент ведомого катка, Н м,
u - передаточное отношение передачи, 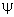 ba-коэффициент ширины b катка, ba-коэффициент ширины b катка,
 ba= b/a = 0,2...0,4 ; f- коэффициент трения, f=0,5 для пары катков из стали и ba= b/a = 0,2...0,4 ; f- коэффициент трения, f=0,5 для пары катков из стали и
чугуна при работе в масле, f= 0,15...0,2 для той же пары при работе всухую,
f= 0,1...0,35 для пары сталь-текстолит или чугун-текстолит при работе всухую.
|
|
|
 Скачать 0.97 Mb.
Скачать 0.97 Mb.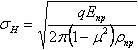 (2.2.5),
(2.2.5),
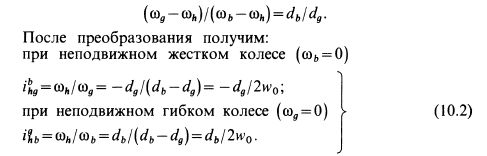

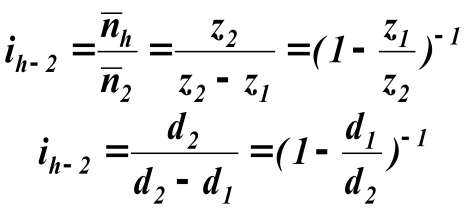 . (8.15)
. (8.15)