ответы дет.маш. ответы дет. Техническое задание (ТЗ) Документ содержащий назначение, технические характеристики и показатели качества, т
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
|
§ 8.6. Расчет прямозубых цилиндрических передач на прочность Расчет на прочность прямозубых и косозубых цилиндрических передач стандартизован ГОСТ 21354—87. В курсе «Детали машин» изучают основы такого расчета. При этом вводят некоторые упрощения, мало влияющие на результаты расчетов для большинства случаев практики. Силы в зацеплении. На рис. 8.17 Fn — нормальная сила, направленная по линии зацепления как общей нормали к рабочим поверхностям зубьев. Силы, действующие в зацеплении, принято прикладывать в полюсе зацепления. При этом силу Fn переносят в полюс и раскладывают на окружную Ft и радиальную Fr. Такое разложение удобно при расчете валов и опор. По заданным Τ и d определяют и через нее выражают все другие составляющие: Расчет прочности зубьев по контактным напряжениям. Исследованиями установлено, что наименьшей контактной усталостью обладает околополюсная зона рабочей поверхности зубьев, где наблюдается однопарное зацепление (см. рис. 8.5). Поэтому расчет контактных напряжений принято выполнять при контакте в полюсе зацепления (рис. 8.18). Контакт зубьев можно рассматривать как контакт двух цилиндров с радиусами pt и р2. При этом контактные напряжения определяют по формуле (8.2), а именно: Для прямозубых передач с учетом формул (8.4)...(8.6) Радиусы кривизны эвольвент зубьев в точке контакта (рис. 8.18) 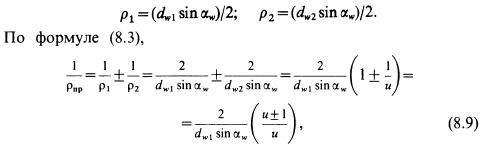 где u = dw2/dwi=z2/zl, знак « + » — для наружного, а « —» — для внутреннего зацепления. Подставляя в формулу (8.7) и заменяя cosawsinaw = = (sin 2ow)/2, получаем Параметр u = z2/zl по ГОСТ 16532—70 называют передаточным числом и определяют как отношение большего числа зубьев к меньшему независимо от того, как передается движение: от ζ ι к ζ2 или от ζ2 к Zj. Это передаточное число и отличается от передаточного отношения /, которое равно отношению угловых скоростей ведущего колеса к ведомому и которое может быть мейьше или больше единицы, положительным или отрицатель¬ным. Применение и вместо i связано только с принятой формой расчетных зависимостей для контактных напряжений [см. вывод формулы (8.9), где рпр выражено через (меньшее колесо), а не через d2 (большее колесо)]. Значение контактных напряжений, так же как и значение передаточного числа м, не зависит от того, какое колесо ведущее, а значение передаточного отношения / зависит.
  В шевронной передаче осевые силы на полушевронах замыкаются на зубчатых колесах и на валы и опоры не передаются В шевронной передаче осевые силы на полушевронах замыкаются на зубчатых колесах и на валы и опоры не передаются
Расчет на контактную прочность Вследствие наклона зубьев в зацеплении одновременно находится несколько пар зубьев, что уменьшает нагрузку на один зуб, повышая его прочность (снижая расчётные напряжения). Аналогично расчету прямозубой передачи межосевое расстояние для косозубых колес определяют по формуле (2.3.17): , где Ка = 43 МПа – для косозубых колес. Контактные напряжения в поверхностном слое зубьев , где - коэффициент нагрузки при расчете по контактным напряжениям; - 1,04 – 1,13 коэффициент нагрузки, учитывающий распределение нагрузки между зубьями и зависит от окружной скорости; - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий); для косозубых передач выбирается с учетом расположения колеса на валу и термообработки; - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки =1,02-1,06 при любой твердости, скорость до 10 м/с, =1,1 при твердости поверхности не больше 350 НВ и скорости 10-20 м/с, =1,05 при твердости более 350 НВ и скорости 10-20 м/с. Косозубые передачи работают более плавно, чем прямозубые, поэтому коэффициент , меньше. Условие контактной прочности косозубой передачи , Если условие не выполняется, то изменяют ширину венца колеса b2, не выходя за пределы рекомендуемых значений . Если это не даст желательного результата, то либо назначает другие материалы колёс или другую термообработку, и расчёт повторяют. Расчет допускаемых напряжений ведется аналогично расчету прямозубых колес 4.5.5 Расчёт зубьев на изгиб Наклонное расположение зубьев увеличивает их прочность на изгиб и уменьшает динамические нагрузки. Это учитывается введением в расчётную формулу прямозубых передач поправочных коэффициентов и . Формула проверочного расчёта косозубых передач (2.3.41), где YF - коэффициент формы зуба выбирают по эквивалентному числу зубьев zv; - коэффициент, учитывающий наклон зуба; - коэффициент распределения нагрузки по ширине венца определяют по аналогии с прямозубыми передачами; = 0,81-0,91 - коэффициент распределения нагрузки между зубьями; - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки =1,2 при твердости зубьев не больше 350НВ, = 1,1 при твердости зубьев более 350 НВ. Нормальный модуль зубьев mn определяют по аналогии с прямозубыми передачами. При некоторых средних значениях коэффициентов получим формулу для приближенного определения модуля косозубых передач (2.3.42), и для шевронных передач (2.3.43), При проверке по формуле (2.3.41): можно получить значительно меньше , что не является недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб.Если расчётное значение превышает допускаемое, то применяют колёса, нарезанные с положительным смещением инструмента, или увеличивают m; > означает, что в передаче из данных материалов решающее значение имеет не контактная прочность, а прочность зубьев на изгиб. На практике к таким передачам относятся передачи с высокой твёрдостью рабочих поверхностей зубьев – 51…63HRCэ (цементация, нитроцементация, азотирование). Проектировочный расчёт таких передач следует выполнять с целью обеспечения прочности зубьев на изгиб по форме определения минимально допустимого модуля m, а затем выполнить проверочный расчёт зубьев на контактную прочность.
Для зубчатых колес со шлифованной переходной поверхностью зубьев ты6 и При Н>350НВ и нешлифованной поверхностью 9 и Рекомендуют принимать NFG = 4-106 для всех сталей. При постоянном режиме нагрузки эквивалентное число циклов NFE находят по формуле (8.60). При переменном режиме нагрузки, по аналогии с формулой (8.63), Здесь учтено, что напряжения изгиба пропорциональны нагруз¬ке. При использовании типовых режимов нагружения (рис. 8.42) где MF —по табл. 8.10; NK — по формуле (8.65). Допускаемые напряжения для проверки прочности зубьев при перегрузках. Кратковременные перегрузки (см., например, момент Тпяк на рис. 8.41), не учтенные при расчете на усталость, могут привести к потере статической прочности зубьев. Поэтому после определения размеров передачи по сопротивлению усталости необходимо проверить статическую прочность при перегрузках. Максимальные контактные напряжения аНтах при перегрузке моментом Гпик можно выразить через известное напряжение σΗ (см. формулу (8.10)]: где σΗ и Гтах— соответственно расчетные напряжения и момент по контактной усталости зубьев; [ая]тах — предельное допуска¬емое напряжение. Если значение Гпик не задано (например, циклограммой на рис. 8.41), его определяют по формуле Гпик = КТт&х, где К— коэффициент внешней динамической нагрузки по табл. 0.1. [ая]тах = 2,8ат при нормализации, улучшении или объемной закалке зубьев (στ — предел текучести материала); [aH]max=40 HRC при цементации, закалке т.в.ч. и азотировании зубьев (см. также табл. 8.9). Аналогично, максимальные напряжения изгиба где aF, Ттах — напряжение и момент при расчете на усталость; [aF]max — предельное допускаемое напряжение. Wmax«0,8ax при Η <350 НВ; [aJmax«0,6aB при Η >350 НВ (σΒ — предел про¬чности материал) (см. также табл. 8.9). § 8.14. Оптимизация конструкции зубчатых передач При изложении содержания настоящей главы мы отмечали влияние различных параметров на габариты (массу), нагрузочную способность и долговечность передачи. В этом параграфе эти сведения обобщаются с позиций оптимизации конструкции.
Передачи, имеющие зубчатые колеса с подвижными осями. Достоинства:
Недостатки:
Расчет планетарной передачи. Подбор чисел зубьев колес. Центральная шестерня а (za) Задают из условия неподрезания ножки зуба: za≥ 17. Принимают: za = 24 при Н ≤ 350 НВ; za = 21 при 45HRC < H ≤ 52HRC za= 17 при Н>52 HRC. Неподвижное центральное колесо b (zb) Определяют по заданному передаточному отношению ubah: 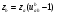 Расчет геометрических параметров для планетарной передачи производят аналогично, как и для цилиндрической передачи
Передачи с зацеплением Новикова В 1954 г. М.Л. Новиковым было разработано зубчатое зацепление с круговым профилем зубьев. К преимуществам передач Новикова относятся повышенная нагрузочная способность и контактная прочность по сравнению с эвольвентной косозубой передачей. Недостатками является чувствительность к изменению межосевого расстояния, сложный исходный контур режущего инструмента; низкая изломная прочность. Принцип зацепления Известно, что прямозубые колеса с круговым профилем зубьев являются несопряженными, и такая передача работать не может. Для сохранения непрерывности зацепления передачи Новикова выполняют косозубими с осевым коэффициентом перекрытия . При вращении колес косые зубья перекатываются в плоскости n-n как цилиндры. Точка контакта a перемещается вдоль зубьев с одного конца ко второму. Линия контакта цилиндров называется полюсной линией. Линия, по которой перемещается точка контакта a , называется линией зацепления. Если линия зацепления расположена за полюсной линией (в направлении вращения ведущего колеса), то зацепление имеет название заполюсное. Если до полюса - дополюсное. Одна и та же пара колес может иметь заполюсное и дополюсне зацепление в зависимости от того, какое колесо является ведущим. Признаком заполюсного зацепления является выпуклый профиль ведущего зуба и вогнутый ведомого. Дополюсного - вогнутый профиль ведущего и выпуклый ведомого. Очевидно, возможно выполнять колеса таким образом, чтобы одна часть профиля будет выпуклой, а вторая - вогнутой. Такие колеса смогут входить в зацепление и за полюсом, и до полюса, такое зацепление называется дозаполюсним. Дозаполюсне зацепление имеет две линии зацепления, соответственно в два раза больше и число точек контакта зубьев. В таких передачах зубья шестерни и колеса имеют одинаковый профиль: выпуклый возле головки и вогнутый возле ножки. Колеса передач Новикова выполняются из тех же материалов, что и эвольвентные колеса, чаще всего обрабатываются до твердости. Для нарезания зубьев шестерни и колеса используется тот же инструмент. Колеса Новикова нарезают, как правило, без смещения. Основные геометрические параметры Угол наклонения зубьев в передачах Новикова принимается Расчет на прочность Без учета деформаций и приработки колес контакт зубьев в передачах Новикова происходит в точке. Однако малая разность радиусов кривизны выпуклых и вогнутых поверхностей и большие радиусы кривизны косых зубьев приводит к тому, что контакт в точке становится контактом по пятну. В дозаполюсному зацеплении будет два пятна контакта. Контакт в точке способствует потому, что колеса Новикова менее чувствительные к перекосам, но более чувствительные к изменению межосевого расстояния, а также приводит к снижению изломной прочности. Основным критерием работоспособности и расчета передач Новикова есть прочность по контактным напряжениям и напряжением изгиба. Средства повышения прочности:
В передачах Новикова условия контакта зубьев значительно отличаются от условий контакта по Герцу. Размеры площади пятна контакта соответствуют размеру зубьев, а контактные напряжения близки к напряжениям смятия. Поэтому расчет передач Новикова по контактным напряжениям, определяемым зависимостями Герца, условный. Дозаполюсне зацепление преимущественно:
Основные геометрические параметры. Колеса Новикова нарезают как правило без смещения. Материалы Те же самые, что и для эвольвентных передач, наиболее распространенные с <350HB.
Механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей и моментов. В этих передачах, так же как и в конических, оси валов рас полагаются под углом, но не пересекаются, а перекрещиваются, т. е. проходят на некотором расстоянииа друг от друга Перекрестное расположение осей придает этим передачам некоторые особенности, которые используют на практике. Напри мер, подшипники обоих валов можно располагать по обе стороны колеса; оба вала могут продолжаться в обе стороны от колеса, что позволяет передавать движение от одного ведущего вала несколь ким ведомым.Основными недостатками передач с перекрещивающимися осями являются повышенное скольжение в зацеплении и связанные с этим повышенный износ и склонность к заеданию. Винтовые и гипоидные передачи применяют преимущественно в специальных изделиях. Поэтому в курсе деталей машин дается только общее понятие об этих передачах. Винтовая передача осуществляется цилиндрически ми косозубыми колесами. При перекрестном расположении осей валов начальные цилиндры колес соприкасаются в точке, поэтому зубья имеют точечный контакт. Векторы окружных скоростей колес направлены под углом перекрещивания, поэтому в зацеплении на блюдается большое скольжение. Точечный контакт и скольжение приводят к быстрому износу и заеданию даже при сравнительно небольших нагрузках. Поэтому винтовые передачи применяют главным образом в кинематических цепях приборов. В силовых передачах их заменяют червячными передачами с многозаходными червяками. Во многих случаях такая замена целесообразна и в пе редачах приборов. Гипоидная передача осуществляется коническими коле сами с косыми или криволинейными зубьями. Вершины конусов колес не совпадают. Угол перекрещивания осей чаще всего выпол няется равным 90°. В отличие от винтовых передач гипоидные могут быть выполнены с линейным контактом зубьев. Скорости скольжения в гипоидных передачах меньше, чем в винтовых. Поэто му они обладают повышенной нагрузочной способностью. На прак тике опасность заедания, связанная со скольжением, устраняется применением специальных смазочных материалов с антизадирными присадками (гипоидные масла) и термообработкой зубьев до высо кой твердости, а также ограничением смещенияа осей валов.
Недостатком гипоидных передач являются повышенные требо вания к точности изготовления и монтажа. Гипоидные передачи применяют главным образом в автотракторном и текстильном машиностроении. Размещение карданного вала ниже оси ведущих колес автомобиля позволяет понизить центр тяжести автомобиля и тем самым повысить его устойчивость. Применение гипоидной передачи в прядильных машинах позволяет передавать движение от одного вала многим десяткам веретен. Расчет гипоидных передач излагается в специальной литературе Оси перекрещиваются (червячная передача)
Геометрические параметры и изготовление червячных передач В червячной передаче, как и в зубчатой, различают диаметры начальных (dw1, dw2) и делительных (d1, d2) цилиндров. В передачах без смещения . Червяки различают: 1. по форме образующей поверхности:
2. по форме профиля витков:
Червячное колесо нарезают червячными фрезами. Основные геометрические параметры червяка и колеса: профильный угол;
Кинематические параметры червячной передачи В червячной передаче, в отличии от зубчатой, окружные скорости и не совпадают. Они направлены под углом 900 и отличаются по значению. При относительном движении начальные цилиндры скользят. При одном обороте червяка колесо поворачивается на угол, охватывающий число зубьев колеса, равное числу заходов червяка. Основным преимуществом червячной передачи является большие передаточные отношения: в силовых передачах 10...80 , в кинематических передачах до 300 . При движении витки червяка скользят по зубьям колеса, как в винтовой паре. Скорость скольжения направлена по касательной к винтовой линии червяка Большое скольжение является причиной снижения ККД, повышенного износа и заедания ККД червячной передачи ККД повышается в случае увеличения числа заходов червяка и снижается с уменьшением коэффициента трения или угла трения. Коэффициент трения снижается с увеличением скорости скольжения . Кроме того, значение коэффициента трения зависит от шероховатости поверхности трения, а также качества смазочного масла. Свойство самоторможения применяется в грузоподъемных механизмах. ККД самотормозящей пары, как правило, меньше 0,5. Силы в зацеплении
КПД закрытой червячной передачи должен учитывать потери в за цеплении и подшипниках, а также потери на разбрызгивание, перемешиваниемасла и др.Роль смазывания в червячной передаче еще важнее, чем в зубчатой, так как в зацеплении происходит скольжение витков червяка вдоль кон тактных линий зубьев червячного колеса. В случае несовершенства сма зывания резко возрастают потери, возможно повреждение зубьев. Червячная передача является зубчато-винтовой и имеет потери, свой ственные как зубчатой передаче, так и передаче винт — гайка. Среднее значение КПД при однозаходном червяке можно принимать равным 0,7 - 0,75; при двухзаходном 0,75 - 0,82; трех- и четырехзаходном 0,83 -0,92. Общий КПД для закрытой червячной передачи можно опреде лить по формуле (уточненный расчет) где степень п— число пар подшипников; Значения угла
Силы в зацеплении определяют для случая контакта рабочих поверхностей в полюсе зацепления и раскладывают по трем взаимно перпендикулярным осям. Окружная сила на колесе равна по модулю осевой силе на червяке: Окружная сила на червяке равна осевой силе на колесе: Радиальная сила, раздвигающая червяк и колесо: В этих зависимостях T2 и T1 – вращающие моменты на валах колеса и червяка, α – угол профиля витка червяка, d2 – делительный диаметр колеса, dw1 – начальный диаметр червяка.
По контактным напряжениям 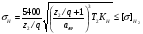 Т2 – крутящий момент на валу колеса, Н·м; αω– межосевое расстояние передачи, мм; [σ]H2 – допускаемое контактное напряжение материала червячного колеса, МПа; KH – коэффициент нагрузки: 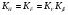 KV – динамический коэффициент; Kβ - коэффициент неравномерности распределения нагрузки по длине контактной линии. По напряжениям изгиба 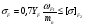 Рассчитывают только зубья колеса, т.к. витки червяка по форме и материалу значительно прочнее зубьев колеса. Расчет является приближенным, т.к. зуб колеса имеет переменную форму сечения по ширине колеса и основание его расположено не по прямой линии, а по дуге окружности. Рассчитывают только зубья колеса, т.к. витки червяка по форме и материалу значительно прочнее зубьев колеса. Расчет является приближенным, т.к. зуб колеса имеет переменную форму сечения по ширине колеса и основание его расположено не по прямой линии, а по дуге окружности.[σ]F2 – допускаемое изгибное напряжение для материала колеса; ωFt – удельная расчетная окружная сила 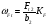 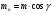 mn – нормальный модуль зацепления; mn – нормальный модуль зацепления; 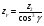 YF– коэффициент формы зуба (его находят по эквивалентному числу зубьев): YF– коэффициент формы зуба (его находят по эквивалентному числу зубьев):
Червяк: Среднеуглеродистые сталей марок 45, 50, легированных 40Х, 40ХН с поверхностной или объемной закалкой до твердости 45…54 НRC и последующим шлифованием витков. Цементуемые стали 18ХГТ, 20Х с твердостью после закалки 56 …63 НRC. Зубчатые венцы червячных колес: По мере убывания антизадирных и антифрикционных свойств и рекомендуемым для применения скоростям скольжения:
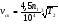 Для выбора материала колеса предварительно определяют ожидаемую скорость скольжения, м/с: Для выбора материала колеса предварительно определяют ожидаемую скорость скольжения, м/с: Допускаемые контактные напряжения: 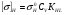 для оловянных бронз – определяют из условия сопротивления усталостному выкрашиванию рабочих поверхностей зубьев для оловянных бронз – определяют из условия сопротивления усталостному выкрашиванию рабочих поверхностей зубьев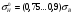 σНо – предел контактной выносливости при числе циклов перемены напряжений 107, МПа; Сv – коэффициент, учитывающий интенсивность изнашивания зуба колеса в зависимости от скорости скольжения; КНL – коэффициент долговечности. σНо – предел контактной выносливости при числе циклов перемены напряжений 107, МПа; Сv – коэффициент, учитывающий интенсивность изнашивания зуба колеса в зависимости от скорости скольжения; КНL – коэффициент долговечности. σВ – временное сопротивление для бронзы на растяжение, МПа для твердых бронз (алюминиево-железистых) и чугунов – принимают из условия сопротивления заеданию либо по эмпирическим формулам, либо численно в зависимости от скорости скольжения
Их применяют в паре с твердыми (>45 HRC) шлифованными и полированными червяками для передач, у которых м/с. Чугун серый или модифицированный применяют при 2 м/с, преимущественно в ручных приводах. Допускаемые контактные напряжения для оловянных бронз: [ Vs;m/C... <1 2 3 4 5 6 7 ^8 С0 1,33 1,21 1,11 1,02 0,95 0,88 0,83 0,8 При проектном расчете скорость скольжения (м/с) оцени¬вают по приближенной зависимости Приведенные зависимости относятся к длительному сроку службы при нагрузке, близкой к постоянной. Допускаемые напряжения изгиба для всех марок бронз Для проверки червячных передач на прочность при кратковременных перегрузках, которые не учитывают в основном расчете, принимают следующие предельные допускаемые напряжения: оловянные бронзы |
