Технология молока и молочных продуктов

• Название: Технология молока и молочных продуктов
• Анкор: Технология молока и молочных продуктов.doc
• Дата: 28.01.2017
• Размер: 3.66 Mb.
• Имя файла: Технология молока и молочных продуктов.doc
• Тип: Учебник; #380
• страница: 48 из 49

МОЛОЧНЫЕ КОНСЕРВЫ

При выработке молочных консервов в нормализованном молоке отношение между жиром и сухим обезжиренным остатком Ж_н.м/ СОМО_н.мдолжно быть таким, чтобы обеспечить стандартное отношение этих частей молока в готовом продукте.

В цельном молоке отношение Ж_м / СОМО_м колеблется от 0,39 до 0,69, а в сухих и сгущенных молочных продуктах Ж_г / СОМО_г – от 3,3 до 0,193. Таким образом, в производстве молочных консервов необходимо изменять соотношение между жиром и сухим обезжиренным остатком в молоке от 0,39–0,69 до 3,3–0,193.

Кроме того, следует учитывать непропорциональность относительных потерь жира и сухого вещества, которая обозначается коэффициентом К.

Если Ж_м / СОМО_м = (Ж_г / СОМО_г) ∙К, то молоко не требует нормализации.

Если Ж_м / СОМО_м < (Ж_г / СОМО_г) ∙К, то при нормализации молока используют сливки.

Обозначим Ж_г / СОМО_г = О_пр, массу сливок найдем по формуле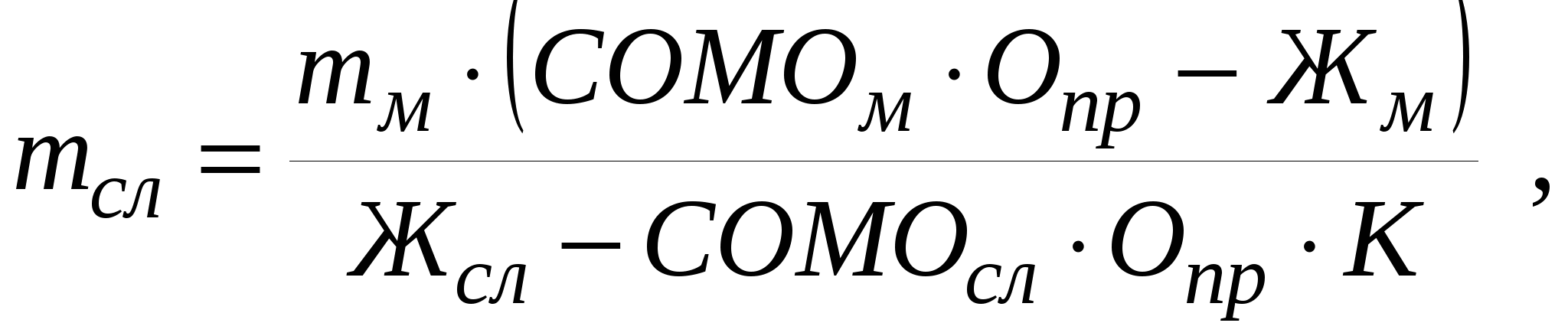

где СОМО_сл – массовая доля сухого обезжиренного молочного остатка в сливках, %.

Массу нормализованного молока определяют как m_н.м=m_м+m_сл.

Массовую долю жира в нормализованном молоке определяют по формуле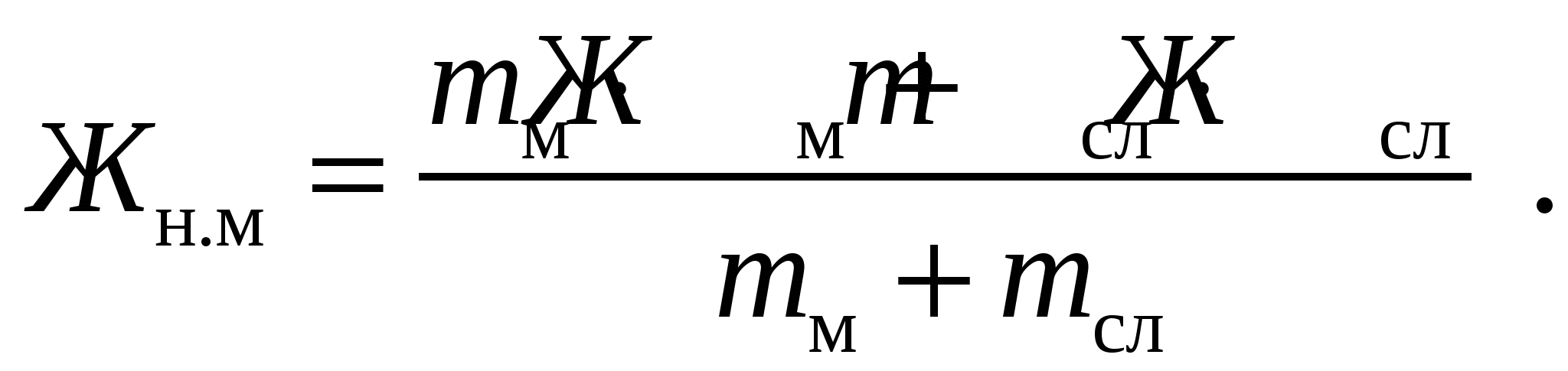



Если Ж_м / СОМО_м> (Ж_г / СОМО_г)∙К, то для нормализации используют обезжиренное молоко или пахту.

Массу обезжиренного молока и пахты определяют по формулам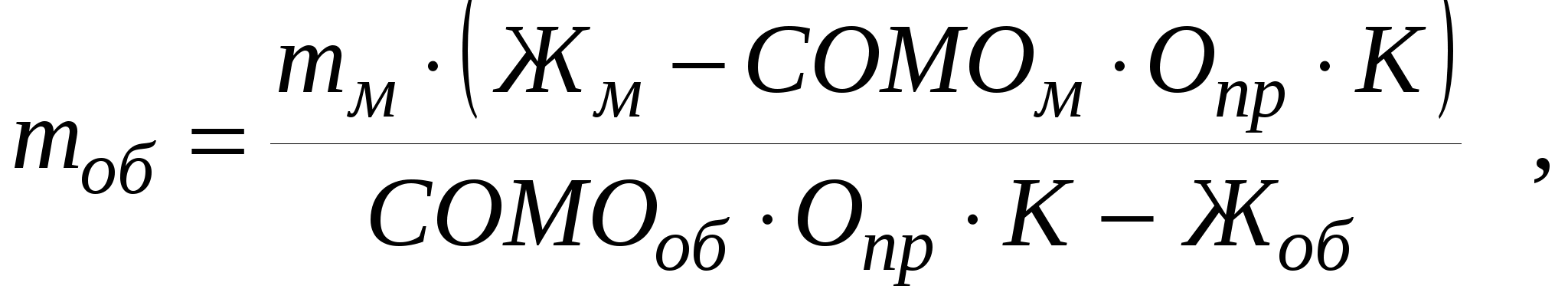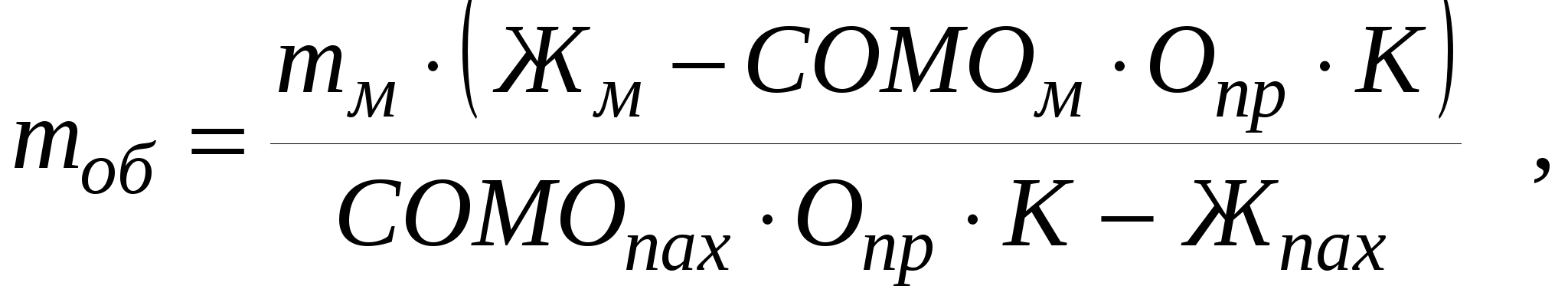



где СОМО_об и СОМО_пах – массовая доля сухого обезжиренного молочного остатка соответственно в обезжиренном молоке и пахте, %.

Тогда т_н.м = т_м +т_об, или m_{н м} = m_м + m_пах

Для группы молочных консервов, в которых нормировано содержание сахарозы, массу сахара можно рассчитать по формулам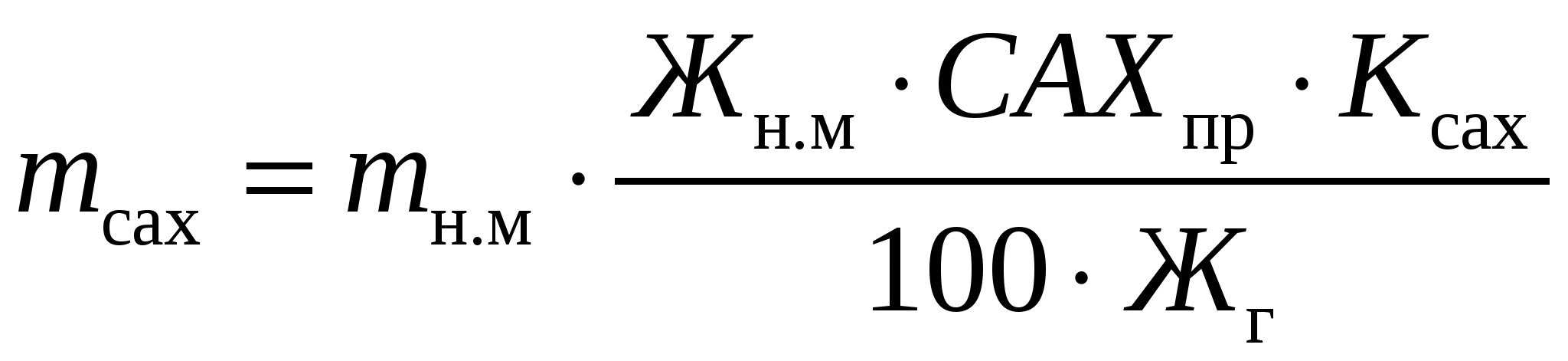



или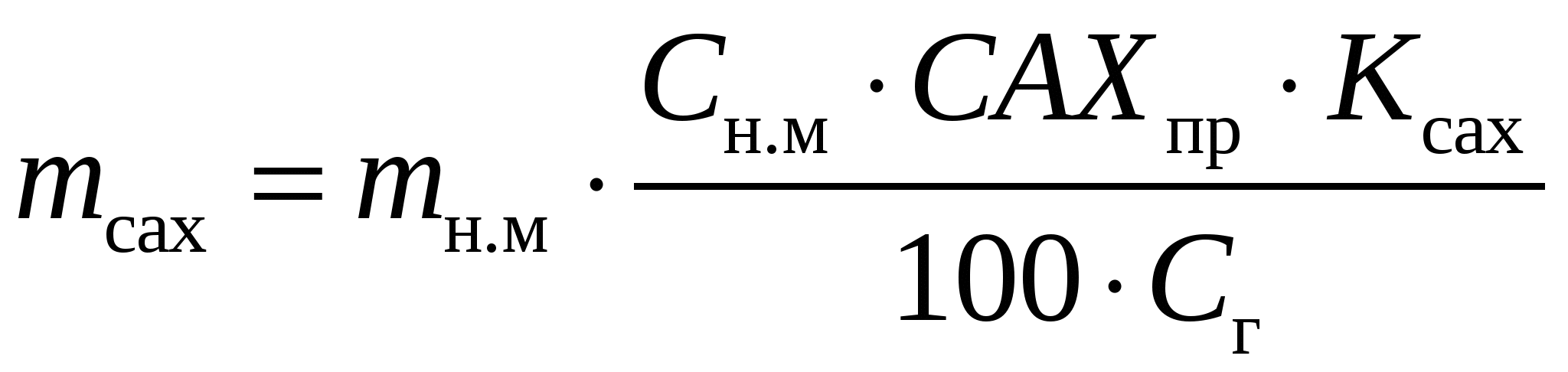



где САХ_пр – массовая доля сахара в продукте, %, K_сах – коэффициент, учитывающий потери сахара; С_н.м и С_г– массовая доля сухого молочного остатка соответственно в нормализованном молоке и продукте, %.

Аналогично можно рассчитать массу любого наполнителя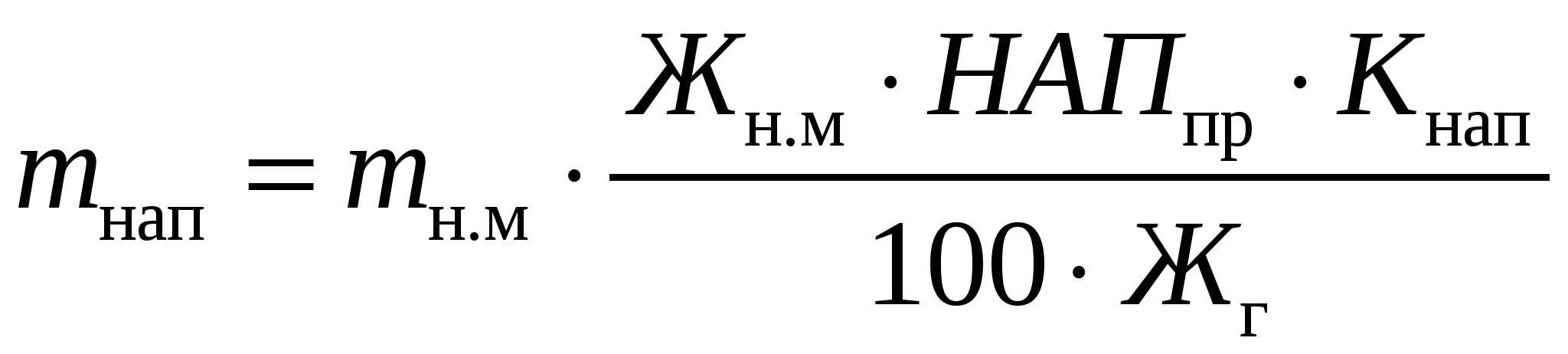



или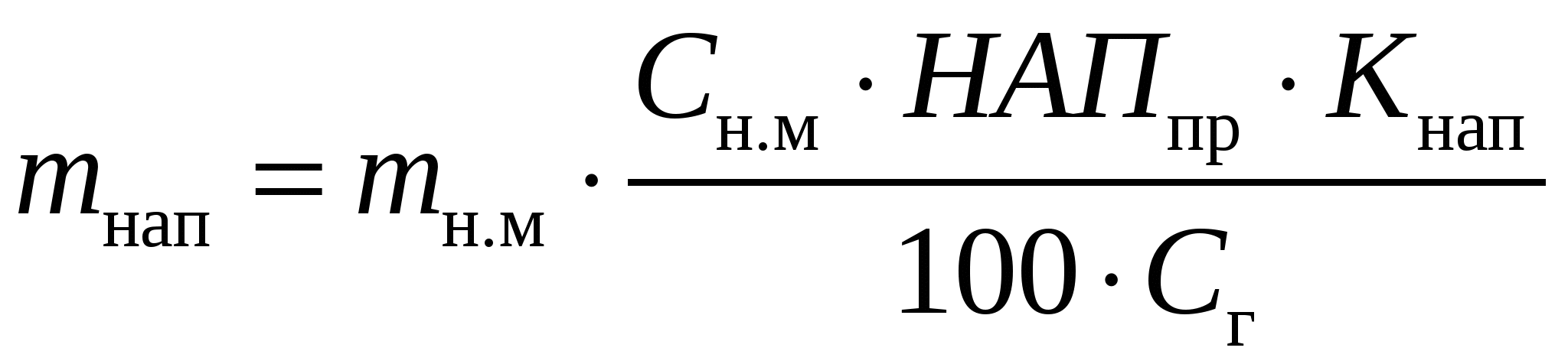



где НАП_пр – массовая доля наполнителя в продукте, %; К_нап – коэффициент, учитывающий потери наполнителя..

РАСЧЕТ РЕЦЕПТУР В ПРОИЗВОДСТВЕ ПРОДУКТОВ СО СЛОЖНЫМ СЫРЬЕВЫМ СОСТАВОМ

В производстве продуктов со сложным компонентным составом рассчитывается рецептура на составление смеси, исходя из состава сырья и готового продукта.

Алгебраический метод расчета. При расчете рецептур составляют столько уравнений, сколько неизвестных видов сырья. Первое уравнение составляется по массе готового продукта и сырья, а остальные – по балансу составных частей.

Выбирая неизвестные виды сырья, необходимо для получения баланса по какому-либо компоненту придерживаться следующего правила: один из неизвестных видов сырья должен содержать этого компонента меньше, а другой больше, чем в готовом продукте, иначе могут быть получены отрицательные значения массы неизвестных видов сырья. Расчет ведут обычно на 100 или 1000 кг готового продукта.

Пусть m₁, m₂, m₃ – неизвестные массы первого, второго и третьего видов сырья, кг;

Ж₁, Ж₂, Ж₃ –массовая доля жира в соответствующих видах сырья, %;

О₁, О₂, О₃ – массовая доля сухого обезжиренного остатка в соответствующих видах сырья, %;

Ж_см и О_см – соответственно массовая доля жира и сухого обезжиренного остатка в смеси, %;

 m_и – сумма масс известных видов сырья, кг;

 m_и ∙Ж_и – суммарная масса жира в известных видах сырья, кг;

 m_и ∙О_и – суммарная масса сухого обезжиренного остатка в известных видах сырья, кг.

Сначала составляют материальный баланс по общей массе смеси (m_см = 100 кг)

.

Затем составляют баланс по жиру



и баланс по сухому обезжиренному остатку

.

Решая эти уравнения совместно, находят m₁, m₂, m₃.

Пример. Составить 100 кг смеси сливочного мороженого с массовой долей жира 10%, СОМО – 10%, сахара – 16%, агара – 0,3%.

Для приготовления смеси имеется следующее сырье:

– молоко коровье жирностью 3,5%, СОМО – 9%;

– сливки жирностью 35%, СОМО – 7,2%;

– молоко сгущенное с сахаром с массовой долей жира 8,5%; СОМО – 20%, сахара – 43,5%.

Расчет. Предварительно определяют количество смеси за вычетом сахара и агара

100 – (16 + 0,3) = 83,7 кг.

Обозначим требуемую массу молока m₁, массу сливок m₂, а массу сгущенного молока с сахаром m₃.

Для решения задачи с тремя неизвестными составим три уравнения

– общий баланс: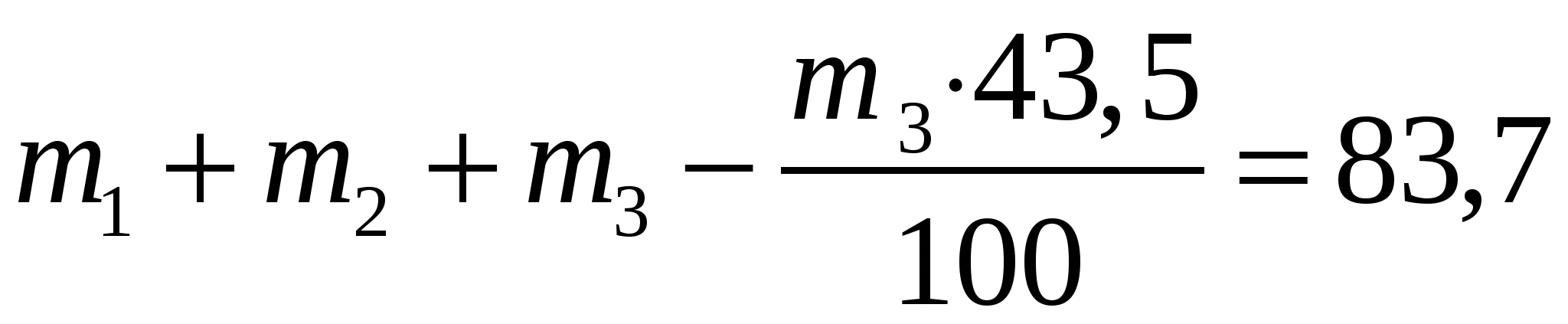

;

– баланс по жиру:

;

– баланс по СОМО:

.

Решая совместно эти три уравнения, находим массу молока, равную 37,3 кг, массу сливок 34,7 кг и массу молока сгущенного с сахаром 20,7 кг. Далее рассчитываем недостающую массу сахара. В 100 кг смеси мороженого должно содержаться 16 кг сахара. В рассчитанном количестве сгущенного молока с сахаром содержится сахара (20,7^. 43,5) / 100 = 9,0 кг.

Следовательно, недостающее количество сахара составляет

16,0 – 9,0 = 7,0 кг.

Результаты расчетов записывают в табл. и подсчитываем количество жира и СОМО в каждом из продуктов.

Таблица

Сырье	Масса сырья, кг	Масса, кг
		Жира	СОМО	сахара
1. Молоко	37,3	1,30	3,36	–
2. Сливки	34,7	6,94	2,50	–
3. Молоко сгущенное с сахаром	20,7	1,76	4,14	9,0
4. Сахар свекловичный	7,0	–	–	7,0
5. Агар	0,3	–	–	–
ИТОГО:	100,0	10,0	10,0	16,0
%	100	10	10	16

Экономико-математический метод расчета рецептур продуктов со сложным компонентным составом основан на решении основной задачи линейного программирования, т.е. системы уравнений и неравенств (их принято называть ограничениями), поиск решения которой выполняется исходя из требования минимизации целевой функции, являющейся линейной формой арифметического вектора, представляющего собой совокупность массовых долей компонентов рецептуры. Как правило, целевая функция несет смысловую нагрузку какого-либо технико-экономического показателя рецептуры, например, ее стоимости. Математическая запись системы ограничений и целевой функции имеет следующий вид.
Целевая функция (стоимость рецептуры)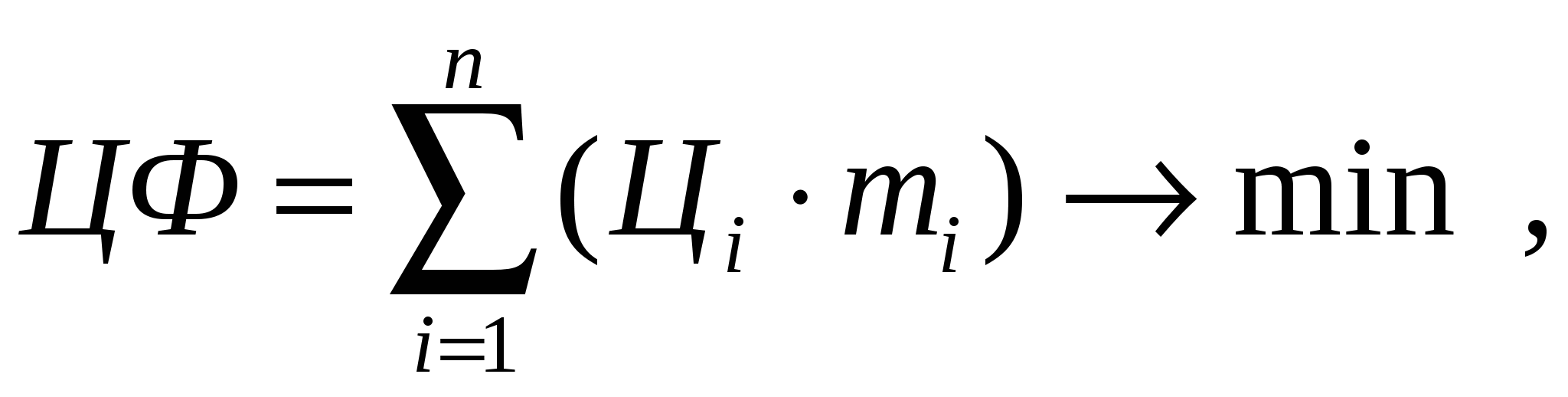

(20)
где Ц_i, m_i – цена (стоимость) единицы массы (руб/кг) и масса i-го компонента (кг), входящего в смесь; n – количество компонентов смеси.

Система ограничений состоит из следующих групп:

– материальный баланс по общей массе и составным частям смеси, массовые доли которых в готовом продукте регламентированы нормативной технической документацией. Это ограничения типа «уравнение»;

– индивидуальные двусторонние ограничения по каждой переменной. Это ограничения типа «неравенство».

Материальный баланс.

а) материальный баланс по общей массе смеси: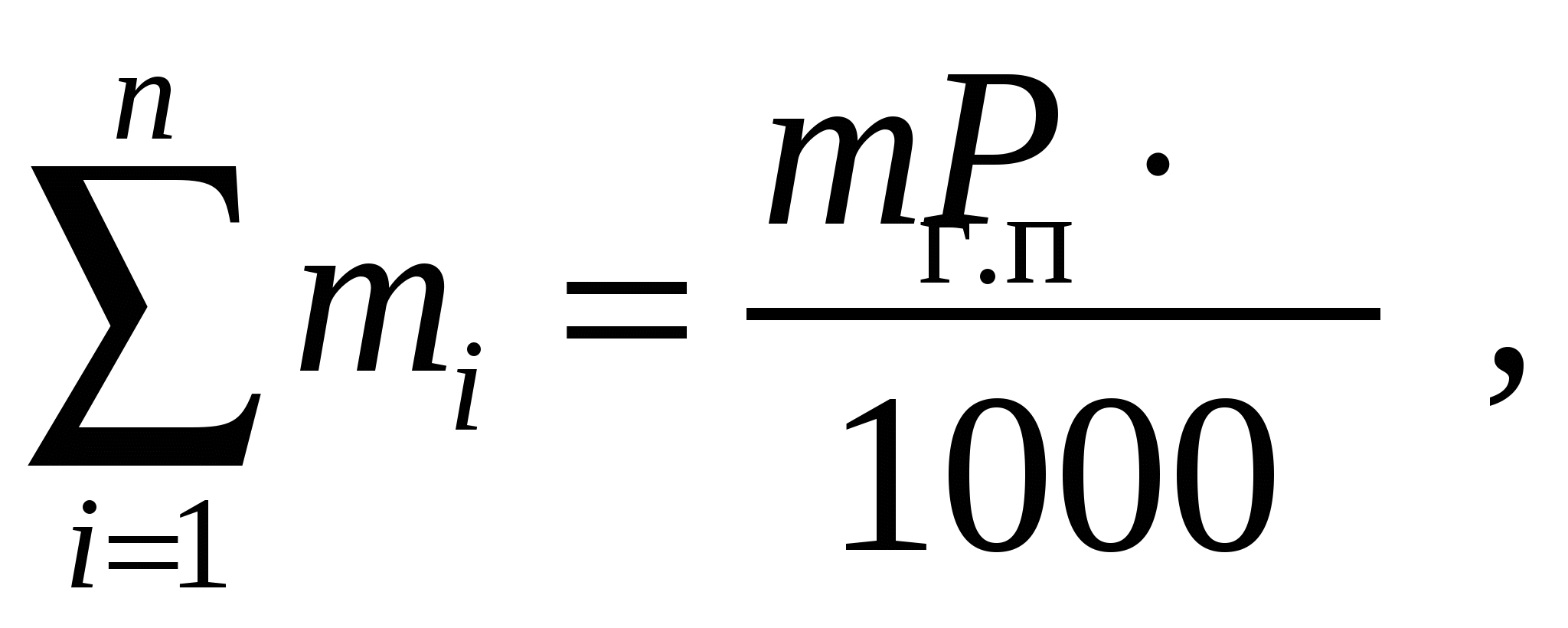
(21)

где m_i – масса i-го компонента смеси, кг; m_г.п – масса готового продукта, кг; P – нормативный расход смеси на 1т готового продукта, кг; n – количество компонентов смеси.

б) материальный баланс по составным частям: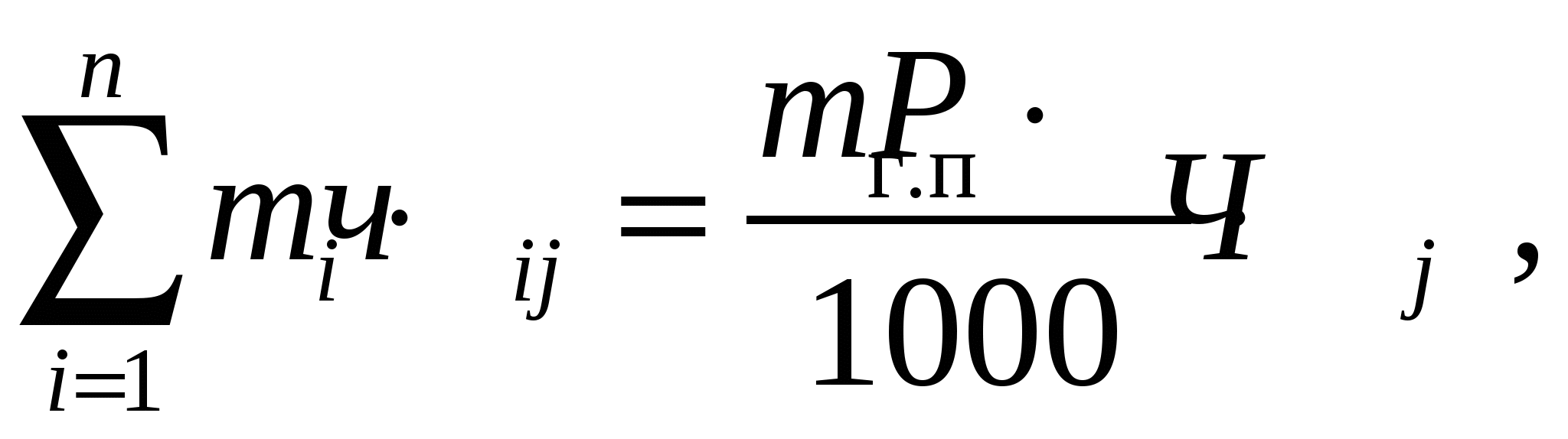
(22)
где m_i – масса i-го компонента смеси, кг; ч_ij – массовая доля j-ой составной части в i-ом компоненте смеси, %; Ч_j– массовая доля j-ой составной части в смеси (готовом продукте), %; m_г.п – масса готового продукта, кг; P – нормативный расход смеси на 1т готового продукта, кг; n – количество компонентов смеси.

Обычно в эту группу входят материальный баланс по жиру, влаге, со содержанию сахарозы, ванилина, наполнителей, стабилизаторов и т.п. В этой группе должны быть только линейно-независимые ограничения, поэтому нет необходимости составлять баланс по СОМО или сухим веществам молока, если ограничения по жиру и влаге уже составлены. Кроме неоправданного увеличения размерности системы ограничений, это может привести к внутренней противоречивости при расчете за счет ошибок округления и, как следствие – к получению недопустимого решения.

Индивидуальные двусторонние ограничения.

Каждое из этих ограничений записываются в виде двойного неравенства.

(23)

где m_i– масса i-го компонента смеси, кг; m_i^min – минимальный объем использования i-го компонента, кг; m_i^max– максимальный объем использования i-го компонента, кг. Такие ограничения необходимы чаще всего для учета наличия ресурсов компонентов. Кроме того, с помощью этих ограничений можно управлять расходом компонентов при составлении смеси.

Совокупность соотношений (20)–(23) образует математическую запись задачи расчета рецептуры продукта со сложным компонентным составом. Решение задачи сводится к нахождению набора неотрицательных значений масс компонентов смеси m_i, удовлетворяющего условиям (20)–(23). Для решения таких задач используется симплекс-метод. Целесообразно выполнять такие расчеты с помощью программы для персонального компьютера. Одним из наиболее популярных инструментов для решения задач оптимизации является надстройка «Поиск решения» процессора электронных таблиц «MS Excel». Эта надстройка позволяет эффективно и быстро находить решения подобных задач, а внутренняя логика электронных таблиц обеспечивает представление задачи в удобной для восприятия табличной форме и упрощает процесс ввода данных.

Таблица исходных данных

№ п/п	Наименование сырья	Ресурс, кг	Цена, руб	Массовая доля, %
				Жира	Влаги	Хлорида натрия	Соли-плавителя
1.	Сыр сычужный крупный	100	100,00	29	42	2	0
2.	Сыр сычужный мелкий	250	90,00	25,2	44	3	0
3.	Сыр свежий Несолёный	1000	80,00	24,75	45	0	0
4.	Молоко сухое обезжиренное	100	65,00	0	4	0	0
5.	Сливки	300	80,00	35	58,9	0	0
6.	Масло Крестьянское	100	120,00	72,5	25	0	0
7.	Поваренная соль	100	2,00	0	0	100	0
8.	Соль-плавитель (раствор)	200	150,00	0	80	0	20
9.	Вода	1000	0,50	0	100	0	0

* Примечание: приведены условные цены на сырье.

Пример. Рассчитать состав смеси для производства 200 кг плавленого сыра с массовой долей жира в сухом веществе 60%, влаги – 52%, хлорида натрия – 1,8 %, соли-плавителя – 2%. Норма расхода смеси на 1 т плавленого сыра составляет 1020 кг. Перечень и химический состав компонентов для составления смеси приведен в табл. . При этом в составе смеси должно быть не менее 10 % сычужных сыров (крупных и мелких).

Расчет. Предварительно рассчитаем абсолютную массовую долю жира в плавленом сыре (смеси).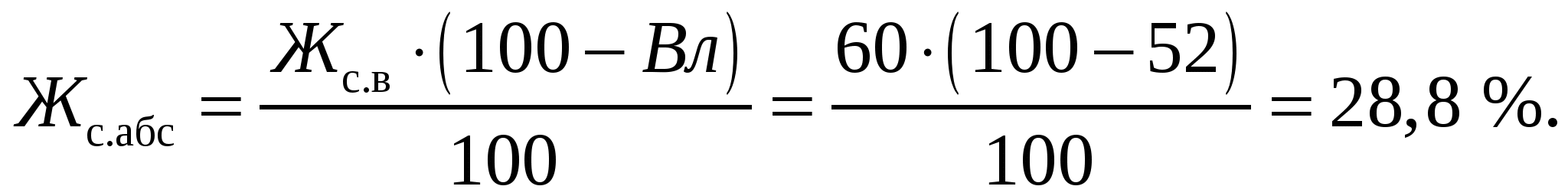



Масса смеси для производства 200 кг плавленого сыра с учетом нормы расхода 1020 кг/т составит 204 кг. Для выполнения условий расчета примем, что сычужных сыров крупных в смеси должно быть не менее 5% , т.е 10,2 кг, мелких – не менее 5 %, т.е 10,2 кг.

Обозначим неизвестные массы компонентов смеси: m₁ – масса сыра сычужного крупного , m₂ – масса сыра сычужного мелкого, m₃ – масса сыра свежего несоленого, m₄ – масса сухого обезжиренного молока, m₅ – масса сливок, m₆ – масса масла, m₇ – масса поваренной соли, m₈ – масса раствора соли-стабилизатора , m₉ – масса воды.

Целевая функция (стоимость смеси) :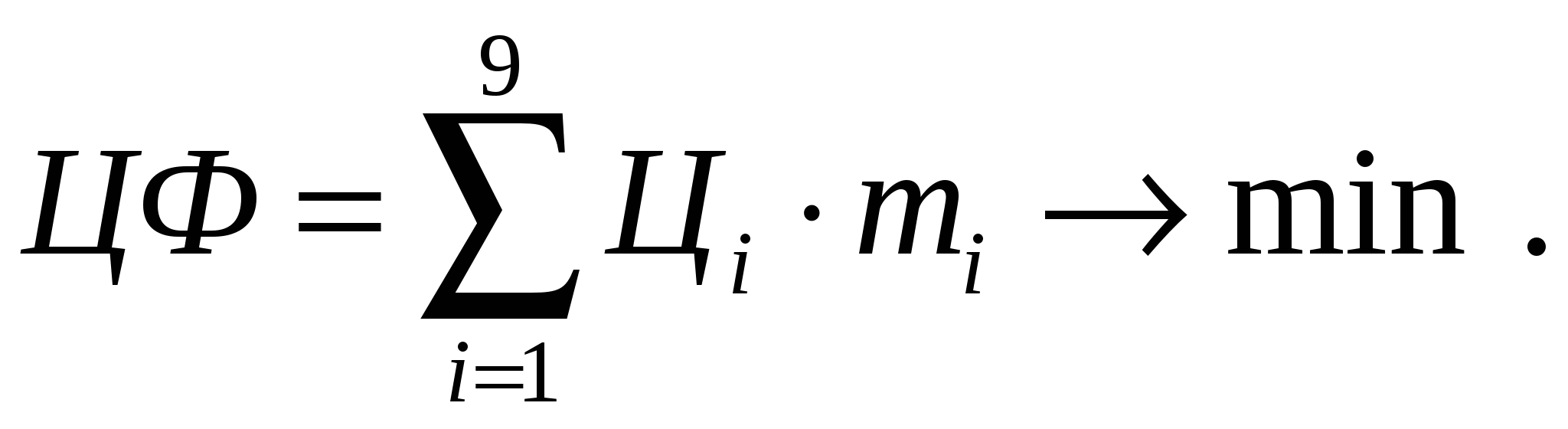



Ограничения материального баланса:

– по общей массе смеси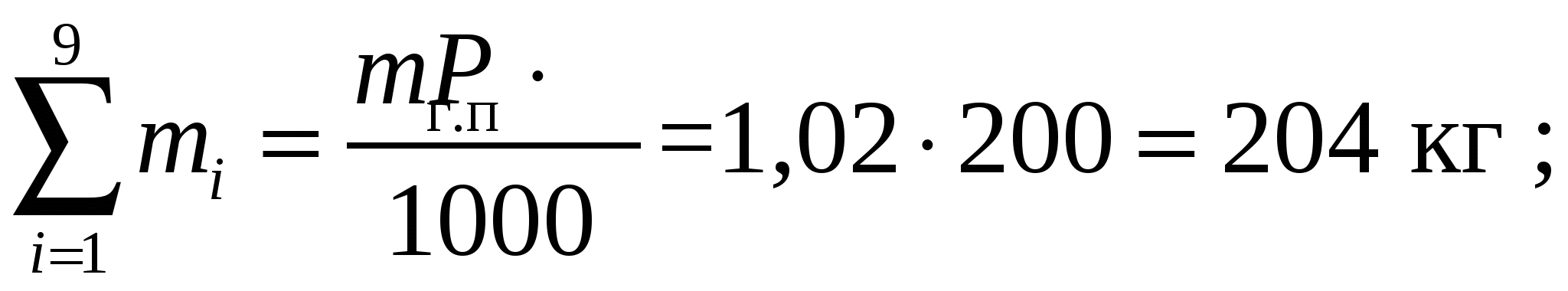



– материальный баланс по жиру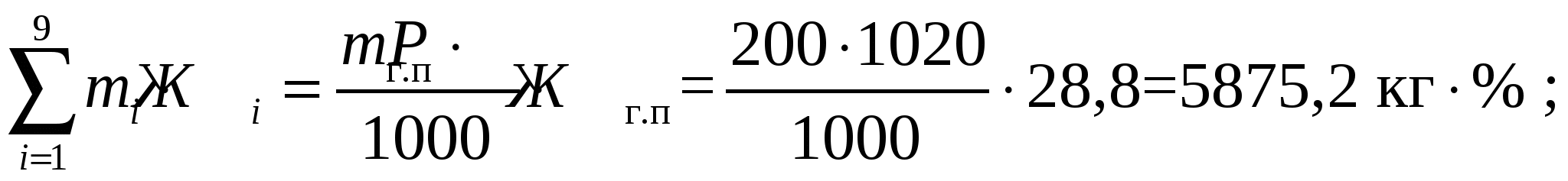



– материальный баланс по влаге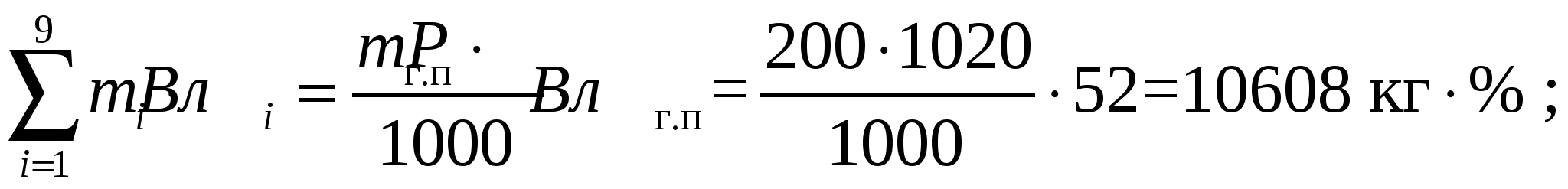



– материальный баланс по хлориду натрия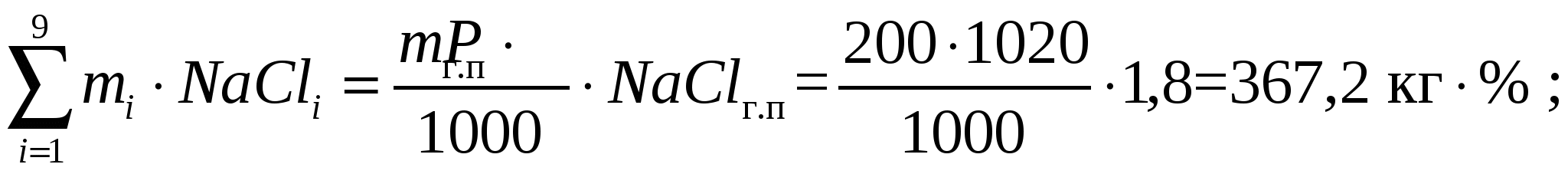



– материальный баланс по соли-плавителю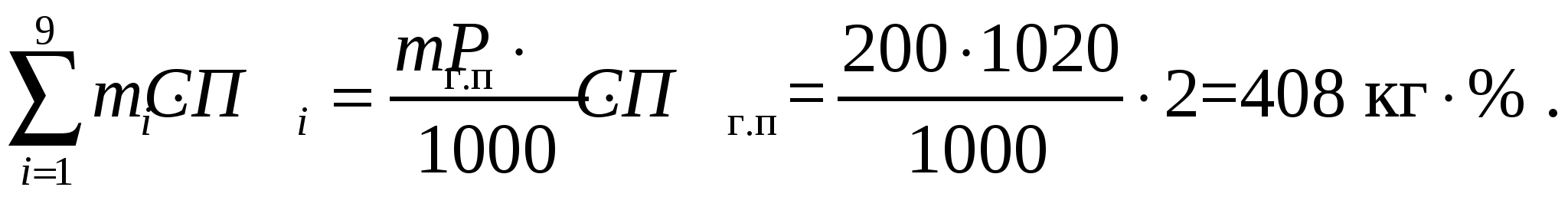



Индивидуальные двусторонние ограничения.

В соответствии с данными табл. индивидуальные ограничения можно записать следующим образом



Для нахождения решения задачи воспользуемся процессором электронных таблиц «MS Excel» и его надстройкой «Поиск решения» (в англоязычном варианте «Solver»). Перенесем данные из табл. На рабочий лист Excel’а, дополнив ее колонкой для записи решения задачи (Рис. ).

В верхнюю таблицу на рабочем листе добавим также колонку с информацией о минимальном использовании сырья. Ниже на листе разместим формулу для расчета значения целевой функции и общей массы смеси. В нижней таблице расположим информацию об ограничениях материального баланса. Во вторую колонку нижней таблицы введем формулы для расчета левых частей ограничений материального баланса, а в третью – для правых частей. В четвертой колонке расположим данные о требованиях стандарта к составу готового продукта и смеси.

Изначально в правой колонке верхней таблицы находятся нули. Начальные значение целевой функции и общей массы смеси также равны нулю.

Установив указатель активной ячейки в поле со значением целевой функции, запускаем «Поиск решения». При этом на экране появляется диалоговое окно, с помощью которого вводим адреса ячеек с искомыми переменными m₁ – m₉, ячейки, содержащей формулу для расчета целевой функции, а также ячеек правых и левых частей ограничений материального баланса и двусторонних индивидуальных ограничений.

По окончании ввода запускаем расчет и в случае получения допустимого решения на экране будут отображены результаты расчета значений m₁ – m₉ и значение целевой функции. На рис. эти числовые значения выделены более крупным и полужирным шрифтом.

Использование надстройки «Поиск решения» позволяет быстро выполнять большой объем вычислений. При этом возможно моделирование различных ситуаций, связанных с изменением ресурсов сырья, его стоимости и других условий расчета.