Рииии. Тема 1 Статистика. Организация и этапы статистического исследования
 Скачать 6.04 Mb. Скачать 6.04 Mb.
|
|
Тема 5: Стандартизация-это метод расчёта условных показателей, принимающих интенсивные или средние величины, когда сравнение последних затруднено из-за несопостовимости состава сравниваемых групп. Статистический метод-это статистический метод, позволяющий исключить влияние неодинакового состава сравниваемых групп на общие показатели. Примеры применения стандартизации-показатели заболеваемости, смертности между больницами, городами, регионами. Методы стандартизации: Прямой, когда известно явление и среда Косвенный, когда известна среда Обратный, когда известно явление 1.Прямой метод - известно явление и среда. Вычисляем показатель летальности (ИП) Сравниваем получившиеся показатели летальности Показатель летальности по отдельной больницы А< больницы Б(9<12), а в целом по больницам получается обратная картина(6,7> 5,8) Расчёт стандартизированных показателей (прямой метод)
Это логическое несоответствие связано с разнородным состоянием больных по отделениям отдельных больных, для того, чтобы исключить влияние неодинакового состояния больных по отделениям больниц А и Б применяют стандартизацию. 1 способ Прямой метод Суть прямого метода состоит в вычислении общих интенсивных показателей в одинаковых признаках (единиц наблюдения), совокупностях; для чего рассчитывают частные показатели в сравниваемых группах, по которым судят об их истинном соотношении в исследуемых совокупностях; предполагают, что сравниваемые совокупности одинаковы, т.е. стандартны по составу. Метод применяется при сравнении общих интенсивных показателей здоровья различных по составу (по полу, возрасту и другим признакам) групп населения. Суть метода состоит в исключении влияния на общий показатель разного состава совокупностей по одному, двум признакам или более. За стандарт принимают средний состав обеих групп, одну из сравниваемых групп или какую-то третью группу, близкую к сравниваемым. Рассчитывают условные величины в каждой группе стандарта и общие стандартизированные показатели, которые тоже являются условными. Если соотношение стандартизированных показателей получается иное, чем реальных, то делают вывод о том, что на уровень реальных показателей влияет разный состав сравниваемых совокупностей по стандартизуемому признаку. Наоборот, если стандартизованные показатели повторяют соотношение реальных, то делают вывод о том, что на уровень реальных показателей разный состав по стандартизуемому признаку не влияет. Рассмотрим пример прямого метода (табл.43). Таблица 43. Распределение больных и умерших по отделениям боль- ниц А и Б (данные условные)
Косвенный метод стандартизации применяется тогда, когда показатели в сравниваемых группах неизвестны или известны, но недостаточно. За стандарт выбирают какой-то хорошо известный коэффициент (но не из числа сравниваемых) такого же характера, что и сравниваемый, и с ним с учетом его величины и структуры сравнивают имеющиеся недостоверные показатели. Косвенный метод стандартизации
 К ст. = число умерших Х К ст. = число умерших Х общ. показатель летальность стандарта ожидаемое число умерших А = (12х3) : 10,85 = 3,3 Б = (9х3) : 8,25 = 3,3 I действие - за стандарт принимают литера II рассчитываем ожидаемое число умерших больных с различными видами пневмонии в обеих больницах III Итоговый стандартный показатель действительное К ст. ________________________ Х стандарт ожидаемое Обратный метод стандартизации применяется тогда, когда необходимых для сравнения и оценки показателей нет. Их «конструируют» от «обратных» показателей, например, по данным о смертности и заболеваемости, которые следует возможно более объективно воспроизводить на основе имеющейся справочной информации численности и состава населения, среди которого и следует сравнить и определить заболеваемость и смертность. Расчет стандартизованных показателей (метод обратный косвенному) ожидаемое число больных К ст. ________________________ Х общий показатель летальности стандарта фактическое число больных К ст. (по больным); А = (373х3) : 360 = 3 К ст. (по больным); Б = (156х3) : 150 = 3 К ст. (по больным); В = (60х3) : 100 = 1,8
I дей-ие - расчитываем показатель летальности БолА= II дей-ие - выбор стандарта, стандарт берем из лиш-х данных III дей-ие – рассчитываем ожидаемое число пролеченных больных IV дей-ие – рассчитываем общее число ажидаемых больныз по 3-м больницам = 373 пролечили 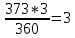 Вычисление коэффициента корреляции методом квадратом (по Пирсону)
Мср=62 dx=10-62=52 Rxy=-0.86 Вывод - сильная обратимая связь. Результаты достоверны если результаты t≥3 <-критерий корелляции. 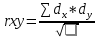 mr= 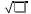 mr= 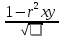 rxy= 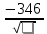 = -0.86 при n ≤ 30 , при n > 30 = -0.86 при n ≤ 30 , при n > 30t= 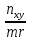 mr= 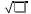 t= 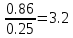 Задача: Дл/т=ср=М=ср=16
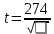 n=12 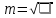 =0.12 =0.12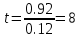 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
