Теоретические основы подготовки учащихся 11 класса к единому государственному экзамену по математике
 Скачать 263.38 Kb. Скачать 263.38 Kb.
|
|
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ КОЗЬМЫ МИНИНА» Факультет естественных, математических и компьютерных наук Кафедра физики, математики и физико-математического образования Направление подготовки _44.03.01- Педагогическое образование_ Профиль _Математика _ Курсовая работа на тему: «Теоретические основы подготовки учащихся 11 класса к единому государственному экзамену по математике» Выполнила: студентка группы МЗ-18-1 Балдина К. В. Научный руководитель: канд. пед. наук, доцент О.К. Огурцова Нижний Новгород 2022 Содержание Введение……………………………………………………………...….….3 § 1. Единый государственный экзамен по математике: цели проведения, особенности организации …? § 2. Уроки итогового повторения: цели проведения, особенности организации ……….……? § 3. Возможности использования уроков итогового повторения в ходе подготовки учащихся к единому государственному экзамену по математике …………….? Заключение…………………………………………………………..……? Список литературы………………………………………………….…..? Введение Цель современного образования имеет как внешнюю, так и внутреннюю направленность. Внешняя цель образования как государственного института состоит в жизнеобеспечении общества в конкретно-исторических условиях, в развитии его производительных сил, общей культуры и цивилизованности, в укреплении гражданского статуса отношений и морально-правовых устоев членов общества. Внутренняя целевая направленность образования заключается в развитии личностного потенциала, в овладении прочными знаниями, умениями и навыками с возможностью их применения на практике. Цели математического образования: – интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе; – овладение конкретными математическими знаниями, умениями и навыками, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования; – воспитание личности в процессе освоения математики и математической деятельности; – формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности. Содержание современного образования: Содержание математического образования основано на принципе реализации поставленных целей на небольшом по объему информационно емком и практически значимом материале, доступном для учащихся школьного возраста. При этом необходимо руководствоваться принципом преемственности, что обусловлено в первую очередь тем объективным фактом, что традиционное содержание обучения математике, сложившееся в течение многих десятилетий, отражает тот объем математических знаний, которые, с одной стороны, являются фундаментом математической науки, а с другой – доступны учащимся. Принцип преемственности должен сочетаться с современными тенденциями развития отечественной и зарубежной школы. Содержание математического образования можно представить в виде нескольких крупных блоков: арифметика; алгебра; функции; геометрия; анализ данных. Наряду с этими блоками естественно выделить методологические принципы, в которых содержание прослеживается с точки зрения развития общих методологических понятий и идей: математические методы и приемы рассуждений; математический язык; математика и внешний мир; история математики. Ниже представлено содержание блоков и описано распределение материала по ступеням обучения: – Арифметика. В начальной школе у учащихся формируются представления о натуральных числах как результате счета и измерения, о принципе записи чисел, вырабатываются навыки устных и письменных вычислений, накапливается опыт решения арифметических задач. При обучении в основной школе учащиеся приобретают систематизированные сведения о рациональных числах и овладевают навыками вычислений с ними, получают элементарные представления об иррациональных числах; уделяется внимание процентным расчетам, приемам прикидки и оценки, использованию калькулятора. В старшем звене вычислительный уровень совершенствуется в связи с введением новых операций, вычислением значений алгебраических, показательных, логарифмических и тригонометрических выражений. – Алгебра. В начальной школе учащиеся получают первоначальные представления об использовании букв для записи математических выражений и предложений, знакомятся с компонентами арифметических действий и учатся находить неизвестные компоненты по известным. В основной школе алгебраическое содержание формируется вокруг понятия «рациональное выражение»; учащиеся приобретают навыки преобразования целых и дробных выражений, получают представления об операции извлечения корня (на примере квадратных и кубических корней), знакомятся с понятием уравнения, приобретают алгоритмы решения основных видов рациональных уравнений, неравенств и систем. В старшем звене сосредоточен материал, относящийся к иррациональным, показательным и логарифмическим выражениям, расширяется класс изучаемых уравнений в связи с введением новых видов функций; развиваются представления об общих приемах решения уравнений, неравенств, систем. – Функции. Содержание обучения в начальной школе дает возможность изучения функций при введении буквенных выражений, при рассмотрении зависимостей между компонентами арифметических действий, при решении текстовых задач, в ходе которого используются зависимости между различными величинами (например, между скоростью, расстоянием и временем). При обучении в основной школе учащиеся приобретают систематизированные знания об элементарных функциях и их свойствах (прямая и обратная пропорциональность, линейная функция, квадратичная функция), приобретают навыки построения графиков. В старших классах развитие функциональной линии происходит в нескольких моментах: рассматриваются новые свойства функций; изучаются новые классы функций – тригонометрические, показательные, логарифмические функции; вводятся элементы математического анализа, которые находят применение при решении различных задач, связанных с исследованием функций, решением физических задач и т. п. – Геометрические фигуры. Измерение геометрических величин. При изучении геометрии предлагается отказаться от строго дедуктивного построения курса, усилив внимание к его наглядно-эмпирическому аспекту. Овладение пространственными формами должно проходить непрерывно, начиная с первых лет обучения, чему может способствовать усиление внимания к предметному моделированию стереометрических объектов в 5–6 классах и к рассмотрению планиметрических форм как составных частей пространственных – на следующей ступени обучения. – Анализ данных. В содержании этого блока естественным образом выделяются три взаимосвязанных направления, каждое из которых в той или иной мере проявляется на всех ступенях школы: подготовка в области комбинаторики с целью создания аппарата для решения вероятностных задач и логического развития учащихся, формирования важного вида практически ориентированной математической деятельности; формирование умений, связанных со сбором, представлением, анализом и интерпретацией данных; формирование представлений о вероятности случайных событий и умений решать вероятностные задачи. Уже на первой ступени школы учащиеся должны встретиться с задачами на перебор возможных вариантов и научиться находить необходимую информацию в таблицах, на диаграммах, в каталогах и т. д. В среднем звене в центре внимания оказывается понятие случайного события и его вероятности. Учащиеся знакомятся с вероятностными моделями реальных ситуаций, учатся находить и сравнивать простейшие вероятности случайных событий, приобретают навыки обработки реальных данных, получают представление об использовании электронно-вычислительной техники для хранения и обработки числовой информации. На старшей ступени обучения предполагается знакомство с основными вероятностно-статистическими закономерностями и вероятностно-статистическими моделями, характерными для отдельных отраслей знаний, особенностями сбора и обработки статистических данных в зависимости от целей исследования. – Принципиально важным является обучение математическому языку как специфическому средству коммуникации в его сопоставлении с реальным языком. Грамотный математический язык является свидетельством четкого и организованного мышления, и владение этим языком, понимание точного содержания предложений, логических связей между предложениями распространяется и на владение естественным языком и тем самым вносит весомый вклад в формирование и развитие мышления человека в целом. В 11 классе общеобразовательной школы по математике проводится Единый государственный экзамен (ЕГЭ). Он представляет собой форму государственной итоговой аттестации, проводимой в целях определения соответствия результатов освоения обучающимися основных образовательных программ среднего общего образования по математике требованиям федерального государственного образовательного стандарта. Для указанных целей используются контрольные измерительные материалы (КИМ), представляющие собой комплексы заданий стандартизированной формы. С 2015 г. ЕГЭ по математике проводится на двух уровнях: базовом и профильном. ЕГЭ базового уровня предназначен для проверки достижения участниками экзамена основных предметных результатов, в частности способности производить бытовые расчеты и использовать математические знания для решения задач, возникающих в повседневной жизни. ЕГЭ профильного уровня предназначен для проверки освоения более широкого круга математических понятий и методов, необходимых для продолжения математического образования. Базовый ЕГЭ по математике идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки. Профильный уровень ЕГЭ по математике переводится в 100-бальную систему. Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31. Итоговое повторение по математике тесно связано с подготовкой к ЕГЭ. Уроки повторения являются важной частью обучения математике школьников, поскольку на этих уроках происходит обобщение и систематизация знаний, полученных ими в течение года. В 11-ых классах такие уроки играют главную роль в подготовке учащихся к экзаменам. Особую роль при новой форме проведения выпускного экзамена приобретает организация итогового повторения. Теперь уже недостаточно привычных обобщения и систематизации знаний и способов действий. Не менее важным является необходимость формирования у выпускников умений: быстрее переключаться с одного типа заданий на другой; выбирать оптимальную стратегию при решении как одной задачи, так и всей работы в целом; проверять полученный результат решения. Тестовая система сдачи экзаменов создает значительные психологические проблемы для школьников с замедленной реакцией. Они обладают хорошими способностями, но не умеют быстро переключаться с одной задачи на другую. Это можно исправить, регулярно решая задачи, чему способствует использование тренировочных тестов, составленных по принципу тестов ЕГЭ. Подбирать тестовые задания надо таким образом, чтобы они максимально содействовали не формальному усвоению программного материала, а осознанному пониманию его и применению при решении задач на уровне узнавания и соотнесения с базовыми знаниями и способами действий. Различные виды повторения тесно взаимодействуют; от своевременного и успешного проведения одного из видов повторения, например, тематического или текущего, зависит продолжительность и успешность повторения другого вида — заключительного повторения или повторения в конце года. Перейду к краткой характеристике видов повторения. Повторение пройденного в начале года. При повторении в начале учебного года в первый план должно выдвигаться повторение тем, имеющих прямую связь с новым учебным материалом. Новые знания, приобретаемые на уроке, должны опираться на прочный фундамент уже усвоенных. При повторении в начале года необходимо наряду с повторением тем, тесно связанных с новым материалом, повторить и другие разделы, которые пока не примыкают к вновь изучаемому материалу. Здесь необходимо сочетать обе задачи: провести общее повторение в порядке обзора основных вопросов из материала прошлых лет и более глубоко повторить вопросы, непосредственно связанные с очередным материалом по программе учебного года. Текущее повторение пройденного. Текущее повторение в процессе изучения нового материала — весьма важный момент в системе повторения. Оно помогает устанавливать органическую связь между новым материалом и ранее пройденным. Текущее повторение может осуществляться в связи с изучением нового материала. В этом случае повторяется материал, естественно увязывающийся с новым материалом. Повторение здесь входит составной и неотъемлемой частью во вновь изучаемый материал. Под руководством учителя ученики на уроке воспроизводят ранее изученный ими необходимый материал. В результате этого доказательство новой теоремы воспринимается учащимися легко, а дальнейшая работа учителя — воспроизведение доказанного и упражнения, обеспечивающие вторичное осмысление теоремы и её закрепление. Во втором случае все связи с новым материалом, когда повторяемый материал не находит естественной увязки с новым и его приходится повторять на специальных уроках. При текущем повторении вопросы и упражнения могут быть предложены учащимся из различных разделов программы. Текущее повторение осуществляется в процессе разбора упражнений, включается в домашнее задание. Оно может быть проведено как в начале или в конце урока, так и во время опроса учащихся. Текущее повторение дополняется сопутствующим повторением, которое нельзя строго планировать на большой период. Сопутствующее повторение не вносится в календарные планы, для него не выделяется специальное время, но оно является органической частью каждого урока. Сопутствующее повторение зависит от материала, привлекаемого для изучения очередного вопроса, от возможности установить связи между новым и старым, от состояния знаний учащихся в данный момент. Успех сопутствующего повторения в значительной степени обусловливается опытом и находчивостью учителя. Сопутствующим повторением учитель по ходу работы устраняет неточности в знаниях, напоминает вкратце давно пройденное, указывает их связь с новым. Тематическое повторение. В процессе работы над математическим материалом особенно большое значение приобретает повторение каждой законченной темы или целого раздела курса. При тематическом повторении систематизируются знания учащихся по теме на завершающем этапе его прохождения или после некоторого перерыва. Для тематического повторения выделяются специальные уроки, на которых концентрируется и обобщается материал одной какой-нибудь темы. В процессе работы над темой вопросы, предлагаемые учащимся по каждому разделу, следует вновь пересмотреть; оставить наиболее существенные и отбросить более мелкие. Обобщающий характер вопросов при тематическом повторении отображается и на их количестве. Учителю приходится основной материал темы охватить в меньшем числе вопросов. Повторение на уроке проводится путём беседы с широким вовлечением учащихся в эту беседу. После этого учащиеся получают задание повторить определённую тему и предупреждаются, что будет проведена контрольная работа. Контрольная работа по теме должна включать все ее основные вопросы. После выполнения контрольной работы проводится разбор характерных ошибок и организуется повторение для их устранения. При тематическом повторении полезно составить вопросник, а затем логический план по теме и завершить работу составлением итоговых схем. Таблица или схема экономно и наглядно показывает общее для понятий, входящих в данную тему, их взаимосвязь в логической последовательности. Процесс составления таблиц в одних случаях, подбор и запись примеров после анализа готовой таблицы в других случаях является одновременно и формами письменных упражнений при обобщающем и систематизирующем повторении. Последовательное изучение различных особых случаев при повторении весьма полезно закончить их классификацией, что поможет учащимся яснее различить отдельные случаи и группировать их по определенному признаку. Заключительное повторение. Повторение, проводящееся на завершающем этапе изучения основных вопросов курса математики и осуществляемое в логической связи с изучением учебного материала по данному разделу или курсу в целом, будем называть заключительным повторением. Цели тематического повторения и заключительного повторения аналогичны, материал повторения (отбор существенного) весьма близок, а приемы повторения в ряде случаев совпадают. Вопрос использования уроков итогового повторения в ходе подготовки учащихся к единому государственному экзамену по математике рассматривали «Перевощикова Е.Н., Григорьева Т.П. К урокам тематического повторения в 7 классе // Математика в школе. – 1986. - № 3.» Уроки повторения вызывают у большинства учителей значительные трудности, поэтому нередко они превращаются в «натаскивание», в тренировку по решению задач, дублирующих варианты предстоящей контрольной работы. Акцент повторения нужно делать на систематизацию и обобщение знаний. Последовательность этапов урока повторения: работа с таблицей; самостоятельная работа на формирование умения выбирать главные положения, на которых строится обоснование тех или иных выводов; решение содержательных (комплексных) задач; решение нестандартных задач; творческое домашнее задание. Самостоятельная работа, направленная на формирование у учащихся умения проводить обоснования, - важнейший этап урока повторения. К этому этапу учитель подбирает несколько задач (одношаговые, двухшаговые, реже трехшаговые) по повторяемой теме. От обычных самостоятельных работ описываемая отличается тем, что от учащихся не требуется оформлять решения в обычном смысле (что заняло бы колоссальное время на уроке). Нужно только зафиксировать теоретический базис решения, т.е. дать перечень тех теоретических положений изученной темы, которые входят в обоснование решения задачи. Итак, вопрос подготовки учащихся 11 класса к единому государственному экзамену по математике исследован достаточно полно, но у большинства учителей вызывает трудность правильная организация уроков итогового повторения. Возникает противоречие между необходимостью подготовки учащихся 11 класса к единому государственному экзамену в процессе обучения математике и отсутствием необходимых методических рекомендаций. Все выше сказанное определяет актуальность проблемы исследования, которая состоит в разрешении указанного противоречия путем выявления теоретических основ подготовки учащихся 11 класса к единому государственному экзамену по математике. Объект исследования – процесс обучения математике в основной школе. Предмет исследования–методическая система подготовки учащихся 11 класса к единому государственному экзамену при обучении математике. Цель исследования – рассмотреть теоретические основы подготовки учащихся 11 класса к единому государственному экзамену при обучении математике. Для достижения поставленной цели необходимо решить ряд задач: - провести теоретический анализ психолого-педагогической, методической, математической литературы по проблеме организации единого государственного экзамена по математике; - рассмотреть особый тип уроков - уроки итогового повторения, цели их проведения, особенности организации; - выявить возможности использования уроков итогового повторения в ходе подготовки учащихся к единому государственному экзамену по математике. Для решения поставленных задач были использованы следующие методы: изучение литературы, изучение передового педагогического опыта, метод теоретического анализа и синтеза, метод восхождения от абстрактного к конкретному, метод моделирования. Методологической основой исследования послужили: концепция развивающего обучения математике (Азевич А.И., Перевощикова Е.Н., Григорьева Т.П. и др.); основные положения деятельностного подхода (Белошистая А.В. и др.); исследования по подготовке учащихся 11 класса к единому государственному экзамену в процессе обучения математике (Денищева Л., Краснянская К., Семенов П., Мельников Н. и др.). Курсовая работа состоит из введения, трёх параграфов, заключения и списка литературы (7 наименований). Общий объем работы ? страниц. ВЫРАЖЕНИЯ И ПРЕОБРАЗОВАНИЯ Пример 1 (В). Найдите значение выражения 32 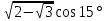 Решение: Воспользуемся формулой косинуса половинного угла: 32 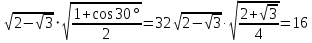 Ответ: 16. Пример 2 (С). Вычислите 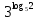 - -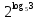 Решение. Найдем логарифм по основанию 5 каждой из степеней, входящих в разность. 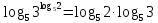 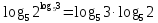 Таким образом, логарифмы обеих степеней, входящих в исходную разность, равны. Следовательно, 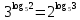 и и 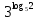 - -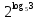 =0 =0От в е т: 0. [] ФУНКЦИИ. ГРАФИКИ. ПЛОЩАДИ П 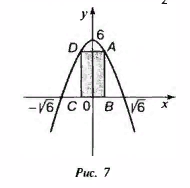 ример 1 (В). Из всех прямоугольников, две вершины которых лежат на оси Ох в интервале (- ример 1 (В). Из всех прямоугольников, две вершины которых лежат на оси Ох в интервале (-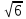 ; ; 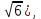 а две другие - на графике функции у = 6 - а две другие - на графике функции у = 6 - 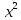 , найдите прямоугольник с наибольшей площадью. Чему равна эта площадь? , найдите прямоугольник с наибольшей площадью. Чему равна эта площадь?Решение. Пусть ABCD - искомый прямоугольник и В(х; 0), - 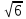 < х < < х < 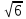 , тогда ОВ = х, АВ = 6 - х2 (рис. 7). Пусть S(x) - функция переменной , тогда ОВ = х, АВ = 6 - х2 (рис. 7). Пусть S(x) - функция переменнойплошали (точнее - ее половины) и S(x) = х(6- х2). Вычислим наибольшее значение функции S(x) на интервале (0; 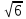 ), для чего найдем критические точки функции: ), для чего найдем критические точки функции:S'(x) = 6 - Зх2; 6 - Зх2 = 0. х = ± 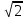 . .Из найденных точек только одна (х = 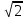 ) попадает в интервал (0; ) попадает в интервал (0; 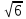 ). ).Так как на интервале (0; 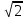 ) S'(x) > 0, а на интервале ( ) S'(x) > 0, а на интервале (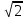 ); );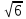 ) S'(x) < 0, то х = ) S'(x) < 0, то х = 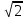 ) – точка максимума функции S(x). Поскольку это единственный максимум на интервале и функция непрерывна на области определения, то наибольшее значение функция принимает в точке х = ) – точка максимума функции S(x). Поскольку это единственный максимум на интервале и функция непрерывна на области определения, то наибольшее значение функция принимает в точке х = 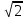 . .Площадь наибольшего прямоугольника равна 2 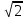 <(6-2) = 8 <(6-2) = 8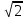 . .Ответ: размеры прямоугольника 2 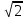 на 4, его площадь 8 на 4, его площадь 8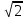 . [] . []УРАВНЕНИЯ И НЕРАВЕНСТВА Рациональные уравнения и неравенства. Пример (В). При каких целых значениях параметра р выполняется равенство sin a = 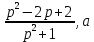 ∈ (0; ∈ (0;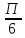 )? )?Решение. По условию 0< а< 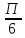 , следовательно, 0 , следовательно, 0Таким образом, мы пришли к системе неравенств: 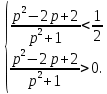 Так как р2 + 1 > 0, то система приобретает вид: 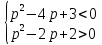 , ,решение первого неравенства 1 < р < 3, решение второго неравенства р∈R. Таким образом, решение системы – промежуток (1;3). Единственное целое решение системы - число 2. Ответ: 2. Пример (С). Дано уравнение с целыми коэффициентами х3 + 3х2 + рх + q =0. Найдите наибольшее целое значение параметра р, при котором это уравнение имеет три различных корня, один из которых равен -1. Решение. При подстановке х = -1 в данное уравнение, получим q = р - 2. Теперь подставим значение q в исходное уравнение: х3 + 3х2 + рх + р - 2 = 0. Разложим многочлен, стоящий в левой части уравнения, на множители, один из которых равен х + 1 ( поскольку число -1 корень данного уравнения). х3 + х2+2х2+2х-2х+рх+р-2= х2(х+1)+ 2х(х+1)+ х(р - 2) + р - 2 =(х + 1 )(х2 + 2х + р - 2) По условию данное уравнение имеет три корня, один из которых число -1 .Следовательно, квадратное уравнение х2 + 2х + р -2 = 0 с дискриминантом, равным 12 - 4р, должно иметь два корня, что возможно при р < 3. Наибольшее целое число, удовлетворяющее этому неравенству, есть число 2. Ответ: р = 2. 2. Иррациональные уравнения, неравенства. Пример (В). Найдите сумму корней уравнения х2 - 5x+6 = 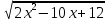 Решение. Преобразуем исходное уравнение: х2 - 5x+6 = 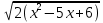 Введем новую переменную у = х2 - 5х + 6 (у≥0). Тогда уравнение примет вид: у2 - 2у = О. Его решениями будут числа 0 и 2. Перейдя к исходной переменной х, получим совокупность уравнений 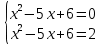 корни которой - числа 1, 2, 3, 4. Их сумма равна l0. Ответ: 10. Пример (С). Найдите все пары чисел (х ; у), удовлетворяющие уравнению 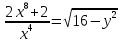 . .Решение. Запишем уравнение в виде 2х4 + 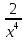 = =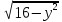 . Так как 0≤ . Так как 0≤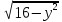 ≤ 4, то равенство возможно, когда ≤ 4, то равенство возможно, когда2х4+ 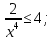 х4+ х4+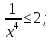 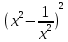 ≤0. ≤0.Таким образом, х2- 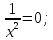 х4=1, х=±1. х4=1, х=±1.При х = ±1, 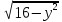 =4 и у= 0. =4 и у= 0.Ответ: (-1 ; 0); ( 1 ; 0). 3. Логарифмические и показательные уравнения, неравенства Пример (В). При каких значениях параметра b уравнение 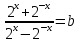 не имеет решений? Решение. Умножим числитель и знаменатель дроби из левой части уравнения на 2х. Тогда уравнение примет вид 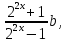 при х≠0 получаем 22х+1=b⋅22х-b , т.е. 22х(b - 1 ) = b + 1. Если при х≠0 получаем 22х+1=b⋅22х-b , т.е. 22х(b - 1 ) = b + 1. Еслиb = 1, то полученное уравнение не имеет решений, если же b≠1, то его можно записать в виде 22х= 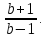 Последнее уравнение не имеет решений, если 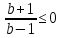 , т.е. при b∈ , т.е. при b∈ 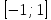 . .Ответ: b∈ 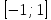 . .Пример (С). Пара чисел (х0; у0) – решение системы 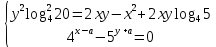 При каких значениях параметра а выполняется условие х0 > у0? Решение. В первом уравнении системы выделим полный квадрат. 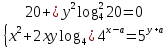 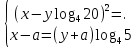 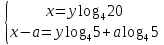 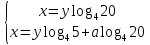 Приравняв правые части уравнений системы, найдем у. Решением исходной системы будет пара чисел 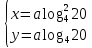 Пусть х0 > у0, а 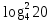 >а >а 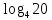 , тогда , тогда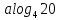 ( (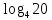 - 1) >0, а - 1) >0, а 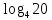 · · 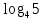 >0. >0.Так как 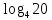 >О и >О и 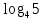 > 0, то а> 0. > 0, то а> 0.Ответ: а> 0. 4. Тригонометрические уравнения, неравенства. Пример (В). Определите знак выражения sin2003 - sin2002 + 1 . Решение . Представим выражение в виде sin2003 - sin2002 + 2003 - 2002, или (sin2003 + 2003) - (sin2002 + 2002). Рассмотрим функцию f(x) = sinx + х, ее производная равна: f '(x) = cosx + 1, f '(x) ≥0 для любого х. Следовательно, f(x) - возрастающая функция, т.е. sin2003 + 2003 > sin2002 + 2002, или sin2003 - sin2002 + 1 > О. Ответ: sin2003 - sin2002 + 1 > О. Пример (С). Решите уравнение З(tgx - ctg х) = 4sin2х. От в е т: ± 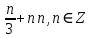 [] []ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ИХ СВОЙСТВА. ИЗМЕРЕНИЕ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН Пример (В). Тело состоит из двух равных усеченных конусов, имеющих общее большее основание и расположенных пo разные стороны от него. Образующая конуса равна 6 см и в два раза больше радиуса меньшего основания. Найдите поверхность сферы, вписанной в это тело. Ответ: 108п см2. Пример (С). В правильную треугольную призму вписан шар. Найдите полную поверхность призмы, если объем шара равен 288л дм3 От в е т: 648 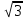 см2. см2.С педагогической точки зрения отечественный тест ЕГЭ представляет собой тест успеваемости. Теоретически тесты успеваемости подразделяются на два вида: тесты скорости и тесты мощности. По тестам скорости у испытуемых обычно не хватает времени ответить на все вопросы. По тестам мощности у каждого такая возможность есть, но только возможность, поскольку в таком тесте всегда содержатся заведомо трудные задания, обычно непосильные для большинства испытуемых. В тестах ЕГЭ по математике их авторы постарались соединить «в одном флаконе» оба направления. По признаниям самих авторов теста, предполагается, что решить все его задания абсолютно правильно за отведенное время может один из 10 000 школьников. Опыт показывает, что реально за отведенное время и в жестких условиях атмосферы ЕГЭ ответить полностью правильно на все вопросы не может даже большинство учителей математики. Автор этой статьи неоднократно проводил такой опыт: предлагал тест ЕГЭ выпускникам V курса физико-математического факультета на сдвоенной паре, т.е. на 3 часа. Результаты блестящими не назовешь. Сказанное не имеет целью утвердить кого-то в мнении, что ситуация безнадежна. Напротив, автор имеет целью подвести читающего к пониманию того, что подготовка к успешному написанию ЕГЭ отличается от привычной нам методики обучения школьников математике «вообще». Внешне тест ЕГЭ отличается от обычной контрольной работы только количеством заданий: в контрольной работе их обычно не более 5–6, в тесте ЕГЭ их количество колеблется от 25 до 32 (в разные годы). Однако внутренне тест ЕГЭ значительно отличается от обычной контрольной работы. Его авторы взяли за образец направленность американского «теста достижений» по математике (тест на готовность к получению высшего образования SAT) на максимальную стимуляцию нестандартного мышления при его выполнении. Все задания ЕГЭ честно составлены в пределах школьной программы. Но уже первый сборник заданий ЕГЭ был для учителей просто «шоковой терапией». Он напрочь ломал целый арсенал привычных методических подходов к обучению математике: начиная от необходимости полного отказа от всех правил оформления решения до совершенной нестандартности в формулировках заданий. В тестах полностью разрешен «метод тыка» (кстати, весьма эффективный в разделах А и В, если владеть технологией его применения). Надо сказать, что использование этого метода в американских тестах достижений является узаконенным и пропагандируемым. Мы привыкли учить школьника решать задачу, а практически все американские руководства по подготовке к тестированию советуют школьникам учиться подбирать наиболее разумный ответ или тренироваться в его угадывании. Именно такой подход позволяет получить наибольшее количество баллов, поскольку американский тест по математике для выпускника содержит от 30 до 45 вопросов, а времени для его написания дается ровно 30 мин. Психологическая подготовка к ЕГЭ 1. Итак, первое, что мы советуем начать делать уже завтра: прекратить пугать учеников предстоящим ЕГЭ, и начать формировать в них твердое убеждение в том, что, если очень постараться, то можно получить вполне приличный балл: время для подготовки еще не полностью потеряно. Конечно, не следует «перегибать палку» и внушать школьникам, что ЕГЭ – это легко и просто. Но не нужно и внушать им мысль о полной безнадежности. Автор этого материала никогда не проводит «входную» контрольную работу, чтобы определить уровень знаний и умений ученика, но всегда начинает разговор со школьниками, приходящими на подготовительные курсы, с прямого вопроса: «Что каждый из Вас хочет получить на ЕГЭ?» Таким образом, сразу определяется планируемый результат обучения. Важно, чтобы школьник сам его честно сформулировал для себя. Этот разговор дает возможность учитывать «актуальный потолок» обучаемого. Это не значит, что следует его занижать, или что этот «потолок» неизменен и, однажды его наметив, на него следует постоянно ориентироваться. Например, автор этой статьи всегда ставит себе опережающую цель: дать «на выходе» результат на 1 балл выше, чем это определено самим школьником в первой предварительной беседе. В этой связи, уровень сложности заданий в некоторых случаях следует объявлять заранее, а в некоторых – только после его выполнения: «Как вы думаете, из какого раздела было это задание? Из раздела В! (или С!) И вы его сделали! Кому оно показалось невероятно трудным? Никому? Молодцы! Идем дальше: из какого раздела хотите следующее задание?» Понятно, что это психологически продуманная игра, но при спланированном подборе заданий она приводит к очень значимому сдвигу как в самооценке школьника, так и в его чувстве уверенности в себе, а также к некоторым положительным подвижкам в качестве его знаний и умения их применять. А главное, в умении «технично» сдавать тест, используя всевозможные вспомогательные приемы и соображения. 2. Следует учить школьника технике сдачи теста. Эта техника включает следующие моменты: а) обучение постоянному жесткому самоконтролю времени; б) обучение оценке объективной и субъективной трудности заданий и соответственно разумному выбору этих заданий; в) обучение прикидке границ результатов и минимальной подстановке как приему проверки, проводимой сразу после решения задания; г) обучение приему «спирального движения» по тесту. Начнем с последнего пункта г). Данный прием находится в полном несоответствии с действующей методикой обучения школьника математике. Но он является первым необходимым приемом для успешного написания задания типа «тест с ограничением времени». Он состоит в следующем: ученик сразу просматривает тест от начала до конца и отмечает для себя то, что кажется ему простым, понятным и легким. Именно эти задания школьник выполняет первыми. Я говорю так: «Начинайте с того, что вы можете выполнить сходу, без особых раздумий. Пробегите глазами по разделу В и отметьте два-три задания, которые вы поняли сразу. К ним вы перейдете, когда закончите с разделом А. Просмотрите раздел С – один пример в этом разделе всегда решаем без особого напряжения (это действительно так). Отметьте то, что вы попробуете решить, когда закончите с разделом В. Ученик может сделать так несколько раз (двигаясь по спирали и выбирая то, что «созрело» к данному моменту). Если он ориентируется на тройку, то после того, как решил всё, что мог из раздела А, он попробует решить что-то из раздела В (намеченные ранее 2–3 пункта). А может быть он справится с одним примером из раздела С? Стоит попробовать. По пункту а): При ориентации на 4 следует предупредить школьников, что они должны уложиться с разделом А в первый час. Что не успели за 1 час, следует оставить (и вернуться при наличии времени после). За второй час следует решить все, что удастся из раздела В. Третий час можно посвятить разделу С. В оставшийся час (если тестируемый чувствует, что ни в пункте В, ни в С ему больше ничего не одолеть) следует вернуться к разделу А и решить всё, что в нем осталось и может быть решено (добрать баллы «на мелочи»). Таким же образом должен действовать тот, кто планирует получить 5. В этом случае весь раздел А следует «уложить» в 40–45 мин (или меньше). В разделе В нужно сделать не менее 7–8 заданий за 1 час. В разделе С не менее 1–2 заданий. На это может уйти 1–1,5 часа. Эти временные затраты школьник должен все время помнить – это и есть постоянный и жесткий контроль времени. Естественно, выдержать этот график может только тот, кто приучен три часа подряд заниматься математикой с полной отдачей! Надо сказать, что только небольшая часть школьников способна на это без специальной подготовки. Учителя, присутствующие на ЕГЭ, подтвердят, что очень часто еще остается много времени, но школьник отказывается продолжать работу: «устал», «не могу больше», «не соображаю», «не хочу». Таким образом, отсутствие привычки напрягаться в математике несколько часов подряд без перерыва – одна из важных причин низкого качества написания теста многими школьниками. У них есть привычка выдерживать 45 мин урока математики, максимум – 1,5 часа, если в школе практикуются сдвоенные уроки, но при этом между ними всегда есть перерыв, которого нет на ЕГЭ. Выдержать 3,5 часа без перерыва и при этом интенсивно работать большинство школьников не может. К такому режиму работы нужно приучать и тренировать в нем учеников хотя бы 1 раз в неделю. Если иногда практиковать занятия хотя бы по 2 часа без перерыва, то сначала дети очень устают, но уже через месяц адаптируются к такому режиму и работают 1,5–2 часа «на одном дыхании», даже слабые ученики. По пункту б). Учащиеся обычно сами достаточно хорошо знают, где у них особо слабые места. Этих слабых мест следует избегать при выполнении теста. Многие, например, боятся логарифмов, поскольку эта тема во многих случаях изучается только в ХI классе, и учитель зачастую старается дать эту тему более сжато, а значит, плохо ее закрепляет. Но логарифмы – одна из любимых тем составителей ЕГЭ, и если их опустить, то нужно решать всё, что связано с тригонометрией, иначе шансов набрать хороший балл нет. А тригонометрия объективно труднее для многих школьников со всех точек зрения. Я легко убеждаю школьников в том, что логарифмические и показательные уравнения (или неравенства) решать легче, чем выполнять задания по тригонометрии. При этом я всего лишь сравниваю количество формул, которое нужно знать, чтобы ориентироваться в каждом из этих разделов. Естественно, в тригонометрии их намного больше. Кроме того, для решения логарифмических или показательных уравнений (или неравенств) необходимо освоить небольшое количество типовых приемов (4–5), которые универсально работают на заданиях любой сложности. А в тригонометрии нужно каждый раз искать новый оригинальный подход, особенно если не знаешь наизусть всех формул и следствий из них. Это не значит, что не следует заниматься тригонометрией, просто более слабым школьникам выгоднее сосредоточиться на логарифмах и показательных уравнениях, чем пытаться перед самым ЕГЭ «одолеть» тригонометрию. Ограничив для себя объем заданий, которые он наверняка должен решить, школьник будет иметь возможность посвятить подготовке к ним больше времени, что повышает шансы на успех. Понятно, что этот совет в корне противоречит всем нашим методическим установкам – учитель всегда ориентирован на то, чтобы заниматься более всего ликвидацией пробелов в знаниях школьника. И это правильно, если иметь в виду объем его знаний. Однако если мы ставим себе задачу подготовить школьника к успешному написанию теста ЕГЭ (именно как теста), то наша цель: подготовить его так, чтобы он самостоятельно сумел набрать максимально возможное для него количество баллов. А в этом случае всем известное изречение «лучше меньше, но лучше» оказывается справедливым. Если школьник планирует решать геометрическую задачу в разделе В, то из двух заданий, содержащихся в нем, одна задача планиметрическая, другая – стереометрическая. Объективно считается, что стереометрическая задача труднее, чем планиметрическая, поскольку стереометрия изучается в ХI классе как материал более сложный. Но в тестах прошлых лет планиметрическая задача всегда была сложнее, чем стереометрическая, поскольку требовала применения таких свойств, которые школьники давно забыли или вообще не знали. Нужное свойство могло быть рассмотрено автором учебника геометрии как задача на доказательство и опущена учителем как не являющаяся необходимой в процессе изучения материала. По пункту в). Следует учить школьников простым подстановкам для проверки результатов сразу (а не «если останется время»). Особое внимание нужно обращать на скобки, закрывающие интервалы: всегда внимательно проверять, входят ли концы интервалов в область допустимых значений, поскольку часто разница в записи ответов составляет лишь разницу в форме скобок. После решения задания школьник должен снова внимательно перечитать текст его условия (что нужно было найти?), поскольку в условии может содержаться дополнительное требование. Многие школьники просто не обращают внимания на эти требования, записывая при верно решенном задании неправильный ответ на него в бланк теста. Правда, чаще всего эти дополнительные условия содержатся в заданиях раздела В, а не А. Методическая подготовка к ЕГЭ Часто учителя, репетиторы и родители, помогающие своим детям подготовиться к ЕГЭ, пытаются прорешать как можно больше вариантов предыдущих лет. Опыт показывает, что такой путь неперспективен. Во-первых, варианты не повторяются. Во-вторых, у школьника не формируется устойчивый общий способ деятельности с заданиями соответствующих видов. В-третьих, у школьника появляется чувство растерянности и полной безнадежности: заданий так много и все они такие разные, и каждый раз нужно применять соответствующий подход. Иными словами, уже через неделю школьник не может вспомнить, как он решал это задание. Причем нетвердо владеющий общими способами деятельности с материалом школьник пытается именно вспомнить соответствующее решение, а не применить общий подход к заданиям такого типа. Естественно, запомнить все решения всех заданий невозможно. Поэтому намного разумнее учить школьников общим универсальным приемам и подходам к решению. Сформулируем принципы построения методической подготовки к ЕГЭ. Первый принцип – тематический. Разумнее выстраивать такую подготовку, соблюдая «правило спирали» - от простых типовых заданий до заданий со звездочками, от комплексных типовых заданий до заданий раздела С. Второй принцип: на этапе подготовки тематический тест должен быть выстроен в виде логически взаимосвязанной системы, где из одного вытекает другое, т.е. выполненный сегодня тест готовит к пониманию и правильному выполнению завтрашнего. Третий принцип: переход к комплексным тестам разумен только в конце подготовки (апрель–май), когда у школьника накоплен запас общих подходов к основным типам заданий и есть опыт в их применении на заданиях любой степени сложности. Четвертый принцип: все тренировочные тесты следует проводить с жестким ограничением времени. Занятия по подготовке к тестированию нужно стараться всегда проводить в форсированном режиме с подчеркнутым акцентированием контроля времени. Темп такого занятия учитель должен задать сразу и держать его на протяжении всех 45 мин. во что бы то ни стало, используя время занятия до последней секунды. Этот режим очень тяжел школьникам на первых порах, но, привыкнув к этому, они затем чувствуют себя на ЕГЭ намного спокойнее и собраннее. Пятый принцип: максимализация нагрузки (по содержанию и по времени) для всех школьников в равной мере. Это необходимо, поскольку тест по определению требует ставить всех в равные условия и предполагает объективный контроль результатов. Шестой принцип в шутливой форме звучит так: «Нормальные герои всегда идут в обход!» Он взят из фильма «Айболит – 66», где «герои» пели песенку с такими словами. Смысл этого принципа в следующем: нужно учиться использовать наличный запас знаний, применяя различные «хитрости» и «правдоподобные рассуждения» для получения ответа наиболее простым и быстрым способом. [] Некоторые особенности итоговой аттестации школьников: Единый государственный экзамен в форме тестирования Контрольно-измерительные материалы (КИМы) Внедрение новой формы итоговой аттестации выпускников школ поставило перед обществом громадную, в некоторой степени революционную задачу: оценить всех выпускников всех школ всех регионов России одним измерителем. В качестве таких измерителей выступают контрольно-измерительные материалы, представленные в тестовой форме. КИМы представляют собой систему специально подобранных проверочных заданий специфической формы, позволяющую количественно оценить учебные достижения учащихся в одной или нескольких областях знаний. Тестовые задания упорядочены в рамках определенной стратегии их предъявления учащимся и обеспечивают информативность оценок уровня подготовки испытуемых. Поскольку контрольно-измерительные материалы служат средством измерения (инструментом), с помощью которого реализуется процедура стандартизированного тестирования, то далее рассмотрим структуру КИМов и виды заданий экзаменационной работы, некоторые общие подходы к оцениванию результатов. Содержание КИМов определяется на основе примерных программ общеобразовательных предметов, разработанных Министерством образования и науки Российской Федерации для общеобразовательных учреждений, и не может выходить за пределы указанных программ. Это означает, что дополнительные знания по предмету для успешной сдачи ЕГЭ не требуются. В процессе осуществления эксперимента изменялось количество заданий экзаменационной работы, время на ее выполнение. Отрабатывалась методика начисления баллов за выполнение каждого типа задания и оценивания всей работы. За 2002-2009 годы сложилась вполне определенная структура экзаменационной работы по математике. В ней выделялись три части, соответствующие базовому, повышенному и высокому уровням усвоения проверяемого материала. Ниже в таблице приведены данные об изменении числа заданий в каждой части и времени на выполнение всей работы за 2002 -2009 годы. Таблица Число заданий и время выполнения экзаменационной работы по математике 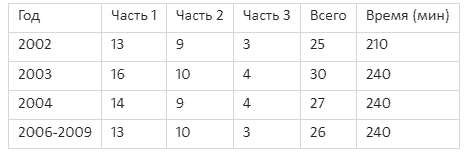 В работе 2002 г. с помощью 25 заданий не удалось охватить проверкой некоторые важные умения, традиционно проверявшиеся на вступительных экзаменах в вузы. В связи с этим в 2003 г. изменилось число заданий, их распределение по частям и время на выполнение работы. Работа уже включала 30 заданий, распределенных на три части, и время выполнения было увеличено до 240 минут. Как видно из таблицы, в последующие годы число заданий уменьшилось (до 26 в 2006-2009 годах), а время на выполнение работы осталось 240 минут. В контрольно-измерительные материалы (2002-2009г.г.) включены задания трех типов - А, В и С: • к типу А относят задания с выбором ответа; • к типу В относят задания с кратким дополняемым ответом в виде числа, формулы, слова и т.п.; • к типу С относят задания со свободно конструируемым ответом, не регламентированным по длине и форме представления. В указанный период задания в каждом варианте экзаменационной работы распределялись по трем частям, которые различались по назначению, по содержанию, по сложности включенных в них заданий. Рассмотрим более подробно содержание этих частей на примере варианта ЕГЭ по математике в 2006 году, опубликованного в качестве проекта для обсуждения Федеральным институтом педагогических измерений. Дадим краткую характеристику частей варианта единого государственного экзамена. |
