Теоретические основы подготовки учащихся 11 класса к единому государственному экзамену по математике
 Скачать 263.38 Kb. Скачать 263.38 Kb.
|
|
2. Самостоятельная работа. К этой части урока учитель заранее пишет задания на боковой части доски. До нужного момента урока эти записи скрыты или шторками, или «крыльями» доски. Во время предъявления заданий учитель подчеркивает, что их решать не надо, а следует только указать теорему, формулу, правило, на которых основывается решение. Задания: 1) Составить квадратное уравнение, имеющие корни х1=2, х2=4. 2) Найти сумму и произведение корней квадратного уравнения: а) х2-3х+6=0; б)х2-5х+6=0. 3) Найти подбором корни уравнения х2-8х-20=0. 4) Решить уравнения: а) х2-6х+8=0; б) 2х2-3х+1=0; в) 4х2+25=0; г) х2-5х=0. (Напомним: в данных случаях учащиеся не должны находить корней, их задача – указать только подходящие формулы или правила.) 3. Решение комплексных задач. Учитель записывает уравнения а) х4-3х2-4=0, б) 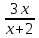 + +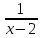 = = и предлагает ответить на следующие вопросы: «Как называются эти уравнения? Как привести их к квадратным? В чем особенность решения второго из данных уравнений?» Затем в классе решают второе уравнение. При этом они вспоминают свойства уравнений, формулу корней, находят посторонний корень, т.е. вспоминают определение корня, а также повторяют ряд понятий из курса алгебры 6 класса: формулу разности квадратов, раскрытие скобок и приведение подобных членов, операции над алгебраическими дробями. 4. Решение нестандартной задачи: «Найти наиболее рациональным способом корни уравнения 1978х2-1984х+6=0». Учащиеся замечают, что сумма коэффициентов равна 0, следовательно, х=1 – корень. Второй корень легко отыскивается, если перейти от данного уравнения к приведенному и применить теорему, обратную теореме Виета, значит, х2=6/1978, или х2=3/989. Целесообразно разобрать и второй способ решения: х2  , ,х2 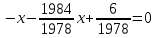 , ,х(х 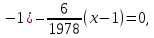 (х 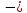 1)(х 1)(х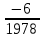 )=0, х1=1, х2= )=0, х1=1, х2=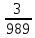 . .5. Творческое домашнее задание. В домашнем задании к описываемому уроку ученики должны были составить квадратные уравнения к нескольким текстовым задачам. Теперь им предстоит выполнить задание, обратное тому, что они делали дома: а) придумать задачу, которую можно решить с помощью уравнения х2-х-6=0; б) придумать задачу, решаемую с помощью квадратного уравнения с корнями 3 и -2, для которой лишь число 3 – является решением. [7]  Урок систематизирующего повторения по теме «Четырёхугольники». Урок систематизирующего повторения по теме «Четырёхугольники».1. Работа с таблицей. Учитель вывешивает в классе заранее подготовленную табл.2 и по ней разбирает с классом следующие вопросы: Таблица 2. Параллелограмм.
  Прямоугольник Ромб
Квадрат
Какие виды четырехугольников вы знаете? Дайте соответствующие определения. Если в условии задачи или теоремы дан ромб MNPQ, то какие следствия можно получить? Истинность каких утверждений достаточно проверить, ели в задаче требуется доказать, что четырехугольник PQRS является параллелограммом? Перечислите свойства квадрата и попытайтесь при этом ответить на следующий вопрос: от какого четырехугольника «унаследовал» квадрат то или иное свойство. При разборе этих вопросов учитель обращает внимание семиклассников на возможность неоднозначного подхода к определениям некоторых фигур ( в табл.2 отражено два подхода к определению квадрата). 2. Самостоятельную работу учащиеся выполняют на листочках с копиркой. Первые экземпляры работы они сдают учителю, а по вторым контролируют себя сами при устной проверке в классе. Содержание самостоятельной работы. В табл.2 кратко записаны определения некоторых фигур и чертежами представлены их свойства и признаки. Укажите номер определения, свойства или признака, который необходим для решения каждой из следующих задач: Сумма двух углов параллелограмма равна 168°. Найдите его углы. Дано: ABCD – прямоугольник (рис.1), ∟1=58°. Найдите: ∟2,∟3. Дано: ABCD – ромб (рис.2), AC=AB. Найдите: ∟BAD, ∟ABC. Дано: PQRS – квадрат (рис.3). Найдите: ∟1,∟2. Дано: PQRS – выпуклый четырехугольник (рис.4), ∟P+∟Q =180°, ∟P=∟R. Докажите, что PQRS – параллелограмм. Дано: ABCD – параллелограмм (рис.5), AK=CM. Докажите, что BKDM – параллелограмм. При проверке самостоятельной работы на уроке учитель должен особо подчеркнуть следующий момент: утверждать, что данный четырёхугольник является параллелограммом (прямоугольником, ромбом, квадратом), мы можем на основании либо определения, как в задаче 5, либо признака параллелограмма (прямоугольника, ромба, квадрата), как в задаче 6.
Вот на этом этапе урока и идет наиболее интенсивно подготовка к контрольной работе. Характерные элементы из предстоящей контрольной работы включены в содержание данной самостоятельной работы, а при проверке учитель в первую очередь обращает на них внимание. | ||||||||||||||||||||||||

 1) В С
1) В С 
 Свойства и признаки:
Свойства и признаки:




 2) 3) 4) 5)
2) 3) 4) 5) 






 6)
6)



 8) В С
8) В С







 9) 10)
9) 10) В С
В С




















 13) 14) 15) 16) 17)
13) 14) 15) 16) 17) 

 Рис.1
Рис.1 2 0
2 0 Рис.2 В
Рис.2 В



 Рис.4
Рис.4
 Q R
Q R
 Рис.5 C
Рис.5 C








 B C
B C O Q
O Q