Теоретические основы подготовки учащихся 11 класса к единому государственному экзамену по математике
 Скачать 263.38 Kb. Скачать 263.38 Kb.
|
|
Часть вариантов экзаменационной работы содержала показательные уравнения, сводимые к представленным выше уравнениям методом разложения на множители. С подобными уравнениями справились от 50 до 66% учащихся . Логарифмические уравнения. Наиболее простые логарифмические уравнения, включенные в 1 часть, имеют вид и являются квадратными относительно выражения . Например, «Найдите сумму корней уравнения Успешно выполнили подобные задания 66% учащихся. Во 2 часть были включены уравнения, которые сводятся к квадратным относительно некоторого выражения. Например, « Найдите произведение корней уравнения Отметим, что с подобными заданиями справляется менее трети выпускников средней школы. Тригонометрические уравнения. В вариант ЕГЭ были включены тригонометрические уравнения двух типов. Первый тип: «Укажите наибольший отрицательный корень уравнения »; « Решите уравнение; второй тип: « Решите уравнение 3sinx=sin2x»; «Укажите число корней уравнения tg2 х - tgx = 0 на промежутке (- 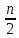 ; п) ». ; п) ».С уравнениями первого типа (sin (ах + b) = m, cos (ах + b) = m) справились от 47 до 61 % учащихся. Вместе с тем уравнения того же вида, но содержащие тангенс, решаются учащимися значительно хуже (от 18 до 32%). Возможно, это объясняется тем, что в программе и в учебниках большее внимание и большее число часов отводится на изучение уравнений вида sin х = а, cos х = а, по сравнению с уравнениями tg х = а, ctg х =а. Второй из указанных типов тригонометрических уравнений, решаемый разложением на множители, выполнили от 46 до 77% учащихся. Уравнения смешанного типа. Например, «Сколько корней имеет уравнение (1-2sin2 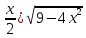 =0?» =0?»Результаты выполнения этого задания составляют достаточно большой интервал от 8 до 42%. Отметим, что если уравнение содержит произведение тригонометрической и логарифмической функций, то число правильных ответов учащихся находилось в интервале 28-29%. Хуже (8%) справились с уравнением, которое содержало произведение тригонометрической функции и квадратного корня. Кроме того, в этом уравнении был самый длинный числовой промежуток [-5; 5], на котором нужно было сделать отбор корней, что, возможно, явилось дополнительным источником ошибок. Системы уравнений. С решением систем справились от 30 до 45% учащихся (не учтены результаты выполнения подобных заданий в четырех вариантах). Отметим, что в четырех неучтенных вариантах решение системы можно было найти только графическим методом. Невысокие результаты (16-25%), полученные при их выполнении, явно указывают на недостаточное внимание к графическому методу решения систем. Дополнительный анализ условия этих заданий показал, что самые низкие результаты (16%) были в том случае, когда сначала требовалось выполнить упрощающее алгебраическое преобразование, применив тождество. Неравенства. В вариантах присутствовали лишь логарифмические неравенства базового уровня сложности. Например, « Решите неравенство log0,8(0,25-0,lx)>-1 ». С необходимостью решать показательное неравенство учащиеся сталкивались при выполнении заданий на отыскание области определения функции, например, « Найдите область определения функции y = 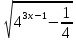 ·» ·»Применять метод интервалов к решению рациональных и дробно-рациональных неравенств требовалось при решении заданий на исследование функций с помощью производной. Решили логарифмические неравенства от 42 до 77% учащихся. Следует отметить, что выпускники несколько лучше решали неравенства, в которых основание логарифма было больше единицы. [6] ФУНКЦИИ И ИХ СВОЙСТВА Задания на нахождение области определения сложной функции, где нужно показать умение решать простейшие показательные неравенства (53x-1-1≥0), выполнили от 36 до 74% учащихся. При этом успешность выполнения такого задания находится в явной зависимости от того, каков характер монотонности показательной функции. В случае ее монотонного возрастания процент правильных ответов значительно выше, чем в случае, где показательная функция является монотонно убывающей. Учащиеся допускают типичную ошибку при переходе от неравенства ах≥ах0 к неравенству х ≤ х0 при 0 < а < 1. В заданиях на нахождение множества значений функции лучше (от 43 до 66%) решаются те задания, в которых область значений «считывается» по графику функций. Хуже выполняются задания, в которых нужно применить аналитический метод. Например, « Найдите область значений функции у= 3 + cosx», «Найдите область значений функции у= 2 - sin2x». С подобными заданиями справились от 34 до 69% учащихся. В различных вариантах проверялось умение учащихся по заданному графику определить («Прочесть»), обладает ли функция требуемым свойством (четная или нечетная, возрастающая (убывающая) на указанном промежутке и т.п.), или указать область ее значений. Умеют найти промежутки монотонности 87% учащихся, увидеть график четной (нечетной) функции - от 45 до 76%, хуже находят точки экстремумов (51 %). В 1 части проверялись умения найти производную и первообразную функции, а также владение геометрическим смыслом производной. Результаты выполнения заданий показали, что учащиеся владеют таблицей производных, при этом ими успешнее (от 46 до 78%) выполняются задания, где нужно найти производную суммы двух функций, явно меньше учащихся сумели найти производную сложной функции (39%). Примерно те же результаты (47 до 81%) показали учащиеся и при нахождении первообразных для заданной функции, применяя для решения таблицы первообразных, и правила для их нахождения или определение. Хуже всего находят первообразную для функции вида у= f(kx + b); только 40% учащихся выполнили такие задания. Понимание геометрического смысла производной проверяется в различных вариантах заданиями двух типов. Первый тип: по графику функции у = f(х) с заданной касательной в точке с абсциссой х0 требовалось найти значение производной f '(x0); второй тип: для функции, заданной аналитически, нужно было определить тангенс угла наклона касательной , проведенной к графику функции в точке с абсциссой х0. Задания первого типа верно выполнили от 18 до 60% учащихся, причем на результаты значительное влияние оказывает даже расположение касательной. Так, например, учащиеся лучше (60%) справляются с заданием, если касательная образует с положительным направлением оси абсцисс острый угол или расположена параллельно ей, значительно хуже (18%), если касательная образует тупой угол. Несколько выше результаты при выполнении второго из указанных типов заданий (от 32 до 71%). Во 2 части были представлены задания повышенной сложности на исследование свойств функции. С заданием на нахождение минимума ( максимума) функции справились от 9 до 40% учащихся. Заметим, что верно исследовали целые рациональные функции около 40% учащихся , несколько хуже справились с исследованием дробно-рациональных функций - от 12 до 25% выпускников. В работе предлагались также задания, для решения которых было необходимо провести полное исследование функции. Например, «При каком натуральном значении n уравнение х3 + 3х2 - 45х + n = 0 имеет ровно один корень?» Его выполнили от 1 до 12% выпускников, причем не приступали к нему около половины учащихся. В 3 часть каждой работы было включено одно задание на нахождение множества значений функций вида у(х) = f(g(h(x))). К выполнению этого задания в разных вариантах работы приступило от 4 до 11 % учащихся , а число решивших его составило от 2 до 4%. [6] ИЗМЕРЕНИЕ ГЕОМЕТРИЧЕСКИХ ВЕЛИЧИН. ПЛАНИМЕТРИЯ Положение центра вписанной окружности. Значительные затруднения вызвали задачи, при решении которых нужно было использовать тот факт, что центр вписанной в треугольник окружности лежит на его биссектрисе. Например, «В равнобедренный треугольник АВС с основанием АС вписана окружность с центром О. Луч СО пересекает сторону АВ в точке К, причем АК: ВК = 10:13 . Найдите длину отрезка ВМ, где М - точка пересечения медиан треугольника и АС = 20». С задачами, при решении которых требовалось применить указанный факт, справились от 2 до 14% учащихся. Свойство отрезков касательных. Значительные трудности вызвали задания, в которых требовалось применить свойство отрезков касательных. Например, «Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается стороны ВС в точке К, причем СК : ВК = 5 : 8. Найдите длину отрезка ВО, если площадь треугольника АВС равна 540». С задачами, в решении которых требовалось применить свойство отрезков касательных, справились от 3 до 1 4% учащихся. При этом 10-11% справились с задачами, при решении которых требовалось применить теорему Пифагора, подобие треугольников, свойство медианы прямоугольного треугольника. Более низкие результаты получены по тем заданиям, где применялось свойство биссектрисы треугольника или где нужно было составить уравнение. Свойства отрезков пересекающихся хорд, вписанных и центральных углов*. (Следует заметить, что свойство отрезков пересекающихся хорд - факт, который удобно применять при решении задач, но без него можно обойтись, если использовать подобие треугольников, вытекающее из свойств вписанных углов.) Невысокие результаты были показаны при выполнении заданий, в ходе решения которых требовалось использовать свойство хорд и свойства вписанных и центральных углов. Например, «Около треугольника АВС описана окружность. Медиана треугольника АМ продлена до пересечения с окружностью в точке К. Найдите сторону АС, если А М = 18, АК= 26, ВК = 10». С заданиями, где требовалось применить эти свойства, справились 2- 10% учащихся. Особо следует обратить внимание на задачи, при решении которых учащимся требовалось составить уравнение. Составление уравнений по условию геометрической задачи обычно бывает труднее для учащихся, чем просто последовательное выполнение вычислений. Но особенные трудности вызывают случаи, когда при составлении уравнения используется величина, выражающаяся в виде суммы или разности переменной с числом. Например, «Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите радиус окружности, вписанной в этот треугольник». По всем (кроме одной) задачам, в решении которых применяется такого рода «усложненное» уравнение, получены весьма низкие результаты (3-8%, для одной задачи - 14%). [6] СТЕРЕОМЕТРИЯ В целом со стереометрическими задачами справились от 2 до 31 %. Невысокие результаты показаны при выполнении тех задач, в которых существенным элементом решения я вилось применение понятия угла между плоскостями. С ними справились от 6 до 17%. Невысокие результаты (от 4 до 18%) были получены и при решении задач, где используется понятие угла между прямой и плоскостью. Лучше справились с задачами, в которых требовалось найти в кубе расстояние между скрещивающимися прямыми (от 13 до 15%) и расстояние от точки до плоскости (21%). Выпускники школы в целом продемонстрировали невысокий уровень подготовки как по курсу планиметрии, так и по курсу стереометрии. Но результаты выполнения планиметрических заданий заметно н иже результатов по стереометрическим заданиям, что объясняется рядом причин, из которых наиболее существенными, на наш взгляд, являются следующие: - курс планиметрии значительно разнообразнее по применяющимся свойствам, формулам и т.п., чем курс стереометрии, и содержит гораздо меньше задач, к которым применимы алгоритмы решения; - планиметрия не изучается в X-XI классах, и для того, чтобы успешно справиться с задачами, включенными в ЕГЭ, нужно выделить достаточное время на повторение курса планиметрии, которое не предусмотрено действующей программой. Кроме того, такое повторение должно проводиться по определенной методике, которая на сегодняшний день не создана. [6] Уроки тематического повторения вызывают у большинства учителей значительные трудности, поэтому нередко они превращаются в «натаскивание», в тренировку по решению задач, дублирующих варианты предстоящей контрольной работы. Акцент повторения нужно делать на систематизацию и обобщение знаний. Последовательность этапов урока тематического повторения: работа с таблицей; самостоятельная работа на формирование умения выбирать главные положения, на которых строится обоснование тех или иных выводов; решение содержательных (комплексных) задач; решение нестандартных задач; творческое домашнее задание. Таблицу лучше делать мелом на доске, оставив пустые места для того, чтобы учащиеся могли заполнить их необходимыми теоретическими сведениями непосредственно в ходе повторения. Специальным образом составленные таблицы не только воспроизводят на небольшой площади определенный объем информации темы в ее строго систематизированном виде, но и вызывают у учащихся потребность прокомментировать и оценить изученное. Все это делает таблицу активным рабочим средством при повторении. Самостоятельная работа, направленная на формирование у учащихся умения проводить обоснования, - важнейший этап урока повторения. К этому этапу учитель подбирает несколько задач (одношаговые, двухшаговые, реже трехшаговые) по повторяемой теме. От обычных самостоятельных работ описываемая отличается тем, что от учащихся не требуется оформлять решения в обычном смысле ( что заняло бы колоссальное время на уроке). Нужно только зафиксировать теоретический базис решения, т.е. дать перечень тех теоретических положений изученной темы, которые входят в обоснование решения задачи. По окончании самостоятельной работы целесообразно организовать ее проверку на этом же уроке (полностью или частично). [7] Конспекты уроков по 2 важным темам «Квадратные уравнения» и «Четырёхугольники». Урок систематизирующего повторения по теме «Квадратные уравнения». Работа с таблицей. На центральной части классной доски учитель делает предварительные записи к уроку в виде табл.1. (В этой таблице обведены пунктирной линией те записи, которые не должны быть на доске с самого начала урока. Они появляются по мере того, как учащиеся отвечают на соответствующие вопросы учителя.) В ходе беседы учителя с классом ответы учащихся фиксируются в таблице. Вопросы учителя по таблице 1. Таблица 1.
В каком случае уравнение вида I называется квадратным? (Ответ: в том случае, когда а≠0.) Какой вид примет это уравнение, если: b=0, c=0; b=0, c≠0 ; b≠0,c=0? Как называют такие уравнения? Имеют ли корни уравнения I1, I2, I3? (Три ученика заполняют три первые колонки в табл.1. В колонке I2 после первого «если» они пишут: «а и с имеют разные знаки», после второго «если» - а и с имеют одинаковые знаки».) Приведите примеры уравнений таких типов. (Примеры также записываются на доске.) От чего зависит наличие действительных корней уравнений? Сколько корней могут иметь квадратные уравнения? Какие формулы для нахождения корней вы знаете? (Трое учащихся записывают на доске эти формулы.) Можно ли решить неполное квадратное уравнение с помощью этих формул? Приведите пример. К какому типу относится уравнение 2х2+х-3=0? Решите его. Запишите на доске краткую формулировку теоремы Виета и обратной теоремы, а затем дайте их словесные формулировки. | ||||||||||||||||||||||||||



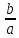



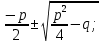
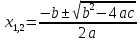 ,
,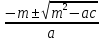
 .
.