ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов

• Название: Теория вычислительных процессов
• Анкор: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Дата: 01.04.2018
• Размер: 2.17 Mb.
• Имя файла: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Тип: Документы; #17485
• страница: 19 из 20

Анализ сетей Петри
Моделирование систем сетями Петри, прежде всего, обусловлено необходимостью проведения глубокого исследования их поведения. Для проведения такого исследования необходимы методы анализа свойств самих сетей Петри. Этот подход предполагает сведение исследования свойств реальной системы к анализу определенных свойств моделирующей сети Петри.
Свойства сетей Петри
Позиция p P сети Петри N = (P,Т,I,O) c начальной маркировкой  является k-ограниченной, если ’(p) k для любой достижимой маркировки ’ R(N,). Позиция называется ограниченной, если она является k-ограниченной для некоторого целого значения k. Сеть Петри ограниченна, если все ее позиции ограниченны.

Позиция p P сети Петри N = (P,Т,I,O) c начальной маркировкой  является безопасной, если она является 1-ограниченной. Сеть Петрибезопасна, если безопасны все позиции сети.

Сеть Петри N = (P,Т,I,O) с начальной маркировкой  является сохраняющей, если для любой достижимой маркировки ’ R(N,) справедливо следующее равенство:

.

Тупик в сети Петри – один или множество переходов, которые не могут быть запущены. Определим для сети Петри N с начальной маркировкой следующие уровни активности переходов:

Уровень 0: Переход t обладает активностью уровня 0 и называется мёртвым, если он никогда не может быть запущен.

Уровень 1: Переход t обладает активностью уровня1 и называется потенциально живым, если существует такая ’ R(N,), что t разрешён в’.

Уровень 2: Переход t, обладает активностью уровня2 и называется живым, если для всякой ’ R(N,) переход t является потенциально живым для сети Петри N с начальной маркировкой ’.

Сеть Петри называется живой, если все её переходы являются живыми.

Задача достижимости: Для данной сети Петри с маркировкой  и маркировки ’ определить: ’ R(N,)?

Задача покрываемости: Для данной сети Петри N с начальной маркировкой  и маркировки ’ определить, существует ли такая достижимая маркировка ” R(N,), что "  ’.

(Отношение "  ’ истинно, если каждый элемент маркировки " не меньше соответствующего элемента маркировки ’.)

Сети Петри присуще некоторое поведение, которое определяется множеством ее возможных последовательностей запусков переходов или ее множеством достижимых маркировок. Понятие эквивалентности сетей Петри определяется через равенство множеств достижимых маркировок.

Сеть Петри N = (P,Т,I,O) с начальной маркировкой  и сеть Петри N’ = (P’,Т’,I’,O’) с начальной маркировкой ’ эквивалентны, если справедливо R(N,) = R(N’,’).

Понятие эквивалентности сетей Петри может быть определено также через равенство множеств возможных последовательностей запусков переходов.

Более слабым, по сравнению с эквивалентностью, является свойство включения, определение которого совпадает с определением эквивалентности, с точностью до замены = на .
Методы анализа
Особый интерес вызывают методы анализа свойств сетей Петри, которые обеспечивают автоматический анализ моделируемых систем. Сначала рассмотрим метод анализа сетей Петри, который основан на использовании дерева достижимости.

Дерево достижимости

Д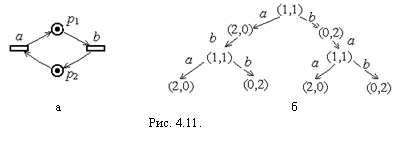ерево достижимости представляет все достижимые маркировки сети Петри, а также – все возможные последовательности запусков ее переходов.

Пример 4.4. Частичное дерево достижимости маркированной сети Петри изображено на рисунке 4.11, а, а частичное дерево достижимости для трёх шагов построения имеет вид (рис. 4.11, б).

Для сети Петри с бесконечным множеством достижимых маркировок дерево достижимости является бесконечным. Сеть Петри с конечным множеством достижимых маркировок также может иметь бесконечное дерево достижимости (см. пример 4.4). Для превращения бесконечного дерева в полезный инструмент анализа строится его конечное представление. При построении конечного дерева достижимости для обозначения бесконечного множества значений маркировки позиции используется символ . Также используются следующие ниже операции над ,определяемые для любого постоянного a.

 -- а = ;  + а = ; а < ;  .

Алгоритм построения конечного дерева достижимости. Каждая вершина дерева достижимости классифицируется алгоритмом или какграничнаявершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Алгоритм начинает работу с определения начальной маркировки корнем дерева, и граничной вершиной. Один шаг алгоритма состоит в обработке граничной вершины. Пусть х— граничная вершина, тогда её обработка заключается в следующем:

1. Если в дереве имеется другая вершина y, не являющаяся граничной, и с ней связана та же маркировка, [x]=[y], то вершина хстановится дублирующей.

2. Если для маркировки [х] ни один из переходов не разрешен, то xстановится терминальной.

3. В противном случае, для всякого перехода t T, разрешенного в [х], создаётся новая вершина z дерева достижимости. Маркировка [z],связанная с этой вершиной, определяется для каждой позиции p Pследующим образом:

3.1. Если [х](p) = , то [z](p) = .

3.2. Если на пути от корневой вершины к x существует вершина y с [y] < ’ (где ’ – маркировка, непосредственно достижимая из [х] посредством запуска перехода t) и [y](p) < ’(p), то [z](p) = . (В этом случае последовательность запусков переходов, ведущая из маркировки [y] в маркировку ’, может неограниченно повторяться и неограниченно увеличивать значение маркировки в позиции p.) В противном случае [z](p) = ’(p).

4. Строится дуга с пометкой t, направленная от вершины x к вершине z. Вершина х становится внутренней, а вершина z – граничной.

Такая обработка алгоритмом граничных вершин продолжается до тех пор, пока все вершины дерева не станут терминальными, дублирующими или внутренними. Затем алгоритм останавливается.

Важнейшим свойством алгоритма построения конечного дерева достижимости является то, что он за конечное число шагов заканчивает работу.

П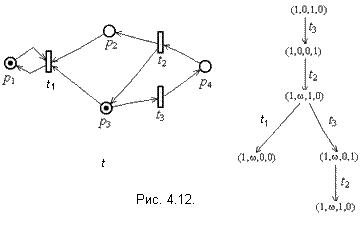ример 4.5. Конечное дерево достижимости сети Петри.

Сеть Петри и ее конечное дерево достижимости изображены на рис. 4. 12.:

Важнейшим свойством алгоритма построения конечного дерева достижимости является то, что он за конечное число шагов заканчивает работу. Доказательство основано на трёх леммах.

Лемма4.1. В любом бесконечном направленном дереве, в котором каждая вершина имеет только конечное число непосредственно последующих вершин, существует бесконечный путь, исходящий из корня.

Доказательство. Пусть x₀ корневая вершина. Поскольку имеется только конечное число непосредственно следующих за x₀ вершин, но общее число вершин в дереве бесконечно, по крайней мере, одна из непосредственно следующих за x₀ вершин должна быть корнем бесконечного поддерева. Выберем вершину x₁ непосредственно следующую за x₀ и являющуюся корнем бесконечного поддерева. Теперь одна из непосредственно следующих за ней вершин также является корнем бесконечного поддерева, выберем в качестве такой вершины x₂. Если продолжать этот процесс бесконечно, то получим бесконечный путь в дереве – x₀,x₁,x₂,…,x_n,… .

Лемма 4.2. Всякая бесконечная последовательность неотрицательных целых содержит бесконечную неубывающую последовательность.

Доказательство. Возможны два случая:

1. Если какой-либо элемент последовательности встречается бесконечно часто, то пусть x₀ является таким элементом. Тогда бесконечная подпоследовательность x₀,x₀,…,x₀,… является бесконечной неубывающей подпоследовательностью.

2. Если никакой элемент не встречается бесконечно часто, тогда каждый элемент встречается только конечное число раз. Пусть x₀ —произвольный элемент последовательности. Существует самое большее x₀ целых, неотрицательных и меньших, чем x₀ (0,..., x₀ - 1), причем каждый из них присутствует в последовательности только конечное число раз. Следовательно, продвигаясь достаточно долго по последовательности, мы должны встретить элемент x₁, x₁  x₀. Аналогично должен существовать в последовательности x₂, x₂  x₁, и т. д. Это определяет бесконечную неубывающую последовательность x₀,x₁,x₂,…,x_n,… .

Таким образом, в обоих случаях бесконечная неубывающая подпоследовательность существует.

Лемма4.3. Всякая бесконечная последовательность n-векторов над расширенными символом  неотрицательными целыми содержит бесконечную неубывающую подпоследовательность.

Доказательство. Доказываем индукцией по n, где n — размерность векторного пространства.

1. Базовый случай (n = 1). Если в последовательности имеется бесконечное число векторов вида <>, то они образуют бесконечнуюнеубывающую последовательность (так как справедливо  ). В противном случае бесконечная последовательность, образованная удалением конечного числа экземпляров <>, имеет по лемме 4.2 бесконечную неубывающую подпоследовательность.

2. Индуктивное предположение. (Допустим, что лемма верна для n докажем её справедливость для n+1.) Рассмотрим первую координату. Если существует бесконечно много векторов, имеющих. в качестве первой координаты , тогда выберем эту бесконечную подпоследовательность, которая не убывает (постоянна) по первой координате. Если только конечное число векторов имеют  в качестве первой координаты, то рассмотрим бесконечную последовательность целых, являющихся значениями первых координат. По лемме 4.2 эта последовательность имеет бесконечную неубывающую подпоследовательность. Она определяет бесконечную последовательность векторов, которые не убывают по своей первой координате.

В любом случае мы имеем последовательность векторов, неубывающих по первой координате. Применим индуктивное предположение к последовательности n-векторов, которая получается в результате отбрасывания первой компоненты n+1-векторов. Полученная бесконечная подпоследовательность является неубывающей по каждой координате.

Докажем следующую теорему.

Теорема4.1. Дерево достижимости сети Петри конечно.

Доказательство. Докажем методом от противного. Допустим, что дерево достижимости бесконечно. Тогда по лемме 4.1 (и так как число вершин, следующих за каждой вершиной в дереве, ограничено числом переходов m) в нём имеется бесконечный путь x₀,x₁,x₂,… , исходящий из корня x₀. Тогда [x₀], [x₁], [x₂],… —бесконечная последовательность n-векторов. над Nat {}, а по лемме 4.3 она имеет бесконечную неубывающую подпоследовательность [x_k0] [x_k1] [x_k2] … . Но по построению дерева достижимости [x_i][x_j] (для i j), поскольку тогда одна из вершин была бы дублирующей и не имела следующих за собой вершин. Следовательно, это бесконечная строго возрастающая последовательность [x_k0] < [x_k1] < [x_k2] …. Но по построению, так как [x_i] < [x_j] нам следовало бы заменить по крайней мере одну компоненту [x_j], не являющуюся , на  в [x_j]. Таким образом, [x_k1] имеет по крайней мере одну компоненту, являющуюся , [x_k2] имеет по крайней мере две -компоненты, а [x_kn] имеет по крайней мере n -компонент. Поскольку маркировки n-мерные, [x_kn] имеет во всех компонентах . Но тогда у [x_kn+1] не может быть больше [x_kn]. Пришли к противоречию, что доказывает теорему.
Анализ свойств сетей Петри на основе дерева достижимости

Анализ безопасности и ограниченности. Сеть Петри ограниченна тогда и только тогда, когда символ  отсутствует в ее дереве достижимости.

Присутствие символа  в дереве достижимости ([х](p) =  для некоторой вершины x и позиции p) означает, что для произвольного положительного целого k существует достижимая маркировка со значением в позиции p, большим, чемk. Это, в свою очередь, означает неограниченность позиции p, а следовательно, и самой сети Петри.

Отсутствие символа в дереве достижимости означает, что множество достижимых маркировок конечно. Следовательно, простым перебором можно найти верхнюю границу, как для каждой позиции в отдельности, так и общую верхнюю границу для всех позиций. Последнее означает ограниченность сети Петри. Если граница для всех позиций равна 1, то сеть Петри безопасна.

Анализ сохранения.Так как дерево достижимости конечно, для каждой маркировки можно вычислить сумму начальной маркировки. Если эта сумма одинакова для каждой достижимой маркировки, то сеть Петри является сохраняющей. Если суммы не равны, сеть не является сохраняющей. Если маркировка некоторой позиции совпадает с , то эта позиция должна был исключена из рассмотрения.

Анализ покрываемости.Задача покрываемости требуется для заданной маркировки ' определить, достижима ли маркировка "  '. Такая задача решается путём простого перебора вершин дерева достижимости. При этом ищется такая вершина х, что [x]  '. Если такой вершины не существует, то маркировка ' не является покрываемой. Если она найдена, то [x] определяет покрывающую маркировку для ' Если компонента маркировки [x], соответствующая некоторой позиции p совпадает с , то конкретное её значение может быть вычислено. В этом случае на пути от начальной маркировки к покрывающей маркировке имеется повторяющаяся последовательность переходов, запуск которой увеличивает значение маркировки в позиции p. Число таких повторений должно быть таким, чтобы значение маркировки в позиции p превзошло или сравнялось с '(p).

Анализ живости. Переход t сети Петри является потенциально живым, тогда и только тогда, когда он метит некоторую дугу в дереве достижимости сети.

Доказательство очевидно.

Ограниченность метода дерева достижимости. Как видно из предыдущего, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, эквивалентности. Решение этих задач ограничено существованием символа . Символ  означает потерю информации: конкретные количества фишек отбрасываются, учитывается только существование их большого числа.

Матричные уравнения.

Другой подход к анализу сетей Петри основан на матричном представлении сетей Петри и решении матричных уравнений. Альтернативным по отношению к определению сети Петри N в виде (P,T,I,O) является определение сети N в виде двух матриц D^ и D⁺, представляющих входную и выходную функции I и O. Пусть каждая из матриц D^ и D⁺ имеет m = T  строк (по одной на переход) и n = P  столбцов (по одному на позицию).

Матричный вид сети Петри N = (P,T,I,O) задаётся парой (D^,D⁺), где

D^[k,i] = ^{^}#(p_i,t_k) – кратность дуги, ведущей из позиции p_i в переход t_k;

D⁺[k,i] = #^{^}(p_i,t_k) – кратность дуги, ведущей из перехода t_k в позицию p_i,

для произвольных 1 k m, 1 i n.

Пусть e[k] — m-вектор, k-тый элемент которого равен 1, а остальные равны 0. Переход t_k, 1 k m, в маркировке  разрешен, если  e[k]_D. Результатом запуска разрешённого переходаt_k в маркировке  является маркировка ’:

’= - e[k]_D + e[k]_D+= + e[k]_D,

где D=(D⁺ - D^) — составная матрица изменений.