ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов

• Название: Теория вычислительных процессов
• Анкор: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Дата: 01.04.2018
• Размер: 2.17 Mb.
• Имя файла: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Тип: Документы; #17485
• страница: 18 из 20

Основные определения
Теоретико-множественное определение сетей Петри
Пусть мультимножество это множество, допускающее вхождение нескольких экземпляров одного и того же элемента.

СетьПетриN является четверкой N = (P,Т,I,O), где

P = {p₁,p₂,...,p_n} —конечное множество позиций, n  0;

T = {t₁, t₂,..., t_m} — конечное множество переходов, m  0;

I:TP* — входная функция, сопоставляющая переходу мультимножество его входных позиций;

О:TP* - выходная функция, сопоставляющая переходу мультимножество его выходных позиций.

Позиция pPназывается входом для перехода t  T, если p  I(t). Позицияp  Pназывается выходом для перехода t  T, если p O(t). Структурасети Петри определяется ее позициями, переходами, входной и выходной функциями.

Пример 4.1. Сеть Петри N = (P,T,I,O),

P = {p₁,p₂,p₃},

T = {t₁,t₂},

I(t₁) = {p₁,p₁,p₂}, O(t₁) = {p₃},

I(t₂) = {p₁,p₂,p₂}, O(t₂) = {p₃}.

Использование мультимножеств входных и выходных позиций перехода, а не множеств, позволяет позиции быть кратным входом и кратным выходом перехода соответственно. При этом кратность определяется числом экземпляров позиции в соответствующем мультимножестве.
Графы сетей Петри
Наиболее наглядным представлением сети Петри является её графическое представление, которое представляет собой двудольный, ориентированный мультиграф.

Граф сети Петри обладает двумя типами узлов: кружок, представляющий позицию сети Петри; и планка или прямоугольник, представляющие переход сети Петри. О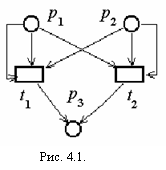риентированные дуги этого графа (стрелки) соединяют переход с его входными и выходными позициями. При этом дуги направлены от входных позиций к переходу и от перехода к выходным позициям. Кратным входным и выходным позициям перехода соответствуют кратные входные и выходные дуги. Граф сети Петри примера 4.1.

В графе сети Петри не возможны дуги между двумя позициями и между двумя переходами.

Маркировка сетей Петри
Маркировка — это размещение по позициям сети Петри фишек, изображаемых на графе сети Петри точками. Фишки используются для определения выполнения сети Петри. Количество фишек в позиции при выполнении сети Петри может изменяться от 0 до бесконечности.

Маркировка  сети Петри N= (P,T,I,О) есть функция, отображающая множество позиций P во множествоNat неотрицательных целых чисел. Маркировка , может быть также определена какn-вектор  = <(p₁), (p₂),…, (p_n)>, где n– число позиций в сети Петри и для каждого 1  i n, (p_i)  Nat – количество фишек в позиции p_i.

Маркированнаясеть Петри N = (P,Т,I,О,) определяется совокупностью структуры сети Петри (P,T,I,О) и маркировки . На рисунке 4.2 представлена маркированная сеть Петри  = <1,0,1>.

Множество всех маркировок сети Петри бесконечно. Если фишек, помещаемых в позицию слишком много, то удобнее не рисовать фишки в кружке этой позиции, а указывать их количество.
Правила выполнения сетей Петри
Сеть Петри выполняется посредством запусковпереходов. Запуск перехода управляется фишками в его входных позициях и сопровождается удалением фишек из этих позиций и добавлением новых фишек в его выходные позиции.

Переход может запускаться только в том случае, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций содержит число фишек, не меньшее, чем число дуг, ведущих из этой позиции в переход (или кратности входной дуги).

Пусть функция ^{^}#: PT  Nat для произвольных позиции p  Pи переходаtТ задает значение ^{^}#(p,t), которое совпадает с кратностью дуги, ведущей из pв t, если такая дуга существует, и с нулем, в противном случае.

Пусть функция #^{^}: TP 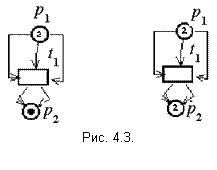 Nat для произвольных и перехода t  T позиции p  Pзадает значение #^{^}(t,p), которое совпадает с кратностью дуги, ведущей из t в p, если такая дуга существует, и с нулем, в противном случае.

Переход t  T в маркированной сети Петри N = (P,T,1,О,) разрешен, если для всех p  I(t) справедливо (p) ^{^}#(p,t).

Запуск разрешённого перехода t T из своей входной позиции p I(t) удаляет ^{^}#(p,t) фишек, а в свою выходную позицию p’ O(t) добавляет #^{^}(t,p’) фишек.

Сеть Петри до запуска перехода t₁ (рис. 4.3, а). Сеть Петри после запуска перехода t₁ (рис. 4.3, б).

Переход tв маркированной сети Петри с маркировкой  может быть запущен всякий раз, когда он разрешен и врезультате этого запуска образуется новая маркировка ', определяемая для всех p P следующим соотношением:

'(p) = (p) – ^{^}#(p,t) + #^{^}(t,p).

Запуски могут осуществляться до тех пор, пока существует хотя бы один разрешенный переход. Когда не останется ни одного разрешенного перехода, выполнение прекращается.

Если запуск произвольного перехода t преобразует маркировку  сети Петри в новую маркировку ', то будем говорить, что ' достижима из посредством запуска перехода t и обозначать этот факт, как  ^t '. Это понятие очевидным образом обобщается для случая последовательности запусков разрешённых переходов. Через R(N,) обозначим множество всех достижимых маркировок из начальной маркировки  в сети Петри N.

Преобразование маркировки сети Петри изображено на рисунке 4.3. Переход t₁ преобразует маркировку  =<5,1> в маркировку ’=<2,3>.
Моделирование систем на основе сетей Петри
В этом разделе рассмотрим метод моделирования на основе сетей Петри, а также его применение для моделирования параллельных систем взаимодействующих процессов и решения ряда классических задач из области синхронизации процессов.

События и условия

Представление системы сетью Петри основано на двух основополагающих понятиях: событияхи условиях. Возникновением событий управляет состояние системы, которое может быть описано множеством условий. Условие может принимать либо значение «истина», либо значение «ложь».

Возникновение события в системе возможно, если выполняются определённые условия – предусловиясобытия. Возникновение события может привести к выполнению других условий – постусловий события.

Пример 4.2. Моделирование последовательной обработки запросов сервером базы данных. Сервер находится в состоянии ожидания до тех пор, пока от пользователя не поступит запрос клиента, который он обрабатывает и отправляет результат такой обработки пользователю.

Условиями для рассматриваемой системы являются:

а) сервер ждет;

б) запрос поступил и ждет;

в) сервер обрабатывает запрос;

г) запрос обработан.

Событиями для этой системы являются:

1. Запрос поступил.

2. Сервер начинает обработку запроса.

3. Сервер заканчивает обработку запроса.

4. Результат обработки отправляется клиенту.

Событие	Предусловия	Постусловия
1 2 3 4	нет а, б в г	б в г, а нет

Для перечисленных событий можно составить следующую таблицу их пред- и постусловий.

Т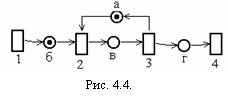акое представление системы легко моделировать сетью Петри. В сети Петри условия моделируются позициями, события —переходами. При этом входы перехода являются предусловиямисоответствующего события; выходы — постусловиями. Возникновение события моделируется запуском соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий.

На рисунке 4.4. предусловие выполняется для события 2.
Одновременность и конфликт


Особенность сетей Петри - их асинхроннаяприрода. В сетях Петри отсутствует измерение времени. В них учитывается лишь важнейшее свойство времени – частичное упорядочение событий.

Выполнение сети Петри (или поведение моделируемой системы) рассматривается здесь как последовательность дискретных событий, которая является одной из возможных. Если в какой-то момент времени разрешено более одного перехода, то любой из них может стать «следующим» запускаемым. Переходы в сети Петри, моделирующей некоторую систему, представляют ее примитивные события (длительность которых считается равной 0), и в один момент времени может быть запущен только один разрешённый переход.

М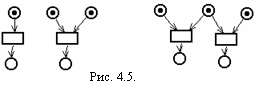оделирование одновременного (параллельного) возникновения независимых событий системы в сети Петри демонстрируется на рисунке 4.5.

В этой ситуации два перехода являются разрешенными и не влияют друг на друга в том смысле, что могут быть запущены один вслед за другим в любом порядке.

Другая ситуация в приведенной справа сети Петри. Эти два разрешённые перехода находятся в конфликте, т. е. запуск одного из них удаляет фишку из общей входной позиции и тем самым запрещает запуск другого. Таким образом, моделируются взаимоисключающие события системы.
Моделирование параллельных систем взаимодействующих процессов


Моделирование последовательных процессов

Вырожденным случаем параллельной системы процессов является система с одним процессом. Сначала рассмотрим, как сетью Петри может быть представлен отдельный процесс. Отдельный процесс описывается программой на одном из существующих языков программирования.

Пример 4.3. Последовательная программа на абстрактном языке программирования, вычисляющая Y! и произведение всех чётных чисел из отрезка [1,Y] для Y Nat.

begin

read(Y);

X1:=1;

X2:=1;

while Y>0 do

begin

if mod(Y,2) = 0

then begin

X1:=X1*Y;

end;

X2:=X2*Y;

Y:=Y-1;

end;

write(X1);

write(X2);

end

П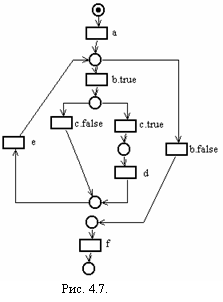рограмма представляет два различных аспекта процесса: вычисление и управление. Сети Петри удачно представляют структуру и управление программ. Они предназначены для моделирования упорядочения действий и потока информации, а не для действительного вычисления самих значений.

Стандартный способ представления структуры программы и потока управления в ней - это блок-схемы, которые в свою очередь могут быть представлены сетями Петри. Блок-схема программы состоит из узлов двух типов (принятия решения, обозначаемых ромбами, и вычисления, обозначаемых прямоугольниками) и дуг между ними. Блок-схема программы изображена на рисунке 4.6, где блоки:

a:read(Y); X1:=1; X2:=1;

b: Y>0

c: mod(Y,2)=0

d: X1:=X1*Y;

e: X2:=X2*Y; Y:=Y-1;

f: write(X1); write(X2);

В сети Петри (рисунок 4.7), моделирующей блок-схему, узлы блок-схемы представляются переходами сети Петри как показано ниже, а дуги блок-схемы — позициями сети Петри. Фишка в сети Петри представляет счетчик команд блок-схемы.

Моделирование взаимодействия процессов.

Параллельная система может строиться несколькими способами. Один из способов состоит в простом объединении процессов, без взаимодействия во время их одновременного выполнения. Так, например, если система строится этим способом из двух процессов, каждый из которых может быть представлен сетью Петри, то сеть Петри моделирующая одновременное выполнение двух процессов, является простым объединением сетей Петри для каждого из двух процессов. Начальная маркировка составной сети Петри имеет две фишки, по одной в каждой сети, представляя первоначальный счетчик команд процесса.

Такой способ введения параллелизма имеет низкое практическое значение. Далее будем рассматривать параллельные системы процессов, допускающие взаимодействие процессов во время их параллельного выполнения.

Существуют различные виды взаимодействия (синхронизации) процессов, в том числе: взаимодействие посредством общей памяти; - посредством передачи сообщения различных видов.

Таким образом, для моделирования сетями Петри параллельных систем процессов, помимо последовательных процессов, необходимо уметь моделировать различные механизмы взаимодействия (синхронизации) процессов.

Далее покажем, как сети Петри могут моделировать различные механизмы синхронизации процессов, на основе решения с помощью сетей Петри ряда задач, ставших классическими в области синхронизации.

Задача о взаимном исключении.

Пусть несколько процессов разделяют общую переменную, запись, файл или другой элемент данных. Для обновления разделяемого элементаданных процесс должен сначала считать старое значение, затем вычислить новое и, наконец, записать его на то же место. Если два процесса P₁ и P₂в одно и то же время пытаются выполнить такую последовательность действий, то могут возникнуть искажения данных. Например, возможна последовательность:

Процесс P₁ считывает значение х из разделяемого объекта;

Процесс P₂ считывает значение х из разделяемого объекта;

Процесс P₁ вычисляет новое значение х'=f(x);

Процесс P₂ вычисляет новое значение х"= g(x);

Процесс P₁ записывает х' в разделяемый объект;

Процесс P₂ записывает х" в разделяемый объект, уничтожая значение х;

Результат вычисления процесса P₁ потерян.

Д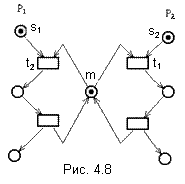ля исключения подобных проблем используется метод взаимного исключения, основанный на понятии критическая секция. Критическая секция – это участок кода процесса, на котором он осуществляет доступ к разделяемому объекту данных. Прежде, чем выполнить свою критическую секцию, процесс ждёт, пока другой процесс не закончит выполнение собственной критической секции (если такое выполнение имеет место). Затем он входит в критическую секцию и блокирует доступ для любого другого процесса к своей критической секции. После выполнения процессом критической секции деблокируется доступ для других процессов к разделяемому объекту данных.

Следующая сеть Петри (рис. 4.8) моделирует механизм взаимного исключения для двух процессов P₁ и P₂. Она легко обобщается на произвольное число процессов.

Позиция m представляет условие «критическая секция свободна», разрешающее вход в критическую секцию. Попытка процесса P₁ (P₂) войти в критическую секцию осуществляется после помещения фишки в его позицию s₁ (s₂). Такая попытка может увенчаться успехом, если в позиции mсодержится фишка. Если оба процесса пытаются войти в критическую секцию одновременно, то переходы t₁ иt₂ вступят в конфликт, и только один из них сможет запуститься. Запуск t₁ запретит запуск перехода t₂, вынуждая процесс P₂ ждать, пока процесс P₁ выйдет из своей критической секции, и возвратит фишку обратно в позицию m.

Задача о производителе/потребителе.

В 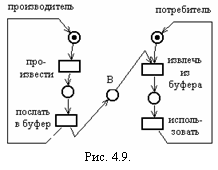задаче о производителе/потребителе также присутствует разделяемый объект – буфер, посредством которого реализуется взаимодействие через асинхронную передачу сообщений. Процесс-производитель создает сообщения, которые помещаются в буфер. Потребитель ждет, пока сообщение не будет помещено в буфер, извлекает его оттуда и использует. Такое взаимодействие может быть промоделировано сетью Петри, изображенной на рисунке. 4.9.

Позиция B представляет буфер, каждая фишка соответствует сообщению, которое произведено, но еще не использовано.

Задача об обедающих философах.

Напомним, что задача об обедающих философах была предложена Дейкстрой и связана с пятью философами, которые попеременно то гуляли по саду и думали, то ели. За едой философы сидят за круглым столом, в центре которого стояла большая миска спагетти. На столе также лежало пять вилок, по одной между соседними посадочными местами. Для употребления спагетти необходимо две вилки. Поэтому каждый философ должен сначала взять вилку слева и вилку справа, а затем приступать к еде. Возможна ситуация, в которой каждый философ возьмет вилку слева, а затем будет ждать, когда освободится вилка с правой стороны. Так они будут ждать, пока не умрут от голода. Тем самым, это состояние системы «обедающие философы» является тупиковым.

П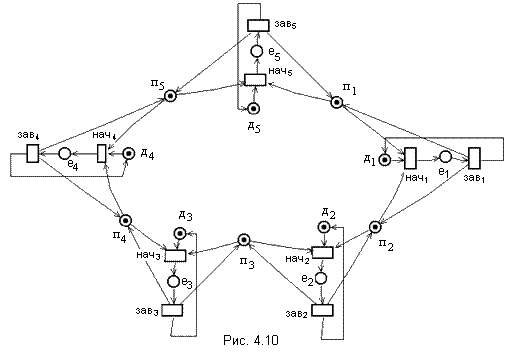роблема тупика в этой системе может быть решена путем следующей модификации ее правил поведения. Пусть философ при переходе из состояния размышления в состояние приема пищи берет одновременно обе вилки (слева и справа), если они свободны. Сеть Петри (рис. 4.10) моделирует такую модифицированную систему обедающих философов, свободную от тупиков.

В этой сети Петри позиция п_i, i {1,2,3,4,5}, представляет условие «i-тая вилка свободна». В начальной маркировке каждая из этих позиций имеет фишку. Каждому философу i {1,2,3,4,5} соответствует две позиции: позиция д_i – представляющая условие «i-тый философ думает»; и позиция е_i – представляющая условие «i-тый философ ест». В начальной маркировке все позиции д_iсодержат фишку, а все позиции е_i пусты.

Каждому философу i {1,2,3,4,5} также соответствует два перехода: переход нач_i – представляющий событие «начало приема пищи i-тым философом»; и переход зав_i – представляющий событие «завершение приема пищи i-тым философом».