ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов

• Название: Теория вычислительных процессов
• Анкор: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Дата: 01.04.2018
• Размер: 2.17 Mb.
• Имя файла: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Тип: Документы; #17485
• страница: 1 из 20

ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ

Е. В. Рабинович
ВВЕДЕНИЕ
Любая дисциплина для описания очень сложных

явлений обычно обращается к математике,

чтобы та помогла ей преодолеть эти сложности.

Программирование не является исключением.

Давид Грис

Следуя А. П. Ершову, мы употребляем термин «теоретическое программирование» в качестве названия математическойдисциплины, изучающей синтаксические и семантические свойства программ, их структуру, преобразования, процесс их составления и исполнения. Это словосочетание построено по аналогии с названиями таких наук, как теоретическая физика, теоретическая механика и т. д. В такой аналогии есть глубокий смысл: во всех случаях теоретическая научная дисциплина изучает фундаментальные понятия и законы основной науки и на основании обнаруженных закономерностей строит более частные математические модели исследуемых объектов, на которых ставит и решает прикладные задачи. В нашем случае ситуация усложняется еще тем, что объект моделирования – программа – уже представляет собой абстрактный объект.

В настоящее время сложились следующие основные направления исследований теоретического программирования.

1.Математические основы программирования. Основная цель исследований – развитие математического аппарата, ориентированного на теоретическое программирование, разработка общей теории машинных вычислений. Эта теория тесно соприкасается с теорией алгоритмов и вычислимых функций, теорией автоматов и формальных языков, логикой, алгеброй, с теорией сложности вычислений.

2.Теория схем программ. В этих работах внимание концентрируется на изучении структурных свойств и преобразований программ, а именно тех, которые отличают программы от других способов задания алгоритмов. Главным объектом исследования становится схема программы – математическая модель программы, в которой с той или иной степенью детализации отражено строение программы, взаимодействие составляющих ее компонентов.

3.Семантическая теория программ. Семантика программы или отдельных конструкций языков программирования – это их смысл, математический смысл для программиста и описание функционирования для машины. Этот раздел теоретического программирования изучает методы формального описания семантики программ, семантические методы преобразования и доказательства утверждений о программах для вычислительных машин. В частности, работы по методам проверки семантической правильности программ нацелены на автоматизацию их отладки и автоматический синтез программ.

4.Теория вычислительных процессов и структур (теория параллельных вычислений). Исследования в этой области направлены на разработку и обоснование новых методов программирования, прежде всего методов программирования параллельных процессов, взаимодействующих между собой. В частности, изучаются модели, структуры и функционирование операционных систем, методы распараллеливания алгоритмов и программ, ведется поиск новых архитектурных принципов конструирования вычислительных машин и систем на основе результатов и рекомендаций теоретического программирования и вычислительной математики.

5. Прикладные задачи теоретического программирования. Сюда в первую очередь относятся разработка и обоснование алгоритмов трансляции и алгоритмов автоматической оптимизации программ.

Две дисциплины государственного стандарта специальности 230105 – Программное обеспечение вычислительной техники и автоматизированных систем – «Теория языков программирования и методы трансляции» и «Теория вычислительных процессов» рассматривают основы теоретического программирования. Первая дисциплина охватывает первый и последний пункты нашей, не претендующей на классификационную строгость и полноту, рубрикации. Вторая дисциплина, составляющая предмет настоящего курса, раскрывает пункты 2 – 4.

Программа как формализованное описание процесса обработки данных

Целью программирования является описание процессов обработки данных (в дальнейшем - просто процессов). Данные - это представление фактов и идей в формализованном виде, пригодном для передачи и переработке в некоем процессе, а информация - это смысл, который придается данным при их представлении. Обработка данных - это выполнение систематической последовательности действий с данными. Данные представляются и хранятся на носителях данных. Совокупность носителей данных, используемых при какой-либо обработке данных, будем называть информационной средой. Набор данных, содержащихся в какой-либо момент в информационной среде, будем называть состоянием этой информационной среды. Процесс можно определить как последовательность сменяющих друг друга состояний некоторой информационной среды.

Описать процесс – значит, определить последовательность состояний заданной информационной среды. Если мы хотим, чтобы по заданному описанию требуемый процесс порождался автоматически на компьютере, необходимо, чтобы это описание было формализованным. Такое описание называется программой. С другой стороны, программа должна быть понятной и человеку, так как и при разработке программ, и при их использовании часто приходится выяснять, какой именно процесс она порождает. Поэтому программа составляется на понятном человеку формализованном языке программирования, с которого она автоматически переводится на язык соответствующего компьютера с помощью другой программы, называемой транслятором. Программисту, прежде чем составить программу, приходится проделывать большую подготовительную работу по уточнению постановки задачи, выбору метода ее решения, выяснению специфики применения требуемой программы, прояснению общей организации разрабатываемой программы и многое другое.

Правильная программа и надежная программа

Под «программой» часто понимают правильную программу, т.е. программу, не содержащую ошибок, соответствующую спецификации и дающую возможность формального вывода программы из формального набора предпосылок. Однако понятие ошибки в программе трактуется программистами неоднозначно. Будем считать, что в программе имеется ошибка, если она не выполняет того, что разумно ожидать от нее на основании документации по применению программы. Следовательно, правильнее говорить о несогласованности между программами и документацией по их применению.

В связи с тем, что задание на программу обычно формулируется не формально, а также из-за неформализованности понятия ошибки в программе, нельзя доказать формальными методами (математически) правильность программы. Нельзя доказать правильность программы и тестированием: как указал Э. Дейкстра, тестирование может лишь продемонстрировать наличие в программе ошибки.

Альтернативой правильной программы является надежная программа. Надежность программы - это ее способность безотказно выполнять определенные функции при заданных условиях в течение заданного периода времени с достаточно большой вероятностью. При этом под отказом в программе понимают проявление в нем ошибки. Таким образом, надежная программа не исключает наличия в ней ошибок - важно лишь, чтобы эти ошибки при практическом применении этой программы в заданных условиях проявлялись достаточно редко. Убедиться, что программа обладает таким свойством можно при его испытании путем тестирования, а также при практическом применении. Таким образом, фактически мы можем разрабатывать лишь надежные, а не правильные программы.

Разрабатываемая программа может обладать различной степенью надежности. Как измерять эту степень? Так же как в технике, степень надежности можно характеризовать вероятностью работы программы без отказа в течение определенного периода времени. Однако в силу специфических особенностей программ определение этой вероятности наталкивается на ряд трудностей по сравнению с решением этой задачи в технике.

При оценке степени надежности программ следует также учитывать последствия каждого отказа. Некоторые ошибки в программах могут вызывать лишь некоторые неудобства при его применении, тогда как другие ошибки могут иметь катастрофические последствия, например, угрожать человеческой жизни. Поэтому для оценки надежности программных средств иногда используют дополнительные показатели, учитывающие стоимость (вред) для пользователя каждого отказа.
СХЕМЫ ПРОГРАММ
Краткое математическое предисловие

Функции и графы

Понятие множества

Понятие множества является фундаментальным неопределяемым понятием.

Интуитивное определение множества – множество есть совокупность определенных и различных объектов (элементов).

Ведем некоторые соглашения об обозначениях элементов теории множеств и логики.

Множество мы будем задавать явным перечислением, и заключать в фигурные скобки. Например: D - множество дней недели: D = {Пн, Вт, Ср, Чт, Пт, Сб, Вс}, D₁ = {Вт, Ср, Чт, Пн, Сб, Пт, Вс}. D и D₁ эквивалентны, т.е. порядок элементов не важен.

Будем использовать обозначения: x A - x есть элемент, и принадлежит множеству A; x A - x не является элементом множества А.

Для бесконечных множеств метод перечисления элементов множества не применим, для этого используется характеристическое свойство А = {x | p(x)}, где х – переменная, значениями которой являются некоторые объекты, а р – свойство тех и только тех значений х, которые являются элементами задаваемого множества.

Пустое множество - множество, которое не содержит ни одного элемента, обозначается Ø или { }.

Если каждый элемент множества А является элементом множества В, то множество А является подмножеством множества В, будем писать A B.

Если хотя бы один элемент множества А не является элементом множества В, то множество Ане является подмножеством множества Ви это записывается А В.

Два множества А и В считают равными, если они состоят из одних и тех же элементов. Запись А = В, а А В означает неравенство множеств.

Операции над множествами

А' = {x | x A} - дополнение множества до некоторого универсального множестваU.

A B = {x | x A или x B} - объединение множеств;

A B = {x | x A и x B} - пересечение множеств;

A \ B = {x | x A, но x В} - вычитание множеств.

Свойства множеств

Для A, B и C из класса объектов U имеют место законы:

ассоциативныйзакон: (A B) C = A (B C), (A B) C = A (B C)

коммуникативныйзакон: A B = B A, A B = B A

законодополнении: A A' = U, A A' = 

законэквивалентности: A U = U, A U = A

закон о пустом множестве: A  = А, A  = 

закон инволюции: (A')' = A

закон де Моргана: (A B)' = A' B', (A B)' = A' B'

дистрибутивный закон: A (B C) = (A B)(A C),

A (B C) = (A B)(A C)

Свойства подмножеств

(рефлексивность);

и (транзитивность).

Прямое произведение множеств

Прямым (декартовым) произведением А₁ А₂ … А_n множеств А₁, А₂ … и А_nназывается множество {<a₁, a₂, …, a_n> | a₁ A₁, a₂ A₂,, a_n A_n}, а Aⁿобозначает А А … А (n раз) и называется прямой степенью множества А.

Отношения

Бинарным отношением между элементами множеств А и В называется любое подмножество R множества А В. Вместо <x, y> R часто пишут xRy.

Областью определения бинарного отношения R называется множество

_R = {x | существует y такое, что <x, y> R}.

Областью значений бинарного отношения R называется множество

_R = {x | существует y такое, что <y, x> R}.

Обратным отношением для бинарного отношения R называется множество

R^-1 = {<x, y> | <y, x> R}.

Образом множества Х относительно R называется множество

R(X) = {y | существует х Х такое, что <x, y> R},

прообразом Х относительно R называется R^-1(X).

Произведением подмножеств R₁ А В и R₂ B C называется отношение

R₁R₂ = {<x, y> | существует z такое, что <x, z> R₁, <z, y> R₂}.

Свойства отношений

Бинарное отношение R на множестве А называется

• 
  рефлексивным, если <x, х> R для всех x А;
  
• 
  симметричным, если <x, у> R <y, x> R;
  
• 
  антисимметричным, если <x, у> R и <y, x> R х = у;
  
• 
  транзитивным, если <x, у> R и <y, z> R <x, z> R.
  

Рефлексивное, симметричное и транзитивное отношение на множестве А называется эквивалентностью на А. Классом эквивалентности (смежным классом) элемента х по эквивалентности R называется множество

[x]_R= x / R = {y | <x, у> R}.

Множество классов эквивалентности элементов множества А по эквивалентности R называется фактор-множеством А по R и обозначается А / R.

Бинарное отношение на множестве А называется предпорядком на А, если оно рефлексивно и транзитивно. Рефлексивное, антисимметричное, транзитивное отношение на множестве А называется частичным порядком на А ().

Частичный порядок на множестве А называется полным на А, если каждое непустое подмножество А имеет наименьший элемент. Тогда А называется вполне упорядоченным.

Функции

Отношение f называется функцией из А в В (из А на В), если _f = A, _f В(_f = В) и для всех x, y₁, y₂ из <x, y₁> f и <x, y₂> f следует y₁ = y₂. Обозначение f: A B. Пишем y = f(x) вместо <x, y> f и называем y значением функции f при значении аргумента х.

Функция f: A Bосуществляет взаимно однозначное соответствие межу А и В, если _f= A, _f= В и из того, что y = f(x₁), y = f(x₂) следует х₁ = х₂.

Пусть А и В – частично упорядоченные множества и f– функция из А в В. f называется монотонным отображением, если из х₁ х₂ следует f(x₁) f(x₂) для всехx₁, x₂ А.

Функцию f: X Y называют n-местной функцией над множеством А, если Y = A и X = Aⁿ.

Предикатом называют функцию, областью значений которой является множество символов-цифр {0, 1}. При этом говорят, что предикат P: X {0, 1} истинен для x X, если P(x) = 1, и ложен, если P(x) = 0. Отношение на множестве Х – это двухместный предикат P: X² {0, 1}.

Алфавитом называют непустое конечное множество символов. Например, V₁ = {a, b}, V₂ = {0, 1}, V₃ = {a, +, 1, =} – алфавиты. Словом в алфавите V называется конечный объект, получаемый выписыванием одного за другим символов V, например, а + 1 = 1 + а – слово в алфавите V₃, 101011 – слово в алфавите V₂, abaab – слово в алфавите V₁. Длина слова – число символов в нем, пустое слово не содержит ни одного символа.

Множество всех слов в алфавите V обозначается V^*.

n-местной словарной функцией над алфавитом V называют n-местную функцию над V^*, т. е. функцию из V^* V^* … V^* (n раз) в V^*.
Понятие графа

Направленным графом называется тройка G = (V, E, Ф), где V - множество вершин, Е – множество дуг, а Ф – функция из Е в (V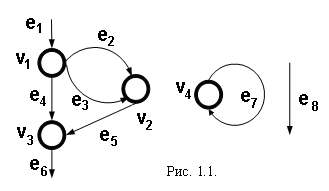{})²,  V. Дуга е называется входом графа, если Ф(е) = (, ), для  V{}; внутренней, если Ф(е) = (₁, ₂) для ₁,₂ V; выходом, если Ф(е) = (,), для  V{}. Дуга е, являющаяся одновременно и входом и выходом графа, называется висячей; для нее Ф(е) = (,). Дуги, не являющиеся внутренними, называются также свободными.

Говорят, что дуга е инцидентна вершине , если е выходит из  или ведет в . Две дуги смежны, если существует хотя бы одна инцидентная им обеим вершина. Вершина  называется наследником вершины ', если в графе имеется хотя бы одна такая дуга, что Ф(е) = (', ).

Изображенный на рисунке 1.1. граф G₁ содержит 4 вершины, 8 дуг. Дуга е₁ – входная, дуга е₆ – выходная, дуга е₈ – висячая, остальные дуги внутренние; вершины ₁ и ₃ наследники вершины ₁.

Путем в графе G называется последовательность …_ie_i_i+1… дуг и вершин, такая, что для всех i Ф(е_i) = (_i,_i+1). Образом пути называется слово, составленное из пометок проходимых дуг и вершин.

Две вершины ₁,₂ графа G называются связанными, если ₁ = ₂ или существует маршрут е₁, …, е_n графа G такой, что дуга е₁ инцидентна вершине ₁, а дуга е_n – вершине ₂.