ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов

• Название: Теория вычислительных процессов
• Анкор: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Дата: 01.04.2018
• Размер: 2.17 Mb.
• Имя файла: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Тип: Документы; #17485
• страница: 3 из 20

Линейная форма стандартной схемы
Для использования линейной формы СПП множество специальных символов расширим дополнительными символами :, goto, if, then, else. СПП в линейной форме представляет собой последовательность инструкций, которая строится следующим образом:

1.если выходная дуга начальной вершины с оператором start(х₁,..., х_n) ведет к вершине с меткой L, то начальной вершине соответствует инструкция:

0: start(х₁,..., х_n) goto L;

2.если вершина схемы S с меткой L - преобразователь с оператором присваивания х:=τ, выходная дуга которого ведет к вершине с меткой L1, то этому преобразователю соответствует инструкция:

L: x:= τ goto L1;

3.если вершина с меткой L - заключительная вершина с оператором stop(τ₁,...τ_m), то ей соответствует инструкция:

L: stop(τ₁,..., τ_m);

4.если вершина с меткой L - распознаватель с условием р(τ₁,...τ_k), причем 1-дуга ведет к вершине с меткой L1, а 0-дуга - к вершине с меткой L0, то этому распознавателю соответствует инструкция:

L: ifр(τ₁,...τ_k) thenL1 else L0;

5.если вершина с меткой L - петля, то ей соответствует инструкция:

L: loop.

Обычно используется сокращенная запись (опускание меток). Полная и сокращенная линейные формы ССП (рисунок 1.3, а) приведены ниже

0:start(х) goto 1,start(х),

1:у:=а goto 2, у:=а,

2:ifр(х) then 5 else 3,2:ifр(х) then 5 else 3,

3:у:=g(x,y) goto 4,3:у:=g(x,y),

4:х:=h(x) goto 2,х:=h(x) goto 2,

5:stop(у).5:stop(у).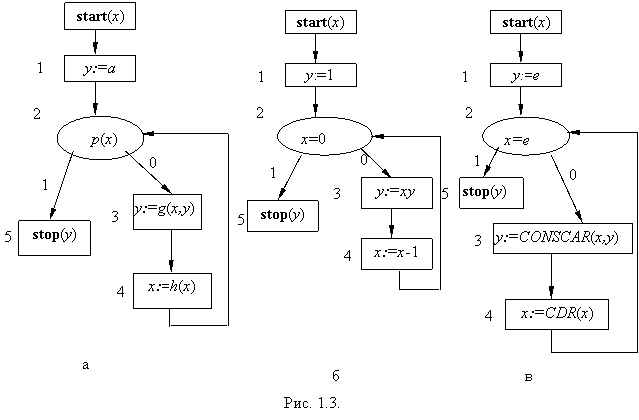


Интерпретация стандартных схем программ
ССП не является записью алгоритма, поэтому позволяет исследовать только структурные свойства программ, но не семантику вычислений. При построении «семантической» теории схем программ вводится понятие интерпретация ССП. Определим это понятие.

Пусть в некотором базисе В определен класс ССП. Интерпретацией базиса В в области интерпретации D называется функция I, которая сопоставляет:

1.каждой переменной х из базиса В - некоторый элемент d = I(x) из области интерпретации D;

2.каждой константе а из базиса В - некоторый элемент d = I(а) из области интерпретации D;

3.каждому функциональному символу f⁽ⁿ⁾ - всюду определенную функцию F⁽ⁿ⁾ = I(f ⁽ⁿ⁾);

4.каждой логической константе р⁽⁰⁾ - один символ множества {0,1};

5.каждому предикатному символу р⁽ⁿ⁾ - всюду определенный предикатP⁽ⁿ⁾= I(p⁽ⁿ⁾).

Пара (S,I) называется интерпретированной стандартной схемой (ИСС), или стандартной программой (СП).

Определим понятие выполнения программы.

Состоянием памяти программы (S,I) называют функцию W: X_S D, которая каждой переменной x из памяти схемы S сопоставляет элемент W(x) из области интерпретации D.

Значение терма τ при интерпретации I и состоянии памяти W (обозначим τ_I(W)) определяется следующим образом:

1) если τ = х, x – переменная, то τ_I(W) = W(x);

2) если τ = a, a – константа, то τ_I(W) = I(a);

3) если τ = f⁽ⁿ⁾(τ₁, τ₂..., τ_n), то τ_I(W) = I(f⁽ⁿ⁾)(τ_1I(W), τ_2I(W),..., τ_nI(W)).

Аналогично определяется значение теста  при интерпретации I и состоянии памяти W или _I(W):

если  = р⁽ⁿ⁾(τ₁, τ₂,..., τ_n), то _I(W) = I(p⁽ⁿ⁾)(τ_1I(W), τ_2I(W),... τ_nI(W)), n ≥ 0.

Конфигурацией программы называют пару U = (L,W), где L - метка вершины схемы S, а W - состояние ее памяти. Выполнение программы описывается конечной или бесконечной последовательностей конфигураций, которую называют протоколом выполнения программы (ПВП).

Протокол (U₀, U₁,..., U_i, U_i+1,...) выполнения программы (S,I) определяем следующим образом (ниже k_iозначает метку вершины, а W_i - состояние памяти в i-й конфигурации протокола, U_i= (k_i,W_i)): U₀= (0, W₀), W₀– начальное состояние памяти схемы S при интерпретации I.

Пусть U_i= (k_i, W_i) - i-я конфигурация ПВП, а О - оператор схемы S в вершине с меткой k_i. Если О - заключительный оператор stop(τ₁, τ₂... τ_n), то U_i- последняя конфигурация, так что протокол конечен. В этом случае считают, что, программа (S,I) останавливается, а последовательность значений τ_1I(W), τ_2I(W),..., τ_nI(W) объявляют результатом val(S,I) выполнения программы (S,I). В противном случае, т. е. когда О - не заключительный оператор, в протоколе имеется следующая, (i+1)-я конфигурация U_i+1 = (k_i+1, W_i+1), причем

а) если О - начальный оператор, а выходящая из него дуга ведет к вершине с меткой L, то k_i+1 = L и W_i+1 = W_i;

б) если О - оператор присваивания х:= τ, а выходящая из него дуга ведет к вершине с меткой L, то k_i+1 = L, W_i+1 = W_i, W_i+1(х) = τ₁(W_i);

в) если О - условный оператор  и _I(W_i) = Δ, где Δ 0,1, а выходящая из него дуга ведет к вершине с меткой L, то k_i+1 = L и W_i+1 = W_i;

г) если О - оператор петли, то k_i+1 = L и W_i+1 = W_i, так что протокол бесконечен.

Таким образом, программа останавливается тогда и только тогда, когда протокол ее выполнения конечен. В противном случае программа зацикливается и результат ее выполнения не определен.

Рассмотрим две интерпретации СПП S₁ (рисунок 1.2, а). Интерпретация(S₁, I₁) задана так:

1.область интерпретации D₁ Nat - подмножество множества Nat целых неотрицательных чисел;

2.I₁(x)=4; I₁(y)=0; I₁(a)=1;

3.I₁(g)=G, где G - функция умножения чисел, т. е. G(d1,d2)= d1*d2;

4.I₁(h)=H, где H - функция вычитания единицы, т. е. H(d)= d - 1;

5.I₁(p)=P₁, где P₁ - предикат «равно 0», т.е. P₁(d)=1, если d=0.

Программа (S₁, I₁) вычисляет 4! (рисунок 1.3, б).

Интерпретация (S₁, I₂) задана следующим образом:

1.область интерпретации D₂=V*, где V = a, b, c, V* - множество всех возможных слов в алфавите V.

2.I₂(x)=abc;

3.I₂(y)=, где  - пустое слово;

4.I₂(a)= ;

5.I₂(g)=CONSTAR;

6.I₂(h)=CDR;

7.I₂(p)=P₂, где P₂ - предикат «равное », т.е. P₂()=1, если =.

Программа (S₁, I₂) преобразует слово abc в слово cba (рисунок 1.3, в).

ПВП (S₁, I₁) и (S₁, I₂) конечен, результат - 24 и - cba (таблица 1.1 и 1.2).

Табл. 1.1.

Конфигурация		U0	U1	U2	U3	U4	U5	U6	U7	U8	U9	U10	U11	U12	U13
Метка		0	1	2	3	4	2	3	4	2	3	4	2	3
Значения	х	4	4	4	4	3	3	3	2	2	2	1	1	1	0
	у	0	1	1	4	4	4	12	12	12	24	24	24	24	24

Табл. 1.2.

Конфигурация

U0

U1

U2

U3

U4

U5

U6

U7

U8

U9

U10

U11

U12

Метка

0

1

2

3

4

2

3

4

2

3

4

2

5

Значения

x

abc

abc

abc

abc

bc

bc

bc

c

c

c







у







a

a

a

ba

ba

ba

cba

cba

cba

cba

Эквивалентность, тотальность, пустота, свобода
ССП S в базисе В тотальна (пуста), если для любой интерпретации I базиса В программа (S, I) останавливается (зацикливается).

Стандартные схемы S₁, S₂ в базисе В функционально эквивалентны (S₁  S₂), если либо обе зацикливаются, либо обе останавливаются с одинаковым результатом, т. е. val(S₁, I)  val(S₂, I).

Примеры тотальных, пустых и эквивалентных схем S₂, S₃, S₄, S₅приведены на рисунке 1.4.

Цепочкой стандартной схемы (ЦСС) называют:

1. конечный путь по вершинам схемы, ведущий от начальной вершины к заключительной;

2. бесконечный путь по вершинам, начинающийся начальной вершиной схемы.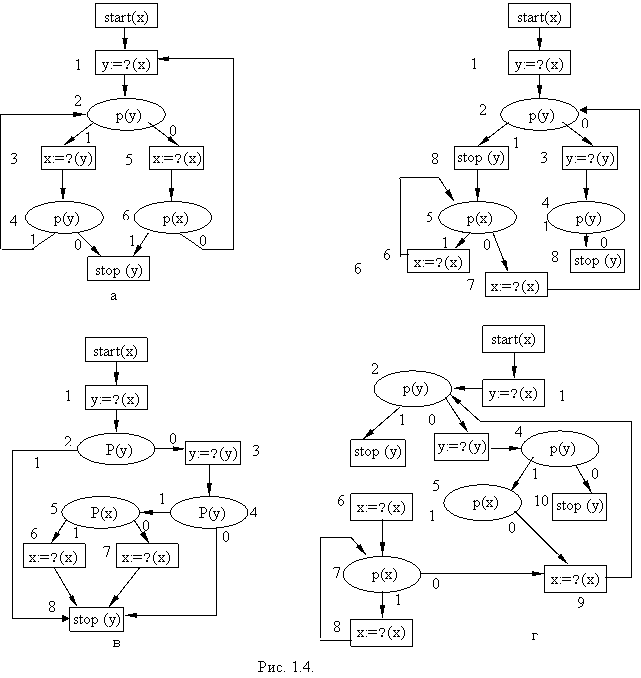



В случае, когда вершина-распознаватель (v), то дополнительно указывается верхний индекс (1 или 0), определяющий 1-дугу или 0-дугу, исходящую из вершины.

Примеры цепочек схемы S₁ (рисунок 1.3,а): (0, 1, 2¹, 5); (0, 1, 2⁰, 3, 4, 2⁰ 3, 4, 2¹, 5) и т. д.

Цепочкой операторов (ЦО) называется последовательность операторов, метящих вершины некоторой цепочки схемы.

Например для S₁: (start(х), у:=a, р¹(x), stop(у)) или (start(х), у:=a, р⁰(x), y:=g(x, y), x:=h(x), р⁰(x), y:=g(x, y), x:=h(x), р⁰(x), y:=g(x, y), x:=h(x), …)) и т. д.

Предикатные символы ЦО обозначаются так же, как вершины распознавателей в ЦСС.

Пусть S - ССП в базисе В, I - некоторая его интерпретация, (0, 1, …, l₂, l₃,…) - последовательность меток инструкций S, выписанных в том порядке, в котором эти метки входят в конфигурации протокола выполнения программы (S, I). Ясно, что эта последовательность – цепочка схемы S. Считают, что интерпретация I подтверждает (порождает) эту цепочку.

ЦСС в базисе В называют допустимой, если она подтверждается хотя бы одной интерпретацией этого базиса.

Не всякая ЦСС является допустимой. В схеме S₂(рисунок 1.4,а) цепочки(0, 1, 2⁰, 5, 6¹, 7), (0, 1, 2¹, 3, 4⁰, 7) и все другие конечные цепочки не подтверждаются ни одной интерпретацией.

Свойство допустимости цепочек играет чрезвычайно важную роль в анализе ССП. В частности оно определяет те случаи, когда стандартная схема свободна.

ССП свободна, если все ее цепочки допустимы.

Допустимая цепочка операторов - это цепочка операторов, соответствующая допустимой цепочке схемы. В тотальной схеме все допустимые цепочки (и допустимые цепочки операторов) конечны. В пустой схеме - бесконечны.

Рассмотренные свойства распространяются на все другие классы стандартных схем и образуют опорные пункты схематологии программирования.