ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов
 Скачать 2.17 Mb.
|
|
Свободные интерпретации Множество всех интерпретаций очень велико и поэтому вводится класс свободных интерпретаций (СИ), который образует ядро класса всех интерпретаций в том смысле, что справедливость высказываний о семантических свойствах ССП достаточно продемонстрировать для программ, получаемых только с помощью СИ. Все СИ базиса В имеют одну и ту же область интерпретации, которая совпадает со множеством Т всех термов базиса В. Все СИ одинаково интерпретируют переменные и функциональные символы, а именно: а) для любой переменной х из базиса В и для любой СИ Ih этого базиса Ih(x) = x; б) для любой константы a из базиса ВIh(a) = a; в) для любого функционального символа f(n) из базиса В, Ih(f(n)) = F(n): Tn  T, где F(n) - словарная функция такая, что F(n)(1, 2, ..., n) = f(n) (1, 2, ..., n), n 1, т. е. функция F(n) по термам 1, 2, ..., n из Т строит новый терм, используя функциональный смысл символа f(n).Интерпретация предикатных символов полностью свободна, т.е. разные СИ различаются лишь интерпретаций предикатных символов. Таким образом, после введения СИ термы используются в двух разных качествах, как функциональные выражения в схемах и как значения переменных и выражений. В дальнейшем термы-значения будем заключать в апострофы. Например, если где 1=`f(x,a)` - терм-значение переменной x, а где 2 = `g(y)` - терм-значение переменной y, то значение свободно интерпретированного терма 3=f(x, h(y)) равно терму-значению `f(f(x,a), h(g(y)))`. Пример 1.1. Пусть Ih -СИ базиса, в котором определена схема S1 (рисунок 1.3, а), и в этой интерпретации предикат Р = Ih(р) задан так: P() = 1, если число функциональных символов в больше двух; P() = 0, в противном случае. Тогда ПВП (S1,Ih) можно представить таблицей 1.3. Табл. 1.3.
Обратим внимание на следующую особенность термов. Если из терма удалить все скобки и запятые, то получим слово (назовем его бесскобочным термом), по которому можно однозначно восстановить первоначальный вид терма (при условии, что отмечена или известна местность функциональных символов). Например, терму g(2)(h(1)(x), g(2)(x,y)) соответствует бесскобочный терм ghxgxy. Правила восстановления терма по бесскобочной записи аналогичны правилам восстановления арифметических по их прямой польской записи, которая просто и точно указывает порядок выполнения операций. В этой записи, впервые примененной польским логиком Я. Лукашевичем, операторы следуют непосредственно за операндами. Поэтому ее иногда называют постфиксной записью. Классическая форма записи, как мы обычно пишем, называется инфиксной. Например: A*B => AB*; A*(B+C/D) =>ABCD/+*; A*B+C =>AB*C+;A*B+C*D =>AB*CD*+. Правила представления в польской записи: 1) Идентификаторы следуют в том же порядке, что и в инфиксной записи; 2) Операторы следуют в том же порядке, в каком они должны вычисляться (слева направо); 3) Операторы располагаются непосредственно за своими операндами. Бесскобочная запись термов короче и она будет использоваться далее наряду с обычной записью. Согласованные свободные интерпретации Полагают, что интерпретация I и СИ Ih (того же базиса В) согласованы, если для любого логического выражения справедливо Ih() = I(). Пусть, например, = `g(h(h(x)),g(h(x),g(x,a)))`, а интерпретация I3 совпадает с интерпретацией I1из п. 1.2.4 за исключением лишь того, что I(x) = 3. Так как I3(a) = 1; I3(g) - функция умножения; I3(h) - функция вычитания 1; получаемI3() = ((3-1)-1)*((3-1)*(3*1)) = 6. В этом случае Ihпримера из п. 1.3.2. согласована с только что рассмотренной интерпретацией I3, а так же с I2 (рисок 1.3, в), но не согласована с I1 (рисунок 1.3, б). Справедливы прямое и обратное утверждения, что для каждой интерпретации I базиса В существует согласованная с ней СИ этого базиса. Так, например, выше было сказано, что Ih рассмотренного примера не согласована с I1. Что бы сделать Ih согласованной, необходимо условие Р() видоизменить: P() = 1, если число функциональных символов в больше трех, P() = 0, в противном случае. Можно поступить и по другому. Оставить Ih без изменения и согласовать с ней I1. Для этого необходимо будет заменить I1(x) = 4, на I1(x) = 3. Введем важное вспомогательное понятие подстановки термов, используемое в дальнейшем. Если x1, …, xn (n ≥ 0) – попарно различные переменные, 1, ..., n – термы из Т, а - функциональное или логическое выражение, то через [1/x1, ..., n /xn] будем обозначать выражение, получающееся из выражения одновременной заменой каждого из вхождений переменной xi на терм I (i = 1, …, n). Например: a[y/x] = a, f(x, y)[y/x, x/y] = f(y, x), g(x)[g(x)/x] = g(g(x)), p(x)[a/x] = p(a). Приведем без доказательства несколько важных утверждений: Если интерпретация I и свободная интерпретация Ih согласованы, то программы (S, I) и (S, Ih) либо зацикливаются, либо обе останавливаются и I(val(S,Ih)) = val(S,I), т.е. каждой конкретной программе можно поставить во взаимно-однозначное соответствие свободно интерпретированную (стандартную) согласованную программу. Если интерпретация и свободная интерпретация согласованы, они порождают одну и ту же цепочку операторов схемы. Теорема Лакхэма – Парка – Паттерсона. Стандартные схемы S1 и S2 в базисе В функционально эквивалентны тогда и только тогда, когда они функционально эквивалентны на множестве всех свободных интерпретаций базиса В, т.е. когда для любой свободной интерпретации Ihпрограммы (S1,Ih) и (S2,Ih) либо обе зацикливаются, либо обе останавливаются и val(S1,I) = {I(val(S1 Ih)) = I(val(S2 Ih))} = val(S2,I). Стандартная схема S в базисе В пуста (тотальна, свободна) тогда и только тогда, когда она пуста (тотальна, свободна) на множестве всех свободных интерпретаций этого базиса, т.е. если для любой свободной интерпретации Ih программа (S, Ih) зацикливается (останавливается). Стандартная схема S в базисе В свободна тогда и только тогда, когда она свободна на множестве всех свободных интерпретаций базиса В, т. е. когда каждая цепочка схемы подтверждается хотя бы одной свободной интерпретацией. Логико-термальная эквивалентность Отношение эквивалентности Е, заданное на парах стандартных схем, называют корректным, если для любой пары схем S1 и S2 из S1Е S2 следует, что S1 S2, т. е. S1 и S2 функционально эквивалентны. Поиск разрешимых корректных отношений эквивалентности представляет значительный интерес с точки зрения практической оптимизации преобразования программ, поскольку в общем виде функциональная эквивалентность стандартных схем алгоритмически неразрешима. Идея построения таких (корректных и разрешимых) отношений связанна с введением понятия истории цепочки схем. В истории с той или иной степенью детальности фиксируются промежуточные результаты выполнения операторов рассматриваемой цепочки. Эквивалентными объявляются схемы, у которых совпадают множества историй всех конечных цепочек. Одним из отношений эквивалентности является логико-термальная эквивалентность (ЛТЭ). Определим термальное значение переменной х для конечного пути w схемы S как терм t(w, x), который строится следующим образом. 1.Если путь w содержит только один оператор А, то: t(w, x) = , если А – оператор присваивания, t(w, x) = х, в остальных случаях. 2.Если w = w’Ае, где А – оператор, е – выходящая из него дуга, w’ – непустой путь, ведущий к А, а x1, …, xn – все переменные терма t(Ае, x), то t(w, x) = t(Ае, x)[t(w’, x1)/x1, …, t(w’, xn)/xn]. Понятие термального значения распространим на произвольные термы : t(w, x) = [t(w, x1)/x1, …, t(w, xn)/xn]. Например, пути start(х); y:=x; p1(x); x:=f(x); p0(y); y:=x; p1(x); x:=f(x) в схеме на рисунке 1.5, а соответствует термальное значение f(f(x)) переменной х. Для пути w в стандартной схеме S определим ее логико-термальную историю (ЛТИ) lt(S, w) как слово, которое строится следующим образом. 1.Если путь w не содержит распознавателей и заключительной вершины, то lt(S, w) – пустое слово. 2.Если w = w’vе, где v – распознаватель с тестом p(1, ..., k), а е – выходящая из него Δ-дуга, Δ  0,1, то lt(S, w) = lt(S, w’) pΔ(t(w’, 1), …, t(w’, k)). 3.Если w = w’v, где v – заключительная вершина с оператором stop(1, ..., k), то lt(S, w) = lt(S, w’) t(w’, 1) … t(w’, k). Например, логико-термальной историей пути, упомянутого в приведенном выше примере, будет p1(x) p0(x) p1(f(x)). Детерминантом (обозначение: det(S)) стандартной схемы S называют множество ЛТИ всех ее цепочек, завершающихся заключительным оператором. Схемы S1 и S2называют ЛТЭ (лт - эквивалентными) S1 ЛТ S2, если их детерминанты совпадают. 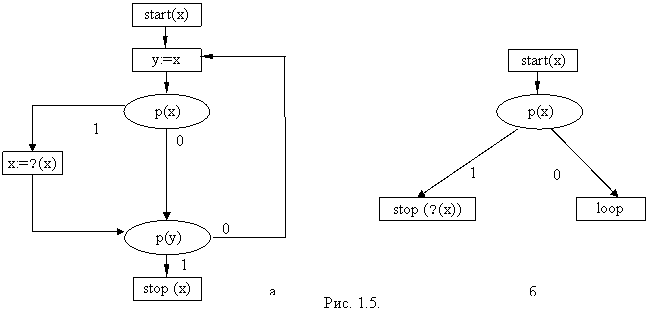 Приведем без доказательства следующие утверждение:Логико-терминальная эквивалентность корректна, т. е. из ЛТЭ следует функциональная эквивалентность (S1 ЛТ S2  S1 S2). Обратное утверждение как видно из рисунка 1.5 не верно. ЛТ – эквивалентность допускает меньше сохраняющих ее преобразований, чем функциональная эквивалентность. Моделирование стандартных схем программ Одноленточные автоматы Конечный одноленточный (детерминированный, односторонний) автомат обнаруживают ряд полезных качеств, используемых в теории схем программ для установления разрешимости свойств ССП. Одноленточный конечный автомат (ОКА) над алфавитом V задается набором: A = {V, Q, R, q0, #, I} и правилом функционирования, общим для всех таких автоматов. В наборе А: V - алфавит; Q - конечное непустое множество состояний (Q  V=);R - множество выделенных заключительных состояний (R  Q);q0 - выделенное начальное состояние; I - программа автомата; # - «пустой» символ. П 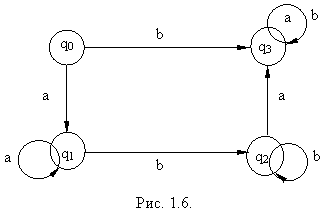 рограмма автомата I представляет собой множество команд вида qаq', в которой q,q' Q, a V и для любой пары (q, a) существует единственная команда, начинающаяся этими символами. Неформально ОКА можно представить как абстрактную машину, похожую на машину Тьюринга, но имеющую следующие особенности: 1) выделены заключительные состояния; 2) машина считывает символы с ленты, ничего не записывая на нее; 3) на каждом шаге головка автомата, считав символ с ленты и перейдя согласно программе в новое состояние, обязательно передвигается вправо на одну клетку; 4) автомат останавливается в том и только в том случае, когда головка достигнет конца слова, т.е. символа . Говорят, что автомат допускает слово в алфавите V, если, начав работать с лентой, содержащей это слово, он останавливается в заключительном состоянии. Автомат A задает характеристическую функцию множества MA допускаемых им слов в алфавите V, т. е. он распознает, принадлежит ли заданное слово множеству MA если связать с остановкой в заключительном состоянии символ 1, а с остановкой в незаключительном состоянии – 0. Наглядным способом задания ОКА служат графы автоматов. Автомат А представляется графом, множество вершин которого – множество состояний Q, и из вершины q в вершину q’ ведет дуга, помеченная символом а, тогда и только тогда, когда программа автомата содержит командуqа q'. Работе автомата над заданным словом соответствует путь из начальной вершины q. Последовательность проходимых вершин этого пути – это последовательность принимаемых автоматом состояний, образ пути по дугам – читаемое слово. Любой путь в графе автомата, начинающийся в вершине q0 и заканчивающийся в вершине q R, порождает слово, допустимое автоматом.Пример 1.2. ОКА A = ({a, b}, {q0, q1, q2, q3}, {q2}, q0, , I), допускающего слова {an bm | n = 1,2, ...; m = 1,2, ...}, задается графом (рисунок 1.6.). Программа I содержит команды: q0a q1; q0bq3; q1aq1; q1bq2; q2aq3; q2bq2; q3aq3; q3bq3.Автомат называется пустым, если МА = , Автоматы А1 и А2 эквивалентны, если МА1 = МА2. Для машины Тьюринга проблемы пустоты и эквивалентности неразрешимы, более того, они не являются частично разрешимыми. Ситуация меняется для конечных автоматов. Для ОКА доказано: 1) Проблема пустоты ОКА разрешима. Доказательство основано на проверке допустимости конечного множества всех слов, длина которых не превышает числа состояний ОКА - n. Если ни одно слово из этого множества не допускается, то ОКА «пуст». 2) Предположение о том, что минимальная длина допускаемого слова больше n отвергается на том основании, что оно может быть сведено к слову меньшей длины, путем выбрасывания участков между двумя повторяющимися в пути узлами. 3) Проблема эквивалентности ОКА разрешима. Доказательство основано на использовании отношения эквивалентности двух состояний q и q': если состояния q и q' эквивалентны, то для всех a A состояния (q, a) и '(q', a) также эквивалентны. Формируемые пары не должны входить одновременно заключительное и незаключительное состояния. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||