ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов

• Название: Теория вычислительных процессов
• Анкор: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Дата: 01.04.2018
• Размер: 2.17 Mb.
• Имя файла: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Тип: Документы; #17485
• страница: 2 из 20

Вычислимость и разрешимость
Данное в п. 1.1.1. определение функции не содержит указаний о том, как для заданных значений аргументов получить соответствующие значения функции. Было бы практичнее переформулировать это определение таким образом, чтобы оно содержало конструктивную процедуру, или алгоритм, нахождения значений функции. Однако такое определение уже приведенного выше, т. е. определяет лишь некоторый подкласс функций, которые называют вычислимыми функциями.

Тьюринг в середине 30-х годов формализовал способ получения значений вычислимой функции с помощью абстрактной «математической машины», вычисляющей значения функции по значениям ее аргументов. Конкретная машина Тьюринга задает конкретную вычислимую функцию и его гипотеза (тезис) состояла в том, что каждая функция, для которой существует алгоритм нахождения ее значений, представима некоторой машиной Тьюринга, т. е. является вычислимой. Тезис Тьюринга не может быть доказан, так как наряду с формальным понятием вычислимой функции он содержит эмпирическое понятие алгоритма. Однако интуиция, отсутствие опровергающих примеров и равносильность различных формализаций вычислимости убеждают в справедливости этого тезиса.

Машина Тьюринга Т задает словарную функцию над некоторым алфавитом V и представляет собой описание машины — набор (F, Q, q₀, #, I) - и правило функционирования, общее для всех машин, где

V — алфавит машины;

Q — конечное непустое множество символов, называемых состояниями машины (Q V = );

q₀ — выделенный элемент множества Q, называемый начальным состоянием;

# — специальный «пустой» символ, не принадлежащий ни V, ни Q;

I — программа машины.

Программа машины — это конечное множество слов вида qa q'a'd, называемых командами, где q, q' Q, a, a' V {#}; — вспомогательный символ-разделитель; d — элемент множества {l, r, р}, содержащего три специальных символа, которых нет ни в V, ни в Q. Предполагается также, что в программе I никакие две команды не могут иметь одинаковую пару первых двух символов.

Правило функционирования поясним неформально на распространенной «физической» модели машины Тьюринга. Машина состоит из потенциально бесконечной (в обе стороны) ленты, управления и головки, перемещаемой вдоль ленты (см. рисунок 1.2.). Лента разбита на клетки, которые могут содержать символы из алфавита V или быть пустыми, т. е. содержать символ #. Управление на каждом шаге работы машины находится в одном из состояний из Q, расшифровывает программу, которая однозначно определяет поведение машины и управляет головкой.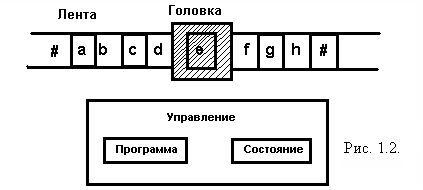



Головка в каждый момент расположена против некоторой клетки ленты и может считывать символы с ленты, записывать их на ленту и перемещаться в обе стороны вдоль ленты. Машина функционирует следующим образом. В начальный момент на ленте записано некоторое слово из V, а управление находится в начальном состоянии q₀. Начальное слово, равно как и слова, появляющиеся в процессе работы машины, ограничено с двух сторон пустыми символами #. Головка обозревает крайний слева символ заданного слова.

Работа машины состоит в повторении следующего цикла элементарных действий:

1) считывание символа, находящегося против головки;

2) поиск применимой команды, а именно той команды qa q'a'd, в которой q — текущее состояние управления, а — считанный символ;

3) выполнение найденной команды, состоящее в переводе управления в новое состояние q', записи в обозреваемую головкой клетку символа а' (вместо стираемого символа а) и последующем перемещении головки вправо, еслиd = r, влево, если d = l, или сохранении ее в том же положении, если d = р.

Машина останавливается в том и только в том случае, если на очередном шаге ни одна из команд не применима. Результат работы остановившейся машины — заключительное слово на ленте.

Машина Тьюринга, перерабатывая начальные слова на ленте в заключительные, задает словарную функцию, для которой начальные слова - значения аргумента, заключительные - значения функции. (Для представления n-местной функции начальное слово на ленте имеет вид #a₁ #a₂ # … #a_n #, где подслова a₁, a₂,…, a_n не содержат символа #. При интерпретации заключительного слова на ленте как значения функции символ # игнорируется). Если машина не останавливается, начав работу с некоторым словом на ленте, то функция, задаваемая машиной, считается неопределенной для этого слова. Таким образом, машина Тьюринга Т задает частичную функцию F_T и способ вычисления ее значений. Хотя машины Тьюринга оперируют со словами, они могут задавать и числовые функции в силу установленной выше связи между словами и числами.

По определению, функция F является (частично) вычислимой, если существует машина Тьюринга Т такая, что F_T = F. Говорят также, что для функции F существует (частичный) алгоритм вычисления ее значений, задаваемый машиной Т.

Для машины Тьюринга, как и для всех других формальных способов задания алгоритмов, включая программы для ЭВМ, характерны следующие свойства:

1) конструктивность — машина Тьюринга представляет собой конечный объект, построенный по определенным правилам из базовых объектов;

2) конечность — процесс нахождения значений функции для тех значений аргументов, для которых она определена, состоит из конечного числа шагов;

3) однозначность — результат работы машины единственным образом определяется начальным словом;

4) массовость — машина работает с любым начальным словом на ленте, составленным из символов ее алфавита.

Машина Тьюринга однозначно задается своей программой. Если упорядочить ее команды и закодировать последовательность команд словом в алфавите машины Тьюринга, то можно получить ее описание в собственном алфавите. Заметим, что одной и той же машине Тьюринга соответствуют различные словарные представления в ее алфавите в зависимости от выбора упорядочений множеств Q, V, I, но по любому из этих представлений программа машины восстанавливается однозначно.

Изучая свойства программ и их математических абстракций – схем программ, мы ставим целью автоматизацию программирования, в том числе автоматический анализ свойств программ и их преобразования, осуществляемые с помощью других, специальных программ. Поэтому нас интересуют алгоритмы, которые могли бы по любой предъявленной программе установить, завершит ли она работу или будет «циклить», дают ли две программы, исходная и оптимизированная, один и тот же результат, является ли программа синтаксически правильной и т. д.

Массовые алгоритмические проблемы формулируются следующим образом. Необходимо указать алгоритм, который бы определял, обладает ли предъявленный объект из некоторого класса объектов интересующим нас свойством, принадлежит ли он множеству М всех объектов, обладающих этим свойством. Если существует такой частичный алгоритм, то говорят, что множество перечислимо, а поставленная массовая алгоритмическая проблема частично разрешима. Если этот алгоритм к тому же всюду определен, то множество М разрешимо и поставленная проблема также разрешима. Существуют неразрешимые проблемы и даже проблемы, которые не являются частично разрешимыми, что свидетельствует о существовании невычислимых функций.

Пусть V – алфавит, М V – множество слов в V.

Характеристической функцией множества М называется предикатF_M: V^* {0, 1}, всюду определенный на V^*: F_M(а) = 1, если а М, и F_M(а) = 0, если а М.

Частичная характеристическая функция множества М – это функцияН_М: V^* {1}, определенная только для слов из М и имеющая вид Н_M(а) = 1 для всех а М.

Множество М называется разрешимым, если его характеристическая функция вычислима. Множество М перечислимо, если его частичная характеристическая функция вычислима. Разрешимость множества М означает, что существует всегда останавливающаяся (оканчивающая работу за конечное время) машина Тьюринга, позволяющая для любого слова в алфавите V через конечное число шагов установить, принадлежит ли это слово множеству М или нет. Перечислимость множества М означает, что существует машина Тьюринга, которая останавливается в том и только том случае, если предъявленное слово принадлежит множеству М.

Приведем без доказательства несколько важных теорем.

Теорема (Пост). Множество М V^* разрешимо тогда и только тогда, когда М и его дополнение М' = V^*\M перечислимы.

Машина Тьюринга, начав работу, или останавливается, или работает бесконечно. Проблема остановки формулируется так. Пусть М – множество всех пар слов в алфавите V, в каждой паре первое слово – словарное представление некоторой машины Тьюринга, второе – такое слово, что эта машина останавливается, начав работу над ним. Является ли множество М неразрешимым.

Теорема (Тьюринг). Проблема остановки машины Тьюринга неразрешима.

Последняя теорема демонстрирует существование невычислимых функций. Из тезиса Тьюринга следует, что для неразрешимых проблем нельзя построить алгоритм, который решал бы их, например, с помощью ЭВМ.

Проблема зацикливания состоит в следующем: существует ли алгоритм, хотя бы частный, который выясняет заранее для произвольной машины Тьюринга будет ли она работать бесконечно.

Теорема. Проблема зацикливания машины Тьюринга не является частично разрешимой.
Программы и схемы программ
Схемы программ - это математические модели программ, описывающие строение программы, или точнее строение множества программ, где конкретные операции и функции заменены абстрактными функциональными и предикатными символами. Следующий пример программ вычисления факториала n! и переворачивания слов поясняет различие между программами и их схемой S₁.



Функция CONSCAR приписывает первую букву первого слова ко второму слову (т. е. CONSCAR(аб, в) = ав), а функция CAR стирает первую букву слова(т. е. CAR(аб) = б).
Базис класса стандартных схем программ
Стандартные схемы программ (ССП) характеризуются базисом и структурой схемы.

Базис класса фиксирует символы, из которых строятся схемы, указывает их роль (переменные, функциональные символы и др.), задает вид выражений и операторов схем.

Полный базис В класса стандартных схем состоит из 4-х непересекающихся, счетных множеств символов и множества операторов - слов, построенных из этих символов.

Множества символов полного базиса:

1. Х = {x, х₁, х₂..., у, у₁ у₂..., z, z₁, z₂...} - множество символов, называемых переменными;

2. F = {f⁽⁰⁾, f⁽¹⁾, f⁽²⁾..., g⁽⁰⁾, g⁽¹⁾, g⁽²⁾..., h⁽⁰⁾, h⁽¹⁾, h⁽²⁾...} - множество функциональных символов; верхний символ задает местность символа; нульместные символы называют константами и обозначают начальными буквами латинского алфавита a, b, c...;

3. Р = {р⁽⁰⁾, р⁽¹⁾, р⁽²⁾...; q⁽⁰⁾, q⁽¹⁾, q⁽²⁾...; } - множество предикатных символов; р⁽⁰⁾, q⁽⁰⁾ - ; нульместные символы называют логическими константами;

4. {start, stop, ..., := и т. д.} - множество специальных символов.

Термами (функциональными выражениями) называются слова, построенные из переменных, функциональных и специальных символов по следующим правилам:

1.односимвольные слова, состоящие из переменных или констант, являются термами;

2.слово τ вида f⁽ⁿ⁾(τ₁, τ₂, ..., τ_n), где τ₁, τ₂, ..., τ_n- термы, является термом;

3.те и только те слова, о которых говорится в п.п. 1,2, являются термами.

Примеры термов: х, f⁽⁰⁾, а, f⁽¹⁾(х), g⁽²⁾(x, h⁽³⁾(y, a)).

Тестами (логическими выражениями) называются логические константы и слова вида р⁽ⁿ⁾(τ₁, τ₂,..., τ_n). Примеры: p⁽⁰⁾, p⁽⁰⁾(х), g⁽³⁾(x, y, z), p⁽²⁾(f⁽²⁾(x, y)). Допускается в функциональных и логических выражениях опускать индексы местности, если это не приводит к двусмысленности или противоречию.

Множество операторов включает пять типов:

1. начальный оператор - слово вида start(х_1, х₂...х_к), где k ≥0, а х_1, х₂...х_к - переменные, называемые результатом этого оператора;

2. заключительный оператор - слово вида stop(τ₁, τ₂,..., τ_n), где n ≥ 0, а τ₁, τ₂,..., τ_n - термы; вхождения переменных в термы τ называются аргументами этого оператора;

3. оператор присваивания - слово вида х := τ, где х – переменная (результат оператора), а τ - терм; вхождения переменных в термы называются аргументами этого оператора;

4. условный оператор (тест) - логическое выражение; вхождения переменных в логическое выражение называются аргументами этого оператора;

5. оператор петли - односимвольное слово loop.

Среди операторов присваивания выделим случаи: когда τ - переменная, то оператор называется пересылкой (х:=у) и когда τ - константа, то оператор называется засылкой (х:=а).

Подклассы используют ограниченные базисы. Так, например, подкласс V₁ имеет базис: х₁, х₂, а, f⁽¹⁾, p⁽¹⁾, start, stop, (,),:=, , и множество операторов start(х₁, х₂); х₁:=f(x₁), x₂:=f(x₂), x₁:=а, х₂:= а, р(х₁), р(х₂), stop(х₁, х₂), т. е. схемы из этого подкласса используют две переменные, константу а, один одноместный функциональный символ, один предикатный символ и операторы указанного вида.
Графовая форма стандартной схемы
Представим стандартную схему программ как размеченный граф, вершинам которого приписаны операторы из некоторого базиса В.

Стандартной схемой в базисе В называется конечный (размеченный ориентированный) граф без свободных дуг и с вершинами следующих пяти видов:

1. Начальная вершина (ровно одна) помечена начальным оператором. Из нее выходит ровно одна дуга. Нет дуг, ведущих к начальной вершине.

2. Заключительная вершина (может быть несколько). Помечена заключительным оператором. Из нее не выходит ни одной дуги.

3. Вершина-преобразователь. Помечена оператором присваивания. Из нее выходит ровно одна дуга.

4. Вершина-распознаватель. Помечена условным оператором (называемым условием данной вершины). Из нее выходит ровно две дуги, помеченные 1 (левая) и 0 (правая).

5. Вершина-петля. Помечена оператором петли. Из нее не выходит ни одной дуги.

Конечное множество переменных схемы S составляют ее память Х_S.

Из определения следует, что один и тот же оператор может помечать несколько вершин схемы.

Вершины именуются (метки вершины) целым неотрицательным числом(0, 1, 2,...). Начальная вершина всегда помечается меткой 0.

Схема S называется правильной, если на каждой дуге заданы все переменные.

Пример правильной ССП S₁ в графовой форме приведен на рисунке 1.3, а.

Вершины изображены прямоугольниками, а вершина-распознаватель - овалом. Операторы записаны внутри вершины.