ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ. Теория вычислительных процессов

• Название: Теория вычислительных процессов
• Анкор: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Дата: 01.04.2018
• Размер: 2.17 Mb.
• Имя файла: ТЕОРИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ.doc
• Тип: Документы; #17485
• страница: 5 из 20

Многоленточные автоматы



Многоленточный (детерминированный, односторонний) конечный автомат (МКА) задается так же, как ОКА. Отличие состоит в том, что множество состояний Q разбивается на n  2 подмножеств (непересекающихся) Q₁, ..., Q_n. «Физическая» интерпретация n - ленточного автомата отличается тем, что он имеет n лент и n головок, по головке на ленту. Если автомат находится в состоянии q Q_i, то i-я головка читает i-ю ленту так же, как это делает ОКА. При переходе МКА в состояние q' Q_j (ij) i-я головка останавливается, а j-я начинает читать свою ленту. МКА останавливается, когда головка на одной из лент прочитает символ .

Рассмотрим функционирование МКА с n = 2 (рисунок 1.7.) на примере сравнения пар слов в алфавите {1, 0} и допуске только совпадающих слов.

Здесь Q = Q₁ Q₂, где Q₁={q₀¹}; Q₂={q₁², q₂², q₃²}; R={q₀¹}; V={0, 1}, начальное состояние - q₀¹. МКА обрабатывает наборы слов (U₁, U₂), где слово U₁записано на первой ленте, а U₂ - на второй. Допустимое множество наборов M_A -это все возможные пары одинаковых слов, т.е. наборы, где U₁ = U₂. Например, набор может быть (1101, 1101) и т.п.

В том случае, когда слова совпадают, МКА остановится в заключительном состоянии q₀¹ (именно в этом состоянии поступит символ ) и набор будет допущен. Если слова не совпадут хотя бы в одном символе, МКА перейдет в состояние q₃², из которого не выйдет до появления символа , который и зафиксирует отсутствие совпадения слов, т.е. не допустит искаженный набор.

Доказана разрешимость проблемы эквивалентности двухленточных автоматов.

Двухголовочные автоматы
Н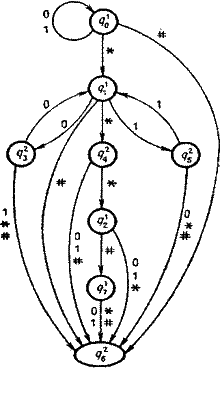есмотря на то, что двухленточные и двухголовочные автоматы похожи друг на друга, их свойства сильно отличаются. Так, проблема пустоты разрешима для многоленточных автоматов и неразрешима для многоголовочных.

Более того, в последнем случае она не является даже частично разрешимой. Проблема эквивалентности также не является частично разрешимой для многоголовочных автоматов. Однако проблема эквивалентности разрешима для двухленточных автоматов, и остается пока открытой для многоленточных автоматов с тремя и более лентами.

Двухголовочный конечный автомат (ДКА) имеет одну ленту и две головки, которые могут независимо перемещаться вдоль ленты в одном направлении. Множество состояний Q разбито на два непересекающихся множества. В состояниях Q₁ активна первая головка, а в состояниях Q₂ - вторая.

Двухголовочный автомат можно рассматривать как такой двухленточный автомат, который работает с идентичными словами на обеих лентах.

Приведем пример ДКА, который проверяет равенство двух последовательно записанных слов в алфавите V = {0, 1}. Признаком окончания каждого из слов сделаем вспомогательный символ *, не входящий в V. Автомат должен допускать только слова вида а*, а V^*. Пусть A = (V {*}, Q₁ Q₂, R, q₀¹, #, I), где Q₁ = {q₀¹, q₁¹, q₂¹, q₇¹} - множество состояний, в которых активна первая головка; Q₂= {q₃², q₄², q₅², q₆²} - множество состояний, в которых активна вторая головка; R = {q₇¹} - множество, содержащее единственное заключительное состояние. Граф автомата показан на рис. 1.8, на котором вместо многих «параллельных» дуг с разными пометками нарисована одна дуга со всеми пометками.

Находясь в состоянии g₀¹, автомат передвигает первую головку к началу второго слова и, обнаружив его, переходит в состояние q₁¹. Если конец ленты # встречается раньше символа *, автомат переходит в незаключительное состояние q₆². Если же автомат приходит к состоянию q₁¹, он считывает поочередно символы второго слова первой головкой (состояние q₁¹), а символы первого слова — второй головкой (состояния q₃² и q₅²), сравнивая эти символы. Автомат возвращается каждый раз в состояние q₁¹, если символы одинаковы. Если же обнаружится несовпадение символов или первая головка встречает конец слова раньше символа *, автомат уходит в состояние q₆². Попав в это состояние, автомат не может выйти из него; перемещая вторую головку к концу слова на ленте, он достигает #, находясь в незаключительном состоянии, так что слово на ленте отвергается. Если первая головка достигнет конца второго слова, а вторая головка обнаружит, что первое слово тоже просмотрено до конца, то автомат перейдет в заключительное состояние q₇¹. В противном случае автомат перейдет в состояние q₆², отвергая слово.

Этот пример легко обобщить на случай произвольного алфавита V, увеличивая количество состояний множества Q.

1.4.3.1. Проблемы пустоты и эквивалентности.

Будем говорить, что ДКА моделирует работу машины Тьюринга над некоторым начальным словом, если автомат допускает единственное слово — конечный протокол работы машины над ним.

Лемма (Розенберг). Существует алгоритм, который для любой машины Тьюринга и для любого начального слова строит двухголовочный автомат, моделирующий ее работу над этим словом.

Теорема. Проблема пустоты ДКА не является частично разрешимой.

Теорема. Проблема эквивалентности ДКА не является частично разрешимой.

Из неразрешимости проблемы пустоты немедленно следует неразрешимость проблемы эквивалентности, так как пустоту можно рассматривать как частный случай эквивалентности (например, эквивалентность пустому автомату, пустой машине Тьюринга и т. д.). Если же проблема пустоты разрешима (частично разрешима), то проблема эквивалентности должна исследоваться независимо, так как в общем случае из разрешимости (частичной разрешимости) пустоты не следует разрешимость (частичная разрешимость) проблемы эквивалентности. Например, проблема пустоты разрешима для многоленточных автоматов, но проблема их эквивалентности открыта (для случая трех и более лент).

1.4.3.2. Двоичный двухголовочный автомат

Cтандартные схемы могут моделировать (в уточненном ниже смысле) двухголовочные автоматы, что позволяет свести проблему пустоты этих автоматов к проблеме пустоты схем. Такое моделирование можно осуществить более простым способом, если использовать специальный класс двухголовочных автоматов, а именно класс двоичных автоматов, работающих со словами над алфавитом {0, 1}. Следующая лемма устанавливает связь между классом всех двухголовочных автоматов и специальным подклассом двоичных автоматов.

Лемма. Существует алгоритм преобразования двухголовочных автоматов в двоичные двухголовочные автоматы (ДДКА), сохраняющий пустоту автоматов(построенный двоичный автомат А_b пуст тогда и только тогда, когда пуст исходный автомат А).

Доказательство. Пусть ДКА А над алфавитом V = {a₁, a₂, ...a_n} имеет множество состоянийQ_А = {q₁^k, q₂^k, …, q_k^k}, где верхний индекс (k = 1, 2) определяет номер активной головки. Преобразование этого автомата в двоичный начнем с кодировки символов и слов из V* словами в алфавите {0, 1} по следующему правилу:

код () = 0;

код (a_i) = 11....10 (i = 1, …, n);

код (a_i) = код () код (a_i).

Так как символ  кодируется нулем, то любому непустому слову на ленте автомата А соответствует двоичное слово на ленте автомата А_b, оканчивающееся двумя нулями. Автомат останавливается, прочитав два нуля подряд (или 0, означающий пустое слово).

Автомат A преобразуется в двоичный автомат A_b так, как показано на графах рисунка 1.9. Каждый фрагмент графа А (рисунок 1.9, а) заменяется фрагментом (рисунок 1.9, б) для А_b.

После замены добавляются фрагменты (рисунок 1.9 в, г).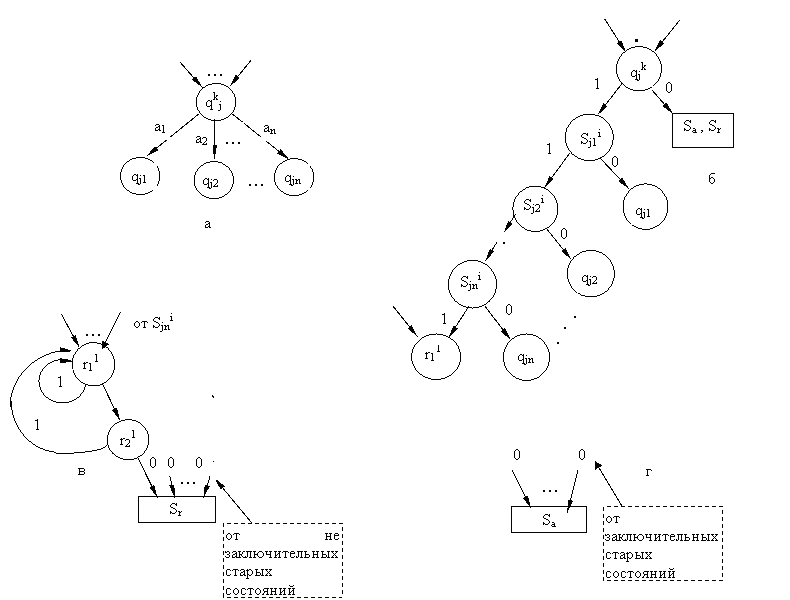

Множество состояний автомата А_bвключает:

а) все старые состояния из Q_А;

б) для каждого старого состояния q_j^kn новых состояний, n - число символов алфавита V;

в) два новых состояния r₁¹ и r₂¹.

Заключительными состояниями автомата А являются заключительные состояния автомата А_b.

Вершины S_a(останов допускающий) и S_r (останов отвергающий) носят на графе вспомогательный характер в графе А_b.Они отмечают тот факт, что автомат прочитал два нуля подряд и остановился в заключительном состоянии (случай S_a) или в незаключительном состоянии (случай S_r).

Легко убедиться, что автомат А_ьдопускает двоичное слово р тогда и только тогда, когда оно является двоичным кодом слова из V*, допускаемого автоматом А. Таким образом, из пустоты автомата А следует пустота автомата А_ь, и наоборот.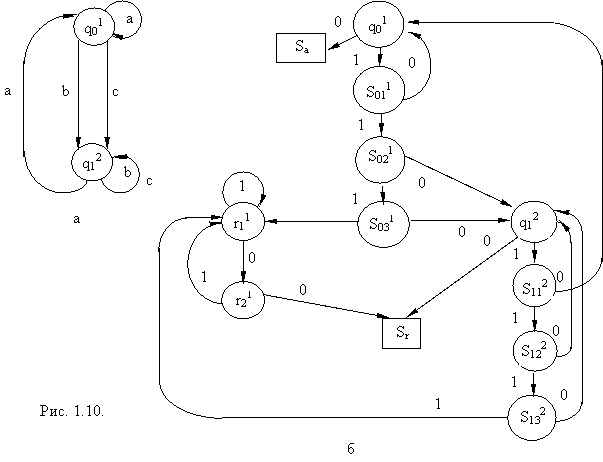


На рисунке 1.10, а приведен граф ДКА A допускающий только те слова в алфавите V = {a, b, c}, в которых символ a встречается не меньшее число раз, чем символы b и c, вместе взятые. Заключительное состояние R={q₀¹}. На рисунке 1.10, б приведен граф ДДКА, построенный по автомату А (10 – код символа a, 110 – код b, 1110 – код c).

По заданному ДДКА возможно построить ССП и наоборот, что позволяет решить задачу разрешимости (не разрешимости) свойств ССП, так как эта задача для ДДКА решена.

1.4.3.3. Построение схемы, моделирующей автомат

Двоичное слово b₁b₂ … b_nсогласовано со свободной интерпретацией базиса B, если для любого i, 1 i n, I(p) (‘f ⁱa’) = b_i, где p - единственный предикатный символ базиса B.

Пример 1.3. Слово 101010100 согласовано с любой свободной интерпретацией I такой, что для всех i 9I(p) (‘f ⁱa’) = 1 если i нечетно и меньше 9, и I(p)(‘f ⁱa’) = 0, если i четно или равно 9. Свободная интерпретация I такая, что для всех iI(p) (‘f ⁱa’) = 0, согласована с любым словом, не содержащим 1.

Для того чтобы свести проблему пустоты ДДКА к проблеме пустоты стандартных схем покажем, что для любого двоичного автомата А можно построить схему S, которая моделирует автомат А в следующем смысле. Если на ленту автомата А подано произвольное двоичное слово а, то программа(S, I), где I — любая свободная интерпретация базиса В, согласованная с а, останавливается в том и только в том случае, когда автомат допускает слово а.

Лемма. ДДКА пуст в том и только в том случае, если пуста моделирующая его стандартная схема.

Лемма. Для любого ДДКА можно построить моделирующую его стандартную схему.

Теорема (Лакхэм - Парк - Патерсон). Проблема пустоты стандартных схем не является частично разрешимой.

Теорема (Лакхэм - Парк - Патерсон, Летичевский). Проблема функциональной эквивалентности стандартных схем не является частично разрешимой.

Теорема (Лакхэм - Парк - Патерсон). Проблема тотальности стандартных схем частично разрешима.

Теорема (Патерсон). Проблема свободы стандартных схем не является частично разрешимой.
Рекурсивные схемы
Рекурсивное программирование
Среди упомянутых выше методов формализации понятия вычислимой функции метод Тьюринга — Поста основан на уточнении понятия процесса вычислений, для чего используются абстрактные «машины», описанные в точных математических терминах. Другой подход (метод Черча — Клини) основан на понятии рекурсивной функции, рекурсивная функция задается с помощью рекурсивных определений. Рекурсивное определение позволяет связать искомое значение функции для заданных аргументов с известными значениями той же функции при некоторых других аргументах. Эта связь устанавливается с помощью универсального механизма рекурсии, дающего механическую процедуру поиска значений функции. Двум подходам к определению вычислимых функций соответствуют два метода программирования этих функций — операторное и рекурсивное программирование. При операторном методе программа представляет собой явно выписанную последовательность, описаний действий гипотетической вычислительной машины (последовательность операторов, команд и т. п.).

Язык Фортран — типичный представитель операторных языков. С другой стороны, рекурсивная программа — это совокупность рекурсивных определений, задающих рекурсивную функцию, для которой аргументами служат начальные данные программы, а значением — результат выполнения программы. Известный язык рекурсивного программирования — язык Лисп — предназначен для обработки символьной информации. В других зыках комбинируют оба метода программирования. Так, Паскаль — операторный язык с возможностью рекурсивного программирования, предоставляемой механизмом рекурсивных процедур и функций.

Примером рекурсивно определяемой функции является факториальная функция FACT: Nat → Nat:

FACT(х) = 1, еслих = 0,FACT(х) =х  FACT(х - 1),если х > 0.

Операторные программы, вычисляющие значения этой функции, приведены в п. 1.1.3. Эту же функцию можно запрограммировать в некотором рекурсивном языке, базирующемся на механизме рекурсивных функций языка Паскаль:

FACT(a),

FACT(х) = ifх = 0 then1 else х  FACT(х - 1),

где а — некоторое целое неотрицательное число.

Выполнение этой программы для некоторого значения а (пусть а = 4) может быть осуществлено следующим образом. В обе части рекурсивного определения вместо х подставляется 4, после чего вычисляется правая часть определения. Вычисление правой части начинается с вычисления логического выражения. Если его значение 1 (истина), то вычисляется левое функциональное выражение (стоящее после то), а если его значение 0 (ложь) — вычисляется правое выражение (стоящее после else). Вычисление функционального выражения сводится к его упрощению, т. е. выполнению всех возможных вычислений. Если в упрощенном выражения остается вхождение символа определяемой функции FACT, то осуществляется переход к новому шагу выполнения программы. На этом шаге вхождение FACT(m), где m — значение внутри скобок после упрощения, заменяется левым (m = 0) или правым (m > 0) функциональным выражением, в котором все вхождения х заменены на m. Упрощения продолжаются до тех пор, пока не будет получено выражение, не содержащее FACT (в нашем случае это выражение — число).

Вычисление рекурсивной программы может завершиться за конечное число шагов с результатом, равным значению запрограммированной функции для заданных аргументов (начальных значений переменных), но может и продолжаться бесконечно. В последнем случае значение функции не определено.