Теплообменного

• Название: Теплообменного
• Дата: 08.03.2023
• Размер: 1.2 Mb.
• Имя файла: Teplovoy_raschet_rekuperativnogo_teploobmennogo_apparata.docx
• Тип: Учебное пособие; #974755
• страница: 13 из 22

Пример расчета секционного теплообменника типа «труба в трубе»

Задание. В секционном теплообменнике типа «труба в трубе» охлаждается воздух в количестве G₁ = 0,6 кг/с от T₁' = 70 ⁰С до T₁'' = 30 ⁰С. Воздух движется в межтрубном пространстве между большой и малыми трубками под дав- лением р₁ = 2,5 бар. Вода подается во внутренние трубки в количестве G₂ = 1,2 кг/с с температурой T₂' = 10 ⁰С. Схема движения теплоносителей – противоток. В каждой секции расположено n = 3 трубки диаметром d_вн = 32 мм, d_нар = 38 мм. Материал трубок – углеродистая сталь У8. Внутренний диаметр большой трубы D = 120 мм. Длина каждой секции l  1,8 м. Определить площадь поверхности теплообмена, а также число параллельно n₁ и последова- тельно n₂ соединенных секций.
Типрасчета– тепловой конструктивный.

При выполнении теплового конструктивного расчета определяют поверхность теплообмена, необходимую для нагрева холодного теплоносителя или охлаждения горяче- го теплоносителя до заданной температуры.

Последовательность теплового конструктивного рас- чета описана в разделе 3.2 учебного пособия.

1. 
   Из уравнения теплового баланса находим тепловую мощность аппарата Q и температуру холодного теплоноси- теля на выходе из теплообменника T₂'' (см. раздел 1.1).
   

Для однофазных теплоносителей уравнение теплового баланса примет вид:

Q = G₁с_р1 (Т₁' – Т₁'') = G₂с_р2  (Т₂'' – Т₂').

Поскольку температуры горячего теплоносителя зада- ны по условию, то из левой части уравнения теплового ба- ланса рассчитываем тепловую мощность теплообменника Q.

Для этого по табл. 1.65 [1] при средней температуре горячего теплоносителя Т₁ = (Т₁' + Т₁'') / 2 = 50 ⁰С находим

удельную теплоемкость воздуха

c_p1 ^{= 1,005 кДж/(кг·К).}

Тогда тепловая мощность аппарата равна:

Q = G₁с_р1 (Т₁' – Т₁'') = 0,6  1005  (70-30) = 24120 Вт.

Зная Q, из правой части уравнения теплового баланса находим температуру холодного теплоносителя на выходе из теплообменного аппарата:

2 2
T^"  T^' 

Q _.

G₂ c_p2

Удельная теплоемкость с_р2 зависит от искомой темпера-


2
туры T^'' , поэтому расчет ведем методом последовательных приближений.

В первом приближении примем T₂'' = T₂' = 10⁰С. По

табл. 1.74 [1] при средней температуре холодного тепло- носителя Т₂ = (Т₂' + Т₂') / 2 = 10 ⁰С находим с_р2= 4,191 кДж/(кг·К).

Рассчитываем температуру холодного теплоносителя на выходе во втором приближении:

T^"  T^'  ^Q
 10 

24120

^{ 14,80}С.

2 2 <sub>G

2</sub> c_p2 1, 2  4191

2
Расхождение между принятым и полученным значени- ями температуры T^'' составляет

  ^{10 14,8} 100%  32, 4% .

14,8

T
Погрешность итерационного процесса определения

температуры

^'' больше 5 %, поэтому расчет повторяем.

2
При этом удельную теплоемкость воды находим по табл. 1.74 [1] для нового значения Т₂'' = 14,8 ⁰С. При сред- ней температуре холодного теплоносителя Т₂ = (Т₂' + Т₂') / 2 =

= (10 + 14,8) / 2 = 12,4 ⁰С находим с_р2 = 4,189 кДж/(кг·К).

Рассчитываем температуру холодного теплоносителя на выходе в третьем приближении:

T^"  T^'  ^Q
 10 

24120
 14, 7
⁰С.

2 2 <sub>G

2</sub> c_p2 1, 2  4189

2
Расхождение между принятым и полученным значени- ями температуры T^'' составляет

  ^{14,8 14, 7} 100%  0, 68% .

14, 7

Расхождение между температурами второго и третьего приближения меньше 5 %, поэтому расчет заканчиваем. Для дальнейших расчетов принимаем температуру холод- ного теплоносителя на выходе равной Т₂'' = 14,7 ⁰С.

2. 
   Из уравнения неразрывности (1.12) определяем ско- рость движения горячего и холодного теплоносителей. При этом для секционного теплообменника типа «труба в трубе» предварительно необходимо найти количество па- раллельно n₁ соединенных секций. Алгоритм определения n₁ приведен в разделе 3.3 учебного пособия.
   

– Из уравнения неразрывности находим скорости дви- жения теплоносителей без распараллеливания потоков теплоносителей, т.е. при n₁ = 1:

1
_wn₁ 1 _ ^G_{1 ,}

 f

_wn₁ 1 _ ^G_{2 .}


2
 f

1 1 2 2

Формулы для расчета площадей поперечного сечения для прохода теплоносителей f₁ и f₂ приведены в разделе 2.2 пособия.

В данном случае воздух движется в межтрубном про- странстве, поэтому площадь поперечного сечения для про- хода горячего теплоносителя равна

^ D²

d^{2 }

_f n₁ 1 _{   n}^нар _{ n }

1 _{ 4 4 } 1

_ ^ 3,14  0,12² _{ } 3,14  0, 038^{2 } _{  }


3 2

_{ 4} 3 _{4 } 1 7, 9 10 м .

 

Вода движется в трубках, поэтому площадь попереч- ного сечения для прохода холодного теплоносителя нахо- дим по формуле (2.5)

_f n₁ 1

d²

_{ n} вн _n
2


_ 3,14 0, 032


3 1  2, 4110^3


м².

2 ₄ 1 ₄
Воздух находится под давлением, поэтому его плот- ность определяем из уравнения Менделеева-Клапейрона

р  2, 510⁵  28, 96 ₃

_{ }1 вха

  2, 696 кг/м .

¹ R T 8314  (50  273)

 1

Плотность воды находим при средней температуре Т₂ = 12,4 ⁰С по табл. 1.74 [1] ₂ = 999,34 кг/м³.

Рассчитываем скорости движения теплоносителей при n₁=1:

_{wn1 1 } G_{1 } 0, 6


 28, 2 ^м/с;

1 1
¹  f 2, 696  7,9 10^3

_wn₁ 1 _ ^G_{2 }

1, 2

 0, 498 ^м/с.

2 2
²  f 999,34  2, 4110^3

– Сравниваем значения скоростей

n₁ 1 1

w^{n1 1 с реко-}

2

1

w

и
мендуемым интервалом изменения скоростей: ^{для воздуха} 5  w^{n1 1}  25 ^;


2
^{для воды} 0,5  w^{n1 1}  3^.

Скорость холодного теплоносителя равна минимально допустимой w_min , а скорость горячего теплоносителя пре-

вышает максимально допустимую

w_max , поэтому необхо-

димо распараллеливание потока горячего теплоносителя.

– Выбираем число параллельных секций n₁ таким об-

^{разом, чтобы скорость воздуха} w₁

находилась в рекомен-

1
дуемом интервале значений. Для этого примем скорость горячего теплоносителя (воздуха), например, w^{зад = 10 м/с и определим число параллельных секций для}

движения горячего теплоносителя n₁^гор по формуле:

_wn₁ 1

28, 2

n ^гор ¹  2,82  3 .


w

1
¹ зад ₁₀


1
Уточняем f₁ и w₁ при n ^гор=3:

^ D²

d^{2 }

f  _

• 
  _n^нар _{ n}гор _
  

1 _{ 4 4 } 1


_ ^ 3,14  0,12² _{ } 3,14  0, 038^{2 } _{  2}

_{ 4} 3

3 0, 0237 м ;

4

 

1
_{w } G_{1 } 0, 6

 9,39

м/с.

₁f₁ 2, 696  0, 0237

3. 
   Строим график изменения температур теплоносите- лей вдоль поверхности нагрева Т=f(F) и рассчитываем
   

среднюю разность температур теплоносителей T . График

строим в масштабе. Правила построения графиков подроб-

но описаны в разделе 1.3 учебного пособия.

Схема движения теплоносителей – противоток. Так как Т₂ < Т₁, и соответственно W₂ > W₁ , то выпуклость кривых изменения температуры теплоносителей направле- на в сторону холодного теплоносителя – вниз.

Из графика Т=f(F) определяем максимальную и ми- нимальную разности температур теплоносителей:

Т_max= Т₁' - Т₂''= 70 – 14,7 = 55,3 ⁰С;

Т_min= Т₁'' - Т₂'= 30 – 10 = 20 ⁰С.

Т1'
					Т1'' Т2'
Т2''

Т, ⁰С 70

60

50

40

3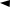0


20

10




Рис. 5.1. Изменение температур теплоносителей вдоль поверхности нагрева

Отношение

Т_max / Т_min  55,3 / 20  2,8  2 , поэтому

среднюю разность температур рассчитываем по формуле (1.21):

_{Т } ^Тmax ^{ Т}min

_ln ^Тmax

^Тmin

 ^{55, 3  20}  34, 7 ^0С.

_ln 55, 3

20

4. 
   Рассчитываем коэффициенты теплоотдачи α₁, α₂ и коэффициент теплопередачи k (см. разделы 1.4 и 1.5 учеб- ного пособия).
   

Основная сложность определения коэффициентов теп- лоотдачи α₁ и α₂ заключается в том, что в критериальные формулы входят величины, зависящие от температур наружной и внутренней стенок Т_w1 и Т_w2, поэтому расчёт ве- дут методом последовательных приближений по одному из алгоритмов, описанных в разделе 1.5. Выполним расчет по первому алгоритму.

– Задаем неизвестные температуры стенок Т_w1 и Т_w2 в первом приближении:




0

Т_w1  Т₁  Т / 2  50  34, 71/ 2  32, 65 С;

T  T 1⁰C  32, 65 1  31, 65 ^0С.

w 2 w1

• 
  По табл. 1.11 [1] при средней температуре стенки (Т_w1
  

+ Т_w2)/2 = (32,6+31,6)/2 = 32,1 ⁰С находим коэффициент теп- лопроводности углеродистой стали марки У8 λ_w = 49,54 Вт/(мК).

• 
  По критериальным уравнениям определяем коэффи- циенты теплоотдачи со стороны горячего и холодного теп- лоносителей ₁ и ₂.
  

Находим коэффициент теплоотдачи при вынужденном движении воздуха в межтрубном пространстве ₁.

При движении теплоносителя в каналах сложной фор- мы в качестве определяющего размера принимают эквива-

лентный диаметр

^R₀ ^{ d}_экв , который для межтрубного про-

странства теплообменника «труба в трубе» с числом тру- бок n рассчитывается по формуле (1.44)

^dэкв ^
2 2


D  d
нар

D  d_нар

^n 0,12²  0, 038² 3


 
n 0,12  0, 0383 ^{0, 043 м.}

По табл. 1.65 [1] при определяющей температуре Т₀ = Т₁ = 50 ⁰С находим физические свойства воздуха: λ₁ = 0,0283 Вт/(мК); Pr₁ = 0,698; µ₁ = 19,610^-6 Пас. При

температуре стенки T_w1 = 32,6 ⁰С находим Pr_w1  0, 701 .

Кинематический коэффициент вязкости для воздуха рассчитываем по формуле


ат
   /   19, 610^6 / 2, 696  7, 27 10^{6 м2/с.} Рассчитываем критерий Рейнольдса и определяем ре-

жим течения:


1
Re  ^{w1 dэкв}  ^{9,39  0, 043}  55539  10⁴ .


1
 7, 27 10^6

Число Рейнольдса больше 10000, поэтому режим тече- ния воздуха турбулентный.

По критериальной формуле (1.41) для турбулентного режима течения получим:

^ Pr

_0,25

Nu  0, 021Re^0,8 Pr^0,43_¹ _ 

1 1 1

 ^Prw1 

0,25

^ 0, 701 ^
 0, 021 55539^0,8  0, 698^0,43 ^{ 0, 698 }

 

 112, 3.

Далее рассчитываем коэффициент теплоотдачи ₁ :

1
_{ } ^Nu1 ^{ 1} _ ^{112, 3 0, 0283} _{ 73, 9}
Вт/(м^2·К).

d_экв 0, 043

Находим коэффициент теплоотдачи при вынужденном движении текучей среды в прямых гладких трубах ₂.

По табл. 1.74 [1] при определяющей температуре Т₀ = Т₂ = 12,4 ⁰С находим физические свойства воды:

λ₂ = 0,58 Вт/(мК); ₂ = 1,23410^-6 м²/с; Pr₂ = 8,92, а при тем- пературе стенки T_w2 = 31,6 ⁰С – Pr_w2  5,18 .

Определяющий размер – внутренний диаметр трубок

R₀  d_вн .

Рассчитываем критерий Рейнольдса и определяем ре- жим течения:



Re  ^{w2 dвн}  ^{0, 498 0, 032}  12914  10⁴ .


2
² 1, 234 10^6

Число Рейнольдса больше 10000, поэтому режим тече- ния воздуха турбулентный.

По критериальной формуле (1.41) для турбулентного режима течения получим:

^ Pr

_0,25

Nu  0, 021Re^0,8 Pr^0,43_² _ 

2 2 2

 ^Prw2 

0,25

^ 5,18 ^
 0, 02112914^0,8 8, 92^0,43 ^{ 8, 92 }

 

 119, 9.

Находим коэффициент теплоотдачи ₂ :




  ^Nu2 ^2  ^{119, 9  0, 58}  2172,8 Вт/(м^2·К).


2
d_вн 0, 032

• 
  Определяем коэффициент теплопередачи k. Отношение наружного диаметра стенки трубы к внут-
  

реннему диаметру меньше двух (d_нар/d_вн < 2), поэтому ко- эффициент теплопередачи рассчитываем по формуле (1.28) для плоской стенки. При этом термическим сопротивлени- ем загрязнений пренебрегаем (R_заг=0).

1
^{k } 1  1

 

₁ _w <sub>2

</sub> 1

• 
  ^Rзаг
  



 71, 2 Вт / (м²К).

1 _ 0, 003 _ 1

73, 9 49, 54 2172,8

– Уточняем температуры стенок Т_w1 и Т_w2. Для этого рас- считаем плотность теплового потока через стенку между средними температурами Т₁ и Т₂ теплоносителей


1 2
q  k(T T ) =71,2(50-12,4) = 2675,7 Вт/м².

Температуры стенок найдем по формулам (1.35) и (1.36).

T  T q /  50  2675, 7 / 73,9 13,8 ⁰С;

w1 1 1

T  T  q / 12, 4  2675, 7 / 2172,8 13, 6 ⁰С.

w 2 2 2

Расхождение между принятым и полученным значени- ями температуры составляет:

  ^{13,8  32, 65} 100%  57, 7% ,

¹ 32, 65

  ^{13, 6  31, 65} 100%  57, 0% .

² 31, 65

Так как расхождение больше 5 %, то расчет проводим аналогично пункту 4 для новых значений Т_w1 = 13,8 ⁰С и Т_w2 = 13,6 ⁰С. Заметим, что в формулах для расчета ₁ и ₂ изменятся только значение критериев Прандтля Pr_w1 и Pr_w2. Из табл. 1.11 [1] найдем коэффициент теплопроводно-

сти углеродистой стали У8 λ_w = 49,69 Вт/(мК) при средней температуре стенки

_{Т } Т_w1  Т_{w 2 } 13,8 13, 6 _{ 13, 7 0С.}