Термодинамический анализ процессов в теплоэнергетических установках

• Название: Термодинамический анализ процессов в теплоэнергетических установках
• Дата: 05.08.2020
• Размер: 1.55 Mb.
• Имя файла: ch2-gl1-6.doc
• Тип: Документы; #135221
• страница: 3 из 6

Вопросы для самоподготовки к главе 2
1. Дайте определение и расчетное выражение для эксергии вещества, находящегося в потоке.

2. Покажите графически величину эксергии в потоке для вещества, находящегося в неравновестном состоянии с окружающей средой в h,s- диаграмме.

3. Покажите графически величину потери эксергии вещества, находящегося в потоке, при адиабатном необратимом процессе его расширения в h,s- диаграмме.

4. Покажите графически величину работы возврата теплоты трениия вещества, находящегося в потоке, при адиабатном необратимом процессе его расширения в h,s- диаграмме.

5. Поясните преимущество эксергетического метода оценки необратимости адиабатных процессов расширения веществ по сравнению с использованием традиционных методов оценки необратимости в таких процессах через адиабатные коэффициенты.

3. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ ДЛЯ ПОТОКА
3.1. Основные понятия и характеристики потока
Работа многих машин и ТЭУ связана с движением рабочего тела (газа, пара и т.п.) по каналам переменного или постоянного сечения. Такая термодинамическая система будет открытой, поскольку у нее есть проницаемые для вещества границы – сечения входа и выхода рабочего тела в канале.

Движущееся по каналу рабочее тело или вещество называется потоком.

Процесс движения рабочего тела или вещества по каналу называется истечением.

Для характеристики потока, кроме термодинамических параметров (Р, v, T и т.д.), необходимо знать скорость его движения – с метр на секунду и массовый расход - G килограмм на секунду.

Допущения, принятые в технической термодинамике при изучении процессов истечения:

• 
  При изучении потоков газов и жидкостей будем рассматривать их как сплошную среду. Это правомерно, поскольку расстояние между молекулами и длина их свободного пробега несоизмеримо малы по сравнению с размерами каналов, в которых движется вещество;
  
• 
  Будем рассматривать только установившийся – стационарный режим истечения, когда все параметры и скорость газа или жидкости остаются неизменными в каждой точке пространства канала;
  

В общем случае при стационарном режиме истечения в данном сечении канала в разных его точках могут быть различные параметры и скорости. Например, при движении вещества по трубе с постоянным сечением при постоянном расходе скорость движения вещества в сечении будет у стенок трубы равна нулю из-за наличия трения, а в центре сечения она достигнет максимального значения (рис.3.1).

• 
  В дальнейшем будем рассматривать усредненные по сечению канала значения термических параметров состояния и скоростей стационарного режима истечения.
  
• 
  При стационарном режиме истечения вещества по каналу произвольного профиля с непроницаемыми стенками массовый расход вещества через любое сечение канала есть величина постоянная.
  

Доказательством этого утверждения является закон сохранения вещества – сколько вещества вошло в канал, столько же вещества и должно выйти из канала. Расход вещества в этом режиме может быть записан математически для каждого из сечений канала (рис.3.2) в виде выражения:

G = f₁c₁₁ = f₁c₁/v₁ = f₂c₂/v₂ = const ; (3.1)

Gv₁ = f₁c₁ , Gv₂ = f₂c₂ . (3.2)

где G – массовый расход вещества через любое сечение канала, кг/с;

f₁ и f₂ – площади поперечных сечений канала 1 и 2, м²;

с₁ и с₂ – скорости истечения в 1 и 2 сечениях канала, м/с;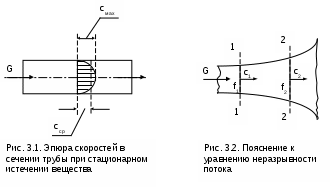


₁ – плотность вещества в сечении 1, кг/м³;

v₁ и v₂ – удельные объемы вещества в сечениях 1 и 2, м³/кг.

Уравнения 3.1 и 3.2 называются уравнениями сплошности или неразрывности потока.

3.2. Уравнение первого закона термодинамики для потока
Первый закон термодинамики для потока, так же как и для закрытой системы – для неподвижного тела, находящегося в объеме, является законом сохранения энергии для открытой термодинамической системы.

Для получения аналитического выражения первого закона термодинамики для потока рассмотрим вещество, движущееся по каналу переменного профиля (рис.3.3). Исходя из принятых ранее допущений будем считать режим движения стационарным, а параметры и скорость движения вещества одинаковыми по всей площади данного сечения канала.

В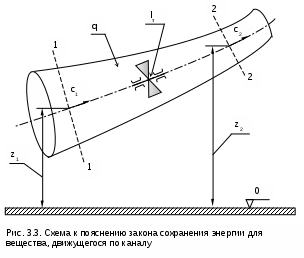
озьмем два произвольных сечения канала 1 и 2 и запишем закон сохранения энергии при перемещении вещества из сечения 1 в сечение 2.

Изменение энергии в сечении 2 по отношению к сечению 1 может произойти только за счет совершения внешних работ над потоком. В технической термодинамике в качестве таких внешних работ рассматривается теплота q и механическая работа, которая для потока получила название технической работы, обозначим ее как l_т. Присутствие технической работы можно проиллюстрировать изображением пропеллера (турбинки), установленного в потоке между сечениями 1 и 2 , вращающегося на валу. При этом вращение пропеллера возможно за счет внешней механической работы или за счет технической работы самого потока. При записи аналитического выражения первого закона термодинамики для потока воспользуемся математическим правилом сложения. Согласно этому правилу энергия потока в сечении 2 увеличится (уменьшиться), если при перемещении вещества из сечения 1 в 2 к нему будет подведена (отведена) теплота и над ним будет совершена (им будет совершена) техническая работа. Знаки перед q и l_т в этом случае принимаются исходя из того, что эти величины будут положительными, когда к потоку подводится теплота – перед q ставим знак плюс, поскольку при подводе теплоты к веществу q>0, и когда над потоком совершается техническая работа (пропеллер приводится в движение внешним источником механической работой) – перед l_т ставим знак минус, поскольку в этом случае -l_т>0 (техническая работа в цилиндре сжатия ТЭУ или в компрессоре l_т<0). Обозначив полную удельную энергию потока (для одного килограмма вещества) в сечении 1 – е₁, а в сечении 2 – е₂, запишем закон сохранения энергии для нашей термодинамической системы

е₂ - е₁ = q – l_Т . (3.3)

Полная удельная энергия потока в сечении 1 и 2 представляет сумму внутренней энергии вещества u, кинетической энергии видимого движения с²/2, потенциальной энергии относительно фиксированного нулевого уровня поверхности gz, где g – ускорение свободного падения, а z – расстояние до фиксированного нулевого уровня поверхности плюс величина работы проталкивания Рv. Работа проталкивания Рv является составляющей полной энергии потока, поскольку она совершается за счет внешнего воздействия (поршень перемещает газ в цилиндре при его поступлении через впускной клапан), т.е. для доставки килограмма вещества в данное сечение канала затрачивается внешняя работа Рv. В свою очередь, работа есть мера энергетического взаимодействия, поэтому, совершив над веществом работу проталкивания, энергия вещества увеличится на величину этой работы.

Подставив в выражение 3.3 все составляющие энергии в сечениях 1 и 2, получим выражение первого закона термодинамики для потока в интегральном виде

. (3.4)

Сумма внутренней энергии и произведения Рv есть энтальпия h. Заменив на энтальпию эту сумму в выражении 3.4, получим выражение первого закона термодинамики для потока в окончательном виде

. (3.5)

Продифференцировав уравнение 3.5, получаем выражение первого закона термодинамики для потока в дифференциальном виде

. (3.6)

Выражения 3.5 и 3.6 справедливы как для обратимых, так и для необратимых процессов. Необратимость реального процесса будет характеризоваться увеличением конечной энтальпии h₂, уменьшением конечной скорости с₂ и технической работы за счет наличия трения по сравнению с аналогичным обратимым процессом. Изменение этих величин обусловлено изменением только конечного состояния необратимого процесса и не зависит от траектории самого процес­са, т.е. внешняя теплота процесса q не изменяется, следовательно, выражение первого закона термодинамики для потока справедливо для обратимых и необратимых процессов.

В дальнейшем будут рассматриваться процессы истечения, в которых нет изменения расстояния от канала до фиксированной нулевой поверхности (dz=0). Поэтому будем рассматривать выражения первого закона термодинамики без изменения потенциальной энергии потока, т.е. принимаем gdz=0. В этом случае первый закон термодинамики для потока примет вид

; (3.7)

. (3.8)
Анализ первого закона термодинамики для потока
В выражениях 3.7 и 3.8 присутствует величина работы изменения давления в потоке h₁ - h₂+q или -dh+q. Перенеся в выражении 3.7 работу изменения давления в потоке в левую часть, запишем первый закон термодинамики для обратимого процесса истечения

. (3.9)

Из выражения 3.9 следует, что работа изменения давления в потоке в общем случае может идти на изменение кинетической энергии потока и на совершение технической работы. При этом когда нет изменения кинетической энергии (цилиндр сжатия или расширения ТЭУ), работа изменения давления в потоке равна технической работе (l_о=l_т). В случае, когда потоком не совершается техническая работа (сопловой канал, диффузор и т.п.), работа изменения давления в потоке идет только на изменение кинетической энергии потока.

Необходимо отметить, что техническая работа может быть больше работы изменения давления в потоке l_т>l_о при с₁>c₂, когда происходит уменьшение кинетической энергии (в каналах турбин). Кроме этого, возможно получение технической работы при отсутствии работы изменения давления в потоке l_о=0 за счет уменьшения кинетической энергии потока с₁>c₂, а l_т>0 (активная ступень паровой турбины, где нет изменения давления на рабочих лопатках).

Выражение действительной работы изменения давления в потоке для необратимого процесса аналогично выражению 3.9, только конечные параметры процесса, скорость в конце процесса и техническая работа будут соответствовать этому процессу (индексируются символом i):

. (3.10)

Выражение первого закона термодинамики для потока позволяет рассчитать процессы ТЭУ, в которых рабочее тело движется в каналах по замкнутому или разомкнутому контуру. В основном современные ТЭУ состоят из изобарных процессов подвода (парогенератор, поверхностные теплообменники) и отвода теплоты (конденсатор паровой турбины) и адиабатных процессов сжатия (насос, компрессор, диффузор) и расширения (турбина, сопло).

Для изобарных процессов с подводом или отводом теплоты без совершения технической работы и без изменения кинетической энергии первый закон термодинамики для потока будет иметь вид q_р=h₂ - h₁, т.е. точно такое же выражение, как и для тела, находящегося в закрытой – замкнутой системе.

Адиабатные процессы с совершением технической работы без изменения кинетической энергии описываются выражением l_o=l_т=h₁ - h₂ , эти процессы подробно рассмотрены в разделе 1.1.2. .

Неизученными остались процессы, где происходит изменение кинетической энергии потока. Остановимся подробнее на изучении этих процессов.

Вопросы для самоподготовки к главе 3
1. Что называется потоком ?

2. Что называется истечением ?

3. Какой тип термодинамической системы соответствует движению вещества по каналу постоянного или переменного сечения с непроницаемыми стенками ?

4. Какие допущения приняты в термодинамике при рассмотрении процессов истечения веществ по каналам ?

5. Поясните, какие виды энергии соответствуют веществу, движущемуся по каналу.

6. Какие виды энергетического взаимодействия вещества и внешней среды возможны при движении вещества по каналу ?

7. Напишите первый закон термодинамики для потока в интегральном виде и поясните, чем отличается его форма записи для обратимых и необратимых процессов.

8. Напишите первый закон термодинамики для потока в дифференциальном виде.

9. На что может расходоваться работа изменения давления в потоке при движении вещества по каналу ?

10. На что расходуется работа изменения давления в потоке при движении вещества в турбине ?

11. На что расходуется работа изменения давления в потоке при движении вещества в компрессоре ?

12. На что расходуется работа изменения давления в потоке при движении вещества в сопловом канале ?

13. При каких условиях возможно получить от вещества, движущегося по каналу, полезную техническую работу ?

14. Возможно ли получить полезную техническую работу от вещества, движущегося по каналу, при отсутствии работы изменения давления в потоке ?

4. ИСТЕЧЕНИЕ ГАЗА И ПАРА ЧЕРЕЗ СОПЛО
Сопловой канал – устройство для увеличения кинетической энергии потока. В сопловых каналах скорости истечения газа или жидкости велики, а длина канала мала. В таких устройствах теплообмен с окружающей средой практически отсутствует, а процесс истечения считается адиабатным (q=0). Техническая работа в сопловых каналах не производится l_т=0. Первый закон термодинамики для обратимого адиабатного процесса истечения вещества в сопловом канале будет иметь вид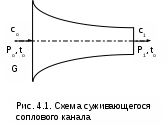

. (4.1)

В выражении 4.1 индексом о будем обозначать параметры и скорость на входе в сопло, а индексом 1 – на выходе из сопла (рис.4.1).

Для упрощения анализа процесса истечения через сопловой канал в качестве рабочего тела первоначально примем идеальный газ с постоянными теплоемкостями с_p, с_v и коэффициентом Пуассона к.

Из выражения 4.1 можно получить расчетную формулу для скорости на выходе из соплового канала:

. (4.2)

При истечении через сопло идеального газа, состояние которого изменяется по адиабате с показателем к=const, т.е. 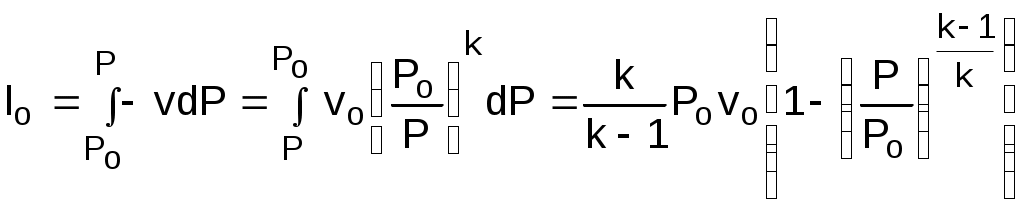, работа изменения давления в потоке при неизменных начальных параметрах газа (P_o, v_o) соответствует уравнению:

, (4.3)

а скорость истечения на выходе из сопла рассчитывается по формуле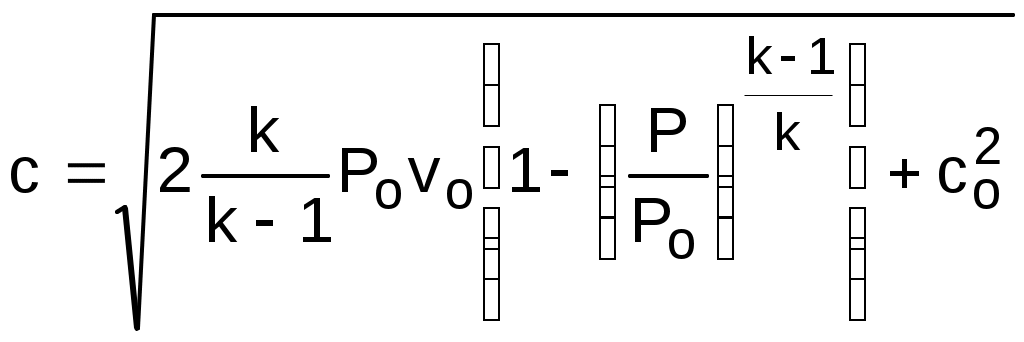

. (4.4)

Для упрощения анализа процесса истечения газа через сопло примем входную скорость, равную нулю (с_о=0). Возьмем произвольное сечение соплового канала и проведем анализ процесса истечения при изменении давления в этом сечении от Р=Р_о до Р=0, а начальные параметры будем считать постоянными. Согласно выражению (4.4) скорость истечения в этом канале будет рассчитываться по формуле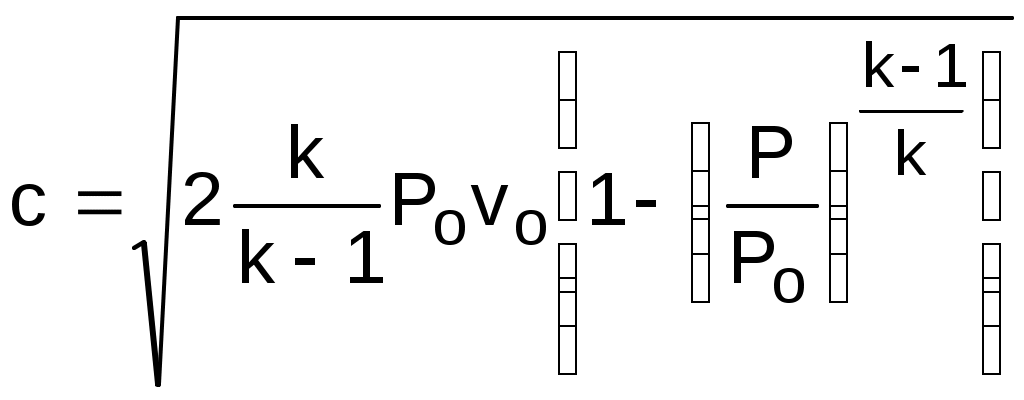

. (4.5)

Величину Р/Р_о обозначим как =Р/Р_о и назовем ее степенью изменения давления. Эта величина является определяющей в выражении 4.5, поскольку все остальные величины постоянные. Воспользуемся уравнением неразрывности потока для дальнейшего анализа в виде

. (4.6)

Величина G/f – удельный массовый секундный расход газа через единицу площади поперечного сечения сопла. Эта величина позволяет провести анализ процесса истечения газа через сопло. Выразив удельный объём газа в данном сечении соплового канала через уравнение адиабаты

(4.7)

и подставив его и выражение скорости (4.5) в уравнение (4.6), получим: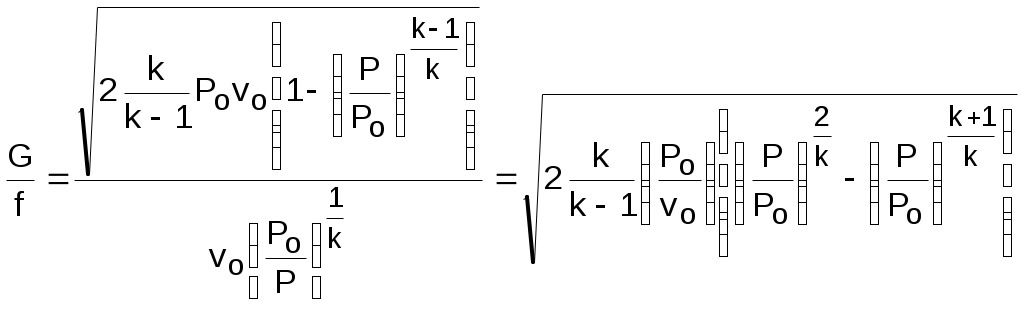

. (4.8)

Из выражения (4.8) следует, что при Р=Р_о и Р=0 удельный расход равняется нулю. В первом случае (Р=Р_о) работа изменения давления в потоке и скорость равны нулю, поэтому нет истечения и расход равен нулю; во втором случае (Р=0) удельный объём газа бесконечно велик (истечение в вакуум), а скорость истечения имеет конечное максимальное значение, соответствующее выражению:

. (4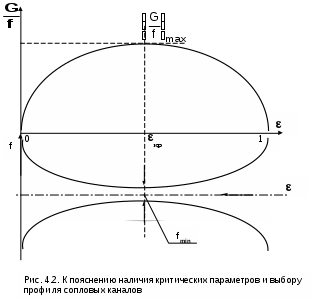.9)

У
равнение (4.8) выражает функциональную зависимость между удельным расходом газа и отношением Р/Р_о, которое обозначено через . Представим зависимость G/f = F() графически на рис.4.2. Эта функция непрерывна и положительна на интервале 0<<1, при =0 и =1 она равна нулю, следовательно, на данном интервале она имеет максимум.

Значение аргумента  при максимуме данной функции назовём критическим отношением давлений – _кр. Оно определяется как первая производная функции (4.8), приравненной к нулю. В результате такого дифференцирования получаем:

. (4.10)

Величина _кр зависит от показателя адиабаты, следовательно, для идеального газа с постоянными изобарными и изохорными теплоемкостями она постоянная (двухатомный газ к=1,4, _кр = 0,528). Для реального газа она зависит от параметров состояния (перегретый пар к1,3, _кр  0,546; для сухого насыщенного пара к  1,135, _кр  0,577).

Подставив _кр в выражение скорости истечения (4.5), получим расчетное выражение для критической скорости

. (4.11)

Итак, при истечении газа через сопло с понижением давления от Р_о до Р_кр удельный расход газа G/f сначала возрастает, при Р_кр достигает максимума, а при дальнейшем понижении давления – уменьшается. Следовательно, при постоянстве массового расхода газа G=const, по всей длине соплового канала площадь сечения в диапазоне давлений от Р_о до Р_кр должна уменьшаться, а при давлениях ниже Р_кр площадь его сечения должна увеличиваться.

Для объяснения такой закономерности изменения площади поперечного сечения канала проведём математический анализ уравнения неразрывности Gv = fc. Продифференцировав его при G = const, получим соотношение

.

Поделив последнее на Gv=fc, получим зависимость изменения относительного объема газа при истечении его в сопловом канале

. (4.12)

Из 4.12 выразим величину изменения относительной площади поперечного сечения соплового канала:

. (4.13)

Из уравнения (4.13) следует, что канал суживается (df/f < 0) в случае большего относительного возрастания скорости газа по отношению к относительному возрастанию его удельного объёма (dc/c > dv/v). В случае, когда преобладает рост относительного удельного объёма газа по сравнению с относительным ростом его скорости (dv/v > dc/c) – канал расширяется (df/f > 0). При Р_кр меняется знак df, т.е. профиль канала переходит из суживающегося в расширяющийся. В самом узком сечении канала устанавливаются параметры, называющиеся критическими (Р_кр, v_кр, t_кр, c_кр).

Для установления зависимости между критической скоростью и параметрами газа в критическом сечении сопла выразим dv/v из уравнения адиабаты Рv^k = const. Продифференцировав его и поделив на постоянную Рv^k, получим

,  ;

. (4.14)

Величину dc/c выразим из уравнения работы изменения давления в потоке для сопла:

;

, (4.15)

получим зависимость изменения площади поперечного сечения соплового канала от параметров газа и его скорости

. (4.16)

Поскольку при истечении через сопловый канал давление уменьшается (dР < 0), то канал будет суживаться (df < 0) при , и наоборот, канал расширяется (df>0) при . В самом узком сечении канала (df = 0) устанавливается критическая скорость, определяемая выражением:

. (4.17)

Из курса физики известно, что выражение (4.17) определяет скорость распространения звука в газовой среде при данных термических параметрах, обозначим её буквой а. При адиабатном истечении газа температура газа уменьшается по длине канала в направлении движения потока, следовательно, уменьшается и его скорость звука, а скорость истечения газа растёт. В суживающейся части сопла с<а._. В минимальном сечении канала скорость звука газа равна его скорости истечения: с_кр=а_кр. В расширяющейся части сопла скорость истечения газа больше скорости звука (с>а).

На рис. 4.3 представлена графическая зависимость изменения v, c, a, f при адиабатном расширении газа в сопловом канале, при G = const и изменении давления за соплом от Р=Р_о до Р=0.

При начальном давлении Р_о и удельном объёме газа v_о начальная скорость его c_о равна нулю (как приняли выше), при этом площадь сечения канала бесконечно велика (f_о=Gv_о/0=). В начале процесса расширения при Р_кр<Р<Р_о относительное возрастание скорости больше относительного возрастания объёма (функция c=F(Р) более полóгая, чем v=j(Р), а площадь сечения соплового канала уменьшается. При давлениях ниже критического Р<Р_кр, наоборот, больше относительный рост объёма по сравнению с относительным возрастанием скорости (функция v=j(Р) более полóгая, чем c=F(Р)) и площадь сечения канала увеличивается. При давлении Р=Р_кр скорость истечения равна скорости звука, здесь канал имеет минимальное сечение. Таким образом, только при наличии расширяющейся части в сопловом канале можно получить понижение давления ниже критического, а скорость истечения больше скорости звука. При Р=0 удельный объем газа стремится к бесконечности (v=), скорость истечения достигает максимального конечного значения с_мах (см. выше уравнение (4.9)), а площадь поперечного с
ечения сопла (f=Gv/c_мах) стремиться к бесконечности.

В результате проведенного анализа адиабатного процесса истечения идеального газа можно сделать выводы овыборе профиля соплового канала:

если >_кр (Р₁>Р_кр) – сопло должно быть суживающимся, истечение газа докритическое (скорость газа на выходе из сопла меньше скорости звука);

если <_кр (Р₁<Р_кр) – сопло должно быть комбинированным (сопло Лаваля) с расширяющейся частью, истечение газа сверхкритическое (скорость газа на выходе из сопла больше скорости звука).

При существующем сопловом канале, если сопло суживающееся:

при >_кр – истечение докритическое;

п
ри <_кр – истечение критическое, расширение газа в сопловом канале идёт только до критического давления (Р=Р_кр), дальнейшее расширение газа от Р_кр до давления за соплом Р₁ идёт за пределами выходного сечения соплового канала (рис.4.4 процесс 1-2).

Важно отметить, что для суживающегося или комбинированного сопла при давлении за ним ниже критического (<_кр) в самом узком сечении сопла устанавливаются критические параметры, и дальнейшее понижение давления за соплом при постоянных начальных параметрах Р_о=const и Т_о=const не влияет на массовый расход газа. При этих условиях расход газа через сопло ограничивается пропускной способностью его самого узкого сечения (рис.4.4 процессы 1-2 и 1*-2*):

. (4.18)

Увеличить расход газа через сопло можно двумя способами: – за счёт увеличения площади минимального сечения сопла, в этом случае критическая скорость и удельный объем в минимальном сечении останутся неизменными, или – за счёт повышения давления газа перед соплом, в этом случае критическая скорость идеального газа в минимальном сечении сопла может остаться прежней (_кр=Р_кр1/Р_о1=Р_кр2/Р_о2=(Т_о/Т_кр)^к/(1-к), ), а удельный объем в минимальном сечении уменьшиться (v_кр2кр1), поскольку увеличится давление в минимальном сечении сопла (Р_кр2>Р_кр1) (рис.4.4).

З
ависимость расхода газа от давления перед сопловым каналом при неизменном значении температуры на входе в сопло показана на рис. 4.5.