Термодинамический анализ процессов в теплоэнергетических установках

• Название: Термодинамический анализ процессов в теплоэнергетических установках
• Дата: 05.08.2020
• Размер: 1.55 Mb.
• Имя файла: ch2-gl1-6.doc
• Тип: Документы; #135221
• страница: 5 из 6

max.

Точками 1, 2, 3, 4, 5 обозначены возможные начальные и конечные состояния пара при дросселировании. Последовательно дросселируя перегретый пар от состояния точки 1 с давлением Р₁ до состояния точек 2, 3, 4, 5, получаем сухой насыщенный пар с Р₂ (точка 2), влажный насыщенный с Р₃ (точка 3), снова сухой насыщенный пар с Р₄ (точка 4) и снова перегретый пар с Р₅ (точка 5). Все эти процессы дросселирования сопровождаются снижением температуры пара. В случае если h₁>h"_max при тех же давлениях Р₁ – Р₅ процесс дросселирования будет идти только в области перегретого пара. При дросселировании реальных веществ может наблюдаться не только понижение температуры, но и повышение, и постоянство её.

Впервые изменение температуры реальных газов в результате дросселирования было экспериментально установлено Джоулем и Томсоном в 1852 году, поэтому это явление называется эффектом Джоуля – Томсона.

Изменение температуры реальных веществ в результате адиабатного дросселирования объясняется энергетическим взаимодействием молекул. Из равенства энтальпий в начале и конце процесса дросселирования следует:

u₂+Р₂v₂=u₁+Р₁v₁ или u₂-u₁=Р₁v₁-Р₂v₂ .

В свою очередь, изменение внутренней энергии реального газа можно представить как сумму изменений кинетической – u_к и потенциальной – u_п составляющих внутренней энергии

u₂-u₁=u_к+u_п . (5.3)

Изменение потенциальной составляющей внутренней энергии в процессе дросселирования реальных газов и пароввсегда положительно, т.к. при снижении давления в этом процессе происходит увеличение объема, что приводит к увеличению расстояния между молекулами, а следовательно, и к увеличению потенциальной составляющей внутренней энергии гравитационного их взаимодействия u_п>0 (для идеальных газов u_п=0).

Изменение кинетической составляющей внутренней энергии определяет знак изменения температуры, поэтому запишем выражение (5.3) в виде

u_к=-(u_п+Р₂v₂-Р₁v₁) . (5.4)

Из выражения (5.4) видно, что изменение кинетической составляющей внутренней энергии определяется соотношением двух слагаемых: u_п и (Р₂v₂ - Р₁v₁). Первое слагаемое всегда положительно, а второе может быть положительным, отрицательным и нулем. Выражение второго слагаемого детально анализировалось в разделе "реальные газы" [2]. Для реальных газов и паров величина (Р₂v₂-Р₁v₁) или (d(Рv)/dР)_h характеризует их сжимаемость -(dv/dР)_h по отношению к сжимаемости этих же идеальных газов.

В случае, когда (Р₂v₂-Р₁v₁)=0, сжимаемость реальных и идеальных газов одинакова, свойства реальных газов близки к идеальным, т.е. u_п=0 и получается, что нет изменения кинетической составляющей внутренней энергии при дросселировании (u_к=0), а следовательно, не изменяется и их температура в этом процессе.

При (Р₂v₂-Р₁v₁)>0 – сжимаемость реальных газов меньше, чем идеальных, u_п>0, следовательно u_к<0, и температура в процессе дросселирования уменьшается.

В случае, когда (Р₂v₂-Р₁v₁)<0, сжимаемость реальных газов больше, чем идеальных, u_п>0, следовательно возможна ситуация, когда (u_п+(Р₂v₂-Р₁v₁))<0, а u_к>0, и температура в процессе дросселирования будет увеличиваться. Разумеется, в этом случае также возможно и уменьшение температуры и ее неизменность в результате процесса дросселирования.

Для идеального – условно изоэнтальпийного процесса дросселирования можно представить зависимость изменения температуры от изменения давления в дифференциальном виде

dT_h = _hdР . (5.5)

Коэффициент пропорциональности _h называется коэффициентом адиабатного дросселирования, дифференциальным дроссель-эффектом или дифференциальным эффектом Джоуля–Томсона. Знак коэффициента адиабатного дросселирования _h определяет знак изменения температуры: при _h>0 dT_h<0, а при _h<0 dT_h>0.

Изменение температуры вещества в результате его адиабатного дросселирования при конкретном изменении давления называется интегральным дроссель–эффектом.

Рассмотрим интегральный дроссель–эффект для воды и водяного пара в h,s- диаграмме. Ранее (рис. 5.5) был рассмотрен случай понижения температуры. На рис. 5.6 представлен случай адиабатного дросселирования жидкой фазы воды при высоком давлении и низкой температуре. В точке А температура воды t_о=0 ^oC. В процессе дросселирования от точки А до точки 3, лежащей на x=0, температура жидкости повышается. В области влажного насыщенного пара (точка 4) температура понижается. На линии х=0 меняется знак дифференциального дроссель–эффекта. В точке 4 температура такая же, как в точке 2.

На рис. 5.7 представлены процессы адиабатного дросселирования жидкости в области высоких температур. В этой области есть изотермический минимум для процессов дросселирования. В процессе дросселирования 1-2 температура повышается, на 2-3 понижается. В точке 2 изменение температуры при дросселировании меняет знак с положительного на отрицательный.

Точки, в которых меняется знак дифференциального дроссель-эффекта, называются точками инверсии, а линия, образуемая ими – линией инверсии.

Н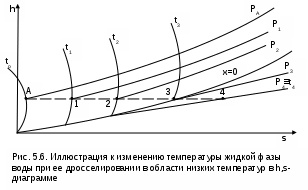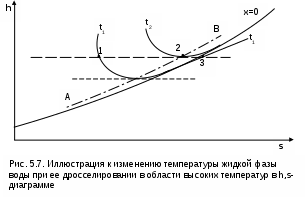

а рис.5.6 линия инверсии совпадает с нижней пограничной кривой х=0. На рис.5.7 линия инверсии АВ проходит через изотермические минимумы жидкой фазы воды.

Линии инверсии, как любая совокупность точек, определяющих состояние вещества, могут быть изображены в системе координат с любыми независимыми параметрами состояния.

На рис.5.8 показан вид линий инверсии для воды и водяного пара в системе координат Р,Т.

З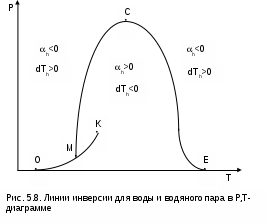
десь линияОК соответствует линии фазового перехода воды (в точке К Т=T_кр). На участке ОМ она совпадает с линией инверсии (в точке М t=235 ^оС). Левая – ОМС и правая – СЕ ветви инверсии имеют максимум в точке С, в которой Р_с10Р_кр и Т_с3Т_кр. В точке Е Т_Е7Т_кр. В области, заключенной между линией инверсии и осью температур ОМСЕО _h>0 т.е. при адиабатном дросселировании здесь температура уменьшается. На всей остальной площади диаграммы _h<0, и при адиабатном дросселировании воды температура ее увеличивается.

Вопросы для самоподготовки к главе 5
1. Дайте определение процессу дросселирования.

2. Напишите уравнение адиабатного процесса дросселирования и охарактеризуйте поведение энтальпии, скорости и давления в этом процессе.

3. Объясните, чем вызвано снижение давления в процессе дросселирования.

4. Покажите в h,s- диаграмме как изменяется работа изменения давления и эксергия вещества в процессе его дросселирования.

5. Объясните изменение температуры в процессе дросселирования реальных газов и паров – эффект Джоуля-Томсона.

6. Покажите в в h,s- диаграмме как изменяется температура водяного пара в процессах его дросселирования.

7. Покажите в h,s- диаграмме как изменяется температура воды в процессах ее дросселирования.

8. Что значит область инверсии (линия инверсии) в процессе дросселирования реальных веществ ?

6. СМЕШЕНИЕ ГАЗОВ И ПАРОВ
Во многих технических устройствах происходят процессы смешения различных веществ с различными параметрами. Смесь из нескольких веществ, находящихся в газообразном состоянии, может быть получена при осуществлении процесса смешения по одному из следующих способов:

– смешение в объёме;

– смешение в потоке;

– смешение при заполнении объёма.

Для капельных несжимаемых жидкостей возможны только два первых способа смешения.

Ограничимся рассмотрением адиабатных процессов смешения при отсутствии химических реакций между веществами и без совершения ими технической работы.

При рассмотрении процессов смешения веществ задача сводится к определению параметров состояния получающейся смеси и оценке необратимости этих процессов посредством оценки увеличения энтропии системы и потери возможной работы – эксергии.

6.1. Смешение в объёме
Смешение в объёме – это смешение веществ (газов, паров, жидкостей) за счёт их взаимного диффузионного проникновения после удаления (разрушения) разделяющих их непроницаемых перегородок и без изменения суммарного объёма веществ.

Допустим, что в двух отсеках сосуда (рис. 6.1) объёмом V, разделённого адиабатной перегородкой, находятся разные газы при разных давлениях и температурах. Перегородка разрушается и происходит диффузионное смешение газов. При этом масса смеси оказывается равной сумме масс смешивающихся газов:

m_см = m₁ + m₂ ,

а объём – сумме первоначальных объёмов этих газов:

V_см = V₁ + V₂ .

В результате удельный объём смеси двух или более компонентов газов будет определятся как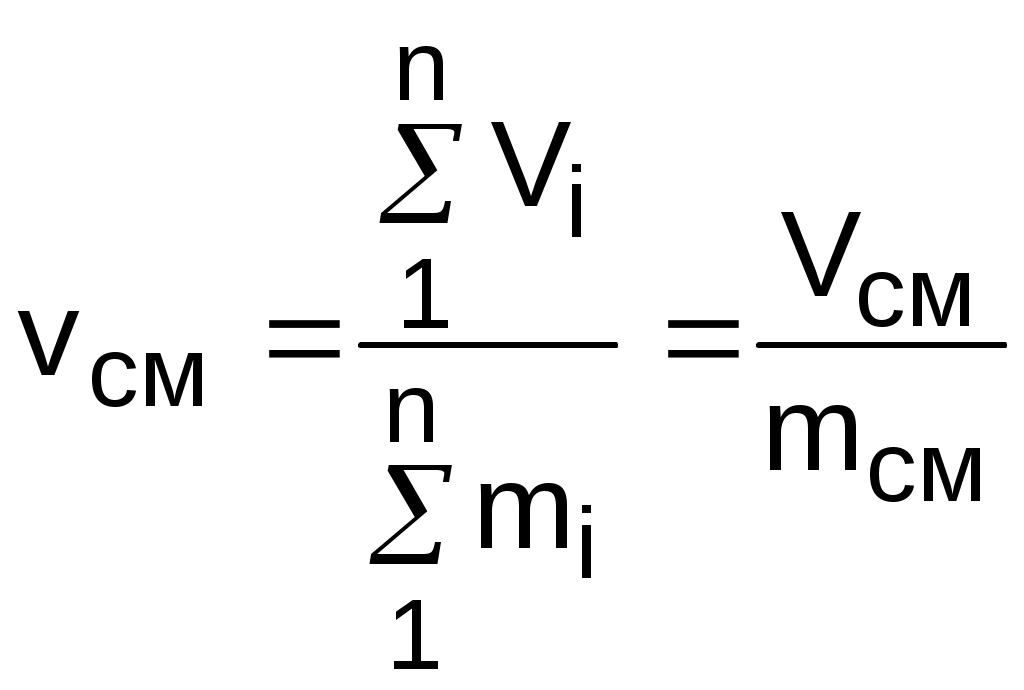

. (6.1)

где n – число смешивающихся компонентов газа.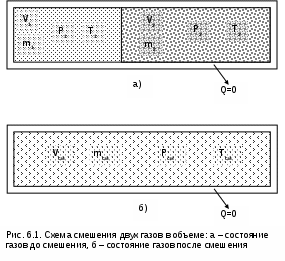


Для определения параметров состояния смеси газов, с известным массовым составом и известными параметрами газов до смешения, необходимо знать ещё один параметр. Он определяется на основании первого закона термодинамики для данной системы

.

При адиабатном смешении газов без изменения общего объёма сосуда, теплота и работа изменения объема равны нулю (Q=0, L=0). Следовательно, изменения внутренней энергии в системе нет, т.е. внутренняя энергия после смешения равна сумме внутренних энергий компонентов смеси до смешения:

. (6.2)

Используя аддитивные свойства (подчинение закону суммирования) внутренней энергии, после деления выражения (6.2) на массу смеси, получаем расчётное выражение удельной внутренней энергии газа после смешения:

, (6.3)

где g_i – массовые доли компонентов смеси газов.

Удельный объём (v_см) и удельная внутренняя энергия (u_см) при известном составе смеси определяют состояние смеси. По ним могут быть найдены остальные параметры смеси. Для реальных газов они обычно определяются по таблицам термодинамических свойств веществ.

Для идеальных газов внутренняя энергия – функция только температуры, и поэтому задача определения параметров смеси упрощается. Приняв начало отсчёта внутренней энергии при 0 ^oC и считая постоянной изохорную теплоемкость идеальных газов, можно записать:

u - u_о = c_v(t - 0) или u = c_vt + u_о . (6.4)

Используя выражение (6.4) для определения всех внутренних энергий газов, получим выражение (6.3) для смеси идеальных газов в виде

, (6.5)

где c_vi – массовые изохорные теплоёмкости компонентов смеси газов;

t_i - температура компонентов смеси газов до начала процесса смешения, ^oC;

u_оi – удельная внутренняя энергия компонентов смеси газов до начала процесса смешения при 0 ^oC.

По закону сложения (аддитивности) внутренняя энергия смеси газов при 0 ^oC будет равна сумме внутренних энергий ее компонентов при той же температуре:

. (6.6)

Следовательно, выражение (6.5) примет вид

. (6.7)

Выразив теплоёмкость смеси газов через сумму теплоемкостей ее компонентов

,

получим из уравнения (6.7) расчётное выражение для температуры смеси идеальных газов: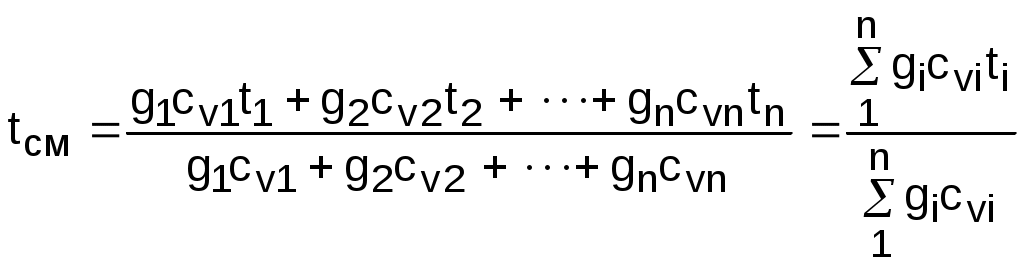

. (6.8)

Выражение (6.8) справедливо и при подстановке всех температур по абсолютной шкале Кельвина.

Далее, зная v_см и T_см для идеальных газов, можно определить давление смеси, используя уравнение состояния идеального газа:

,

где .

Изменение энтропии системы в расчёте на один килограмм смеси определяется как сумма изменений энтропий компонентов смеси газа:

, (6.9)

где Δs_i = s_iсм - s_i – изменение энтропии одного компонента смеси газа от начальных параметров до параметров смеси. Выражение (6.9) справедливо для реальных и идеальных газов.

Для идеальных газов Δs_i рассчитывается по формулам идеальных газов, через любую пару параметров. При этом необходимо использовать параметры парциального давления каждого компонента смеси газа. Например, для первого компонента можно записать:

, (6.10)

где – парциальное давление первого компонента смеси газа при температуре смеси, когда этот газ занимает весь объем.

Потери потенциальновозможной полезной работы газа (эксергии) в этом необратимом процессе ведутся традиционно по теореме Гюи-Стодолы [1]:

.

Используя выражения 6.1  6.8, можно решить и обратную задачу – нахождения масс или массовых долей компонентов смеси данных газов при известных их начальных параметрах, необходимых для получения необходимых параметров смеси газов.

6.2. Смешение в потоке
Смешение в потоке – это слияние нескольких потоков веществ в общий поток.

Давление вещества в месте смешения должно быть ниже минимального или равно минимальному давлению смешивающихся потоков, т.е. в расчетах оно должно быть задано. Рассмотрим пример адиабатного смешения потоков в трубопроводах (рис. 6.2). О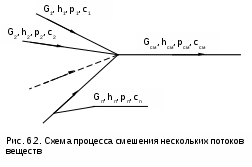
бозначим расходы смешивающихся потоков как G₁, G₂,..., G_n.

Предположим, что известны массовые расходы потоков, параметры смешивающихся потоков и давление смеси. Воспользуемся для этого процесса смешения уравнением первого закона термодинамики для потока при отсутствии теплообмена системы с внешней средой (q=0) и отсутствии технической работы (l_т=0):

. (6.11)

В технических устройствах кинетическая энергия потоков, а соответственно и её изменение в процессе смешения, очень малы по отношению к энтальпиям смешивающихся веществ, поэтому обычно условно принимают, что c₁=c₂=···=c_n=c_см, а так как G_см=G₁+G₂+...+G_n, то уравнение первого закона термодинамики для потока будет иметь вид

(6.12)

или, используя массовые доли компонентов смеси , получим выражение 6.12 в виде

. (6.13)

Давление Р_см и энтальпия h_см определяют состояние смеси вещества заданного состава. Определение других параметров смеси реальных веществ ведётся по таблицам термодинамических свойств отдельных компонентов. Проще выполняется определение параметров смеси потоков веществ с одинаковыми физическими свойствами (например, воды и водяного пара). В этом случае используются таблицы термодинамических свойств данного вещества.

Ещё проще по Р_см и h_см определяются все остальные параметры смеси идеальных газов. Для идеальных газов, приняв начало отсчета энтальпии от 0 ^оС и используя ее постоянные изобарные теплоемкости, уравнение (6.13) можно представить в виде

. (6.14)

Все преобразования энтальпий идеальных газов в уравнении (6.14) аналогичны преобразованиям внутренних энергий для случая смешения в объёме. Температура смеси, выраженная из (6.14), определяется как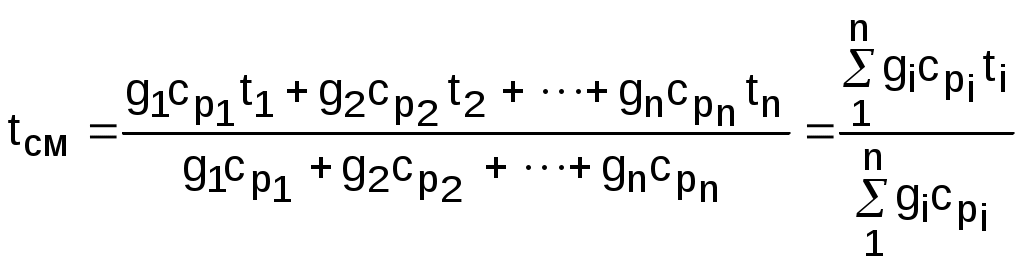

. (6.15)

Выражение (6.15) справедливо и при подстановке в него всех температур по абсолютной шкале Кельвина.

По Р_см и t_см для идеальных газов могут быть определены все другие параметры смеси, например:

,

где – .

Необратимость процесса смешения в потоке оценивается по увеличению энтропии системы аналогично смешению в объёме по формуле (6.9). Для идеального газа изменение энтропии каждого потока смешения определяется по температуре и давлению до смешения, и по температуре смеси и парциальному давлению этого компонента смеси (6.10). Например, для первого потока

,

где – , а объемная доля данного компонента смеси газа может быть определена через массовую долю как

.

Потеря эксергии при смешении в потоке определяется, как во всех случаях, по формуле Гюи-Стодолы [1].

Изменение параметров при смешении в потоке и необратимость этого процесса можно наглядно показать в h,s- диаграмме. Наиболее просто это можно сделать для процессов смешения потоков одного и того же вещества с разными начальными состояниями. Такие процессы широко используются в технике, например: смешиваются в общем паропроводе два потока пара; вспрыски воды в паропроводы для регулирования перегрева пара; смешение в эжекторах, струйных насосах и т.д..

Рассмотрим смешение двух потоков одного и того же газа с различными начальными параметрами, определяемыми точками 1 и 2 в диаграмме h,s (рис. 6.3).

В соответствии с формулой (6.13) для двухкомпонентной смеси ее энтальпия определяется как

, (6.16)

учитывая, что g₁+g₂=1 или g₁=1-g₂, получаем из (6.16) соотношения для массовых долей смеси:

,

или отношение массовых расходов:

. (6.17)

Таким образом, графическое определение энтальпии смеси сводится к делению отрезка прямой 2'-1' – точка М' или 1-2 – точка М_о пропорционально массовым долям смешивающихся потоков. Аналогично энтальпии смеси в точке M_о энтропия этой точки соответствует значению

s* = g₁s₁ + g₂s₂ . (6.18)

Действительная энтропия смешивающихся потоков находится правее точки M_о на линии постоянной энтальпии h_см и соответствует точке M, т.к. процесс смешения необратим и характеризуется увеличением энтропии системы на величину

. (6.19)

Прямая 1-2 называется прямой обратимого смешения. Она позволяет графически показать увеличение энтропии системы в процессах смешения потоков.

Приведём некоторые типичные процессы смешения потоков и их графическое представление в h,s- диаграммах.

На рис. 6.3 показан процесс смешения двух потоков одного газа с одинаковыми давлениями и разными температурами. До смешения состояние газов соответствовало точкам 1 и 2 , после смешения – точке M. Все точки лежат на одной изобаре. Проведя прямую 1-2, на пересечении её с h_см найдём точку M_о. Разница энтропий точек M и M_о соответствует увеличению энтропии системы в данном процессе смешения потоков газа.

Н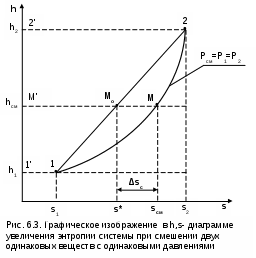
а рис. 6.4 представлен процесс смешения двух потоков одного газа при разных давлениях и температурах. При этом давление смеси равно меньшему давлению одного из потоков, т.е. Р₂>Р₁=Р_см. Возрастание энтропии за счёт необратимости процесса смешения в этом случае вызывается не только необратимостью теплообмена между потоками, но и дросселированием второго потока до давления первого.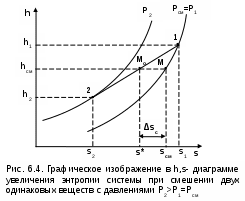




Н 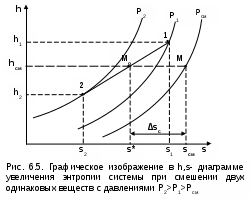а рис. 6.5 представлен процесс смешения двух потоков одного газа при разных давлениях и температурах. При этом давление смеси меньше давления меньшего из смешивающихся потоков, т.е. Р₂>Р₁>Р_см.

На практике возможно частичное использование располагаемой работы потока высокого давления для повышения давления потока с низким давлением в специальных устройствах смешения – эжекторах. На рис. 6.6 и приведена схема такой установки, а на рис. 6.7 изображён идеальный процесс смешения потоков одинаковых веществ в эжекторе.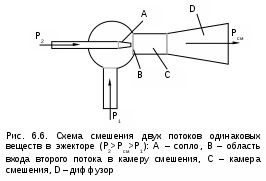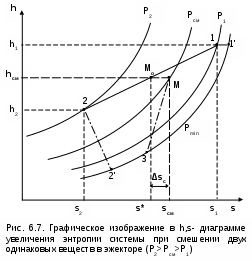




Для пояснения этого процесса его можно условно разбить на три составляющие: адиабатное необратимое дросселирование первого потока через кольцевой зазор В до давления в камере смешения (процесс 1-1’) и процесс необратимого адиабатного истечения газа через сопло А второго потока (процесс 2-2’), оба эти процесса идут до давления P_min в камере смешения С, которое ниже давления смеси и давления Р₁. Далее идёт процесс смешения этих потоков при постоянном давлении P_min до состояния, соответствующего точке 3, после чего в диффузорной части эжектора D идёт процесс необратимого адиабатного торможения потока до давления Р_см (процесс 3M).

Увеличение энтропии системы в этом случае определяется также с помощью прямой 1-2 в виде отрезка прямой М_оМ.

Основные потери эжектора обусловлены необратимостью перемешивания в камере смешения двух потоков с разными параметрами и разными скоростями.