Логика. 0011230_ЛОГИКА. Тестирующая система

• Название: Тестирующая система
• Анкор: Логика
• Дата: 07.02.2023
• Размер: 410 Kb.
• Имя файла: 0011230_ЛОГИКА.doc
• Тип: Документы; #923688
• страница: 4 из 10

Род и вид

 

Понятие с большим объемом по отношению к понятию с меньшим объемом называется родовым понятием, или, просто, родом. Понятие с меньшим объемом по отношению к понятию с большим объемом называется видовым понятием, или, просто, видом. Отношение рода и вида называется родо-видовым отношением.

 

Это отношение не надо путать с отношением вида и индивида. Например, отношение таких понятий, как «человек» и «Иванов», будет отношением вида и индивида, а не рода и вида. В некоторых случаях это имеет значение.

 

«Древо Порфирия»

 

Греческий философ-неоплатоник Порфирий (233-304) попытался в свое время построить схему, получившую название «древо Порфирия», которая охватывала бы собой все родовидовые отношения, начиная от отдельного индивида и кончая высшим родом, которым является бытие. Понятие бытия означает все, что существует. В понятие бытия входят понятия «телесное бытие» и «бестелесное бытие». «Тело» содержит в своем объеме одушевленные тела и неодушевленные. Одушевленные тела или организмы делятся на «чувствующие организмы» и «нечувствующие организмы» (растения). «Чувствующие организмы» содержат в своем объеме «разумные существа» и «неразумные существа» и т.д. Это «древо» выглядит следующим образом:

 



Если изобразить это на кругах Эйлера, то все это «древо» будет выглядеть так: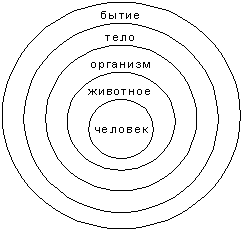

 



 

Ближайший род

 

Из приведенной картинки видно, что человеку «ближе» животное, чем бытие, и организм «ближе», чем тело. Но есть такой род для каждого вида, «ближе» которого нет. Он-то и называется ближайшим родом. Таким родом для «человека» является «животное». Ближайшему роду можно дать следующее определение: ближайшим родом по отношению к данному виду является тот и тогда, когда нет третьего понятия, которое было бы родовым по отношению к данному виду и видовым по отношению к данному роду.

 

На кругах это можно выразить так: А является ближайшим родом по отношению к В,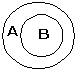

 



 

если нет такого С, когда имело бы место следующее:

 



 

Если такое есть, то уже не А, а С будет ближайшим родом по отношению к В.

 

Ограничение и обобщение

 

Переход от понятия с меньшим объемом к понятию с большим объемом называется обобщением понятия. Переход от понятия с большим объемом к понятию с меньшим объемом называется ограничением понятия. Эти процессы можно изобразить при помощи следующей схемы: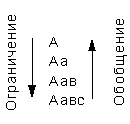

 



 

Допустим, у нас есть понятие А — человек. Из него при помощи видового отличия а - русский, можно образовать вид, русский человек. Если, далее, прибавить к понятию Аа видовое отличие в — проживающий в г. Москве, получим: русский человек, проживающий в Москве. Если сюда добавить еще видовое отличие с — токарь по профессии, то получим: русский человек, проживающий в Москве, токарь по профессии.

 

Это было ограничение понятия «человек». Можно идти наоборот, по пути элиминации видовых признаков, и тогда мы будем иметь дело с обобщением понятия.

 

Категории

 

Категориями называются наиболее общие понятия, или высшие роды. Таким родом является, например, бытие. По отношению к бытию уже нет более общего понятия. Оно есть высший род. Категориями также являются: субстанция, количество, качество, отношение, место, время, положение, обладание, действие, страдание. Эти категории и выделил в свое время Аристотель. Поскольку категории, по определению, являются высшими родами бытия, то они сами не могут быть видами, кроме как по отношению к понятию «категории»: все они виды категорий. Но между самими категориями нельзя установить родо-видовое отношение. Особые отношения между категориями определяются и изучаются в метафизике или в диалектике. Логика эти отношения не изучает.

 

Отношения между понятиями

 

Имеются в виду отношения между понятиями по объему. Мы уже имели дело с родо-видовым отношением понятий. Это и есть один из видов отношений между понятиями по объему. Это отношение называется также отношением подчинения:

 



 

Понятие А подчиняет себе понятие В, а понятие В является подчиненным понятию А.

 

Понятия сравнимые и несравнимые. Возьмем два понятия, «душа» и «треугольник». Для этих двух понятий нет ближайшего общего рода, видами которого они являлись бы. И потому их невозможно сравнивать. Необходимо подчеркнуть, что речь идет именно о ближайшем общем роде, потому что просто общий род можно найти даже для очень непохожих вещей. Например, и телеграфный столб, и американский миллионер имеют в качестве общего рода «предмет», то есть понятие предмета.

 

Для сравнимых понятий существуют следующие отношения:

 

1. Тождества. Это отношение между понятиями, объемы которых совпадают, только они по-разному выражены. Например, понятия «холостяк» и «неженатый человек». Это отношение на кругах Эйлера выглядит так

 



 

где А — холостяк, а В — неженатый человек.

 

2. Пересечения. Отношением пересечения называется отношение между понятиями, объемы которых частично совпадают. Например, объемы понятий «студент» и «спортсмен» частично совпадают, потому что есть студенты, которые являются спортсменами, и есть спортсмены, которые являются студентами. Но не все спортсмены — студенты и не все студенты — спортсмены.

 



 

3. Подчинения. В отношении подчинения находятся понятия, объем одного из которых полностью входит в объем другого, а объем последнего шире, чем объем первого.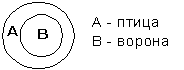

 



 

4. Соподчинения. В отношении соподчинения находятся такие понятия, для которых существует общее родовое понятие, в объем которого они оба входят.

 



 

5. Противоречия. В отношении противоречия находятся понятия, которые отрицают друг друга и исключают друг друга и в объем другого входит все, что не входит в объем первого.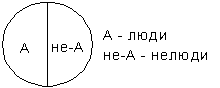

 



 

Объем понятия не-люди являетсяв данном случае универсальным, потому что в него входит все, что не есть человек, — дерево, телеграфный столб, Луна, Солнце и т.д.

 

6. Противоположность. Аристотель определял противоположность как максимум различия. В общем это верно, но требует разъяснения. Если мы, допустим, будем брать разные оттенки черного цвета, то каждый из них более или менее черный. И если какой-то из них менее черный, то он более белый. Поэтому на разных концах всего спектра черно-белых цветов будут находиться два цвета — черный и белый, которые и называются противоположными, или противными. Схематически это можно изобразить так:

 



 

Другие примеры: «добрый» и «злой», «высокий» и «низкий», «красивый» и «безобразный», «громкий» и «тихий», «глубокий» и «мелкий», «левый» и «правый» и т.д.

 

Вместе с тем ясно, что черный — это не белый. Но не-белый, не значит — черный. Поэтому противоположность оказывается частным случаем противоречия:

 



Определение понятия

 

Любая наука, — в том числе и логика, как мы видели, — начинается с определений. Противоположность есть то-то и то-то. Противоречие есть то-то и то-то. И если этих определений не давать, то очень легко спутать то и другое. Если нет определений, то это не наука, а если человек не знает определений, то он и не знает науки. Поэтому от студента на зачете или экзамене требуют: дайте определение закона, дайте определение гражданского права, дайте определение денег и т.д. Определением в логике называется логическая операция, устанавливающая объем и содержание понятия, или значение того или иного слова или термина.

 

Логика изучает только форму определения. По форме всякое определение состоит из определяемого и определяющего. Когда мы говорим: противоположность есть максимум различия, то «противоположность» здесь определяемое, а «максимум различия» — определяющее. Само определяющее, в свою очередь, делится на ближайший род, genus proximum, и видовое отличие, differentia specifica.

 

Что такое «род» и «вид», мы уже знаем. Определение и есть установление вида внутри его рода. Родом для противоположности является различие, а противоположность — вид различия.

 

Существуют правила определения. Таких правил четыре.

 

1. Определение должно быть соразмерным. Это означает, что объем определяемого должен быть равен объему определяющего. Нарушением этого правила является часто отсутствие указания на видовое отличие. Например, «треугольник есть плоская геометрическая фигура». Здесь указывается ближайший род и не указывается видовое отличие. Такое определение является слишком широким, потому что в объем понятия «плоская геометрическая фигура» войдут и квадрат, и параллелограмм, и круг, и другие плоские геометрические фигуры, а не только треугольник.

 

И наоборот, определение может быть слишком узким. Если мы, например, определим треугольник как «плоскую геометрическую фигуру, имеющую три равные стороны», то мы, тем самым, определим равносторонний треугольник, и сюда не войдут все другие виды треугольников.

 

2. Определение не должно содержать круга. Кругом называется такая ошибка в определении, когда определяющее само может быть определено только через определяемое. Если взять, например, определение «вращение есть движение вокруг оси», то здесь само понятие «ось» может быть определено только через «вращение».

 

Определение, содержащее круг, называется тавтологией. Тавтология — это повторение того же самого, только другими словами. А в определении определяемое и определяющее должны быть двумя разными понятиями.

 

3. Определение не должно быть отрицательным. Отрицательным называется такое определение, когда в определяющей части указываются те признаки, которые не принадлежат определяемому. Например, «треугольник есть плоская геометрическая фигура, не имеющая четырех сторон». Недостатки такого определения понятны, потому что оно почти всегда является слишком широким.

 

Но бывают случаи, когда положительное определение дать невозможно. Например, «точка есть то, что не имеет величины». Если в качестве ближайшего рода здесь взять всю совокупность геометрических образов и понятий, то такое определение будет в общем соразмерным. Но если ближайший род не определен, то и отрицательное понятие оказывается неопределенным. Например, к числу не имеющих величины могут быть отнесены также «душа», «истина», «добро», «справедливость» и т.п.

 

4. Определение должно быть ясным. Неясным является определение, в котором определяющее само нуждается в определении. Например, когда говорят, что «эксцентричность есть своеобразная идиосинкразия», то есть неизвестное пытаются определить через неизвестное.

 

Адекватное логическое определение не должно быть также метафорой. Например, «архитектура есть застывшая музыка», «лень есть мать всех пороков» и т.д. Но надо учесть, что это недопустимо только с формальной логической точки зрения. Иначе получится, что в науке вообще недопустима образная речь, — в некоторых случаях образ дает более ясное, короткое и верное пояснение, чем пространные формальные рассуждения.

 

Приемы, заменяющие определение. В науке мы не всегда можем сразу дать адекватное определение. Например, если ученые сталкиваются с неизвестным до того явлением и его надо предварительно как-то зафиксировать, то это явление пытаются прежде всего описать. Такой прием, заменяющий определение, называется описанием. Охарактеризуем приемы, заменяющие определение.

 

1.        Описание. Описание — это по возможности полное перечисление всех отличительных признаков данного явления. Например, «это растение, которое растет на каменистой почве в сухом климате при умеренной температуре, имеет листья средней величины круглой формы, цветет в мае, цветы небольшие, имеющие пять лепестков красного цвета» и т.д.

2.        Указание. Указание — это часто буквально указание пальцем. Например, преподаватель указывает пальцем на предмет, который находится перед ним на столе, и говорит: «этот прибор называется амперметр».

3.        Характеристика. При характеристике, в отличие от простого описания, приводятся характерные, или выдающиеся, признаки предмета или явления. Например, «научная работа требует колоссальных затрат умственной энергии». Характеристика, как правило, не может обойтись без образа, метафоры и даже гиперболы.

4.        Сравнение. Сравнение — это прием, когда значение одного понятия поясняется при помощи сравнения с другим понятием. Например, «распространение света аналогично распространению волн на поверхности воды».

5.        Различение. Это указание на различие, которое существует между данным понятием и другим, близким ему по смыслу. Например, мы говорим, что религия отличается от мифологии тем, что религия предполагает еще культ, то есть служение, почитание, которых нет в мифологии.

 

Деление понятия

 

Делением понятия называется логическая операция, при помощи которой по отношению к данному понятию как роду выделяют видовые понятия, сумма объемов которых равна объему родового, делимого, понятия. Например, все деревья можно разделить на лиственные и хвойные. Это и есть деление понятия «дерево» на понятия «хвойное дерево» и «лиственное дерево». Но не надо путать логическое деление понятия с физическим делением самого предмета. Например, дерево можно распилить и получатся дрова. Но путем логического деления понятия «дерево» мы никогда не получим понятие «дрова».

 

Деление понятия производится по некоторому основанию, которое называется основанием деления. Основанием деления является тот признак, который дает нам возможность разделить род на виды. Например, основанием деления деревьев на лиственные и хвойные является признак, связанный с формой листа, — лист или хвоя.

 

Одно и то же понятие можно делить по разным основаниям. То же понятие «дерево» можно делить не только на «хвойное дерево» и «лиственное дерево», но и на такие виды, как «твердые породы дерева» и «мягкие породы дерева». Точно так же треугольники можно делить на тупоугольные, прямоугольные и остроугольные по величине угла, а можно их делить по относительной величине сторон на равносторонние, равнобедренные и разносторонние.

 

Процесс деления можно продолжать и полученные от деления виды делить, в свою очередь, на подвиды. Например, понятие, полученное от деления понятия «дерево», а именно «лиственное дерево», можно делить на подвиды: «широколиственное дерево» и «узколиственное дерево».

 

Дихотомия. В процессе деления иногда употребляют специальный прием, который называется дихотомией, то есть делением пополам. Этот прием заключается в том, что понятие, подлежащее делению, мы делим на понятие, являющееся одним из видов, и на понятие, противоречащее полученному. Если мы в понятии «человек» выделим вид «славянин», то другим членом деления будет «не-славянин». Это деление тоже можно продолжать, и понятие «не-славянин» разделить на подвиды: «семиты» и «не-семиты». Последнее, в свою очередь, на понятия «негры» и «не-негры». Такое деление имеет то преимущество, что здесь не требуется единого основания деления, которое не всегда просто определить.

 

Правила деления. Возможные ошибки

 

1.Деление должно быть соразмерным. Это значит, что объем делимого понятия должен быть равен сумме объемов членов деления. Если при делении мы не перечислим всех видов, то сумма их объемов будет меньше объема делимого понятия, и мы будем иметь неполное деление. А если мы в объем делимого понятия введем виды, которые в нем не содержатся, то у нас получится деление слишком широкое, тоесть сумма объемов видов будет больше объема рода.

 

Возьмём, например, такое деление:

 



 

Это деление неполное, потому что здесь пропущен еще один член деления — прямоугольный треугольник.

 

Другой пример:

 



 

Сплав не является химическим элементом и оказывается здесь лишним членом деления, который делает объем членов деления в сумме больше объема делимого понятия.

 

2.Деление должно иметь одно основание. Довольно часто встречающаяся ошибка при делении заключается в том, что в процессе деления одно основание подменяется другим. Например: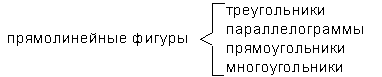

 



Здесь одновременно присутствуют три основания деления: число сторон, направление сторон, величина углов. Такое деление называется перекрестным.

 

Итак, при делении должно быть выдержано единое основание. Но это не значит, что после того, как произведено полное деление по одному основанию, мы не можем приступить к новому делению уже одного из полученных видов на подвиды уже по другому основанию. Например,

 



 

Здесь после того, как мы разделили треугольники по величине угла на тупоугольные, прямоугольные и остроугольные, мы делим уже остроугольные треугольники по величине сторон на равносторонние, равнобедренные и разносторонние.

 

3.Члены деления должны исключать друг друга. Например, «книги бывают французские, немецкие и словари». Это деление неверно, потому что словари бывают и немецкие и французские, а среди немецких и французских книг есть и словари. То есть члены деления не исключают друг друга.

4.Деление должно быть непрерывным. Это требование заключается в том, что при делении какого-нибудь понятия нужно переходить к ближайшему низшему роду, иначе получается так называемый скачок в делении. Если мы понятие «природа» разделим на «животных», «растения» и «минералы», то в этом делении делается скачок от «природы» к «животным» и «минералам». «Природу» следует разделить сначала на «живую» и «неживую», а уже затем «живую» на «растения» и «животные».

 

Это все о понятии. Теперь мы должны перейти к суждению.

 

Контрольные вопросы:

 

1.Когда и кем была основана логика?

2.Что такое понятие как форма мышления?

3.Чем понятие отличается от представления?

4.Что такое абстрагирование?

5.Что такое признаки, какова разница между существенными и отличительными признаками?

6.Что такое термин?

7.Что такое объем понятия?

8.Что такое содержание понятия?

9.Что означает закон обратного соотношения объема и содержания понятия?

10.Что такое род и вид понятия?

11.Что такое «древо Порфирия»?

12.Что такое ближайший род?

13.Что такое ограничение и обобщение понятия?

14.Что такое категория?

15.Какие бывают отношения между понятиями по объему?

16.Что такое определение понятия?

17.Какие требования предъявляются к определению понятия?

18.Какие существуют приемы, заменяющие определенные понятия?

19.Что такое деление понятия?

20.Каковы правила деления?

ЛЕКЦИЯ 2. СУЖДЕНИЕ

 

Суждение есть мысль, в которой что-то утверждается или отрицается и которой можно приписать значения «истинно» или «ложно». Например, суждениями являются предложения «эта роза красная», «на Марсе нет жизни», «этот поступок не является благородным» и т.д.

Простые суждения

 

Простым называется суждение, никакая часть которого не является суждением. Например, если суждение «эта роза красная» — простое суждение, то суждение «эта роза красная и пахучая» уже является сложным, потому что оно состоит из двух простых суждений «эта роза красная» и «эта роза пахучая».

 

Всякое простое суждение состоит из трех частей: субъекта, предиката и глагола-связки «есть» («не есть).

 

Субъект суждения это то, о чем идет речь. Это логическое подлежащее.

 

Предикат суждения это то, что утверждается о субъекте. Это логическое сказуемое.

 

Глагол-связка указывает на принадлежность данного предиката данному субъекту.