Логика. 0011230_ЛОГИКА. Тестирующая система
 Скачать 410 Kb. Скачать 410 Kb.
|
Логическая форма простого суждения «S есть P», где S — субъект, P — предикат.Виды сужденийСуждения делятся на виды по качеству и по количеству. Качество суждения зависит от того, утверждается что-либо в суждении или отрицается. Соответственно, по качеству суждения делятся на утвердительные и отрицательные. По количеству суждения делятся в зависимости от того, утверждается в суждении что либо обо всех предметах данного рода или только о некоторых. Те суждения, в которых утверждается нечто обо всех предметах данного рода, называется общим. А те суждения, в которых что-то утверждается только о некоторых предметах данного рода, называются частными. Например, все суждения в науке, выражающие закон, являются общими суждениями: «всякое тело падает на Землю с ускорением 9,8 м/сек2», «во всяком треугольнике сумма внутренних углов равна 180 градусам» и т.д. Частные суждения начинаются, как правило, словом «некоторые», или «иногда», «часто» и т.д. В пределе это суждение о конкретном единичном случае. Например, «некоторые люди имеют черный цвет кожи», «в средних широтах часто идут дожди», «планеты солнечной системы иногда движутся по неправильным орбитам» и т.п. Но суждения утвердительные могут быть и общими, и частными, а частные — утвердительными и отрицательными. Таким образом, всего по качеству и количеству будет четыре вида суждений, которые обозначаются большими латинскими буквами A, I, E, O. Буквы взяты из латинских слов affirmo и nego. Первые две гласные из слова affirmo, что значит «утверждаю», A и I означают общеутвердительное и частноутвердительное суждения, а две гласные слова nego, что значит «отрицаю», Е и О обозначают общеотрицательное и частноотрицательное суждения. Сводная таблица получается такая: (А) Все S есть Р, общеутвердительное суждение; (I) Некоторые S есть Р, частноутвердительное суждение; (Е) Ни одно S не есть Р, общеотрицательное суждение; (О) Некоторые S не есть Р, частноотрицательное суждение. Распределенность терминов в суждении Терминами суждения называются понятия, выражающие субъект и предикат суждения. Например, в суждении «эта роза красная» терминами являются «эта роза» и «красная». Термин называется распределенным, если его объем полностью входит в объем другого термина, или не входит в него никакой частью своего объема. Например, термин А распределен относительно термина В, если имеет место один из двух случаев:  Термин не распределен в суждении, если его объем не полностью входит в объем другого термина, а только частично. Например, термин А не распределен относительно термина В, если имеет место случай  В общеутвердительном суждении (А), «все S есть Р» субъект распределен, предикат не распределен. На кругах Эйлера это выглядит так: 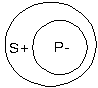 Значок «+» означает «распределен», значок «-» — «не распределен». В общеотрицательных суждениях (Е) «ни одно S не есть Р» субъект распределен и предикат распределен: 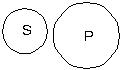 В частноутвердительных суждениях (I) «некоторые S есть Р» субъект не распределен и предикат не распределен:  В частноотрицательных суждениях (О) «некоторые S не есть Р» субъект не распределен, предикат распределен:  Этот случай представляет некоторые трудности для понимания. Следует обратить внимание на то, что в данном случае «некоторые S» говорит о том, что S не всем своим объемом входит в Р, но Р никакой частью своего объема не входит в объем «некоторых S». Например, если говорится «некоторые люди побывали на Луне», то это значит, что термин «не побывавшие на Луне» только частично входит в объем людей, побывавших на Луне. А термин «побывавшие на Луне» никакой частью своего объема не входит в объем термина «не побывавшие на Луне». Распределенность терминов в суждении можно представить в виде таблицы:
Из таблицы видно, что субъект всегда распределен в общих суждениях и не распределен в частных; предикат распределен в отрицательных и не распределен в утвердительных суждениях. Отношения между суждениями. Логический квадрат Под отношениями в данном случае имеются в виду отношения между суждениями разного вида, но имеющими один и тот же субъект и один и тот же предикат. Например, суждения «все люди смертны» и «некоторые люди бессмертны». Каково может быть отношение между двумя такими суждениями? Понятно, что если суждение «все люди смертны» истинно, то отсюда следует, что суждение «некоторые люди бессмертны» — ложно. Именно такого рода отношения и изучает логика: она изучает зависимость истинности или ложности суждения одного вида от истинности или ложности суждения, или суждений, другого вида. Например, из истинности суждения «все люди смертны» следует, очевидно, истинность суждения «некоторые люди смертны». Но если бы суждение «все люди смертны» было ложным, то отсюда следовала бы истинность суждения «некоторые люди бессмертны». Но это не зависит от конкретного содержания суждений. Поэтому эти отношения и можно выразить в общем виде. Если истинно «Все S есть Р», то истинно «Некоторые S есть Р». Или просто, А I, и т.д. Для наглядного представления всех возможных отношений между всеми четырьмя видами суждений была в свое время придумана схема под названием «логический квадрат». Его придумал римский христианский философ Боэций (480- 526 гг. н.э.). Этот «квадрат» выглядит следующим образом.  Символы А, Е, I, О, обозначающие четыре вида суждений, располагаются по углам «квадрата». Диагонали и стороны квадрата означают все возможные отношения между всеми видами суждений. Отношения по вертикальным сторонам квадрата называются отношением подчинения. Суждение вида А подчиняет себе суждение вида I, но не наоборот. То же самое и для суждений вида Е и О. Отношение между суждениями А и Е называется отношением противоположности. Суждение вида А утверждает нечто обо всех, а суждение вида Е отрицает нечто обо всех. И эти два суждения не могут быть оба истинными, но могут быть оба ложными. Например, если взять суждения «все студенты данной группы сдали экзамен по логике» и «ни один студент данной группы не сдал экзамен по логике», то они могут быть оба ложными, если некоторые студенты сдали экзамен по логике, а некоторые не сдали. Отношение между суждениями вида I и О называется отношением частичной совместимости. Иногда такие суждения называют подпротивными. Эти суждения могут быть одновременно истинными, но не могут быть одновременно ложными. Если возьмем суждения «некоторые студенты данной группы сдали экзамен по логике» и «некоторые студенты данной группы не сдали экзамен по логике», то эти суждения, понятно, могут быть оба истинными, но не могут быть оба ложными, и когда одно из них истинно, то другое обязательно ложно, и наоборот, если одно из них ложно, то другое обязательно истинно. |
