Задание 5
Дан треугольник АВС. Найти: а) площадь треугольника; б) длину высоты, опущенной на сторону АС.
№
|
А
|
В
|
С
|
5.1
|
(2; 2; 4)
|
(3; 1; 0)
|
(1; 0; 2)
|
5.2
|
(1; 1; -4)
|
(-2; -2; 4)
|
(0; -1; 2)
|
5.3
|
(-1; -1; 0)
|
(2; 2; 0)
|
(0; 1; -2)
|
5.4
|
(-2; 2; 4)
|
(1; -1; 4)
|
(-1; 0; 2)
|
5.5
|
(1; -1; -4)
|
(-2; 2; 4)
|
(0; 1; 2)
|
5.6
|
(-2; 0; -1)
|
(-1; 2; -3)
|
(0; 1; 1)
|
5.7
|
(2; 4; 0)
|
(1; 0; 1)
|
(0; 2; -1)
|
5.8
|
(3; -2; 0)
|
(3; 1; -3)
|
(1; 0; -1)
|
5.9
|
(1; 2; 0)
|
(0; 4; -2)
|
(3; 4; 1)
|
5.10
|
(-1; 0; 2)
|
(1; 2; 3)
|
(1; -1; 0)
|
5.11
|
(-2; 0; 1)
|
(0; 1; 3)
|
(0; -2; 0)
|
5.12
|
(2; 0; -1)
|
(3; 2; 1)
|
(0; 2; -2)
|
5.13
|
(2; 1; 0)
|
(1; 3; 2)
|
(4; 0; 2)
|
5.14
|
(-2; -1; 0)
|
(-3; 1; 2)
|
(0; 1; -1)
|
5.15
|
(1; 0; -1)
|
(-2; 0; 2)
|
(0; -2; 1)
|
5.16
|
(0; -2; -1)
|
(2; 2; -5)
|
(-4; 2; 1)
|
5.17
|
(1; 2; 0)
|
(5; 4; -4)
|
(3; 6; 4)
|
5.18
|
(-1; -2; 0)
|
(1; 2; 4)
|
(-5; -4; 4)
|
5.19
|
(1; 0; -2)
|
(5; 2; 2)
|
(-1; -4; 2)
|
5.20
|
(-1; 1; 0)
|
(3; -1; 4)
|
(-3; 5; 4)
|
5.21
|
(0; 2; 1)
|
(-4; 4; 5)
|
(2; -2; 5)
|
5.22
|
(-1; 0; -2)
|
(1; 4; -6)
|
(3; 1; 2)
|
5.23
|
(1; -2; 0)
|
(3; -6; 4)
|
(5; 2; 2)
|
5.24
|
(1; 1; 0)
|
(5; 3; -4)
|
(5; -3; 2)
|
5.25
|
(-1; 2; 0)
|
(3; 6; 2)
|
(-3; 6; -4)
|
5.26
|
(0; 1; -1)
|
(-2; 5; 3)
|
(4; -3; -3)
|
5.27
|
(-2; 1; 0)
|
(0; 5; -4)
|
(-6; 5; 2)
|
5.28
|
(0; -1; -2)
|
(-4; 3; 0)
|
(2; 3; -6)
|
5.29
|
(2; -1; 0)
|
(0; 3; 4)
|
(6; 3; -2)
|
5.30
|
(1; -1; -1)
|
(3; 3; 3)
|
(-3; 3; -3)
|
Задание 6
Даны координаты вершин тетраэдра ABCD. Найти: а) объём тетраэдра; б) длину высоты, опущенной на основание АВС.
№
|
А
|
В
|
С
|
D
|
6.1
|
(0; 1; -2)
|
(2; 1; -1)
|
(1; 1; -4)
|
(3; -1; -3)
|
6.2
|
(-1; 3; 2)
|
(-1; 5; 3)
|
(1; 4; -4)
|
(2; 2; 5)
|
6.3
|
(-1; 0; -3)
|
(0; 2; -3)
|
(1; -1; 3)
|
(2; 1; 0)
|
6.4
|
(2; -1; 1)
|
(3; -1; 3)
|
(4; 1; 0)
|
(1; 3; 2)
|
6.5
|
(-2; 0; 1)
|
(2; 2; 0)
|
(-2; 1; 3)
|
(2; -1; 2)
|
6.6
|
(3; 2; -1)
|
(5; 3; 1)
|
(2; 4; -1)
|
(4; 3; 4)
|
6.7
|
(0; -1; 3)
|
(2; 1; 4)
|
(-1; -1; 5)
|
(3; 4; 1)
|
6.8
|
(1; 2; -1)
|
(-1; 4; 0)
|
(1; 1; 1)
|
(2; 3; 2)
|
6.9
|
(1; -2; 0)
|
(2; 0; 0)
|
(-1; -1; 2)
|
(2; 1; -1)
|
6.10
|
(2; -1; 3)
|
(3; 1; 5)
|
(0; 1; 4)
|
(4; 1; 2)
|
6.11
|
(3; -1; 0)
|
(-3; 0; 2)
|
(1; -3; 1)
|
(1; 2; -1)
|
6.12
|
(1; 2; -3)
|
(-1; 1; 3)
|
(2; 0; -3)
|
(2; -1; 0)
|
6.13
|
(2; -1; 3)
|
(0; -1; 2)
|
(1; 1; 5)
|
(3; 2; 1)
|
6.14
|
(3; -2; 1)
|
(3; -4; 0)
|
(-3; -1; -1)
|
(1; 0; 2)
|
6.15
|
(2; 3; -1)
|
(1; 1; 1)
|
(4; 2; -1)
|
(3; 2; 3)
|
6.16
|
(-3; 1; 2)
|
(-4; -1; 0)
|
(-5; 1; 3)
|
(1; -4; 1)
|
6.17
|
(1; 3; -2)
|
(-1; 2; -4)
|
(1; 5; -3)
|
(-4; 1; 0)
|
6.18
|
(0; 1; 2)
|
(1; 2; -2)
|
(-1; 2; 2)
|
(1; -1; 3)
|
6.19
|
(1; 1; -1)
|
(2; 1; 0)
|
(0; -1; 0)
|
(-1; 2; 1)
|
6.20
|
(-2; 1; 1)
|
(2; 2; 2)
|
(-2; 0; 2)
|
(0; 3; -1)
|
6.21
|
(1; -3; 2)
|
(0; -4; -2)
|
(2; -4; 2)
|
(-1; 0; 4)
|
6.22
|
(1; 0; 2)
|
(0; 0; 1)
|
(2; 1; 1)
|
(2; -3; -1)
|
6.23
|
(1; -1; 1)
|
(-1; -2; 0)
|
(2; 0; 0)
|
(-2; 3; 3)
|
6.24
|
(1; -2; 1)
|
(2; -1; -1)
|
(-2; -3; 1)
|
(3; 1; -3)
|
6.25
|
(1; 2; -3)
|
(2; -2; -2)
|
(2; 2; -4)
|
(-2; -2; -1)
|
6.26
|
(2; 1; 0)
|
(-2; 2; 1)
|
(2; 2; -1)
|
(-3; 0; 2)
|
6.27
|
(-1; 1; 1)
|
(-2; 0; -1)
|
(-2; 2; 2)
|
(2; 2; -4)
|
6.28
|
(1; 1; -2)
|
(0; -1; -3)
|
(0; 1; -1)
|
(-1; 2; 1)
|
6.29
|
(2; 1; -3)
|
(-2; 0; -4)
|
(2; 0; -2)
|
(1; -1; -1)
|
6.30
|
(-1; 1; 2)
|
(1; 2; 2)
|
(0; -1; -2)
|
(2; -2; 0)
|
Задание 7
7.1. Сила  приложена к точке А. Определить момент этой силы относительно точки N, если: приложена к точке А. Определить момент этой силы относительно точки N, если:
а)  = (2; 3; 1); А(1; 1; 1); N(-1; 2; 4); = (2; 3; 1); А(1; 1; 1); N(-1; 2; 4);
б)  = (-2; 3; 4); А(-1; 1; -1); N(0; 0; 0); = (-2; 3; 4); А(-1; 1; -1); N(0; 0; 0);
в)  = (2; 1; -1); А(1; 1; 4); N(-1; 2; 2); = (2; 1; -1); А(1; 1; 4); N(-1; 2; 2);
г)  = (3; 2; -4); А(2; -1; 1); N(0; 0; 0); = (3; 2; -4); А(2; -1; 1); N(0; 0; 0);
д)  = (-1; 3; 2); А(-2; 1; 0); N(1; 1; -1). = (-1; 3; 2); А(-2; 1; 0); N(1; 1; -1).
7.2. Даны три силы  , ,  , ,  , приложенные к точке С. Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки А, если: , приложенные к точке С. Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки А, если:
а)  (2; -1; -3), (2; -1; -3), 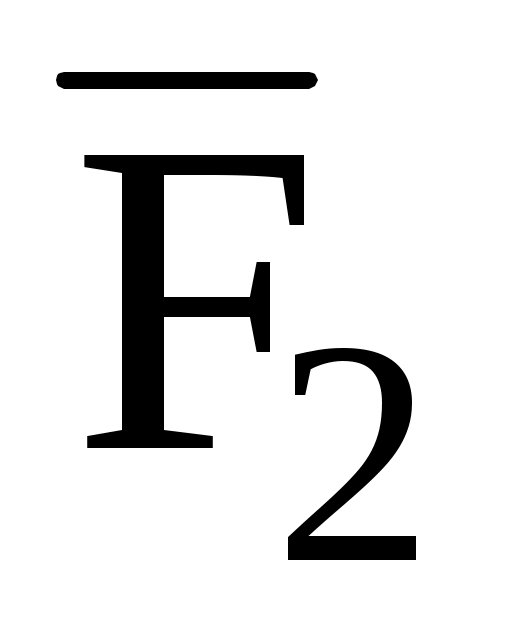 (3; 2; -1), (3; 2; -1), 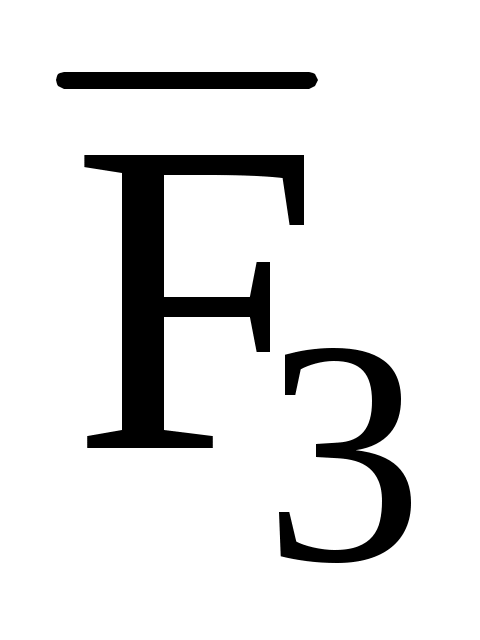 (-4; 1; 3), С(-1; 4; -2), А(2; 3; -1); (-4; 1; 3), С(-1; 4; -2), А(2; 3; -1);
б)  (1; 1; 1), (1; 1; 1), 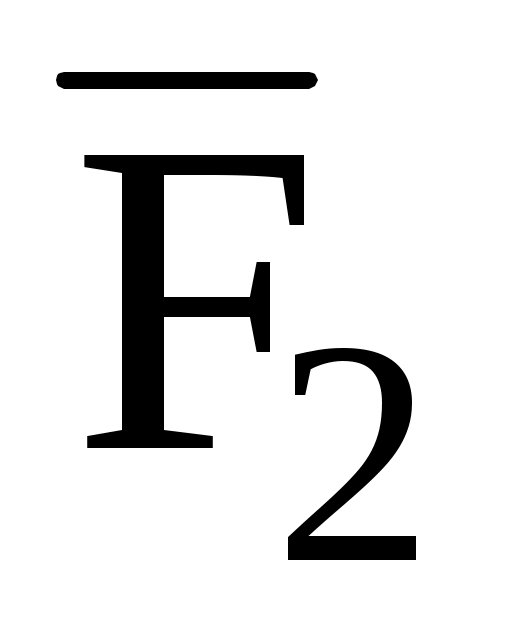 (-2; -3; 1), (-2; -3; 1), 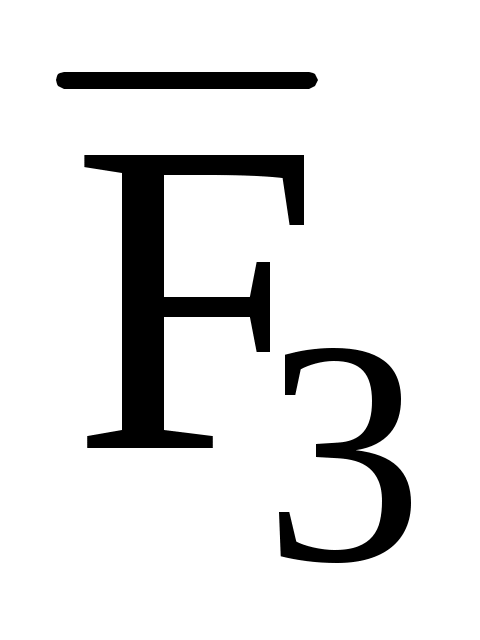 (1; -2; 1), С(2; 1; 2), А(0; -1; -1); (1; -2; 1), С(2; 1; 2), А(0; -1; -1);
в)  (1; 0; -2), (1; 0; -2), 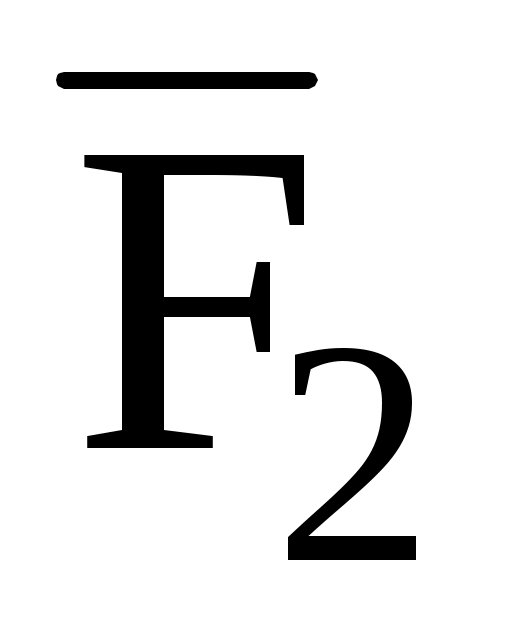 (2; 2; 3), (2; 2; 3), 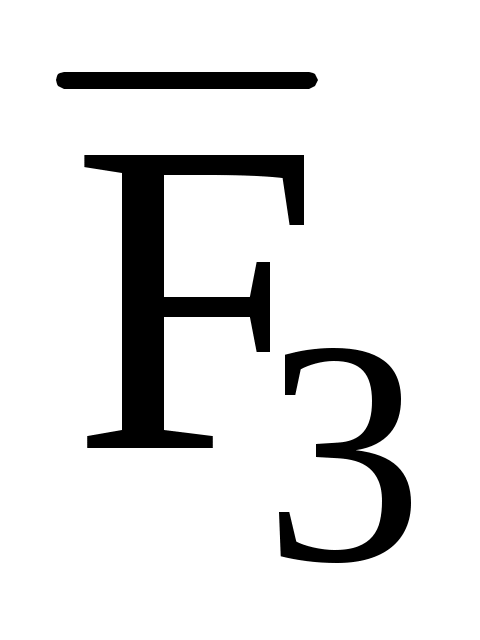 (0; 1; -1), С(0; 2; -3), А(-1; 1; 2). (0; 1; -1), С(0; 2; -3), А(-1; 1; 2).
7.3. Проверить, что векторы 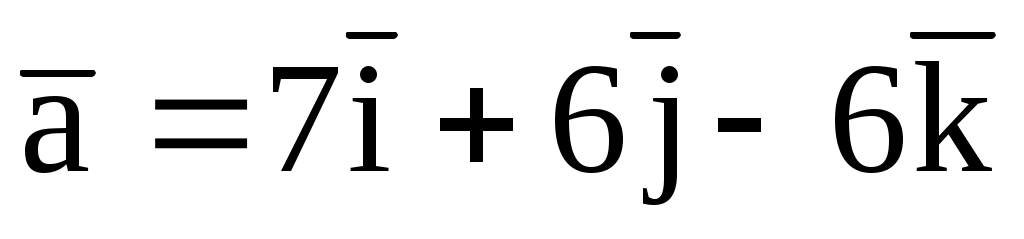 и и 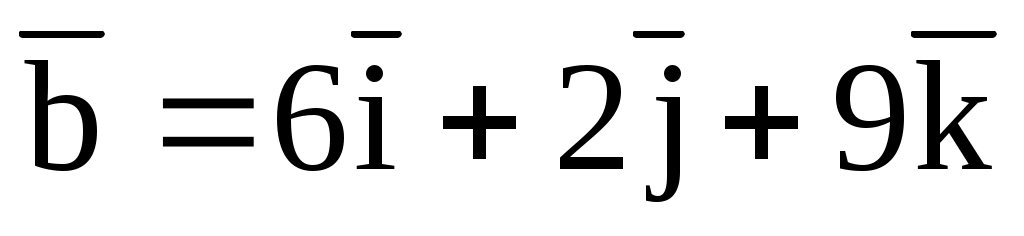 могут быть взяты за рёбра куба. Найти третье ребро куба. могут быть взяты за рёбра куба. Найти третье ребро куба.
7.4. Даны векторы  = (2; -3; 1), = (2; -3; 1),  = (-3; 1; 2), = (-3; 1; 2), 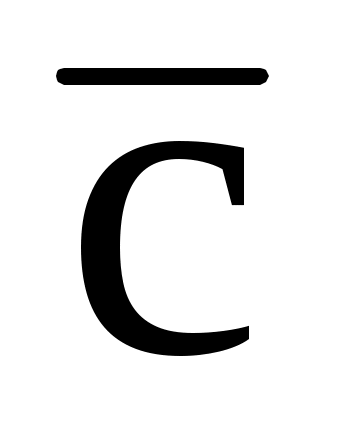 = (1; 2; 3). Вычислить = (1; 2; 3). Вычислить 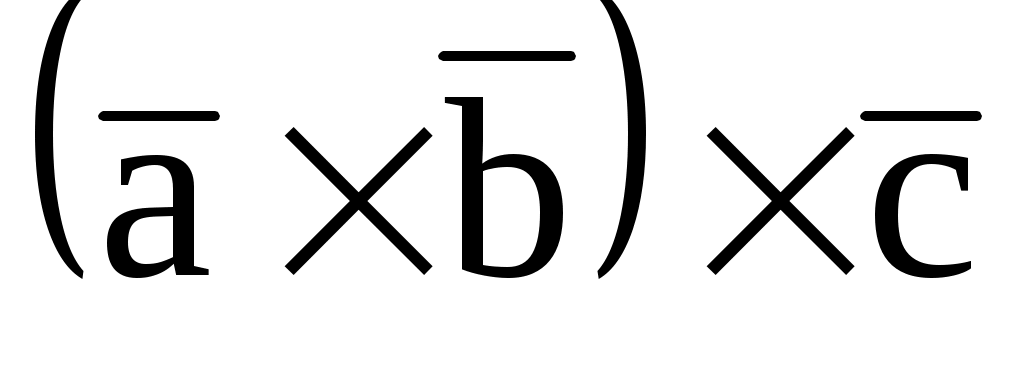 и и 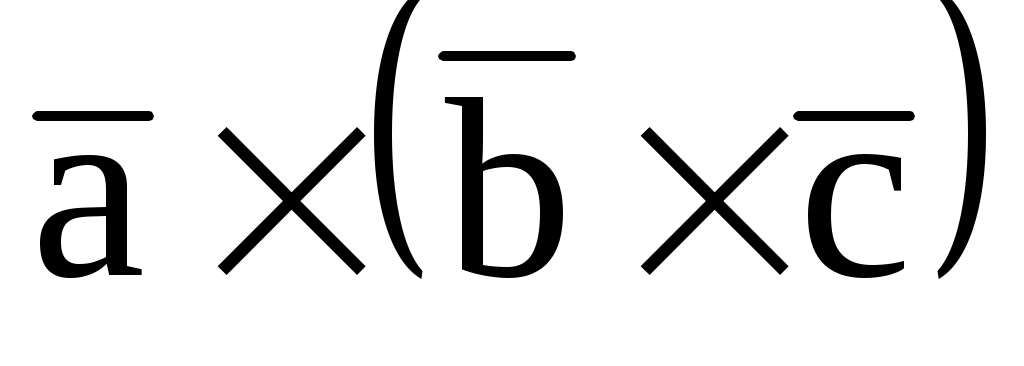 . .
7.5. Даны точки A, B, C, D. При каком значении "t" тройка векторов 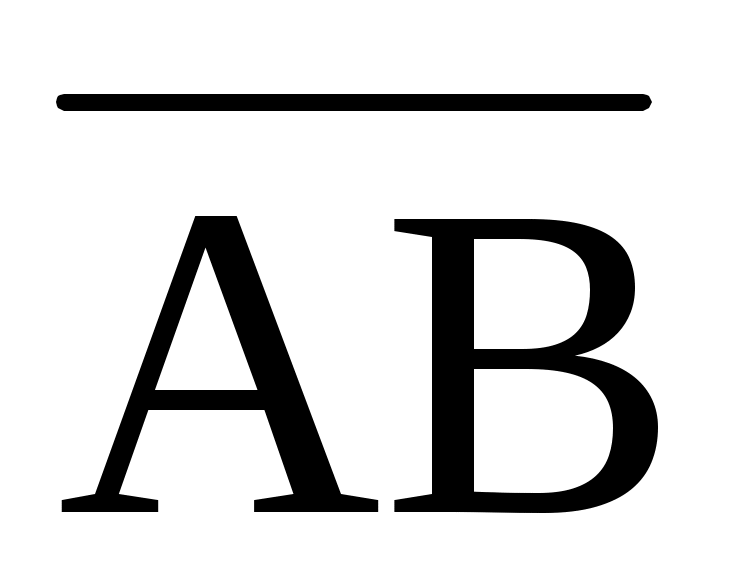 , , 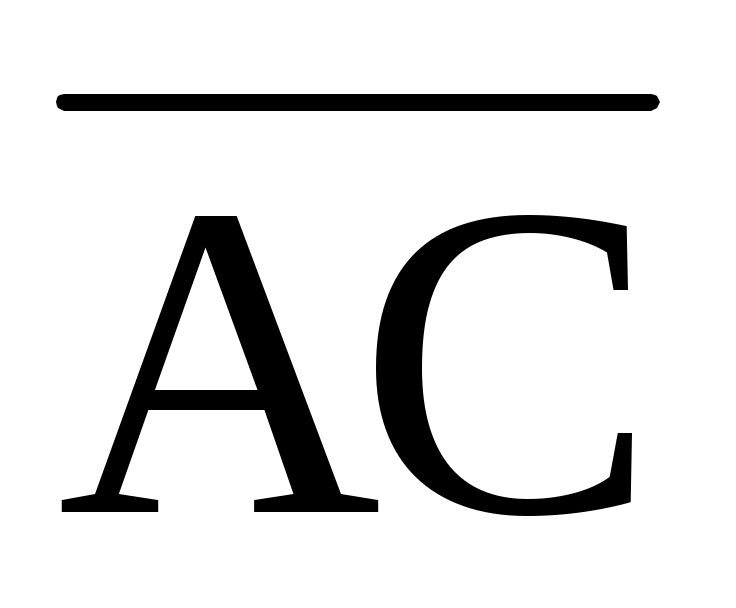 , ,  будет: будет:
а) левой, если А(1; -2; 0), В(3; t; -2), С(0; 1; 5), D(2; 2; -1);
б) правой, если А(3; -1; 2), В(2; 2; 0), С(2t; 1; 3), D(0; -1; 3).
7.6. Проверить, лежат ли в одной плоскости точки A, B, C, и D:
а) А(-1; 2; 1), В(0; 1; -2), С(1; 3; -2) и D(2; 4; -3);
б) А(-1; 2; 1), В(-7; 0; -3), С(4; -1; 2) и D(-2; 1; 0).
7.7. При каком значении t точки A, B, C, и D лежат в одной плоскости, если:
а) А(2; 0; -1), В(1; 1; 0), С(0; -1; t) и D(-1; 2; 2);
б) А(-1; 3; 2), В(2t; -1; 1), С(t; 2; 0) и D(1; 1; 1).
7.8. При каком значении t компланарны векторы  , ,  и и 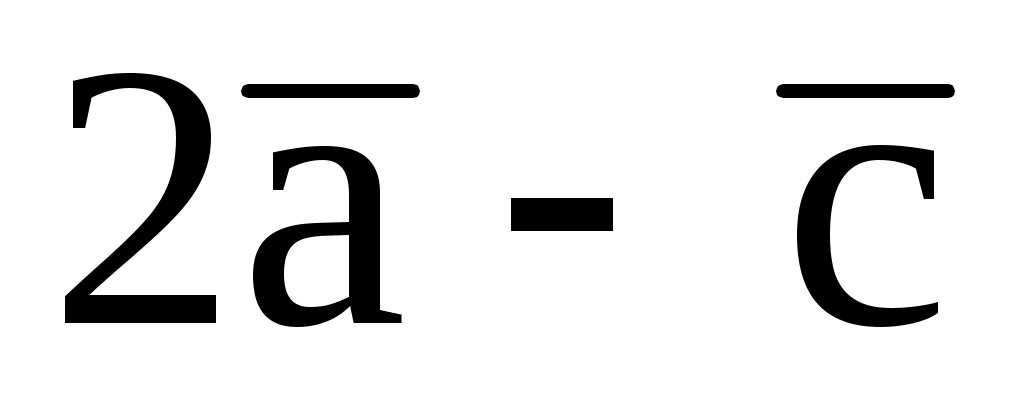 , если: , если:
а)  = (2; 1; -1), = (2; 1; -1),  (1; 2t; -1), (1; 2t; -1), 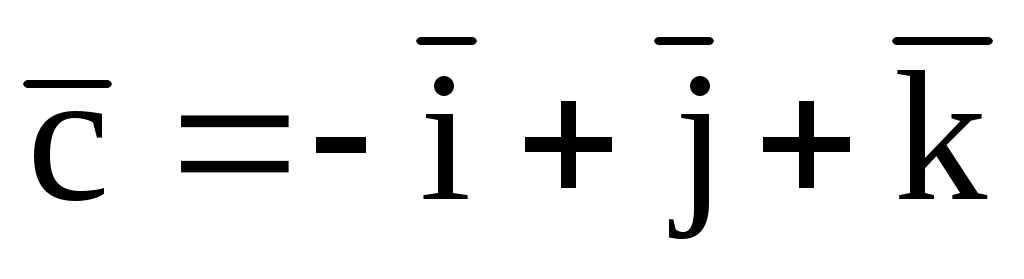 ; ;
б)  , ,  (1; 1; 0), (1; 1; 0), 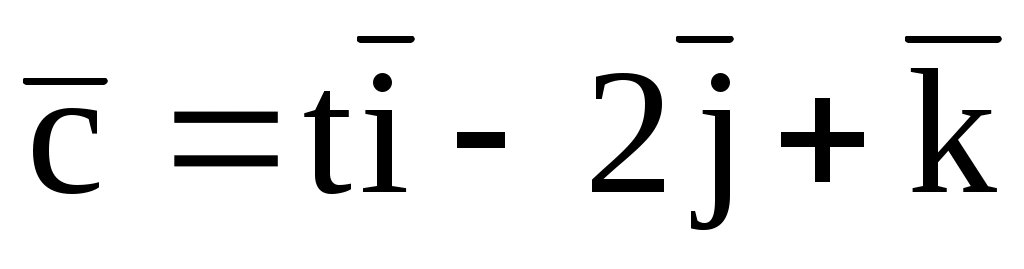 . .
7.9. Найти 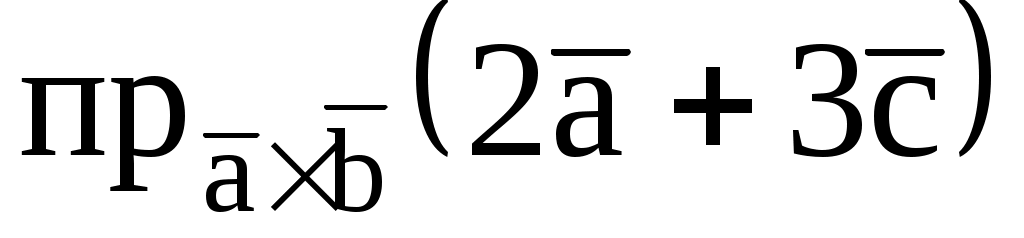 , если , если  = (1; 1; -1), = (1; 1; -1), 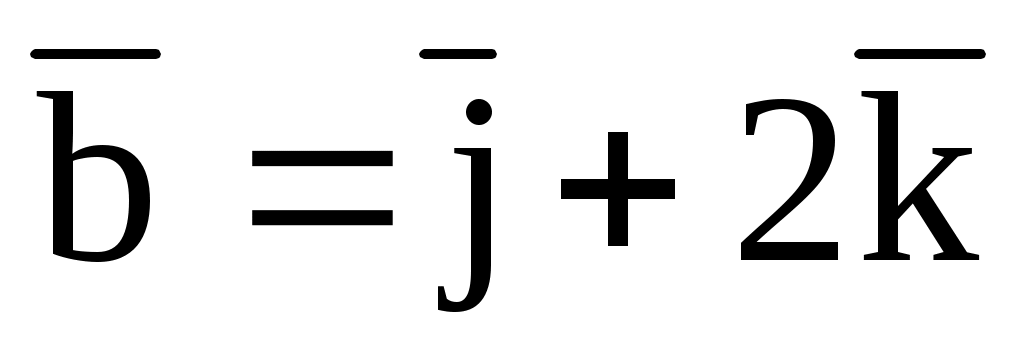 , , 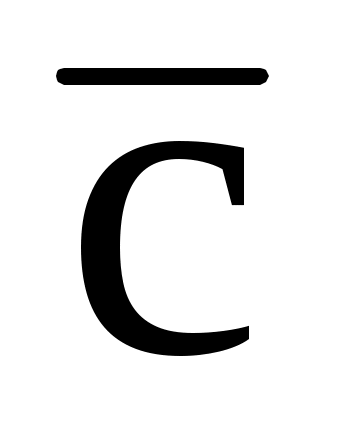 = (-1; 0; 1). = (-1; 0; 1).
7.10. Найти 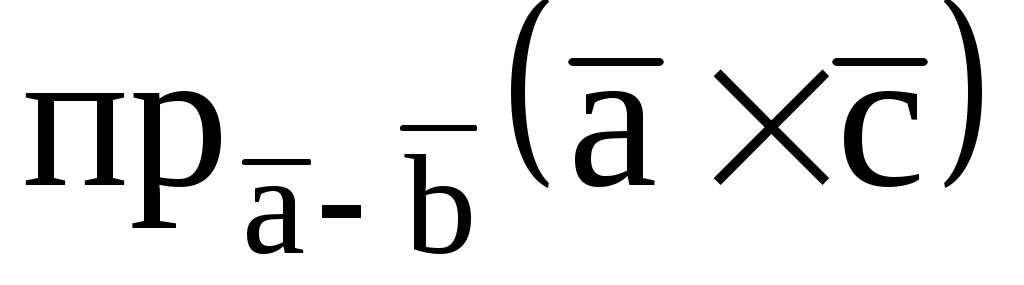 , если , если 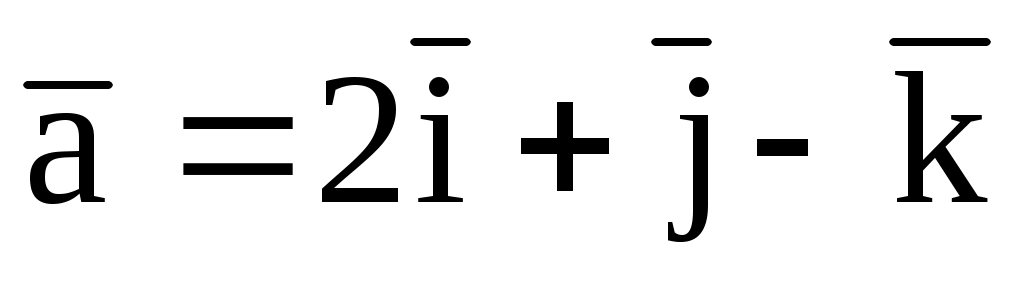 , ,  = (1; 2; 3), = (1; 2; 3), 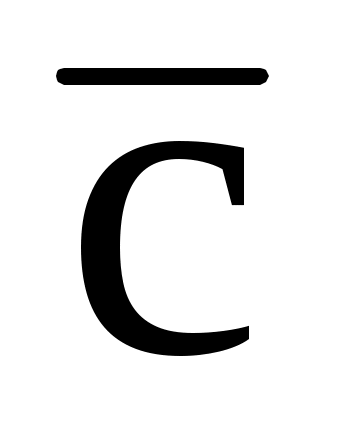 = (-1; 0; 2). = (-1; 0; 2).
7.11. При каком значении m векторы  (1; m; -1), (1; m; -1),  (2; 1; 3) и (2; 1; 3) и 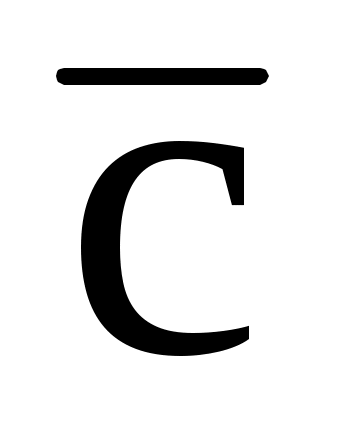 (-5; -1; 0) удовлетворяют соотношению (-5; -1; 0) удовлетворяют соотношению  ? ?
7.12. Объём тетраэдра ABCD равен V. Найти координаты вершины D, если:
а) V = 2; А(2; 1; 3), В(3; 3; 2), С(1; 2; 4), DOz;
б) V = 3; А(1; 2; 3), В(3; 2; 1), С(2; 3; 1), DOx;
в) V = 5; А(2; 1; -1), В(3; 0; 1), С(2; -1; 3), DOy.
7.13. При каком значении m 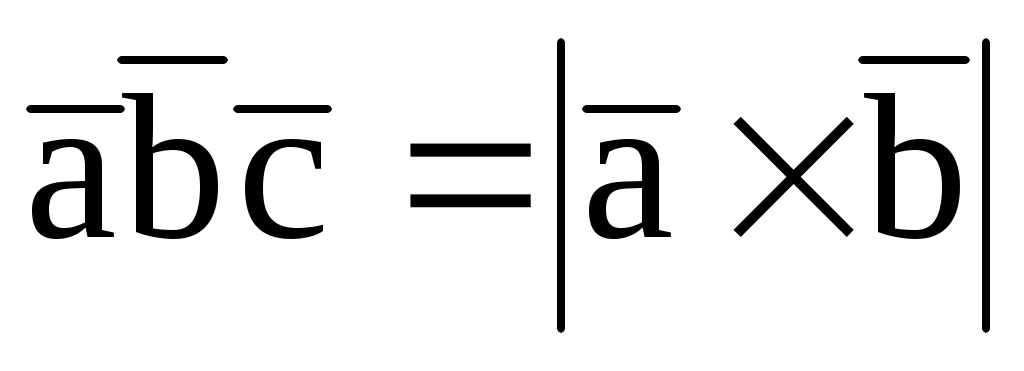 , если , если  = (2; -2; -3), = (2; -2; -3),  = (4; 0; 6), = (4; 0; 6), 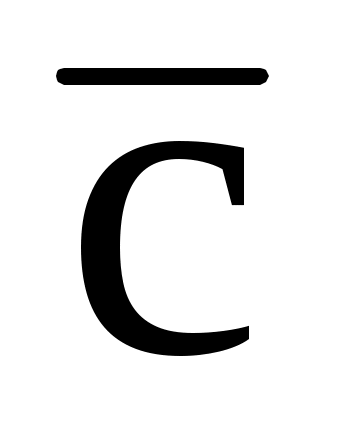 = (m; 1; -1). = (m; 1; -1).
7.14. При каком значении m 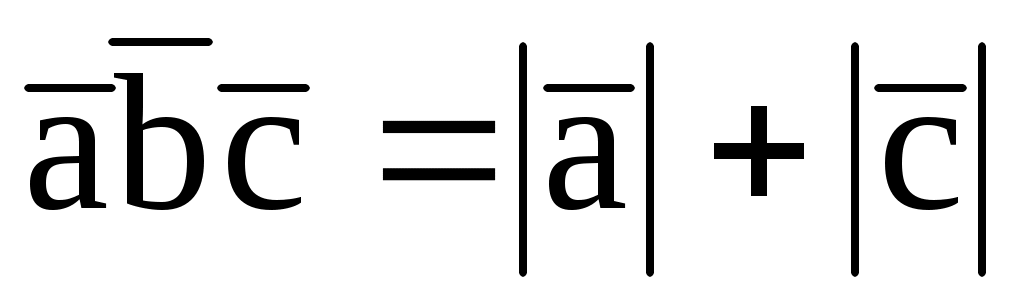 , если , если  (1; 2; -2), (1; 2; -2),  (m; -1; 1), (m; -1; 1),
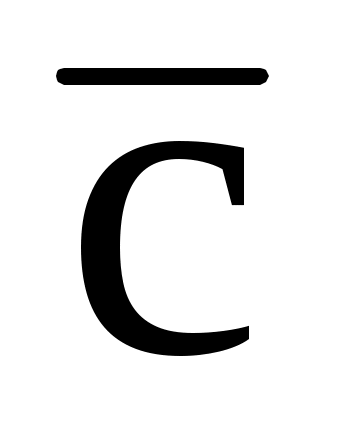 (-6; 2; 6) (-6; 2; 6)
7.15. При каком значении m тройка векторов  (3; 1; -1), (3; 1; -1),  (-1; m; 3), (-1; m; 3),
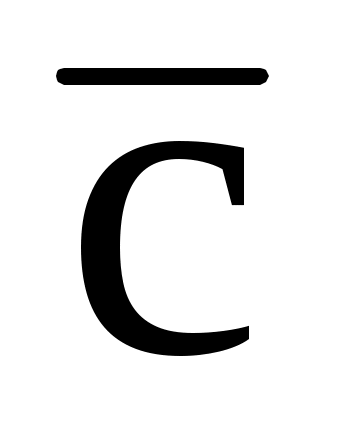 (2; 2; -2) будет левой и объём параллелепипеда, на них построенного, равен 8 ед3? (2; 2; -2) будет левой и объём параллелепипеда, на них построенного, равен 8 ед3?
7.16. При каком значении m 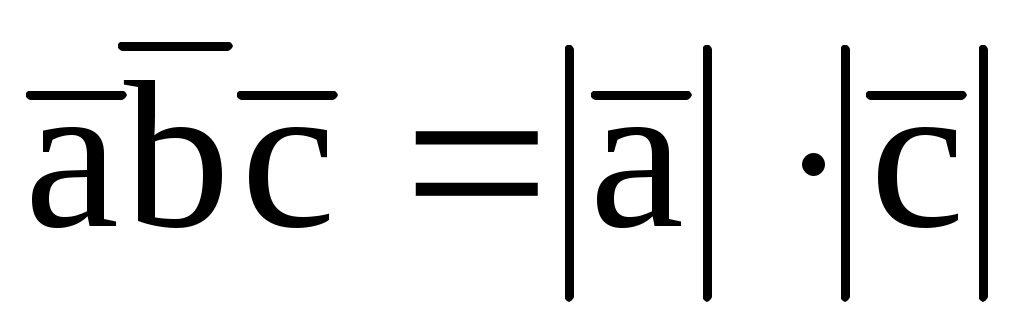 , если , если  = (2; 2; -1), = (2; 2; -1),  (-1; 3; m), (-1; 3; m), 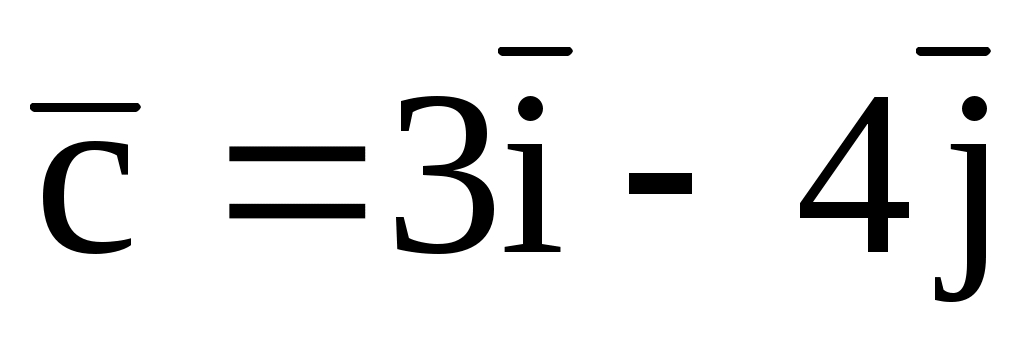 . .
7.17. Векторы 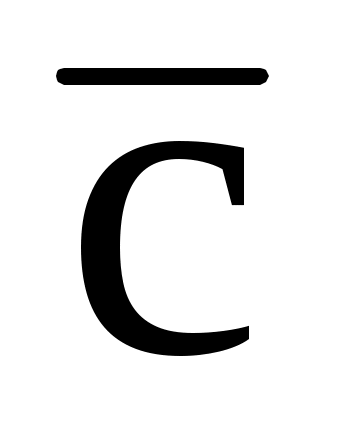 (3; 3; -4) и (3; 3; -4) и 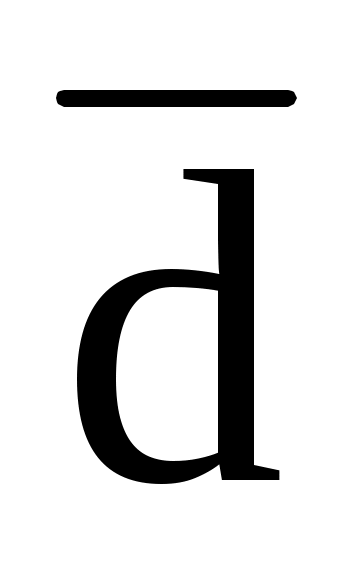 (-1; 1; 2) являются диагоналями параллелограмма, построенного на векторах (-1; 1; 2) являются диагоналями параллелограмма, построенного на векторах  и и  . Найти векторы . Найти векторы  , ,  и площадь параллелограмма. и площадь параллелограмма.
7.18. Найти единичный вектор, параллельный вектору 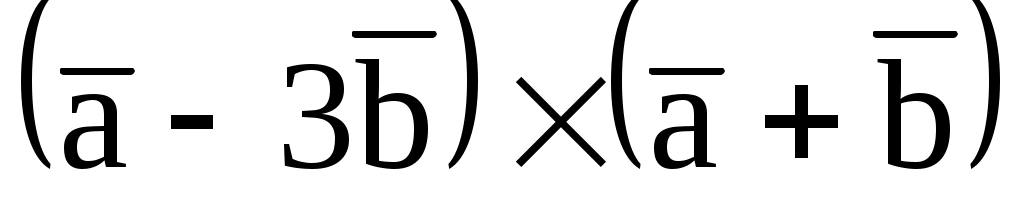 , если , если  = (2; -1; 3), = (2; -1; 3),  = (1; 1; 2). = (1; 1; 2). |
 Скачать 1.31 Mb.
Скачать 1.31 Mb.