Типовое расчётное задание
Векторная алгебра и её приложения к аналитической геометрии
Составитель Сахарова Л.В.
Задание 1
1.1. Найти координаты вектора  , коллинеарного вектору , коллинеарного вектору  и противоположно направленного, если и противоположно направленного, если
а)  = (-2; 5; 4); = (-2; 5; 4); 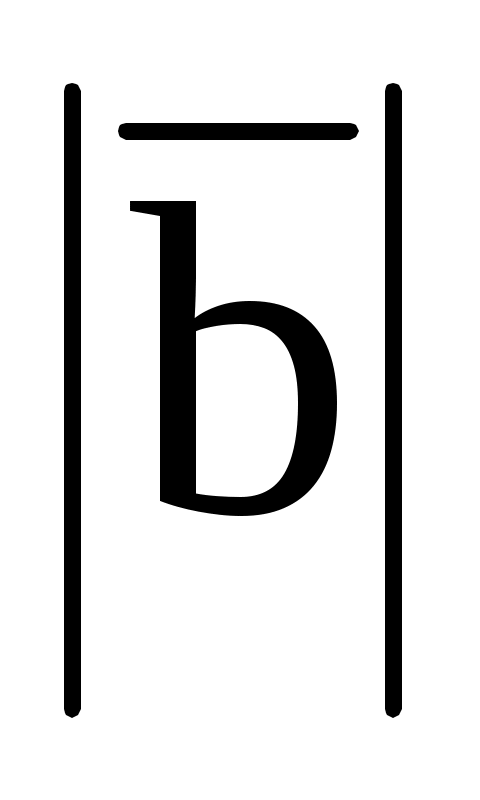 = = 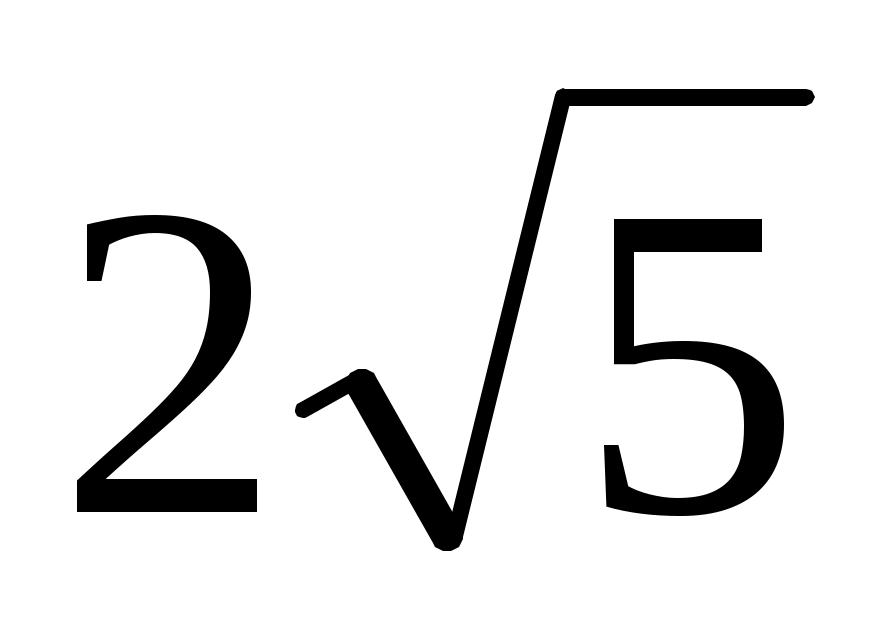 ; ;
б)  = (6; -6; 3); = (6; -6; 3); 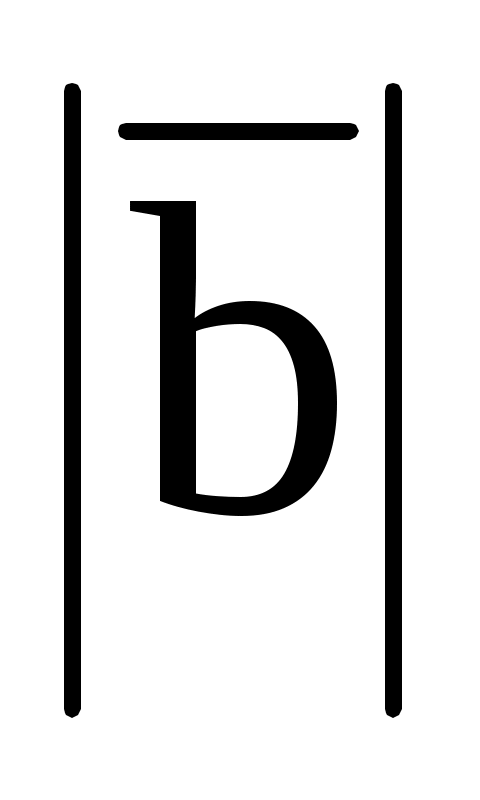 = 45; = 45;
в)  = (12; -3; -4); = (12; -3; -4); 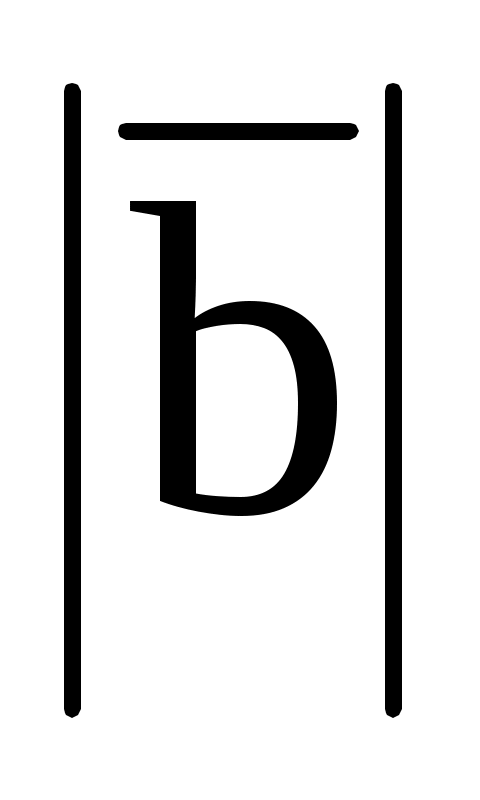 = 52. = 52.
1.2. На оси ординат найти точку К, равноудалённую от точек А(1; -4; 7) и В(5; 6; -5).
1.3. Даны две смежные вершины параллелограмма А(3; 3; -1) и В(-1; 5; 3) и точка О(2; -1; 4) пересечения диагоналей. Найти координаты двух других вершин.
1.4. Точки А(1; 0; 2), В(3; 1; 1) и С(-2; 3; -1) являются последовательными вершинами параллелограмма. Найти длины его диагоналей.
1.5. Даны три последовательные вершины параллелограмма: А(2; 1; -2),
В(-3; 5; 0) и С(4; -1; 6). Найти координаты четвёртой вершины Д.
1.6. Даны три последовательные вершины правильного 6-угольника: А(2; 1; -1), В(-3; 2; 2), С(1; 3; 6). Найти остальные его вершины.
1.7. На оси Oz найти точку К, равноудалённую от точек А(7; -4; 1) и
В(-5; 6; 5).
1.8. Зная одну из вершин треугольника А(3; 1; -1) и векторы, совпадающие с двумя его сторонами 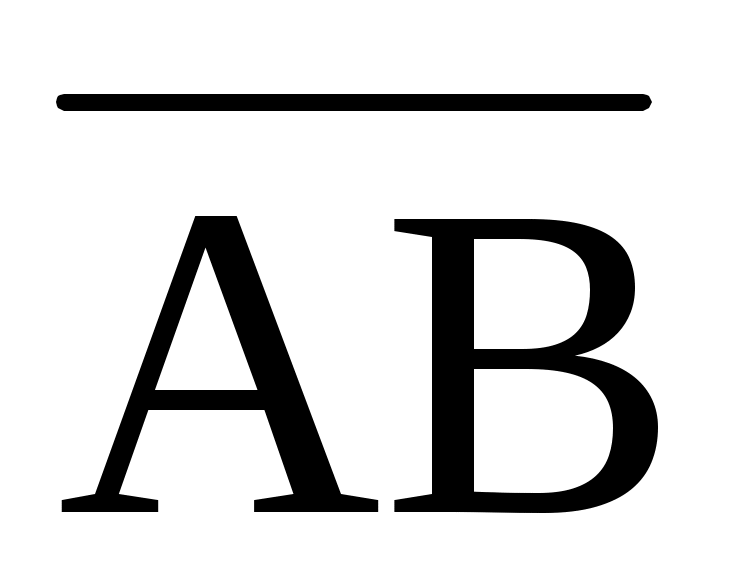 (2; 2; 5), (2; 2; 5), 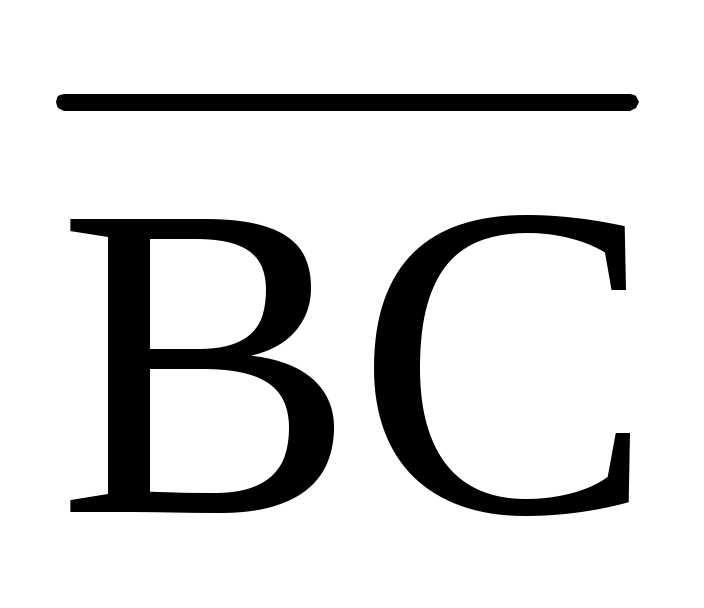 (-1; 3; 4), найти остальные вершины и (-1; 3; 4), найти остальные вершины и  . .
1.9. Векторы 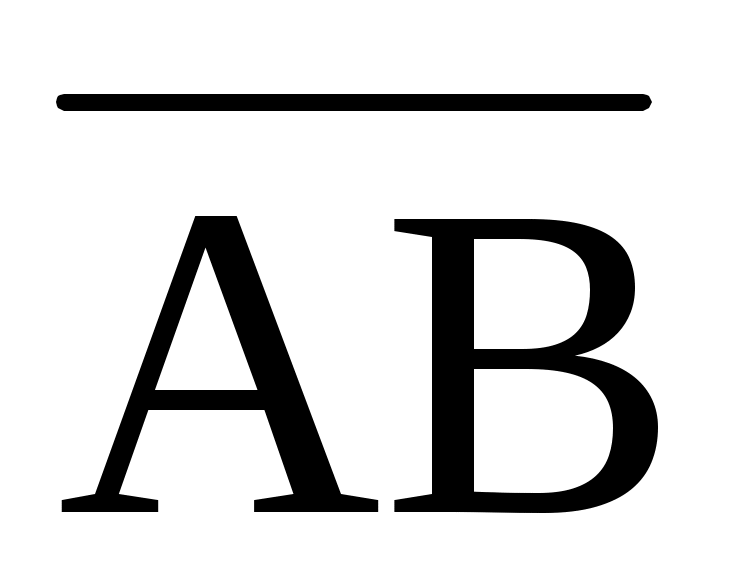 (4; -2; 2) и (4; -2; 2) и 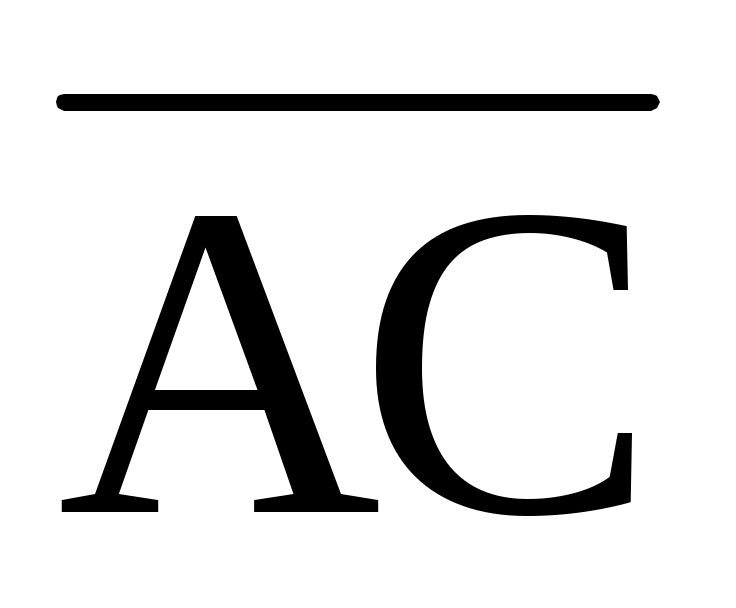 (-2; 6; 0) совпадают со сторонами треугольника АВС. Определить координаты векторов, совпадающих с его медианами (-2; 6; 0) совпадают со сторонами треугольника АВС. Определить координаты векторов, совпадающих с его медианами 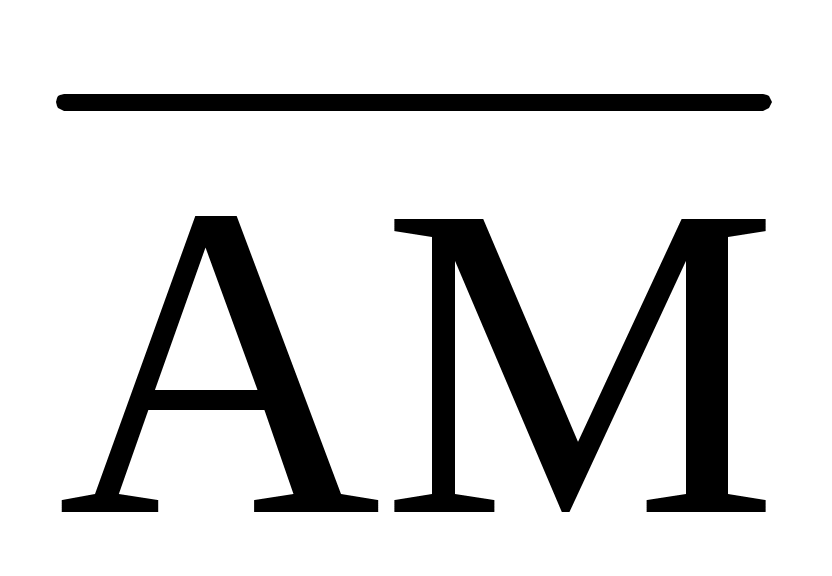 , ,  , ,  . .
1.10. Даны точки А(-1; 5; -10), В(5; -7; 8), С(2; 2; -7), D(5; -4; 2). Проверить, что векторы 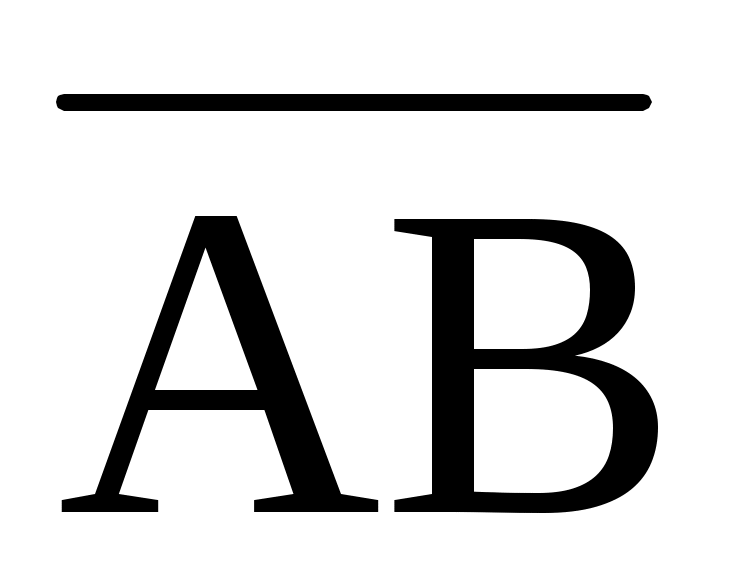 и и  коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны; записать соотношение между этими векторами. коллинеарны, установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны; записать соотношение между этими векторами.
1.11. Проверить, что четыре точки А(3; -1; 2), В(1; 2; -1), С(-1; 1; -3),
D(3; -5; 3) служат вершинами трапеции.
1.12. Доказать, что четырёхугольник ABCD – ромб, если А(-1; 0; 3), В(2; 2; 4), С(3; 5; 2), D(0; 3; 1).
1.13. Доказать, что четырёхугольник ABCD – параллелограмм, если А(1; 2; -3), В(2; -3; 4), С(1; 5; -4), D(5; 3; -2).
1.14. Даны вершины треугольника АВС: А(3; 5; -1), В(1; 1; 2), С(-2; 7; -1). Выяснить, является ли треугольник равносторонним, равнобедренным или разносторонним.
1.15. Треугольник АВС – равнобедренный с основанием АВ. Найти координаты вершины С, если известно: А(1; 2; -2), В(-1; 4; 0), СОх.
1.16. Даны векторы 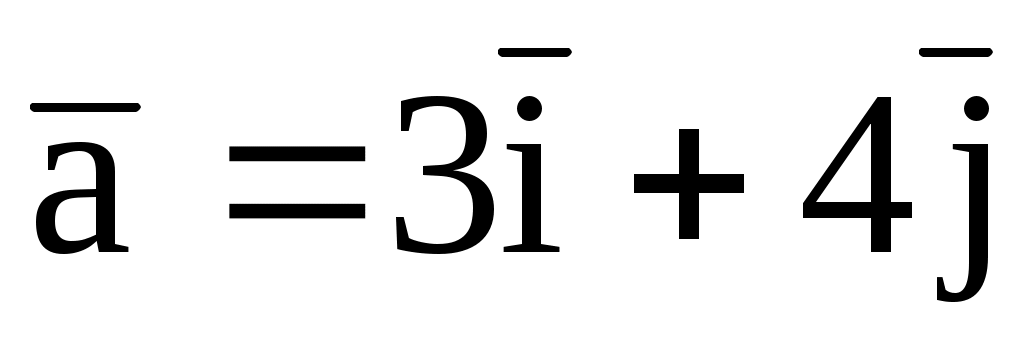 и и 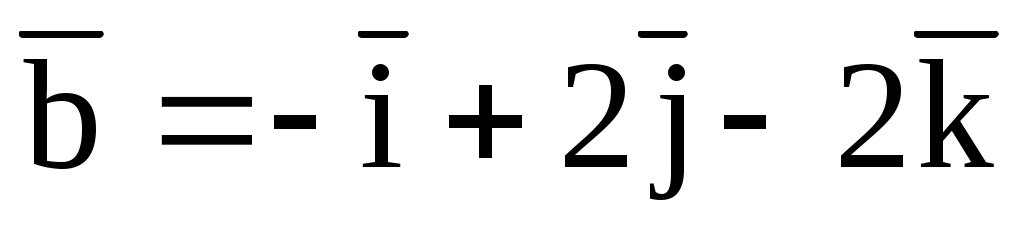 , приложенные к общей точке. Найти орт биссектрисы угла между , приложенные к общей точке. Найти орт биссектрисы угла между  и и  . .
1.17. Два вектора  (1; 2; 2) и (1; 2; 2) и  (3; 0; 4) приложены к одной точке. Определить координаты вектора (3; 0; 4) приложены к одной точке. Определить координаты вектора 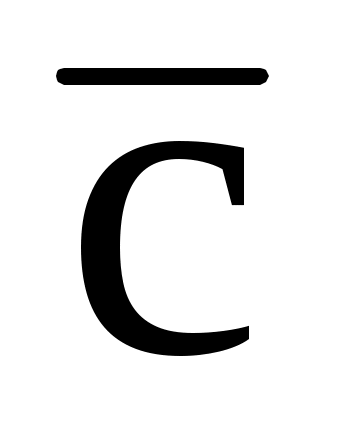 , направленного по биссектрисе угла между векторами , направленного по биссектрисе угла между векторами  и и  , если , если 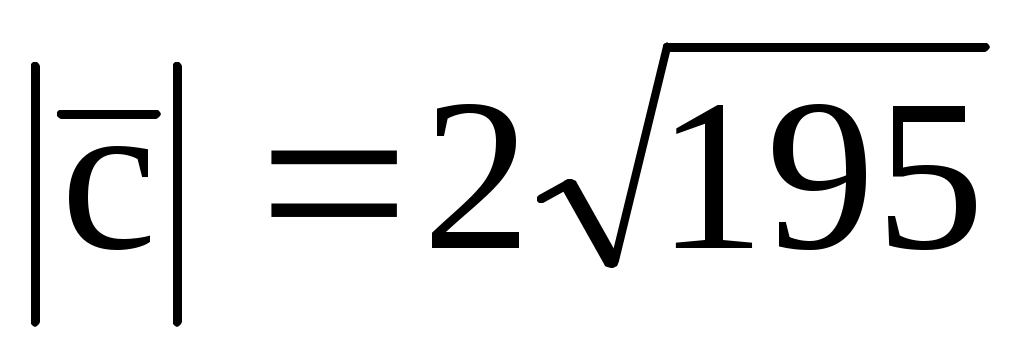 . .
1.18. Два вектора  (2; -3; 6) и (2; -3; 6) и  (-1; 2; -2) приложены к одной точке. Определить координаты вектора (-1; 2; -2) приложены к одной точке. Определить координаты вектора 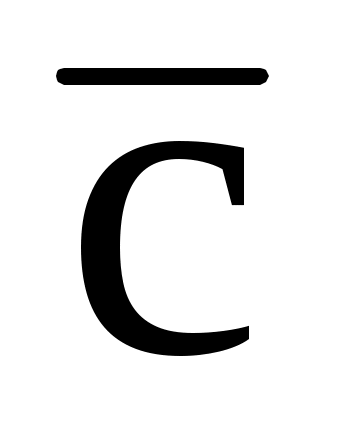 , направленного по биссектрисе угла между векторами , направленного по биссектрисе угла между векторами  и и  , при условии, что , при условии, что 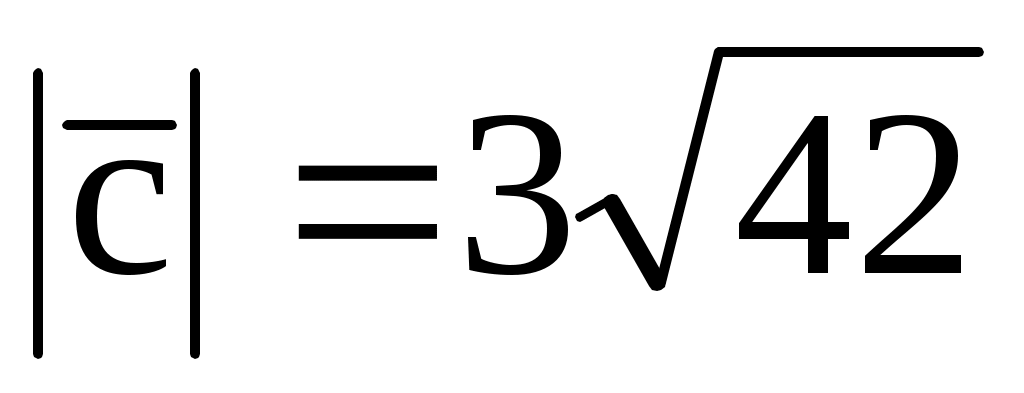 . .
1.19. Даны точки А(1; 2; -3), В(2; -3; 4), С(1; 5; -4), D(5; 3; -2). Доказать, что середины звеньев замкнутой ломанной ABCD являются вершинами параллелограмма.
1.20. В треугольнике АВС известны координаты вершины А(2; -1; 1) и векторы 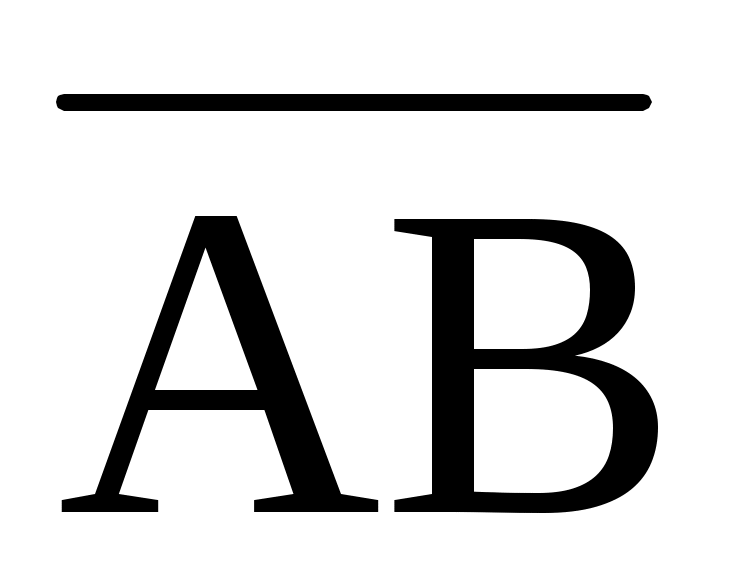 = (-3; 1; 2) и = (-3; 1; 2) и 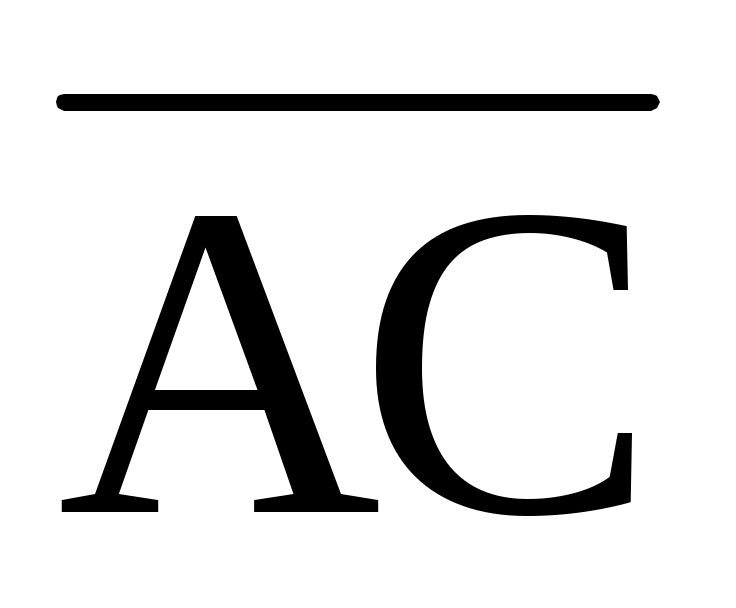 = =  . Найти координаты конца вектора, совпадающего с медианой . Найти координаты конца вектора, совпадающего с медианой 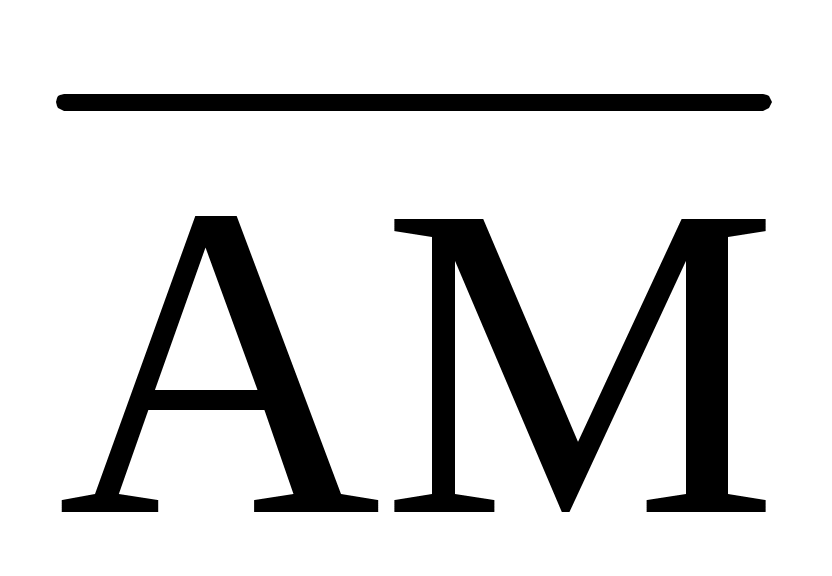 . .
1.21. Вектор  составляет с координатными осями Ox и Oy углы составляет с координатными осями Ox и Oy углы 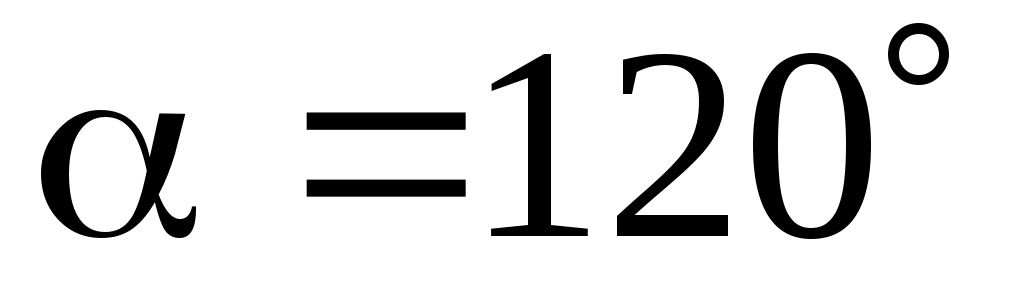 , , 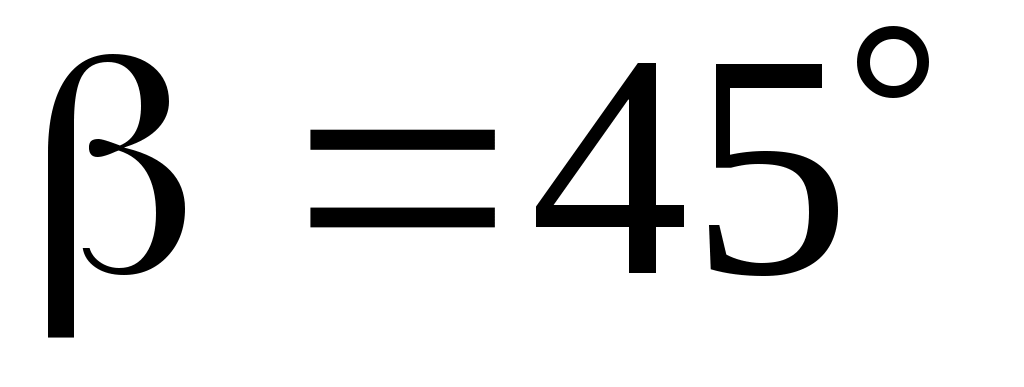 , а с осью Oz – тупой угол. Вычислить его координаты при условии, что , а с осью Oz – тупой угол. Вычислить его координаты при условии, что  = 8. = 8.
1.22. Вектор 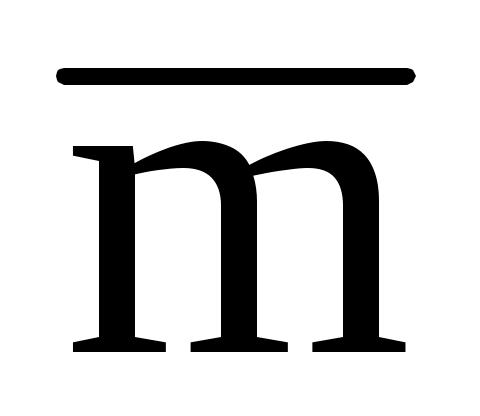 составляет с координатными осями Ox и Oz углы составляет с координатными осями Ox и Oz углы 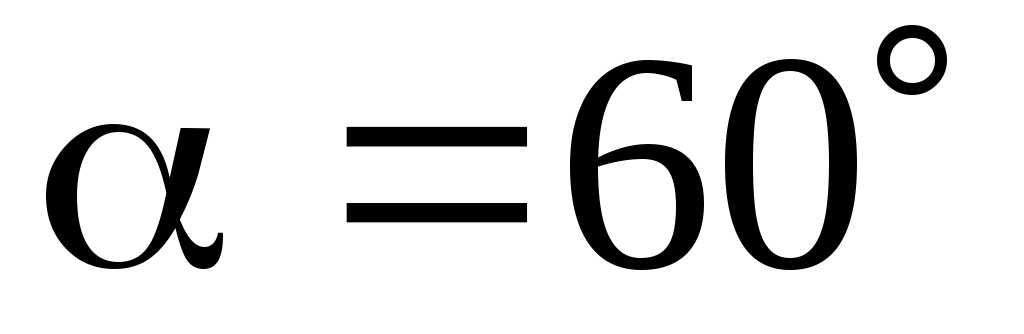 , , 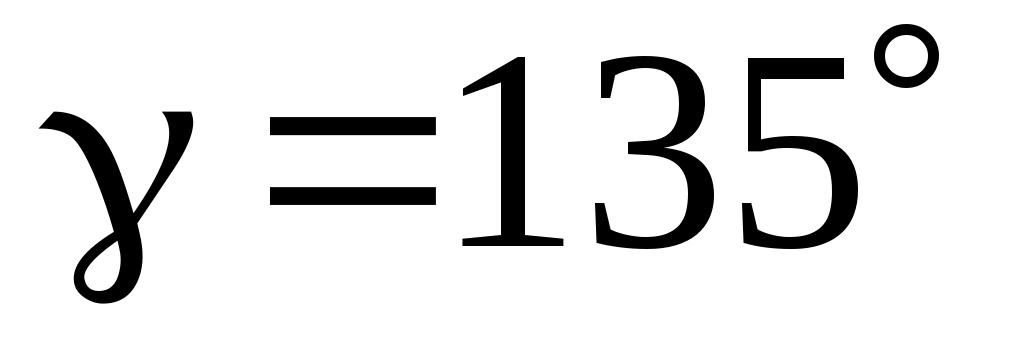 , а с осью Oy – тупой угол. Найти его координаты при условии, что , а с осью Oy – тупой угол. Найти его координаты при условии, что 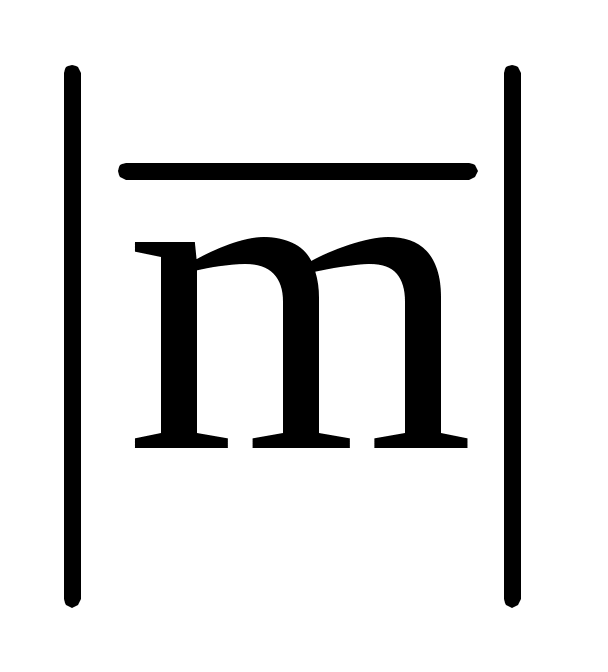 = 12. = 12.
1.23. Вектор 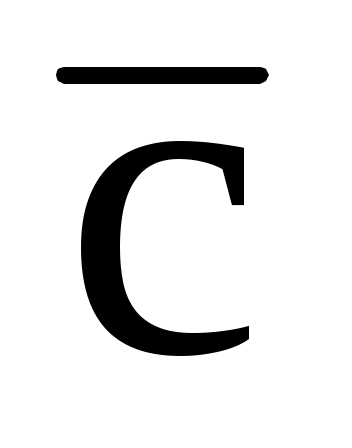 составляет с координатными осями Oy и Oz углы составляет с координатными осями Oy и Oz углы 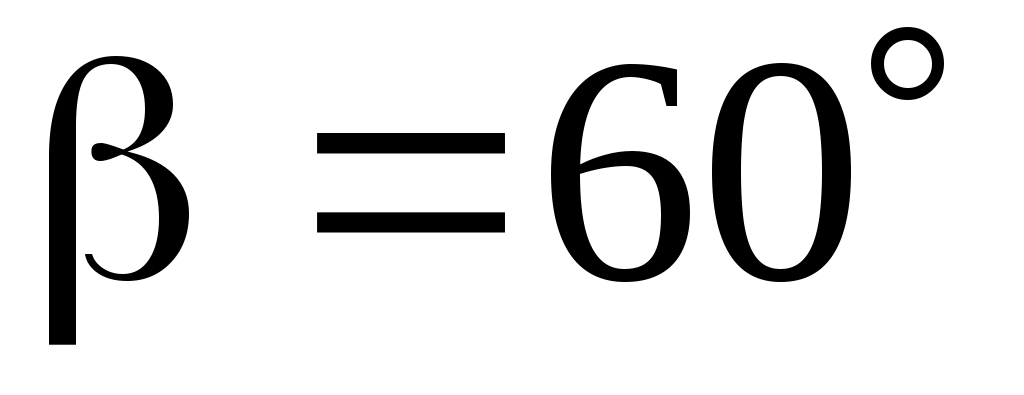 , , 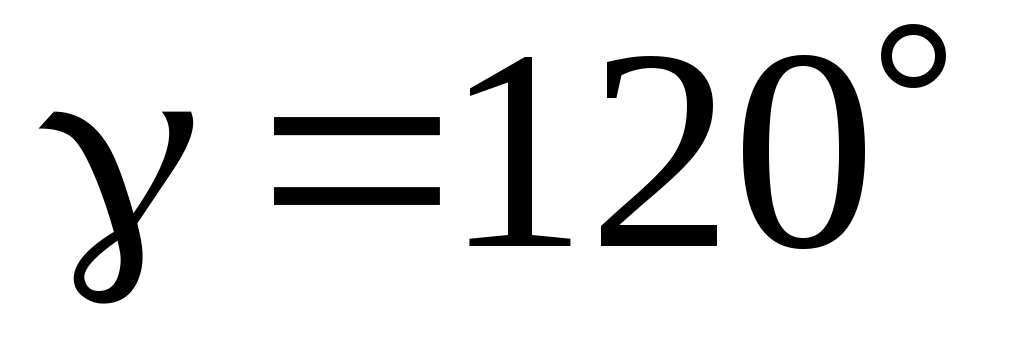 , а с осью Ox – тупой угол. Найти его координаты при условии, что , а с осью Ox – тупой угол. Найти его координаты при условии, что  = = 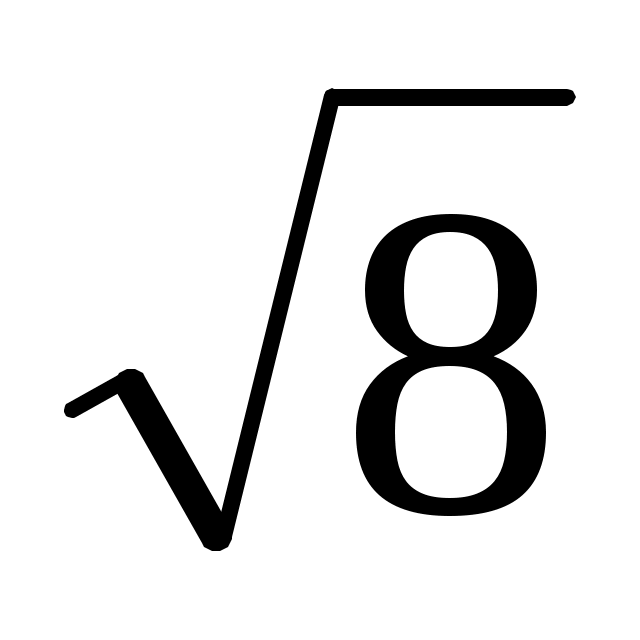 . .
1.24. Найти координаты вектора  , образующего равные острые углы с осями координат, при условии, что , образующего равные острые углы с осями координат, при условии, что  = = 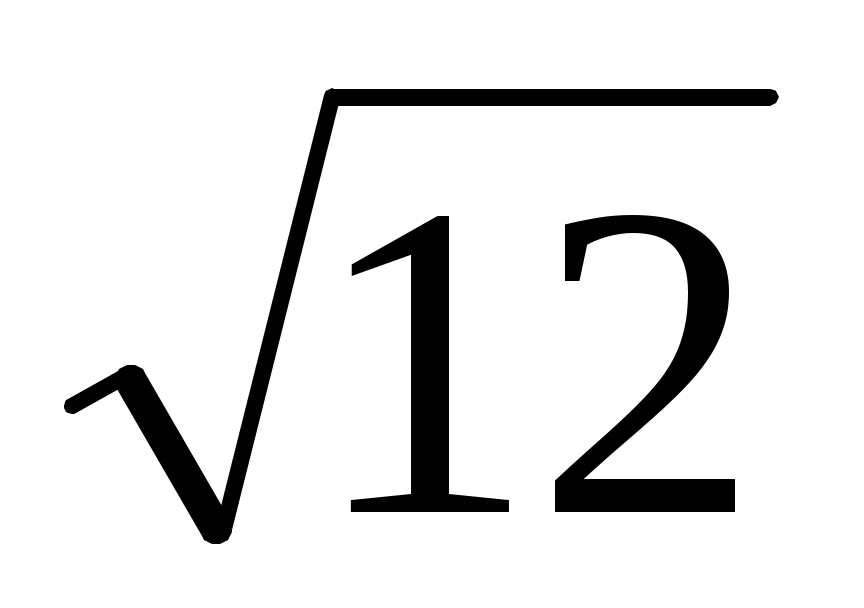 . .
1.25. Найти координаты единичного вектора  , образующего с осями координат равные тупые углы. , образующего с осями координат равные тупые углы.
1.26. Показать, что векторы  , ,  и и 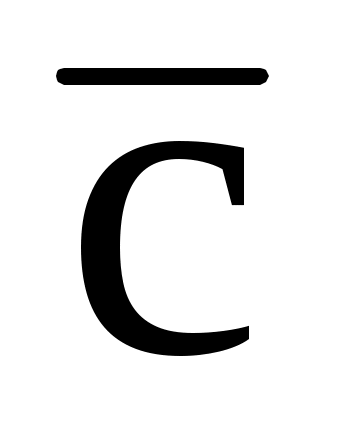 некомпланарны и разложить вектор некомпланарны и разложить вектор 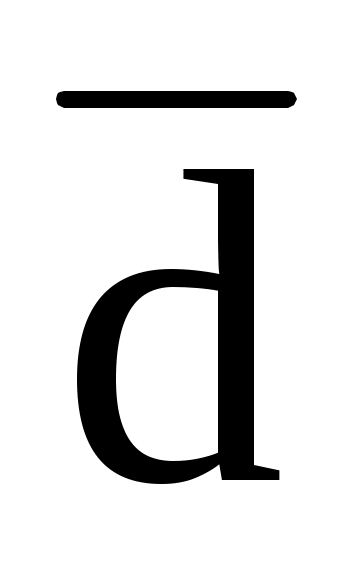 по векторам по векторам  , ,  , , 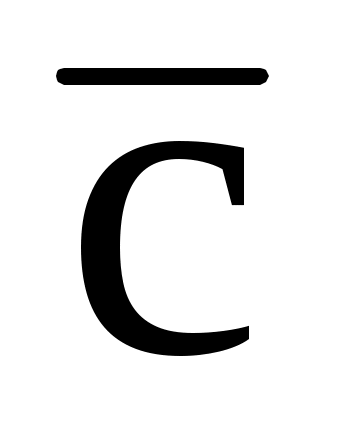 : :
а)  (3; -1; 2), (3; -1; 2),  (-1; 1; -2), (-1; 1; -2), 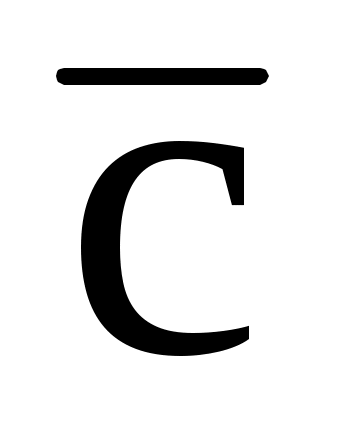 (2; 1; -3), (2; 1; -3), 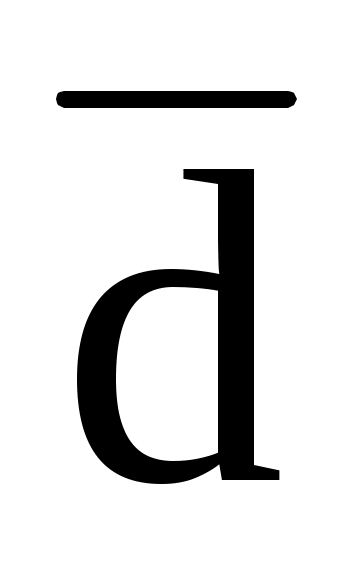 (11; -6; 5); (11; -6; 5);
б)  (2; 3; 1), (2; 3; 1),  (-1; 2; -2), (-1; 2; -2), 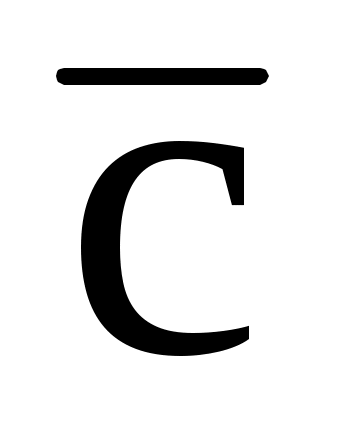 (1; 2; 1), (1; 2; 1), 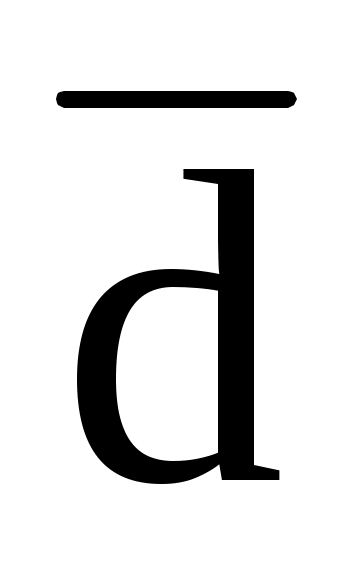 (2; -2; 1); (2; -2; 1);
в)  (1; -1; 1), (1; -1; 1),  (3; -1; 2), (3; -1; 2), 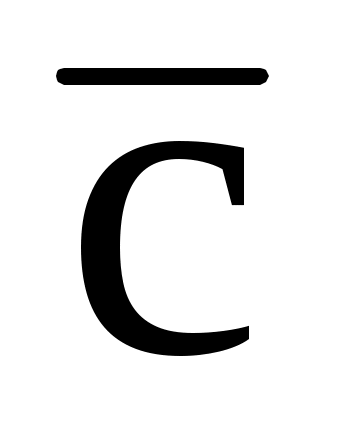 (-2; 2; 1), (-2; 2; 1), 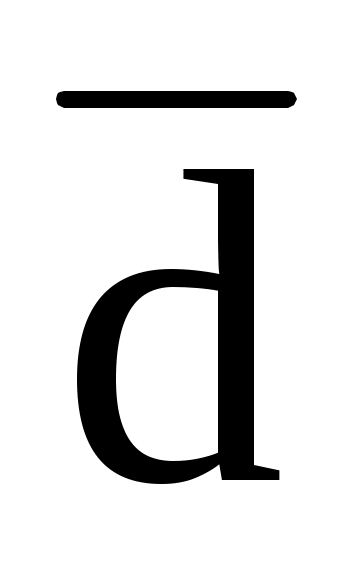 (-5; -1; -5). (-5; -1; -5).
1.27. На плоскости даны четыре точки: A(1; -2), B(2;1), C(3; 2) и D(-2; 3). Найти разложение вектора  + +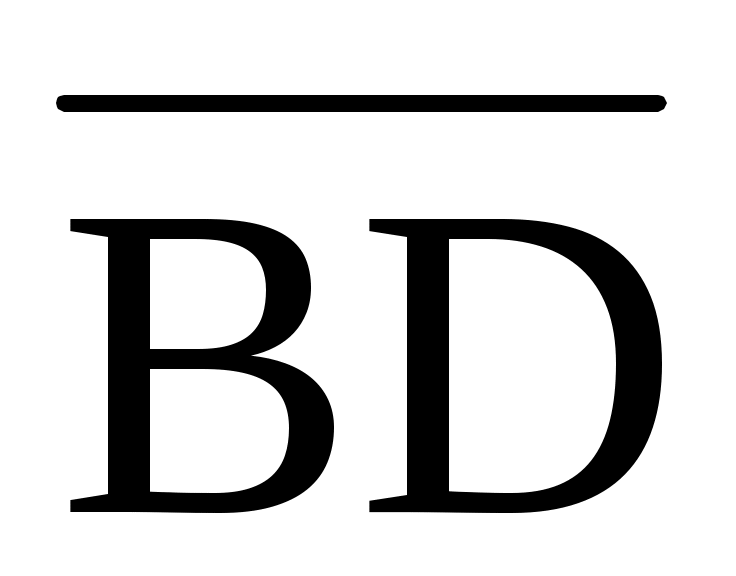 + + , приняв в качестве базиса векторы , приняв в качестве базиса векторы 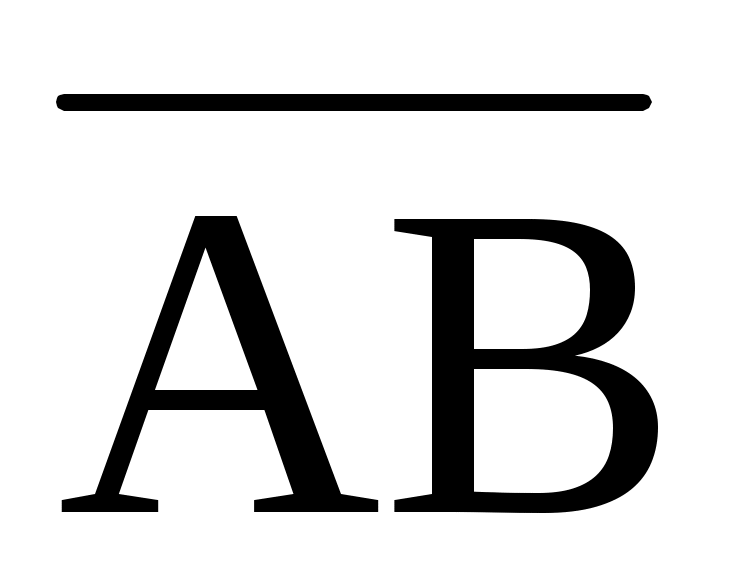 и и 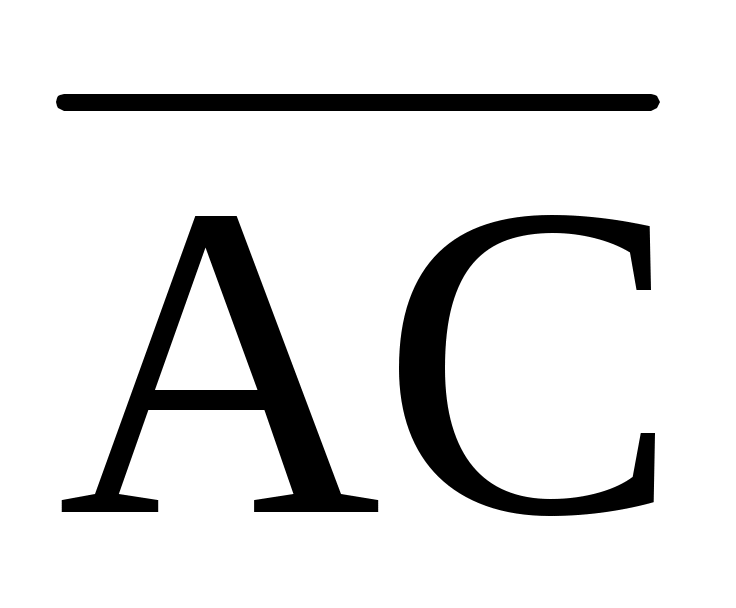 . .
1.28. Показать, что векторы  , ,  , , 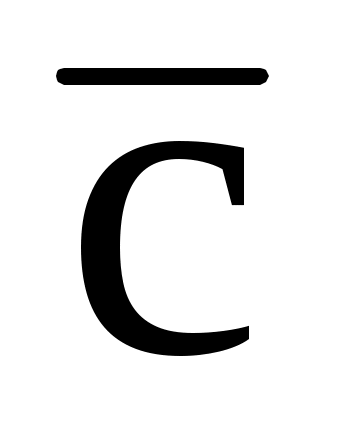 компланарны, и разложить вектор компланарны, и разложить вектор 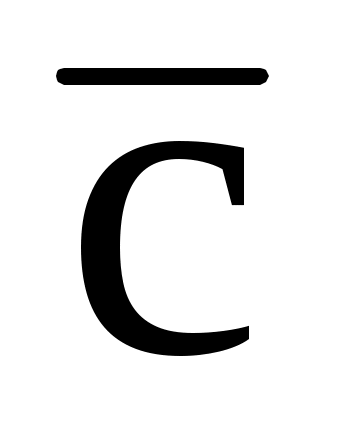 по векторам по векторам  , ,  : :
а)  (-1; 3; 2), (-1; 3; 2),  (2; -3; -4), (2; -3; -4), 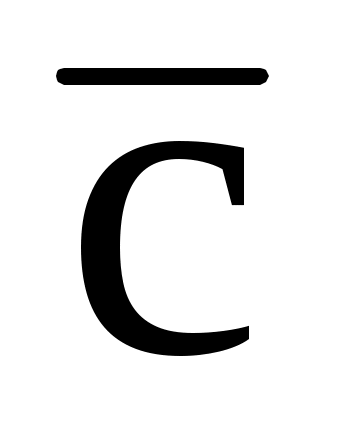 (-3; 12; 6); (-3; 12; 6);
б)  (3; -1; 0), (3; -1; 0),  (0; 2; -1), (0; 2; -1), 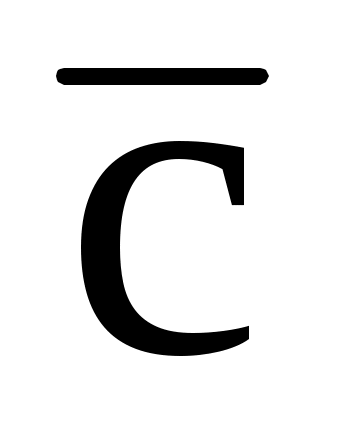 (-9; 7; -2). (-9; 7; -2).
Задание 2
Даны координаты вершин треугольника АВС. Найти: а) углы треугольника; б) 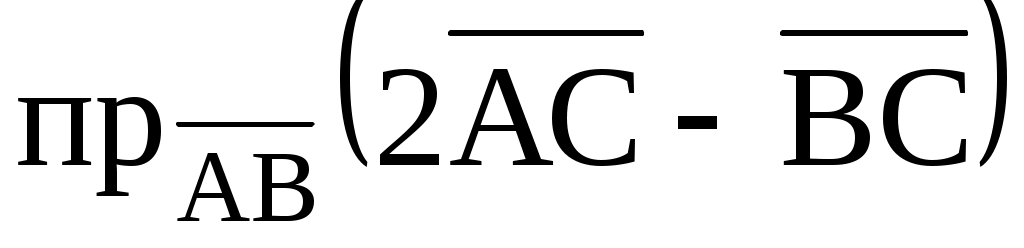 , если , если
№
|
А
|
В
|
С
|
2.1
|
(0; -2; -1)
|
(2; 2; -2)
|
(-4; 2; 1)
|
2.2
|
(1; 2; 0)
|
(5; 4; -4)
|
(3; 6; 4)
|
2.3
|
(-1; -2; 0)
|
(1; 2; 4)
|
(-5; -4; 4)
|
2.4
|
(1; 0; -2)
|
(5; 2; 2)
|
(-1; -4; 2)
|
2.5
|
(-1; 1; 0)
|
(3; -1; 4)
|
(-3; 5; 4)
|
2.6
|
(0; 2; 1)
|
(-4; 4; 5)
|
(2; -2; 5)
|
2.7
|
(-1; 0; -2)
|
(1; 4; -6)
|
(3; 1; 2)
|
2.8
|
(1; -2; 0)
|
(3; -6; 4)
|
(5; 2; 2)
|
2.9
|
(1; 1; 0)
|
(5; 3; -4)
|
(5; -3; 2)
|
2.10
|
(-1; 2; 0)
|
(3; 6; 2)
|
(-3; 6; -4)
|
2.11
|
(0; 1; -1)
|
(-2; 5; 3)
|
(4; -3; -3)
|
2.12
|
(-2; 1; 0)
|
(0; 5; -4)
|
(-6; 5; 2)
|
2.13
|
(0; -1; -2)
|
(-4; 3; 0)
|
(2; 3; -6)
|
2.14
|
(2; -1; 0)
|
(0; 3; 4)
|
(6; 3; -2)
|
2.15
|
(1; -1; -1)
|
(3; 3; 3)
|
(-3; 3; -3)
|
2.16
|
(1; 0; 2)
|
(3; 1; 0)
|
(2; 2; 4)
|
2.17
|
(0; -1; 2)
|
(-2; -2; 4)
|
(1; 1; 4)
|
2.18
|
(0; 1; -1)
|
(2; 2; 0)
|
(-1; -1; 0)
|
2.19
|
(-1; 0; 2)
|
(1; -1; 4)
|
(-2; 2; 4)
|
2.20
|
(0; 1; 2)
|
(-2; 2; 4)
|
(1; -1; 4)
|
2.21
|
(-2; 0; -1)
|
(-1; 2; -3)
|
(0; 1; 1)
|
2.22
|
(0; 2; -1)
|
(1; 0; 1)
|
(2; 4; 0)
|
2.23
|
(1; 0; -1)
|
(3; 1; -3)
|
(3; -2; 0)
|
2.24
|
(1; 2; 0)
|
(0; 4; -2)
|
(3; 4; 1)
|
2.25
|
(-1; 0; 2)
|
(1; 2; 3)
|
(1; -1; 0)
|
2.26
|
(-2; 0; 1)
|
(0; 1; 3)
|
(0; -2; 0)
|
2.27
|
(2; 0; -1)
|
(3; 2; 1)
|
(0; 2; -2)
|
2.28
|
(2; 1; 0)
|
(1; 3; 2)
|
(4; 0; 2)
|
2.29
|
(-2; -1; 0)
|
(-3; 1; 2)
|
(0; 1; -1)
|
2.30
|
(0; -2; 1)
|
(-2; 0; 2)
|
(1; 0; -1)
|
|
 Скачать 1.31 Mb.
Скачать 1.31 Mb.