Векторная алгебра 1. Векторная алгебра и аналитическая геометрия.ТРЗ. Типовое расчётное задание

• Название: Типовое расчётное задание
• Анкор: Векторная алгебра 1
• Дата: 03.05.2023
• Размер: 1.31 Mb.
• Имя файла: Векторная алгебра и аналитическая геометрия.ТРЗ.doc
• Тип: Документы; #1106340
• страница: 5 из 6

Задание 11

11.1. Составить уравнение окружности, для которой концами одного диаметра являются точка К(-3; 2) и точка пересечения прямых и .

11.2. Составить уравнение окружности, проходящей через три точки:
А(4; 1), В(-2; 3), С(2; -5).

11.3. Составить уравнение окружности с центром в точке М(1; -3), касающейся прямой .

11.4. Найти кратчайшее расстояние от точки А(-6; 6) до окружности .

11.5. Найти расстояние от центра окружности до прямой .

11.6. Найти расстояние от центра окружности до прямой .

11.7. Составить уравнение линии центров окружностей и .

11.8. Составить уравнение прямой, проходящей через точку С(3; -4) и через центр окружности .

11.9. Составить уравнение диаметра окружности , параллельного прямой .

11.10. Составить уравнение диаметра окружности , перпендикулярного прямой .

11.11. Составить уравнение диаметра окружности , проходящего через точку пересечения прямых и .

11.12. Составить уравнение диаметра окружности , параллельного биссектрисе II – IV координатных углов.

11.13. Составить уравнение касательных к окружности в точках её пересечения с осью Oy.

11.14. Составить уравнение касательных к окружности в точках её пересечения с осью Ox.

11.15. Составить уравнения касательных к окружности в точках её пересечения с биссектрисой I – III координатных углов.

11.16. Найти центр и полуоси эллипса . Сделать чертёж.

11.17. Для эллипса найти его межфокусное расстояние.

11.18. Составить уравнение прямой, проходящей через точку С(-3; 4) и через центр эллипса .

11.19. Найти эксцентриситет эллипса .

11.20. Фокусы эллипса совпадают с фокусами гиперболы . Составить каноническое уравнение эллипса, если его эксцентриситет .

11.21. Через фокус эллипса проведена хорда, перпендикулярная к его большой оси. Найти длину хорды.

11.22. Для гиперболы найти полуоси и координаты центра. Сделать чертёж.

11.23. Составить уравнение прямой, проходящей через точку М(-1; 3) и через центр гиперболы .

11.24. Найти координаты фокусов гиперболы .

11.25. Найти эксцентриситет гиперболы .

11.26. Составить уравнения асимптот гиперболы .

11.27. Через фокус гиперболы проведена хорда, перпендикулярная к её действительной оси. Найти длину хорды.

11.28. Составить уравнение прямой, проходящей через фокус параболы и через точку К(2; 5).

11.29. Составить уравнение прямой, проходящей через вершину параболы и через точку Р(2; 4).

11.30. Через фокус параболы проведена хорда, параллельная оси Ox. Найти её длину.
Задание 12

Даны координаты вершин пирамиды А₁, А₂, А₃, А₄; а) составить уравнение плоскости А₁А₂А₃; б) составить уравнения рёбер А₁А₂, А₁А₄ и высоты, опущенной из вершины А₄ на грань А₁А₂А₃; в) найти угол между рёбрами А₁А₂ и А₁А₄; г) найти угол между ребром А₁А₄ и гранью А₁А₂А₃.

№	А1	А2	А3	А4
12.1	(10; 6; 6)	(-2; 8; 2)	(6; 8; 9)	(7; 10; 3)
12.2	(1; 8; 2)	(5; 2; 6)	(5; 7; 4)	(4; 10; 9)
12.3	(6; 6; 5)	(4; 9; 5)	(4; 6; 11)	(6; 9; 3)
12.4	(7; 2; 2)	(5; 7; 7)	(5; 3; 1)	(2; 3; 7)
12.5	(6; 6; 4)	(10; 5; 5)	(5; 6; 8)	(8; 10; 7)
12.6	(7; 7; 2)	(6; 5; 8)	(3; 5; 8)	(8; 4; 10)
12.7	(-3; 1; 4)	(1; 6; 1)	(1; 1; 6)	(0; 4; -1)
12.8	(-3; 3; 9)	(-6; 9; 1)	(-1; 7; 3)	(-8; 5; 8)
12.9	(-3; 5; 4)	(-5; 8; 3)	(-1; 9; 9)	(-6; 4; 8)
12.10	(-2; 4; 3)	(-7; 6; 3)	(-4; 9; 3)	(-3; 6; 7)
12.11	(-9; 5; 5)	(7; 3; 1)	(-5; 7; 8)	(-6; 9; 2)
12.12	(0; 7; 1)	(-4; 1; 5)	(-4; 6; 2)	(-3; 9; 8)
12.13	(-5; 5; 4)	(-3; 8; 4)	(-3; 5; 10)	(-5; 8; 2)
12.14	(-6; 1; 1)	(-4; 6; 6)	(-4; 2; 0)	(-1; 2; 6)
12.15	(-7; 5; 3)	(-9; 4; 4)	(-4; 5; 7)	(-7; 9; 6)
12.16	(-6; 6; 2)	(-5; 4; 7)	(-2; 4; 7)	(-7; 3; 0)
12.17	(3; 1; 4)	(-1; 6; 1)	(-1; 1; 6)	(0; 4; -1)
12.18	(3; 3; 9)	(6; 9; 1)	(1; 7; 3)	(8; 5; 8)
12.19	(3; 5; 4)	(5; 8; 3)	(1; 9; 9)	(6; 4; 8)
12.20	(2; 4; 3)	(7; 6; 3)	(4; 9; 3)	(3; 6; 9)
12.21	(9; 5; 5)	(-3; 7; 1)	(5; 7; 8)	(6; 9; 2)
12.22	(0; 7; 1)	(4; 1; 5)	(4; 6; 3)	(3; 9; 8)
12.23	(5; 5; 4)	(3; 8; 4)	(3; 5; 10)	(5; 8; 2)
12.24	(6; 1; 1)	(4; 6; 6)	(4; 2; 0)	(1; 2; 6)
12.25	(7; 5; 3)	(9; 4; 4)	(4; 5; 7)	(7; 9; 6)
12.26	(6; 6; 2)	(5; 4; 7)	(2; 4; 7)	(7; 3; 0)
12.27	(4; 2; 5)	(0; 7; 2)	(0; 2; 7)	(1; 5; 0)
12.28	(4; 4; 10)	(7; 10; 2)	(2; 8; 4)	(9; 6; 9)
12.29	(4; 6; 5)	(6; 9; 4)	(2; 10; 10)	(7; 5; 9)
12.30	(3; 5; 4)	(8; 7; 4)	(5; 10; 4)	(4; 7; 8)

Задание 13

13.1. Составить уравнение плоскости, проходящей через точку М перпендикулярно плоскостям ₁ и ₂, если:

а) М(1; -1; 2); ₁: ; ₂: .

б) М(2; 1; -3); ₁: ; ₂: .

в) М(-1; 2; 2); ₁: ; ₂: .

13.2. Составить уравнение плоскости, проходящей через точки М и N перпендикулярно плоскости , если:

а) М(3; 3; 1); N(-1; 2; 2); : .

б) М(-2; 1; 2); N(3; 1; 3); : .

в) М(1; 2; -1); N(2; 0; 4); : .

13.3. Составить уравнение плоскости, проходящей через точку М параллельно прямым l₁ и l₂, если:

а) М(1; 2; -3); l₁: 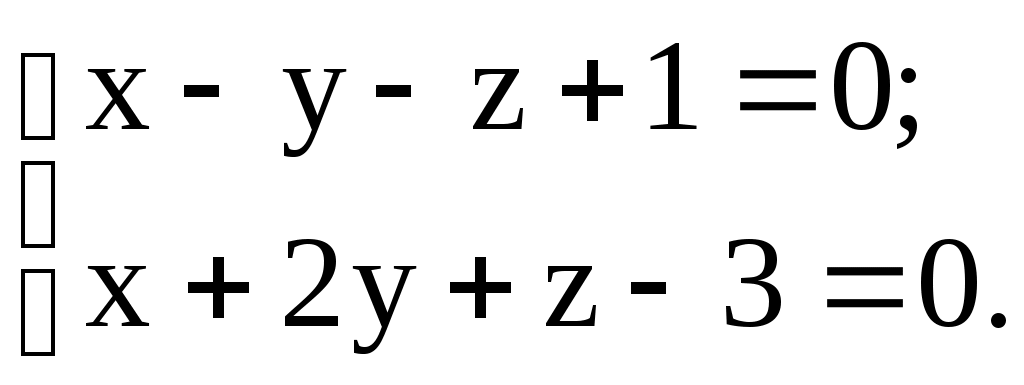; l₂: .

б) М(-2; 1; 2); l₁: ; l₂: ; ; .

в) М(3; 0; 1); l₁: ; l₂:

13.4. Составить уравнение плоскости, проходящей через точку М и через прямую l, если:

а) М(1; -1; 1); l: .

б) М(3; 1; -2); l: ; ; .

в) М(-2; 2; 3); l: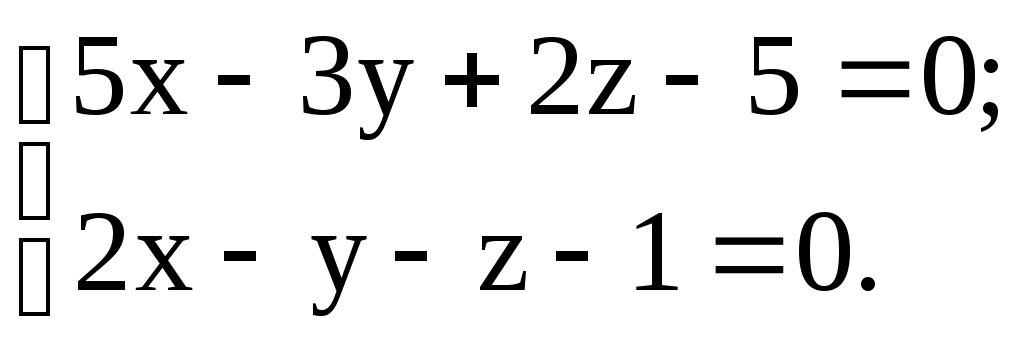

13.5. Составить уравнение плоскости, проходящей через прямую l перпендикулярно плоскости , если:

а) l: ; : .

б) l: ; ; ; : .

в) l: : .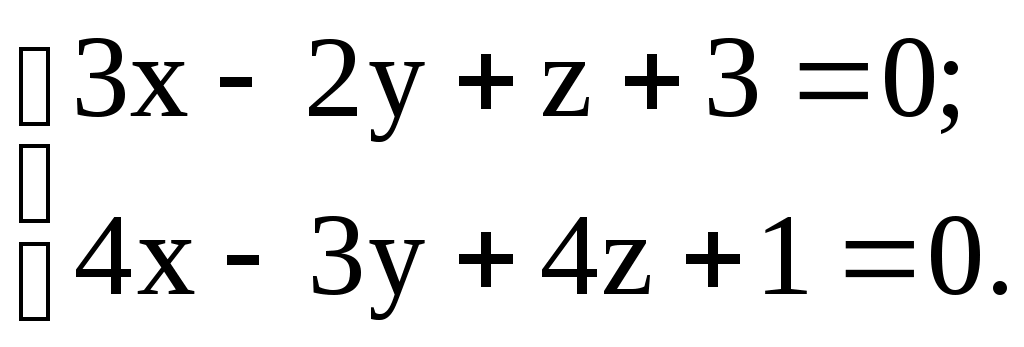

13.6. Составить уравнение плоскости, проходящей через две параллельные прямые l₁ и l₂, если:

а) l₁: ; l₂: .

б) l₁: ; l₂: ; ; .

в) l₁: ; l₂: ; ; .

12.7. Составить параметрические уравнения прямой, проходящей через точки пересечения плоскости  с прямыми l₁ и l₂, если:

а) : ; l₁: ; l₂: .

б) : ; l₁: ; l₂: .

в) : ; l₁: ; l₂: .

12.8. Выяснить возможное расположение прямых l₁ и l₂ в пространстве, если:

а) l₁: 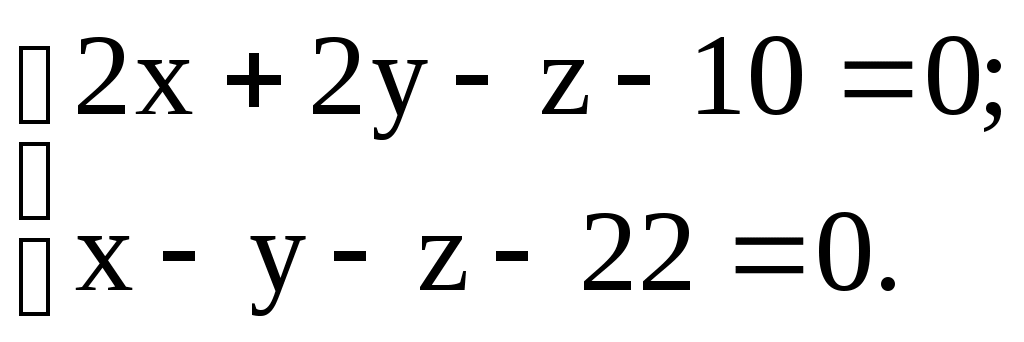; ; ; l₂: .

б) l₁: ; ; ;

 l₂: ; ; .

в) l₁: 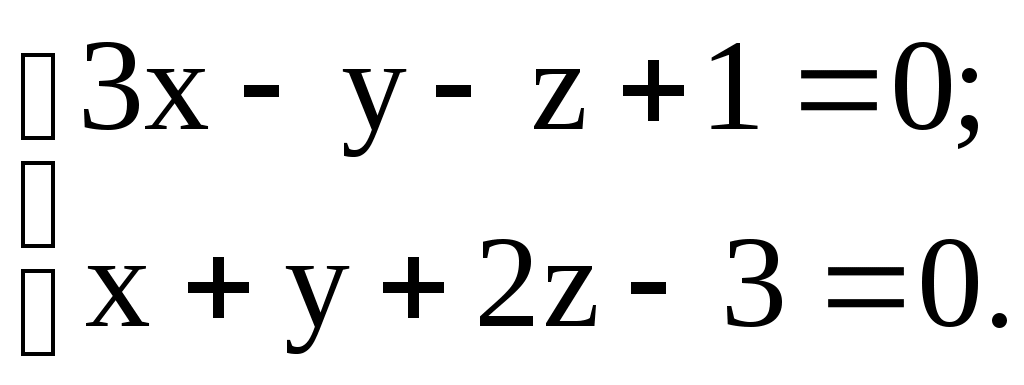; l₂: ; ; .

12.9. Составить уравнение перпендикуляра, опущенного из точки А на прямую l, если:

а) А(2; 5; -5); l: .

б) А(3; 1; -4); l: .

в) А(3; -1; 5); l: ; ; .

12.10. Составить уравнение прямой, которая проходит через точку М и пересекает прямые l₁ и l₂, если:

а) М(2; -9; -1); l₁: ; l₂: .

б) М(0; 9; -5); l₁: ; ; ;

l₂: .

в) М(-5; -1; 10); l₁: ; l₂: .