Учебный курс для студентов очной и заочной форм обучения
 Скачать 5.65 Mb.
|
|
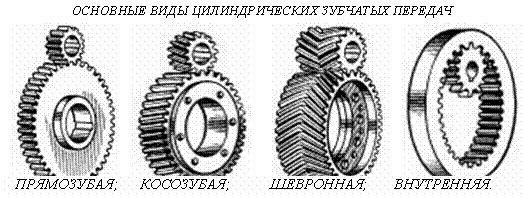
Раздел 5. Зубчатые передачи. Преимущественное распространение получили передачи с зубьями эвольвентного профиля, которые изготавливаются массовым методом обкатки на зубофрезерных или зубодолбежных станках. Достоинство эвольвентного зацепления состоит в том, что оно мало чувствительно к колебанию межцентрового расстояния. Другие виды зацепления применяются пока ограниченно. Так, циклоидальное зацепление, при котором возможна работа шестерен с очень малым числом зубьев (2-3), не может быть, к сожалению, изготовлено современным высокопроизводительным методом обкатки, поэтому шестерни этого зацепления трудоемки в изготовлении и дороги; новое пространственное зацепление Новикова пока еще не получило массового распространения, вследствие большой чувствительности к колебаниям межцентро вого расстояния.
Прямозубые колёса (около 70%) применяют при невысоких и средних скоростях, когда динамические нагрузки от неточности изготовления невелики, в планетарных, открытых передачах, а также при необходимости осевого перемещения колёс. Косозубые колёса (более 30%) имеют большую плавность хода и применяются для ответственных механизмов при средних и высоких скоростях. Шевронные колёса имеют достоинства косозубых колёс плюс уравновешенные осевые силы и используются в высоконагруженных передачах. Колёса внутреннего зацепления вращаются в одинаковых направлениях и применяются обычно в планетарных передачах. Выбор параметров цилиндрических зубчатых передач обусловлен конструктивными и технологическими условиями. Передаточное отношение U определяется соотношением угловых скоростей (ω) или частот вращения (n) ведомого и ведущего колёс U = ω1 / ω2 = n1 / n2. Здесь и далее индексы 1 и 2 расставлены в порядке передачи механической энергии 1- ведущее (шестерня), 2- ведомое (колесо). Учитывая, что в зацепление входят колёса с одинаковым модулем (ГОСТ 9563-60), можно задавшись числом зубьев шестерни Z1найти число зубьев колеса Z2 = U * Z1. Передаточное число U ограничено габаритами зубчатой передачи. Его рекомендуется принимать в диапазоне от 2 до 6. Нормальный ряд значений U стандартизирован в ГОСТ 2185-66. Ширина колеса задаётся обычно коэффициентом ширины Ya= b / Aw , где b – ширина венца; Aw – межосевое расстояние (ГОСТ 2185-66). Критерии расчёта эвольвентных зубьев Поскольку колёса в зацеплении взаимодействуют своими зубьями, то весьма часто в эксплуатации наблюдаются различные повреждения их рабочих поверхностей. Усталостное выкрашивание является наиболее серьёзным и распространённым дефектом поверхности зубьев даже для закрытых хорошо смазываемых и защищённых от загрязнения передач. На рабочих поверхностях появляются небольшие углубления, которые затем превращаются в раковины. Выкрашивание носит усталостный характер и вызвано контактными напряжениями, которые изменяются по отнулевому пульсирующему циклу. Выкрашивание приводит к повышению контактного давления и нарушению работы передачи. В открытых передачах поверхностные слои истираются раньше, чем в них появляются усталостные трещины, поэтому выкрашивание появляется весьма редко. Для предупреждения выкрашивания необходимо повышать твёрдость материала термообработкой либо повышать степень точности передачи, а также правильно назначать размеры из расчёта на усталость по контактным напряжениям. Абразивный износ является основной причиной выхода из строя передач при плохой смазке. Это, в первую очередь, открытые передачи, а также закрытые, но находящиеся в засорённой среде: в горных, дорожных, строительных, транспортных машинах. У изношенных передач повышаются зазоры в зацеплении и, как следствие, усиливаются шум, вибрация, динамические перегрузки; искажается форма зуба; уменьшаются размеры поперечного сечения, а значит и прочность зуба. Основные меры предупреждения износа – повышение твёрдости поверхности зубьев, защита от загрязнения, применение специальных масел. В расчёте на контактную выносливость абразивный износ учитывается занижением допускаемых контактных напряжений. Заедание происходит в высоконагруженных и высокоскоростных передачах. В месте контакта зубьев возникает повышенная температура, приводящая к молекулярному сцеплению металла с последующим отрывом. Вырванные частицы затем царапают трущиеся поверхности. Обычно заедания происходят вследствие выдавливания масляной плёнки между зубьев при совместном действии высоких давлений и скоростей. Меры предупреждения здесь те же, что и при абразивном износе. Рекомендуется также фланкирование зубьев, правильный выбор сорта масла и его охлаждение. Другой, реже встречающийся, но не менее опасный вид поломок – излом зуба. Такая поломка связана с напряжениями изгиба, также имеющими отнулевой пульсирующий характер. Излом зуба может привести к весьма тяжким последствиям вплоть до разрушения валов и подшипников, а иногда и всего механизма. Для предупреждения излома проводится расчёт зуба по напряжениям изгиба. Такой расчёт для закрытых передач выполняется в качестве проверочного после расчёта на контактные напряжения. Для открытых передач, где высока вероятность случайных перегрузок, этот расчёт выполняется как проектировочный. Усталостное выкрашивание, абразивный износ и заедание обусловлены поверхностной прочностью, а излом – объёмной прочностьюзубьев. Поскольку поверхностные повреждения – главный вид поломок для закрытых передач, то расчёт на контактную выносливость выполняют в качестве проектировочного; расчёт на изгиб – в качестве проверочного. Для открытых передач всё наоборот, т.к. режим работы временный или даже разовый, а перегрузки значительные. Для выполнения расчётов на поверхностную и объёмную прочность рассмотрим силы в зубчатом зацеплении. Основные определения из теории зацепления шестерен 1. Начальными называются воображаемые окружности, которые при зацеплении шестерен катятся без скольжения одна по другой. 2. Делительными называются воображаемые окружности, по которым происходит номинальное деление зубьев. Для них справедливо уравнение: dд = mZ Примечание: Если шестерни не имеют коррекции, то начальные и делитель ные окружности совпадает. 3. Окружностями выступов и впадин называются окружности, ограничивающие вершины и впадины зубьев. 4. Основными называются окружности, по которым развертываются эвольвенты, очерчивающие профили зубьев d0 = dдcosa 5. Шагом t называется расстояние по дуге делитель ной окружности между одноименными профилями соседних зубьев. 6. Основным шагом t0 называется шаг по основной окружности. 7. Модулем называется отношение диаметра делительной окружности к числу зубьев или шага к p. 8. Ритчем р называется число зубьев, приходящееся на один дюйм делительной окружности p = 9. Линией зацепления ЛЗ называется геометрическое место точек контакта зубьев в зацеплении. В эвольвентном зацеплении ЛЗ - прямая, нормальная к профилю зубьев в полюсе зацепления и касательная к основным окружностям. 10. Углом зацепления a называется угол между линией зацепления и перпендикуляром к линии центров. 11. Углом наклона спирали зубьев косозубых шестерен b называется угол между осью зуба и образующей делительного цилиндра или конуса. 12. Коэффициентом перекрытия e называется отношение дуги зацепления к основному шагу. 13. Коэффициентом коррекции x называется отношение величины профильного смещения к модулю. Конструктивные типы шестерен 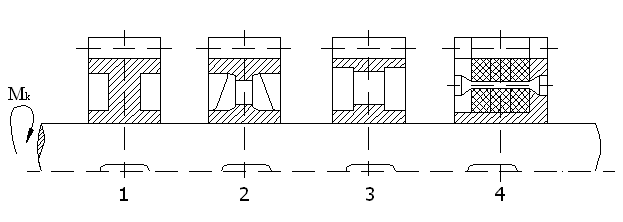 1 - стальные кованые, 2 - литые из серого чугуна, 3 - сварные, 4 - составные из пластмасс. Тип 1 - имеет преимущественное распространение; тип 2 - для малонагруженных передач, а также для открытых передач большого размера; тип 3 - для крупногабаритных шестерен; тип 4 - для бесшумной работы при хорошей сопротивля емости удару. Материал и термообработка шестерен Стальные шестерни изготавливаются из качественных и ле гированных сталей, как правило, с термообработкой. Наибольшее распространение получили: для серийного производства - улучшение; для серийного и массового - цементация и закалка: только для массового производства при наличии зубошлифовальных станков - закалка; для массового производства при наличии соответствующего оборудования - закалка токами высокой частоты. Таблица 1
Расчетные геометрические зависимости а) прямозубые и косозубые цилиндрические шестерни 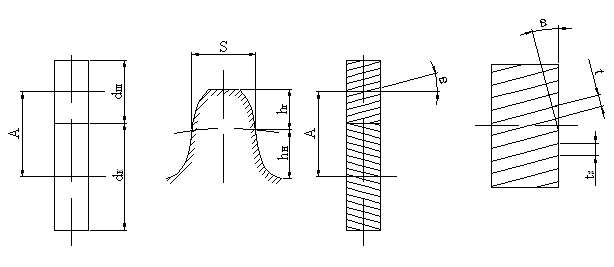 а) передаточное отношение: i = б) делительные диаметры шестерен: dд = mZ - для прямозубых dд = msZ = - для косозубых в) шаг и модуль: m = ; ms = ; ts = ; ms = . г) межцентровое расстояние: - для прямозубых  - для косозубыхд) размеры зуба: hг = f0 m; при f0 = 1, hc = m, hн = 1.25m hн = 1,25 f0m - по дуге; f0 - коэффициент высоты зуба. Здесь: t и m - нормальный шаг и модуль; ts и ms - торцевой шаг и модуль; b - угол спирали зуба. Ряд наиболее распространенных стандартных модулей: ... 1; 1,5; 2; 2,5; 3; 3,5; 4; 4,5; 5; 6; 7; 8; 10; 12 ... Стандартный угол зацепления a - 20°. Для бесшумной и плавной работы косозубых шестерен необходимо перекрытие зубьев: последующий зуб должен входить в зацеп-ление раньше, чем выйдет из зацепления предыдущий. б) прямозубые конические шестерни Все o6paзующие зубьев сходятся в одной точке пересечения осей. Номинальный делительный диаметр, шаг и модуль отсчитываются по большому основанию делительного конуса. 1.Передаточное отношение: i =  2. Делительный и средний диаметры шестерен: dд = m Z; dс = mс Z. 3. Конусное расстояние: 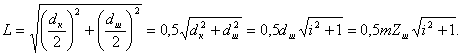 4. Средний диаметр и модуль: . Здесь: mc - средний модуль; L - конусное расстояние - длина образующей делительного конуса; b - ширина зубьев шестерен; g - углы конусности. 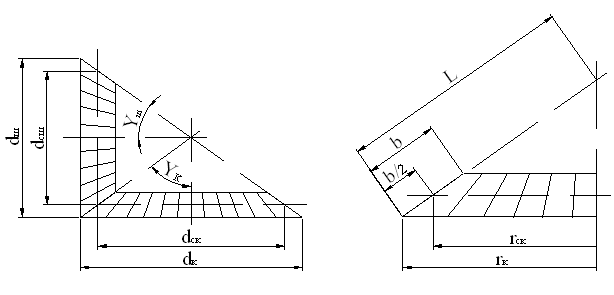 Силы, действующие в зацеплении шестерен 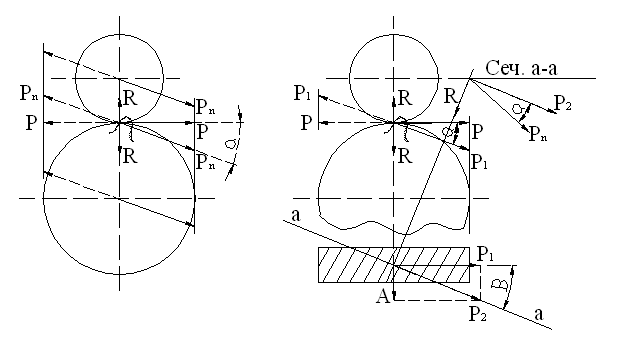 а) прямозубые цилиндрические шестерни Нормальная сила, действующая по линии зацепления, разлагается на две составляющие силы: P = Pn cosa - окружное усилие; R = Pn sina - радиальное усилие; На валы действуют те же силы, что и на зубья шестерен, и, кроме того, еще крутящий момент: б) косозубые цилиндрические шестерни Здесь, вследствие наклона зубьев к образующей, дополнительно возникает еще осевое усилие. 1) - окружное усилие; 2) - радиальное усилие; 3) - осевое усилие; 4) - нормальное усилие; Силы P, R, A необходимо определить для расчета валов и подшипников, сила Pn необходима для расчета зубьев шестерен на прочность. Силу A можно уравновесить, применив сдвоенные косозубые шестерни с разнонаправленными спиралями зубьев или шевронные. в) конические прямозубые шестерни 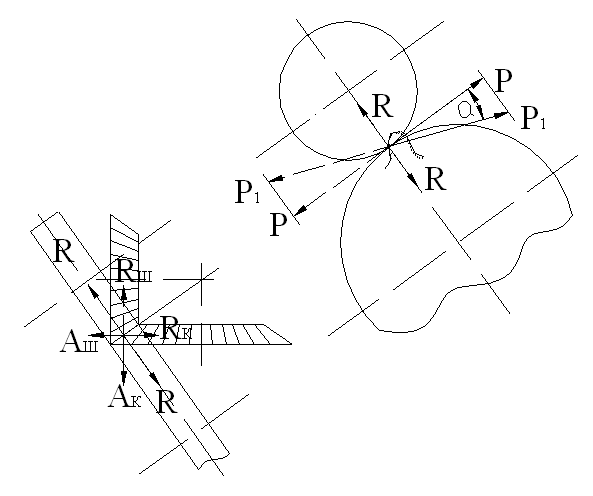 1) - окружное усилие; 2) Aш = Rк = R singш = P tga singш - осевое усилие для шестерни или радиальное для колеса; 3) Rш = Aк = R cosgш = P tga cosgш - радиальное усилие для шестерни или осевое для колеса; - нормальное усилие; Силы Р, Aш, Rш - для расчета валов и подшипников, cила Рn - для расчета зубьев на прочность. Здесь: dэ, Zэ - диаметры и числа зубьев эквивалентных цилиндрических колес. Воображаемые эквивалентные цилиндрические колеса строятся в плоскости мгновенного зацепления основных конических колес так, что оси тех и других совпадают. Работают эти колеса точно так же, как и основные конические, поэтому такое построение удобно использовать для выяснения действующих сил и напряжений в конических колесах. Расчет зубьев цилиндрических прямозубых шестерен 1. Расчет на контактную прочность поверхности зубьев Расчет базируется на известной формуле Герца для контактного сжатия цилиндров с параллельными осями: Характерными особенностями контактного сжатия являются: а) весьма ограниченная площадь контакта я а связи с этим высокие напряжения; б) объемный характер напряженного состояния; в) эллиптическая эпюра контактных напряжений, распространяющаяся только на зону контакта. Теоретически интенсивность нагрузки: Выразим rк и rк через межцентровое расстояние А: тогда В действительности расчетная интенсивность нагрузки будет отличаться от теоретической на величину поправочных коэффициентов Кк и Кд. 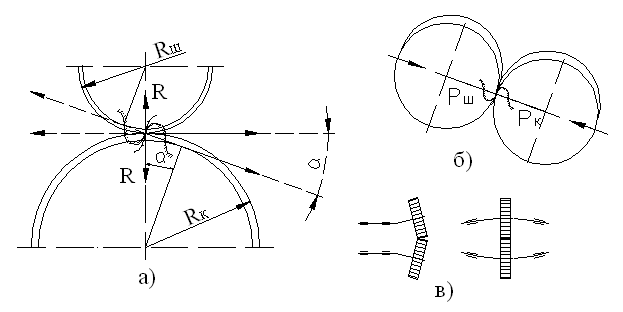 Рис. 1  Здесь: Кк - коэффициент концентрации нагрузки, выражающий неполноту контакта по линии. Он зависит от деформации валов (рис. 1 в) и ширины шестерен. Кд - коэффициент динамичности нагрузки, зависящий от окружной скорости и чистоты обработки поверхности зубьев. Приведенная кривизна зубьев шестерен в точке контакта (рис. 1 б). (Знак минус для внутреннего зацепления). Здесь: rш и rк - мгновенные радиусы кривизны в полосе зацепления.  .Приведенный модуль упругости: . Здесь: Еш и Ек - модули упругости материала шестерни и колеса. Если обе шестерни изготовлены из одного материала, то в формулу подставляется: Подставляя в основную формулу все величины, получим:  Выразив крутящий момент на оси колеса через мощность в кВт:  E = 2,1*106 Получаем проверочную формулу в окончательном виде: 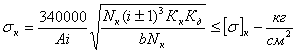 или 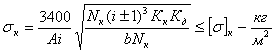 По этой формуле можно проверить и сравнить с допускаемыми, действующие в данной передаче, контактные напряжения. Для проектного расчета эта формула преобразуется, для чего ширина шестерни выражается через межцентровое расстояние. Коэффициент относительной ширины , тогда: 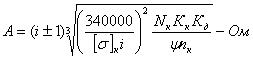 Для редукторов в среднем y = 0,2 + 0,4. Для коробок передач y = 0,1 + 0,2. Здесь: b - ширина шестерни в см; А - межцентровое расстояние в см; nк - число оборотов в минуту вала колеса; N - мощность на валу колеса в кВт; [s] - допускаемое контактное напряжение. По полученной величине межцентрового расстояния можно подобрать модуль, задавшись числом зубьев малой шестерни Zш = 17 - 25 (с коррекцией Z ³ 14). Определение допускаемых контактных напряжений При циклических нагрузках допускаемые напряжения зависят не только от материала и термообработки, но также и от числа циклов нагружения (времени работы), которое в формуле фигурирует в виде коэффициента режима нагрузки Кр. [s]к = [s]таб Кр где [s]таб - табличное допускаемое напряжение; [s]таб = С1 Нб - для улучшенных сталей; [s]таб = С2 HRc - для цементированных и закаленных сталей. Здесь: С1 и С2 - табличные коэффициенты, зависящие от принятого материала и термообработки. При постоянном режиме нагрузки: Nц = 60nt – число циклов нагружения. При переменном режиме нагрузки:  .где Mi, ni, ti - крутящий момент, число оборотов и время работы в часах на каждый ступени усредненного графика нагрузки. Минимальные значения Кp ограничены наступлением длительного предела выносливости. Для улучшенных сталей Кp ³1, для цементированных и закаленных сталей Кp ³ 0,59. 2. Расчет на усталостный изгиб зубьев Опасным нагружением считается такое, которое соответствует моменту начала входа зуба в зацепление. Интенсивность нагрузки qp создает две составляющие, из которых одна сжимает, а другая нагибает зуб. Опасным сечением считается сечение у корня зуба со стороны растянутых волокон, так как закаленные стальные зубья слабее сопротивляются растяжению, чем сжатию. al - угол зацепления при вершине зуба. 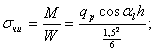 b = 1. Входящие в эти формулы величины S, h и al аналитически трудно определимы, поэтому формула преобразуется так, чтобы в скобках были безразмерные величины, совокупность которых определяется по таблицам или графикам: 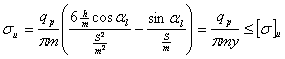 Здесь: y - коэффициент формы зуба; определяется по таблицам или графикам в зависимости от числа зубьев и коэффициента коррекции (если она есть). 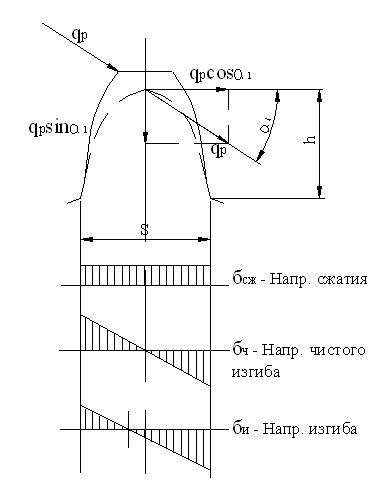 Подставив значение q, введенное ранее, получаем проверочную формулу:  Для проектных расчетов формула преобразуется с введением коэффициента относительной модульной ширины шестерни: обычно yм = 6 –10 Выражая величины А и b через модуль, получаем проектную формулу: 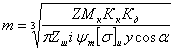 Обычно шестерни закрытых передач рассчитываются на контактную прочность (опасным является питинг) и проверяются на изгиб; шестерни открытых передач, для которых питинг не опасен, рассчитываются только на изгиб. Определение допускаемых напряжений изгиба Допускаемые напряжения определяются как часть от предела усталости (выносливости) материала при симметричном цикле нагружения: - для нереверсивных передач; - для реверсивных передач. Здесь: n1 - коэффициент запаса прочности по пределу усталости, Кs - коэффициент концентрации напряжений у ножки зуба, Kрн - коэффициент режима нагрузки по изгибу, можно принимать его равным 1 для большинства передач (только для очень тихоходных передач он может быть больше единицы). Особенности расчета косозубых цилиндрических шестерен 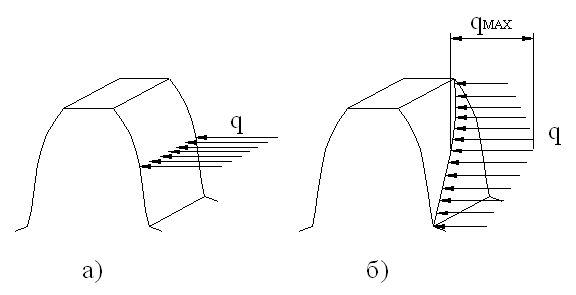 Рис.2 Принципиально расчетные формулы для косозубых шестерен те же, что и для прямозубых, отличие заключается в следующем: Таблица 2
Неравномерность эпюры является положительным фактором, спасая зубья от кромочных давлений при небольшом перекосе ее в зацеплении; она является следствием неравной жесткости головки и ножки зуба. Особенности расчета конических прямозубых шестерен Конические шестерни рассчитываются как эквивалентные им цилиндрические. Окружное усилие определяется по среднему диаметру, расчетным является средний модуль. При определении коэффициента формы зуба принимается эквивалентное число зубьев. Коррекция зубьев шестерен  В целях уменьшения габаритов и веса машин желательно у малых шестерен число зубьев делать минимальным, однако этому препятствует подрез ножки зуба, который для эвольвентного двадцатиградусного зацепления имеет место при Z < 17 зубьев. Вводя коррекцию (теоретическое исправление профиля), можно уменьшить Zmin до 14 зубьев и даже менее. 1. Угловая коррекция (фау-коррекция) заключается в смещении профиля зубьев малой шестерни в плюс (от центра) на величину: V = xm где x - коэффициент коррекции. При этом увеличивается на величину V межцентровое расстояние, а также угол зацепления, так как при раздвижке центров раздвигаются соответственно и основные окружности, к которым касательна линия зацепления. 2. Высотная коррекция (фау-нуль-коррекция), при которой профиль зубьев малой шестерни смещается в плюс (+V), а профиль зубьев колеса на столько же - в минус (-V). При этом межцентровое расстояние и угол зацепление не меняются, изменяются лишь относительная высота головки и ножки зубьев. Изготовление корригированных шестерен не представляет никаких трудностей. КПД зубчатых передач Для закрытых передач в среднем: цилиндрических h =0,98, конических h = 0,97. Для открытых передач: цилиндрических h = 0,97, конических h = 0,96 . Эти цифры включают также потери в опорах качения, которые невелики и составляют от 0,25 до 0,5 % на опору при надежной смазке. Планетарные зубчатые передачи Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси. П  ланетарные передачи имеют ряд преимуществ перед обычными:+ большие передаточные отношения при малых габаритах и массе; + возможность сложения или разложения механической мощности; + лёгкое управление и регулирование скорости; + малый шум вследствие замыкания сил в механизме. В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом aw = 30о. Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом). Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач. Волновые зубчатые передачи П  редставляют собой цилиндрические передачи, где одно из колёс имеет гибкий венец. Этот гибкий венец деформируется генератором волн специальной некруглой формы и входит в зацепление с центральным колесом в двух зонах.Идея волновых передач заключается в наличии нескольких пар зацепления, которые ещё и перемещаются по окружности, за счёт чего достигается огромное передаточное отношение (обычно U 60 ¸ 300, известны конструкции с U > 1000). И это в одной ступени! П 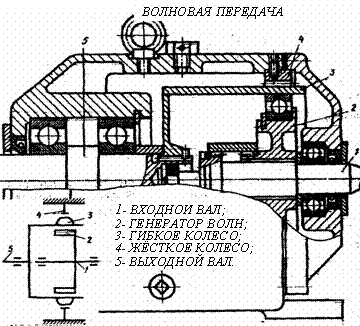 ринцип работы волновой передачи аналогичен работе планетарной передачи с внутренним зацеплением и деформируемым сателлитом.Такая передача была запатентована американским инженером Массером в 1959 г. Волновые передачи имеют меньшие массу и габариты, большую кинематическую точность, меньший мёртвый ход, высокую вибропрочность за счёт демпфирования (рассеяния энергии) колебаний, создают меньший шум. При необходимости такие передачи позволяют передавать движение в герметичное пространство без применения уплотняющих сальников, что особенно ценно для авиационной, космической и подводной техники, а также для машин химической промышленности. К недостаткам волновых передач относятся: ` ограниченные обороты ведущего вала (во избежание больших центробежных сил инерции некруглого генератора волн); ` мелкие модули зубьев (1,5 – 2 мм); ` практически индивидуальное, дорогостоящее, весьма трудоёмкое изготовление гибкого колеса и генератора. Основные виды поломок волновых передач: · разрушение подшипника генератора волн от нагрузки в зацеплении; · проскакивание генератора волн при больших вращающих моментах, когда зубья на входе в зацепление упираются друг в друга вершинами; · поломка гибкого колеса от трещин усталости (особенно при U < 80); · износ зубьев на концах; · пластические деформации боковых поверхностей зубьев при перегрузках. Расчёт волновых зубчатых передач отличается от расчёта обычных зубчатых передач тем, что учитывается деформация гибкого венца и генератора. За критерий работоспособности обычно принимают допускаемые напряжения смятия  ;  ,где Yd – коэффициент ширины гибкого венца; d – делительный диаметр гибкого венца. Зацепления Новикова Итак, основной недостаток зубчатых передач с эвольвентным профилем (цилиндрических, конических, планетарных, волновых) – высокие контактные напряжения в зубьях. Они велики потому, что контактируют два зуба с выпуклыми профилями. При этом площадка контакта очень мала, а контактные напряжения соответственно высоки. Это обстоятельство сильно ограничивает "несущую способность" передач, т.е. не позволяет передавать большие вращающие моменты. Р  ешая проблемы проектирования тяжёлых тихоходных машин, таких как трактора и танки, М.Л. Новиков в 1954 году разработал зацепления, в которых выпуклые зубья шестерни зацепляются с вогнутыми зубьями колеса.К тому же выпуклый и вогнутый профили (обычно круговые) имеют близкие по абсолютной величине радиусы кривизны. За счёт этого получается большая площадка контакта, контактные напряжения уменьшаются и появляется возможность передавать примерно в 1,4 ¸ 1,8 раза большие вращающие моменты. К сожалению, при этом приходится пожертвовать основным достоинством эвольвентных зацеплений – качением профилей зубьев друг по другу и соответственно получить высокое трение в зубьях. Однако для тихоходных м  ашин это не так важно.Рабочие боковые поверхности зубьев представляют собой круговинтовые поверхности, поэтому передачи можно называть круговинтовыми. В дальнейшем был разработан вариант передачи с двумя линиями зацепления. В ней зубья каждого колеса имеют вогнутые ножки и выпуклые головки. Передачи с двумя линиями зацепления обладают большей несущей способностью, менее чувствительны к смещению осей, работают с меньшим шумом и более технологичны. Эти передачи успешно применяются при малых числах зубьев (Z1 < 10) и дают достаточную жёсткость шестерён при их большой относительной ширине. Зацепления Новикова в редукторах применяют вместо перехода на колёса с твёрдыми поверхностями. Расчёт передач Новикова на контактную прочность проводят на основе формулы Герца-Беляева, учитывая экспериментально установленный факт, что несущая способность передач при прочих равных условиях обратно пропорциональна синусу угла наклона зубьев. Кроме того, в расчёте немного завышаются допускаемые напряжения. Передачи бывают однопарные, применяемые в редукторах общего назначения и многопарные, получаемые за счёт увеличения осевого размера и применяемые в прокатных станах, редукторах турбин и т.п. Конические зубчатые передачи Передают вращающий момент между валами с пересекающимися осями (чаще всего под углом 900). Их зубья бывают прямыми, косыми, круговыми и обычно имеют эвольвентный профиль. И  хотя, конические колёса сложнее цилиндрических как по своей геометрии, так и в изготовлении, принципы силового взаимодействия, условия работы, а следовательно, и методика расчёта аналогичны цилиндрическим.Здесь мы рассмотрим только отличительные особенности расчёта конических колёс. Сначала конструктор выбирает внешний окружной модуль mte, из которого рассчитывается вся геометрия зацепления, в частности, нормальный модуль в с 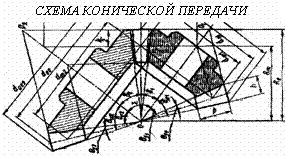 ередине зубаmnm= mte (1 – 0,5 b/Re), где Re – внешнее конусное расстояние. Силы в конической передаче действуют аналогично цилиндрической, однако следует помнить, что из-за перпендикулярности осей радиальная сила на шестерне аналогична осевой силе для колеса и наоборот, а окружная сила при переходе от шестерни к колесу только меняет знак  ; .Прочностные расчёты конических колёс проводят аналогично цилиндрическим, по той же методике. Из условия контактной выносливости определяют внешний делительный диаметр dwe, из условия прочности на изгиб находят нормальный модуль в середине зуба mnm. При этом в расчёт принимаются воображаемые эквивалентные колёса с числами зубьев Zэ1,2 =Z1,2 / cosd1,2 и диаметрыdэ1,2 = mte Z1,2 / cosd1,2. Здесь Z1, Z2, - фактические числа зубьев конических колёс. При этом числа Zэ1,2могут быть дробными. В эквивалентных цилиндрических колёсах диаметр начальной окружности и модуль соответствуют среднему сечению конического зуба, вместо межосевого расстояния берётся среднее конусное расстояние, а профили эквивалентных зубьев получают развёрткой дополнительного конуса на плоскость. Червячные передачи Относятся в передачам со скрещивающимся осями (рис.3). Она состоит из червяка – винта с трапецеидальной резьбой и зубчатого червячного колеса с зубьями соответствующей специфической формы. Движение в червячной передаче преобразуется по принципу винтовой пары. С положительной стороны червячные передачи характеризуются малыми габаритами, большим передаточный отношением в одной паре и бесшумной работой, однако, вследствие больших потерь мощности на трение в зацеплении, КПД их сравнительно низок и составляет 0,60 + 0,85 (в среднем 0,7 - 0,8). Потери мощности на трение вызывают значительное выделение тепла, которое необходимо отводить от стенок корпуса. Это обстоятельство ограничивает мощность практически применяемых передач пределом 10-20 кВт, зато для малых мощностей эти передачи нашли самое широкое применение. В отличие от эвольвентных зацеплений, где преобладает контактное качение, виток червяка скользит по зубу колеса. Следовательно, червячные передачи имеют "по определению" один фундаментальный недостаток: высокое трение в зацеплении. Это ведёт к низкому КПД (на 20-30% ниже, чем у зубчатых), износу, нагреву и необходимости применять дорогие антифрикционные материалы. Кроме того, помимо достоинств и недостатков, червячные передачи имеют важное свойство: движение передаётся только от червяка к колесу, а не наоборот. Никакой вращающий момент, приложенный к колесу, не заставит вращаться червяк. Именно поэтому червячные передачи находят применение в подъёмных механизмах, например в лифтах. Там электродвигатель соединён с червяком, а трос пассажирской кабины намотан на вал червячного колеса во избежание самопроизвольного опускания или падения. Это свойство не надо путать с реверсивностью механизма. Ведь направление вращения червяка может быть любым, приводя либо к подъёму, либо к спуску той же лифтовой кабины. Передаточное отношение червячной передачи находят аналогично цилиндрической U = n1 / n2 = Z2 / Z1. Здесь Z2 – число зубьев колеса, а роль числа зубьев шестерни Z1 выполняет число заходов червяка, которое обычно бывает равно 1, 2, 3 или 4. Очевидно, что однозаходный червяк даёт наибольшее передаточное отношение, однако наивысший КПД достигается при многозаходных червяках, что связано с уменьшением трения за счёт роста угла трения. Для увеличения КПД передачи: 1) червяк должен иметь твердую, очень чисто обработанную поверхность зубьев (желательна полировка). Материалом для червяков служат высокоуглеродистые - калимые или мало углеродистые цементированные стали, например, Ст.У-7, У-8, Ст.50 или Ст.20Х, Ст.18ХГТ, Ст.20ХНЗА; 2) венец червячного колеса должен быть изготовлен из антифрикционного материала - бронзы; 3) смазка должна быть обильной в закрытом пыленепроницаемом корпусе. В СССР стандартизован архимедов червяк (рис.4), который так называется потому, что в торцевом сечении зуб очерчен архимедовой спиралью, а в осевом - прямой, наклонной под углом зацепления a = 20°. В конволютном червяке режущий инструмент (или наждачный круг) установлен вдоль оси спирали зуба; это удобно при массовом производстве червяков, так как позволяет производить одновременную шлифовку двух сторон профиля зубьев. Эвольвентные червяки применяются сравнительно редко, в них зуб по боковым поверхностям очерчен эвольвентами. Основные причины выхода из строя червячных передач: r поверхностное выкрашивание и схватывание; r излом зуба. Это напоминает характерные дефекты зубчатых передач, поэтому и расчёты проводятся аналогично. 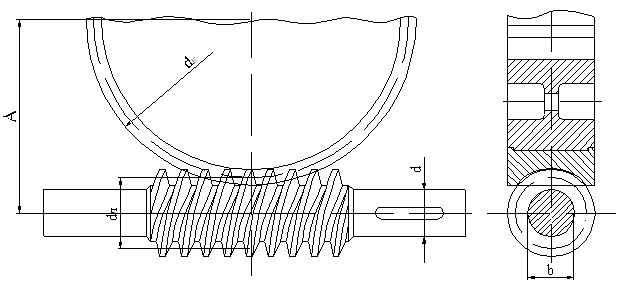 Рис. 3 Геометрическая форма червяков 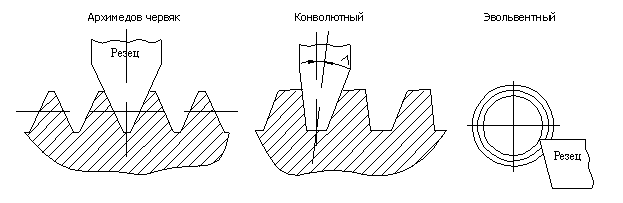 Рис. 4 Расчетные геометрические зависимости 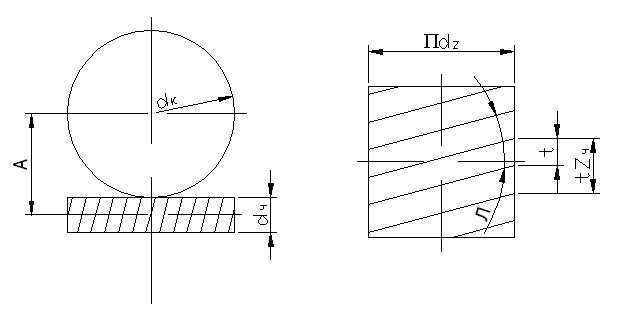 Рис. 5 aк и aч - диаметры делительных окружностей колеса в червяка; t и m - шаг и модуль (осевой); Zк Zч - число зубьев колеса и число заходов червяка; Zч = 1 + 4, обычно Zч = 1 + 2; l - угол спирала зуба червяка; qч- относительный диаметр червяка; qч = 8 –13. 1. Передаточное отношение: 2. Угол наклона спирали нарезки зубьев: 3. Диаметры: 4. Межцентровое расстояние:  5. Размеры зубьев: hч = m, hн =1,2m, КПД червячной передачи Рассматривая червяк как винт с модульной нарезкой, пренебрегая за малостью потерями в опорах качения, на основании ранее выведенной формулы можно написать: - угол трения. 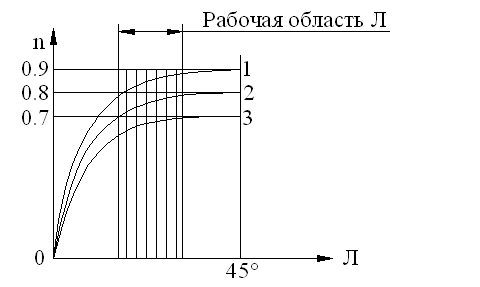 Рис.6 1 - очень хорошие условия - h = 0,8 - 0,85. 2 - средние условия - h = 0,7 - 0,8. 3 - плохие условия (чугунное колесо) - h = 0,6 - 0,7. Из графика функции (рис.6) видно, что теоретически наивыгоднейшим будет угол l, близкий к 45°, но при таких углах очень велики осевые нагрузки на подшипники колеса, поэтому, учитывая пологость кривых в зоне больших углов, практически принимают рабочую область углов l в пределах, соответствующих Zч = 1 + 4. Силы, действующие в зацеплении червячной передачи Червячное колесо можно рассматривать как косозубую цилиндрическую шестерню, а схему сил в червячной передаче уподобить схеме сил в косозубых шестернях; отличие заключается лишь в том, что главная нормаль в червячной передаче смещена на угол трения r, который достаточно велик и им пренебрегать нельзя. 1. Окружное усилие для колеса иди осевое - для червяка: 2. Осевое усилие для колеса или окружное - для червяка: 3. Радиальное усилие: Главная нормаль: По силам: A, P и R рассчитываются валы и подшипники, сила Рn служит для расчета на прочность зубьев колеса. Тепловой расчет червячной передачи Вследствие нагрева, вызванного трением, червячные передачи нуждаются также и в тепловом расчёте. Практика показывает, что механизм опасно нагревать выше 95оС. Допускаемая температура назначается 65 oC. Уравнение для теплового расчёта составляется из баланса тепловой энергии, а именно: выделяемое червячной парой тепло должно полностью отводиться в окружающую среду Qвыделяемое = Qотводимое. Решая это уравнение, находим температуру редуктора, передающего заданную мощность N t = [860N(1-η)] / [KT S(1-Ψ)] + to. где KT – коэффициент теплоотдачи, S – поверхность охлаждения (корпус), to – температура окружающей среды, Y – коэффициент теплоотвода в пол. В случае, когда расчётная температура превышает допускаемую, то следует предусмотреть отвод избыточной теплоты. Это достигается оребрением редуктора, искусственной вентиляцией, змеевиками с охлаждающей жидкостью в масляной ванне и т.д. 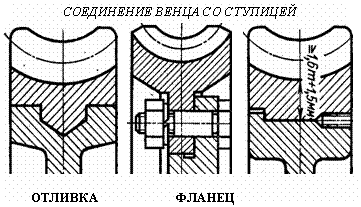 Оптимальная пара трения это "сталь по бронзе". Поэтому при стальном червяке червячные колёса должны выполняться из бронзовых сплавов. Однако цветные металлы дороги и поэтому из бронзы выполняется лишь зубчатый венец, который крепится на сравнительно дешёвой стальной ступице. Таким образом, червячное колесо - сборочная единица, где самые популярные способы крепления венца это либо центробежное литьё в кольцевую канавку ступицы; либо крепление венца к ступице болтами за фланец; либо посадка с натягом и стопорение винтами для предотвращения взаимного смещения венца и ступицы.Крепление венца к ступице должно обеспечивать фиксацию как от проворота (осевая сила червяка = окружной силе колеса), так и от осевого "снятия" венца (окружная сила червяка = осевой силе колеса). Вопросы для самопроверки - Каково назначение передач в машинах ? - Каковы области применения прямозубых и косозубых передач ? - Каковы сравнительные достоинства прямозубых и косозубых колёс ? - Как определяется передаточное отношение и передаточное число ? - Каковы главные виды разрушений зубчатых колёс ? - Какие силы действуют в зубчатом зацеплении ? - Какие допущения принимаются при расчёте зубьев на контактную прочность ? - По какой расчётной схеме выполняется расчёт зубьев на изгиб ? - В чём заключаются достоинства и недостатки планетарных передач ? - Для чего созданы волновые передачи и в чём заключается принцип их работы ? - В чём заключаются достоинства и недостатки волновых передач ? - Для чего созданы зацепления Новикова и в чём заключается принцип конструкции их зубьев ? - В чём заключаются достоинства и недостатки зацеплений Новикова ? - В чём заключается принцип конструкции червячной передачи ? - Каковы достоинства и недостатки червячных передач ? - Какое свойство червячной передачи отличает её от других передач ? - Каковы основные причины поломок червячных передач ? - Из каких условий находят температуру червячной передачи ? - Какие методы могут применяться для снижения температуры червячной передачи ? - Какие материалы должны применяться для червячной передачи ? - Каковы особенности конструкции червячных колёс ? |
