логика Гетманова. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
 Скачать 2.45 Mb. Скачать 2.45 Mb.
|
|
§ 4. ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ1 Категорический силлогизм — это вид дедуктивного умозаключения, в котором из двух истинных категорических суждений, где Sи Р связаны средним термином, при соблюдении правил необходимо следует заключение. Силлогизм происходит от греческого syllogismos (сосчитывание, выведение следствия). В составе категорического силлогизма имеются две посылки и заключение. Все металлы (М) электропроводны (Р) — большая посылка. Медь (S) есть металл (М) — меньшая посылка. Медь (S) электропроводна (Р) — заключение. Понятия, входящие в состав силлогизма, называются терминами силлогизма. В приведенном примере терминами являются: Р («электропроводник») — больший термин, это предикат заключения; S(«медь») — меньший термин, это субъект заключения; М («металл») — средний термин, служащий в посылках для связывания Sи Р и отсутствующий в заключении (рис. 43). 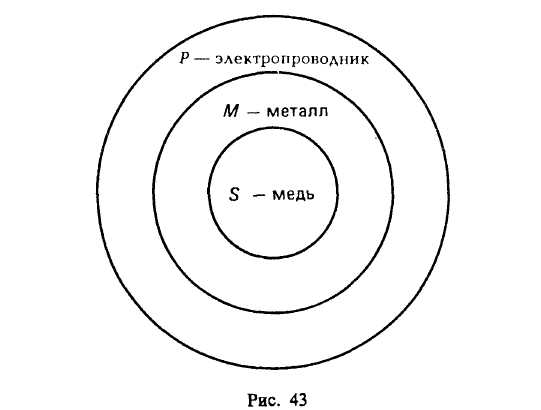 Посылка, содержащая предикат заключения (т. е. больший термин), называется большей посылкой. Посылка, содержащая субъект заключения (т. е. меньший термин), называется меньшей посылкой. В основе вывода по категорическому силлогизму лежит аксиома силлогизма. «Все, что утверждается (отрицается) о роде (или классе), необходимо утверждается (отрицается) о виде (или о члене данного класса), принадлежащем к данному роду». Иными словами: то, что мы утверждаем о металле как роде, мы утверждаем и о его виде — меди, а именно утверждаем его признак «быть электропроводником». Фигуры категорического силлогизма Фигурами категорического силлогизма называются формы силлогизма, различаемые по положению среднего термина М в посылках. Различаются четыре фигуры (рис. 44). 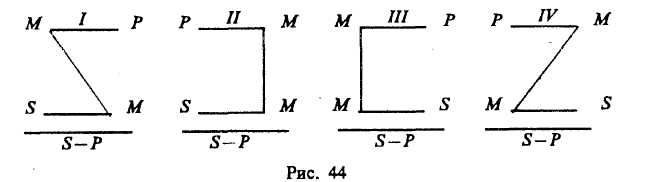 Примеры: 1. Все злаки (М) — растения (Р). 2. Все ужи (Р) — пресмыкающиеся (М). Рожь (S) — злак (М). Это животное (S) не является пре- _____________________________ смыкающимся (М). Рожь (S) — растение (Р). ------------------------------------------- 3. Все углероды (М) — простые Это животное (S) не является ужом(Р). тела (Р). Все углероды (М) — электро- 4. Все киты (Р) — млекопитающие (М). проводны (S). Ни одно млекопитающее (М) не есть рыба (5). __________________________ ------------------------------------------------ Некоторые электропроводники Ни одна рыба (S) не есть кит (Р). (S) — простые тела (Р). Особые правила фигур I фигура. Большая посылка должна быть общей, меньшая — утвердительной. II фигура. Большая посылка общая и одна из посылок, а также заключение отрицательные. III фигура. Меньшая посылка должна быть утвердительной, а заключение — частное. IV фигура. Общеутвердительных заключений не дает. Модусы категорического силлогизма Модусами фигур категорического силлогизма называются разновидности силлогизма, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключения. Всего правильных модусов в четырех фигурах 19. I фигура имеет следующие правильные модусы (буквы обозначают последовательно количество и качество большей посылки, меньшей и заключения): ААА, ЕАЕ, All, ЕЮ. Пример 1 иллюстрирует модус ААА. II фигура имеет правильные модусы: АЕЕ, АОО, ЕАЕ, ЕIО. Умозаключение 2 построено по модусу АЕЕ. III фигура имеет правильные модусы: AAI, EAO, IAI, ОАО, АП, ЕЮ. Модус AAIпредставлен примером 3. IV фигура имеет правильные модусы: AAI, АЕЕ, IAI, EAO, ЕЮ. Модус АЕЕ представлен примером 4. Правила категорического силлогизма Категорические силлогизмы в мышлении встречаются весьма часто. Для того чтобы получить истинное заключение, необходимо брать истинные посылки и соблюдать перечисленные ниже правила категорического силлогизма (так же как и особые правила фигур категорического силлогизма, перечисленные ранее). I. Правила терминов 1. В каждом силлогизме должно быть только три термина (S, Р, М). Ошибка называется «учетверение терминов». Ошибочное умозаключение: Движение вечно. Хождение в институт — движение. ------------------------------------------ Хождение в институт вечно. Здесь «движение» трактуется в разном смысле — в философском и обыденном. 2. Средний термин должен быть распределен по крайней мере в одной из посылок. Некоторые растения (М) ядовиты (Р). Белые грибы (S) — растения (М). ------------------------------------------ Белые грибы (S) —- ядовиты (Р). Здесь средний термин «растение» не распределен ни в одной из посылок, поэтому заключение ложное. 3. Термин распределен в заключении, если и только если он распределен в посылке. Иначе в терминах заключения говорилось бы больше, чем в терминах посылок. Во всех городах за полярным кругом бывают белые ночи. Санкт-Петербург не находится за полярным кругом. ------------------------------------------- В Санкт-Петербурге не бывает белых ночей. Заключение ложное, так как нарушено данное правило. Предикат вывода в заключении распределен, а в посылке он не распределен, следовательно, произошло расширение большего термина. II. Правила посылок 4. Из двух отрицательных посылок нельзя сделать никакого заключения. Например: Дельфины не рыбы. Щуки не дельфины. ------------------------------------ ? 5. Если одна из посылок отрицательная, то и заключение должно быть отрицательным. Все моржи — ластоногие. Это животное не является ластоногим. ------------------------------------- Это животное не является моржом. 6. Из двух частных посылок нельзя сделать заключение. Некоторые животные — пресмыкающиеся. Некоторые живые организмы — животные. ----------------------------------------------- ? 7. Если одна из посылок частная, то заключение должно быть частным. Все спекулянты подлежат наказанию. Некоторые люди — спекулянты. ------------------------------------------------ Некоторые люди подлежат наказанию. Наиболее распространенные ошибки при умозаключении по категорическому силлогизму такие: 1. Заключение делается по I фигуре с меньшей отрицательной посылкой. Приведем два примера. Все классные комнаты нуждаются в проветривании. Эта комната — не классная. ---------------------------------------- Эта комната не нуждается в проветривании. Все студенты сдают экзамены. Смирнов не является студентом. ---------------------------------------- Смирнов не сдает экзамены. Заключение не следует с необходимостью из посылок, так как вторая посылка должна быть утвердительной. 2. Заключение делается по II фигуре с двумя утвердительными посылками. Все зебры полосатые. Это животное полосатое. -------------------------------- Это животное — зебра. Заключение не следует с необходимостью из этих посылок, так как одна из посылок и заключение должны быть отрицательными суждениями. § 5. СОКРАЩЕННЫЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ (ЭНТИМЕМА) Энтимемой, или сокращенным категорическим силлогизмом, называется силлогизм, в котором пропущена одна из посылок или заключение. Термин «энтимема» в переводе с греческого языка означает «в уме», «в мыслях». Примером энтимемы является такое умозаключение: «Все кашалоты — киты, следовательно, все кашалоты — млекопитающие». В этой энтимеме пропущена большая посылка. Восстановив энтимему до полного категорического силлогизма, имеем: Все киты — млекопитающие. Все кашалоты — киты. ----------------------------------------- Все кашалоты — млекопитающие. Приведем пример энтимемы, в которой пропущена меньшая посылка: «Все металлы теплопроводны, следовательно, и алюминий теплопроводен». Восстановим энтимему: Все металлы теплопроводны. Алюминий — металл. ----------------------------------------- Алюминий теплопроводен. Приведем энтимему, в которой пропущено заключение: «Все рыбы дышат жабрами, а окунь — рыба». При восстановлении энтимемы надо, во-первых, определить, какое суждение является посылкой, а какое — заключением. Посылка обычно стоит после союзов «так как», «потому что», «ибо» и т. п., а заключение стоит после слов «следовательно», «поэтому», «потому» и т. д. Студентам дается энтимема: «Этот физический процесс не является испарением, так как не происходит перехода вещества из жидкости в пар». Они восстанавливают эту энтимему, т. е. формулируют полный категорический силлогизм. Суждение, стоящее после слов «так как», является посылкой. В энтимеме пропущена большая посылка, которую студенты формулируют на основе знаний о физических процессах. Испарение есть процесс перехода вещества из жидкости в пар. Этот физический процесс не есть процесс перехода вещества из жидкости в пар. -------------------------------------------------------- Этот физический процесс не есть испарение. Данный категорический силлогизм построен по II фигуре; особые правила ее соблюдены, так как одна из посылок и заключение отрицательные, большая посылка общая, представляющая собой определение понятия «испарение». Энтимемами пользуются чаще, чем полными категорическими силлогизмами. § 6. СЛОЖНЫЕ И СЛОЖНОСОКРАЩЕННЫЕ СИЛЛОГИЗМЫ (ПОЛИСИЛЛОГИЗМЫ, СОРИТЫ, ЭПИХЕЙРЕМА) Полисиллогизмом (сложным силлогизмом) называются два или несколько простых категорических силлогизмов, связанных друг с другом таким образом, что заключение одного из них становится посылкой другого. Различают прогрессивные и регрессивные полисиллогизмы. В прогрессивном полисиллогизме заключение предшествующего силлогизма становится большей посылкой последующего силлогизма. Приведем пример прогрессивного полисиллогизма, представляющего собой цепь из трех силлогизмов и имеющего такую схему:  Возьмем полисиллогизм, состоящий из двух силлогизмов, и справа запишем его схему.  Разъясним получение схемы 2. Если общие категорические суждения заменить совпадающими с ними по смыслу условными суждениями, то второй полисиллогизм примет следующий вид: Если предмет есть металл, то он теплопроводен. Если предмет есть щелочноземельный металл, то он, конечно, металл. Если предмет есть щелочноземельный металл, то он теплопроводен. Если предмет есть кальций, то он щелочноземельный металл. Значит, если предмет есть кальций, то он теплопроводен. Выразив суждение «Предмет есть металл» буквой а, суждение «Предмет теплопроводен» — буквой b, суждение «Предмет есть щелочноземельный металл» — буквой с, суждение «Предмет есть кальций» — буквой d, мы получим схему 2.В виде правила вывода схему 2 данного прогрессивного полисиллогизма можно записать так: где— знак вывода. Это правило вывода путем преобразований можно перевести в формулу алгебры логики: Эта формула тождественно-истинна, если все посылки полисиллогизма являются общими суждениями. Регрессивный полисиллогизм — это такой сложный силлогизм, в котором заключение предшествующего силлогизма становится меньшей посылкой последующего силлогизма. 1. Всеорганизмы (В) суть тела (С). 2. Все тела (С) имеют вес (D). Все растения (А) суть организмы(B) Все растения (А) суть тела (С). _____________________ _____________________ Все растения (А) суть тела (С). Все растения (А) имеют вес (D). Запишем эти два силлогизма схематически: 1. Все В суть С. 2. Все С суть D. Все А суть В. Все А суть С. _______________ ____________ Все А суть С. Все А суть D. Соединив их вместе и не повторяя дважды суждение «Все А суть С», мы получим схемы регрессивного полисиллогизма для общеутвердительных посылок: 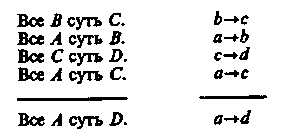 В виде правила вывода последнюю схему можно записать так: Это правило вывода путем преобразования можно перевести в формулу алгебры логики: Сорит (с общими посылками) Прогрессивный и регрессивный полисиллогизмы в мышлении чаще всего применяются в сокращенной форме — в виде соритов. Все растения (А) суть организмы (В). Все организмы (В) суть тела (С). Все тела (С) имеют вес (D). ______________________ Всякое растение (А) имеет вес (D). Схема регрессивного сорита: Все А суть В. a-> b Все В суть С. b-> c Все С суть D. c-> d ___________ _____________ все А сутьD. a->d Существуют два вида соритов: прогрессивный и регрессивный. Прогрессивный сорит получается из прогрессивного полисиллогизма путем выбрасывания заключений предшествующих силлогизмов и больших посылок последующих. Все, что укрепляет здоровье (А), полезно (В). Спорт (С) укрепляет здоровье (А). Легкая атлетика (D) — спорт (C). Бег (Е) — вид легкой атлетики (D). _________________________ Бег (E) полезен (В). Схемы прогрессивного сорита: Все А суть В. a -> b Все С суть А. c -> a Все D сутьC. d -> c Все Eсуть D. e->d ____________ ____________ Все E сутьB. e -> b Прогрессивный сорит начинается с посылки, содержащей предикат заключения, и заканчивается посылкой, содержащей субъект заключения. В виде правила вывода последнюю схему можно записать так: Это правило вывода путем преобразований можно перевести в формулу алгебры логики: Регрессивный сорит получается из регрессивного полисиллогизма путем выбрасывания заключений предшествующих силлогизмов и меньших посылок последующих. В первом категорическом силлогизме меняем местами посылки. Регрессивный сорит начинается с посылки, содержащей субъект заключения, и кончается посылкой, содержащей предикат заключения. В виде правила вывода последнюю схему можно записать так: Это правило вывода путем преобразований можно перевести в формулу алгебры логики: Эго формула алгебры логики (или исчисления высказываний), соответствующая регрессивному сориту, состоящему из трех общеутвердительных посылок. Формализация эсихейрем с общими посылками Эпихейремой в традиционной логике называется такой сложносокращенный силлогизм, обе посылки которого представляют собой сокращенные простые категорические силлогизмы (энтимемы). Схема эпихейремы, содержащей лишь общие и утвердительные высказывания, обычно записывается следующим образом: Все А суть С, так как А суть В. Все Dсуть А. так как Dсуть Е. ______________________ Все Dсуть С. Пример эпихейремы: Благородный труд (А) заслуживает уважения (С), так как благородный труд (А) способствует прогрессу общества (В). Труд учителя (D) есть благородный труд (А), так как труд учителя (D) заключается в обучении и воспитании подрастающего поколения (E). _________________________________________ Труд учителя (D) заслуживает уважения (С). Первая и вторая посылки эпихейремы представляют собой энтимемы, т, е. сокращенные категорические силлогизмы, у которых одна из посылок опущена. Выразим полностью первую и вторую посылки эпихейремы. 1. Все В суть С. 2. Все Е суть А. Все А суть В. Все Dсуть Е. Все А суть С. Все Dсуть А. Возьмем заключения первого и второго силлогизмов и сделаем их большей и меньшей посылками нового, третьего силлогизма. 3. Все А суть С. Все Dсуть А ._____________ Все Dсуть С. Восстановим полностью эпихейрему. 1. Все, что способствует прогрессу общества (В), заслуживает уважения (С). Благородный труд (А) способствует прогрессу общества (В). _____________________________________________________________________________________ Благородный труд (А) заслуживает уважения (С). 2. Обучение и воспитание подрастающего поколения (E) есть благородный труд (А). Труд учителя (D) заключается в обучении и воспитании подрастающего поколения (E). __________________________________________________________________________________ Труд учителя (D) есть благородный труд (А). Заключения первого и второго силлогизмов делаются посылками третьего силлогизма. 3. Благородный труд (А) заслуживает уважения (С). Труд учителя (D) есть благородный труд (А). _________________________________________________________________________________________________ Труд учителя (D) заслуживает уважения (С). Приведем еще один пример эпихейремы. Все рыбы (А) — позвоночные животные (С), так как рыбы (А) имеют скелет(В). Все акулы (D) — рыбы (А), так как акулы (D) дышат жабрами (Е). __________________________________________________________________________________________________________ Все акулы (D) — позвоночные животные (С). В виде правила вывода восстановленную эпихейрему можно записать так: 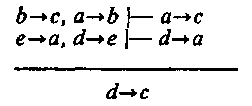 Это правило путем преобразований можно перевести в формулу: В целях большей наглядности переставим посылки и запишем эту формулу так: Можно доказать, что эта формула является законом логики. Так же как и энтимемы, сложносокращенные силлогизмы значительно упрощают наши рассуждения. Выводы, основанные на логических связях между суждениями (выводы логики высказываний) Если в логике предикатов простые суждения расчленялись на субъект и предикат, то в логике высказываний суждения не расчленяются, а рассматриваются как простые суждения, из которых с помощью логических связок (логических постоянных) образуются сложные суждения. Правила прямых выводов логики высказываний позволяют из данных истинных посылок выводить истинное заключение. На основе правил прямых выводов построены чисто условные и условно-категорические, разделительные и разделительно-категорические, а также условно-разделительные (лемматические) умозаключения. |
