логика Гетманова. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики

• Название: Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
• Анкор: логика Гетманова.doc
• Дата: 26.06.2018
• Размер: 2.45 Mb.
• Имя файла: логика Гетманова.doc
• Тип: Учебник; #20763
• страница: 12 из 25

§ 7. УСЛОВНЫЕ УМОЗАКЛЮЧЕНИЯ
Чисто условным умозаключением называется такое опосред­ствованное умозаключение, в котором обе посылки являются условными суждениями. Условным называется суждение, име­ющее структуру: «Если а, то b». Структура его такая:
Если a, то b Схема:

Если b, то c a->b, b->c

____________ ______________

Если a, то c a->c
Согласно определению логического следствия, сформулиро­ванному в рамках исчисления высказываний, если а -> с есть логи­ческое следствие из данных посылок, то, соединив посылки зна­ком конъюнкции и присоединив к ним посредством знака имп­ликации заключение, мы должны получить формулу, которая является законом логики. Формула будет такова:

Доказательство тождественной истинности этой формулы мо­жно провести табличным методом. Этот вид умозаключения часто используется в школе, в частности на уроках математики, физики и др. Приведем пример.
Если по проводнику пропустить электрический ток, то вокруг проводника образу­ется магнитное поле.

Если вокруг проводника образуется магнитное поле, то железные опилки рас­полагаются в этом магнитном поле вдоль силовых линий.

___________________________________________________________________________________________________________________Если по проводнику пропустить электрический ток, то железные опилки рас­полагаются в его магнитном поле вдоль силовых линий.
В чисто условном умозаключении существуют его разновид­ности (модусы). К ним относится, например, такой: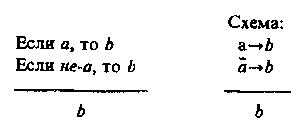



Формула:

Формула является законом логики. В этом умозаключении суждение bистинно независимо от того, утверждается или от­рицается а.

Примером такого умозаключения является следующее рас­суждение:
Если будет хорошая погода, уберем урожай.

Если не будет хорошей погоды, уберем урожай.

______________________________

Уберем урожай.
Приведем пример из художественной литературы. Один из героев Агаты Кристи, оказавшийся на острове, рассуждает: «Генерал Макартур пребывал в мрачной задумчивости. Черт побе­ри, до чего все странно! Совсем не то, на что он рассчитывал... Будь хоть малейшая возможность, он бы под любым предлогом уехал... Ни минуты здесь не остался бы... Но моторка ушла. Так что хочешь не хочешь, а придется остаться».
Условно-категорические умозаключения

Условно-категорическое умозаключение — это такое дедук­тивное умозаключение, в котором одна из посылок — условное суждение, а другая — простое категорическое суждение.

Оно имеет два правильных модуса, дающих заключение, с не­обходимостью следующее из посылок.
I. Утверждающий модус (modus ponens).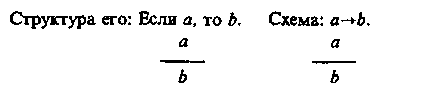



Формула (1):— является законом логики.

Можно строить достоверные умозаключения от утвержде­ния основания к утверждению следствия. Приведем два примера.
Если ты хочешь наслаждаться искусством, то ты должен быть художественно образованным человеком.

Ты хочешь наслаждаться искусством.

____________________________________

Ты должен быть художественно образованным человеком.
Для построения другого примера воспользуемся интересным высказыванием великого русского педагога К. Д. Ушинского: «Если человек избавлен от физического труда и не приучен к умственному, зверство овладевает им»² . Использовав это высказывание, построим условно-категорическое умозаключе­ние.
Если человек избавлен от физического труда и не приучен к умственному, то им овладевает зверство.

Этот человек избавлен от физического труда и не приучен к умственному.

_________________________________________

Этим человеком овладевает зверство.
Любое использование правил в русском языке, математике, физике, химии и других школьных дисциплинах основано на утверждающем модусе, дающем достоверное заключение, поэто­му в практике мышления он находит самое широкое применение.
Если этот металл натрий, то он легче воды.

Данный металл — натрий.

____________________________

Данный металл легче воды.

II. Отрицающий модус (modus tollens).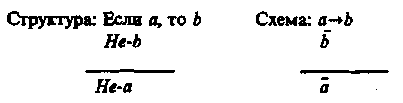



Формула (2):— также является законом логики

(это можно доказать с помощью таблицы).

Можно строить достоверные умозаключения от отрицания следствия к отрицанию основания.

Приведем два примера.
Если река выходит из берегов, то вода заливает прилегающие территории.

Вода реки не залила прилегающие территории.

____________________________

Река не вышла из берегов.
Для построения второго условно-категорического умозаключения воспользуемся следующим высказыванием: «...тот мерзок, кто ярится, если чужой он доблести свидетель» (Данте). Умозаключение построено так:
Если человек при виде чужой доблести ярится, то он мерзок.

Этот человек не является мерзким.

__________________________________

Этот человек при виде чужой доблести не ярится.
Условно-категорическое умозаключение может давать не то­лько достоверное заключение, но и вероятное.

Первый модус, не дающий достоверное заключение.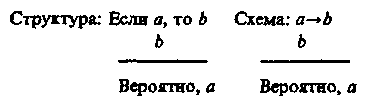



Формула (3):— не является законом логики.

Нельзя получить достоверное заключение, идя от утвержде­ния следствия к утверждению основания. Например, в умозак­лючении
Если бухта замерзла, то суда не могут входить в бухту.

Суда не могут входить в бухту.

_____________________________

Вероятно, бухта замерзла.
заключение будет лишь вероятным суждением, т. е., вероятно, бухта замерзла, но возможно, что дует сильный ветер или бухта заминирована либо существует другая причина, по которой суда не могут входить в бухту.

Вероятное заключение получится и в таком умозаключе­нии:
Если данное тело — графит, то оно электропроводно.

Данное тело электропроводно.

_____________________________

Вероятно, данное тело — графит.
Второй модус, не дающий достоверное заключение.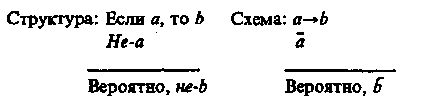



Формула (4):— не является законом логики.

Нельзя получить достоверное заключение, идя от отрицания основания к отрицанию следствия. Например:
Если человек имеет повышенную температуру, то он болен.

Этот человек не имеет повышенной температуры.

_____________________________________

Вероятно, этот человек не болен.

Люди иногда допускают логические ошибки при построении умозаключений. Они могут умозаключать так:
Если тело подвергнуть трению, то оно нагреется.

Тело не подвергли трению.

_____________________

Тело не нагрелось.
Но заключение здесь только вероятное, а не достоверное, ибо тело могло нагреться по какой-либо другой причине (от солнца, в печи и т. д.).

Заметим, что приведения такого рода примеров вполне до­статочно для того, чтобы показать, что формы умозаключений, выражаемые формулами (3) и (4), неправильны. Но никакое количество примеров применения форм, соответствующих фор­мулам (1) и (2), не в состоянии — если мы оперируем только примерами — обосновать их логическую правильность. Для та­кого обоснования требуется уже некоторая логическая теория. Такая теория, фактически отсутствующая в традиционной логи­ке, содержится в алгебре логики. Если формула, в которой ко­нъюнкция посылок и предполагаемое заключение соединены зна­ком импликации, не является тождественно-истинной, т. е. не выражает закона логики, то в умозаключении заключение не является достоверным. В таблице истинности (табл. 9) видно, что столбцы, соответствующие формулам (1) (modus ponens) и (2) (modus tollens), состоят из одних знаков «И» («истинно»); следовательно, формулы (1) и (2) выражают законы логики, а это означает, что modus ponens и modus tollens представляют собой логически правильные формы умозаключений.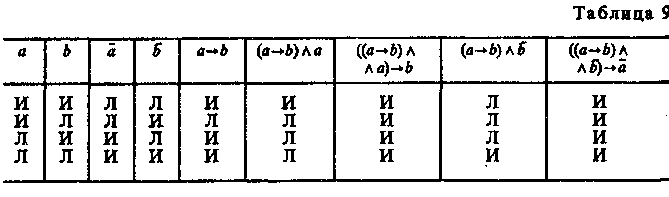


Таблицу для неправильных модусов предоставляем построить читателю. В ней наряду со знаками «И» мы увидим и знаки «Л» («ложь»), а это значит, что выражения

не являются тождественно-истинными высказываниями, т. е. законами логики.

Если умозаключение строится от утверждения следствия к ут­верждению основания, то вследствие множественности причин, из которых может вытекать одно и то же следствие, можно прийти к ложному заключению. Например, выясняя причину заболевания человека, надо перебрать все возможные причины: простудился, переутомился, был в контакте с бациллоносителем и т. д.
§ 8. РАЗДЕЛИТЕЛЬНЫЕ УМОЗАКЛЮЧЕНИЯ
Разделительным называется умозаключение, в котором одна или несколько посылок — разделительные (дизъюнктивные) суж­дения. Существуют чисто разделительные и разделительно-кате­горические умозаключения.

В чисто разделительном умозаключении обе (или все) посыл­ки являются разделительными суждениями.

В традиционной логике принята следующая его структура:
Sесть А, или В, или С.

А есть или А₁, или A₂.

________________________

Sесть или А₁, или A₂, или В, или С.
В первом разделительном суждении каждое из трех простых суждений: Sесть A, Sесть В, Sесть С — называется альтер­нативой. Из суждения «Sесть А» образуются еще две альтер­нативы, которые составляют два члена новой дизъюнкции.

Например:
Всякая философская система есть или идеализм, или материализм.

Идеалистическая система является или объективным, или субъективным идеализмом.

________________________________________________________________________________________

Всякая философская система есть или объективный идеализм, или субъектив­ный идеализм, или материализм.
В разделительно-категорическом умозаключении одна посыл­ка — разделительное суждение, другая — простое категоричес­кое суждение. Этот вид умозаключения содержит два модуса.

I модус — утверждающе-отрицающий (modus ponendo tollens).
Данный глагол может стоять или в настоящем, или в прошедшем, или в будущем

времени.

Данный глагол стоит в настоящем времени.

_____________________________________________

Данный глагол не стоит ни в будущем, ни в прошедшем времени.
Заменив конкретные высказывания в посылках и заключении переменными, получим запись этого модуса (с двумя членами дизъюнкции) в терминах символической логики в виде правила вывода:



В этом модусе союз «или» употребляется в смысле строгой дизъюнкции. Формулы, соответствующие этому модусу, имеют вид:

1)

Обе эти формулы выражают законы логики.

Если в этом модусе союз «или» взят в смысле нестрогой дизъюнкции, то формулы (3) и (4), сооветствующие этому моду­су, не будут выражать закон логики.

3) 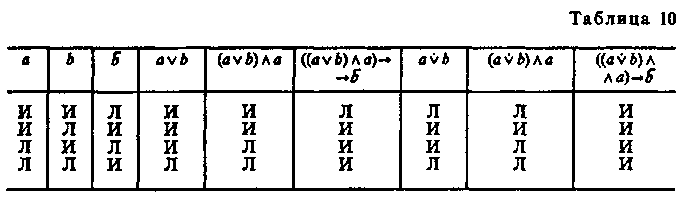Доказательство формул (1) и (3) дано в табл. 10.



Ошибки происходят из-за смешения в этом модусе соедините­льно-разделительного и строго разделительного смысла союза «или». Нельзя, например, рассуждать таким образом:
Учащиеся в контрольной работе по математике допускают или вычислитель­ные ошибки, или ошибки в эквивалентных преобразованиях, или ошибки в приме­нении изученных алгебраических правил.

Учащийся Сидоров допустил в контрольной работе вычислительные ошибки.

_________________________________________________________________________________________

Сидоров не допустил в работе ни ошибок в эквивалентных преобразованиях, ни ошибок в применении изученных алгебраических правил.
Заключение не является истинным суждением, так как Сидо­ров мог допустить все три вида ошибок.

II модус — отрицающе-утверждающий (modus tollendo ponens). Приведем пример.
Минеральные удобрения бывают или азотными, или фосфорными, или калий­ными.

Данное минеральное удобрение не является ни азотным, ни фосфорным.

_____________________________________________________________________

Данное минеральное удобрение является калийным.
Приведем второй пример. Для этого воспользуемся рас­сказом «Пестрая лента» А. Конан Дойла. Шерлок Холмс рас­сказал Уотсону: «Вначале я пришел к совершенно неправильным выводам, мой дорогой Уотсон, — и это доказывает, как опасно опираться на неточные данные. Присутствие цыган, слово «бан­да», сказанное несчастной девушкой, — всего этого было до­статочно, чтобы навести меня на ложный след. Но когда мне стало ясно, что в комнату невозможно проникнуть ни через дверь, ни через окно, что не оттуда грозит опасность обитателю этой комнаты, я сразу понял свою ошибку, и это может послу­жить мне оправданием. Как я уже говорил вам, внимание мое сразу привлекли вентилятор и шнур от звонка, висящий над кроватью. Когда обнаружилось, что звонок фальшивый, а кро­вать прикреплена к полу, у меня сразу зародилось подозрение, что шнур служит лишь мостом, соединяющим вентилятор с кроватью. Мне сразу пришла мысль о змее, а зная, как доктор любит окружать себя всевозможными индийскими тварями, я понял, что, пожалуй, напал на верный след. Именно такому хитрому, жестокому злодею, прожившему много лет на Востоке, могло прийти в голову употребить яд, который нельзя об­наружить химическим путем».

Отрицающе-утверждающий модус (для случая двучленной разделительной посылки) в виде правила вывода в алгебре логи­ки может бытьзаписан следующим образом: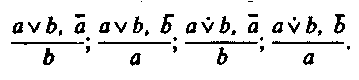

Логический союз «или» здесь может употребляться в двух смыслах: как строгая дизъюнкция (v) и как нестрогая дизъюнк­ция (v), т. е. характер дизъюнкции на необходимость заключе­ния по этому модусу не влияет.

Выводы по этому модусу выражаются четырьмя формулами, которые являются законами логики:

1) 2)
Можно привести относительно новую разновидность струк­туры разделительно-категорического умозаключения, построен­ного по отрицательно-утверждающему модусу. Например, в рас­сказе Агаты Кристи «Двойная улика» мистер Пуаро расследует похищение ряда драгоценностей из коллекции Хардмана (жем­чужины, рубины, изумрудное ожерелье). Подозрение могло ка­саться четверых. Вот их диалог, в котором сформулировано умозаключение:

«— Понимаю, — произнес задумчиво Пуаро. — И вы безого­ворочно ему доверяете?

— У меня не было причин для недоверия.

— Мистер Хардман, кого вы сами подозреваете из этой чет­верки?

— О, мсье Пуаро, что за вопрос! Ведь я вам уже сказал, что это мои друзья. Я ни одного из них не подозреваю или, если вам угодно, — всех в одинаковой мере.

— Не могу с вами согласиться. Я уверен, что вы кого-то из них подозреваете. Это не графиня Росакова, Это не мистер Паркер. Кто же тогда: леди Ранкорн или мистер Джонстон?»

Обязательным условием при выводах по разделительно-кате­горическому умозаключению является соблюдение правила о том, что в разделительной посылке должны быть предусмот­рены все возможные альтернативы, т. е. деление должно быть полным. Это правило для отрицающе-утверждающего модуса обязательно.
Пожар мог произойти или в результате небрежного обращения с огнем, или в результате поджога, или по причине неисправной электропроводки.

Данный пожар не произошел ни в результате небрежного обращения с огнем, ни по причине неисправной электропроводки.

___________________________________________________

Данный пожар произошел в результате поджога.

Заключение не достоверное, а вероятное, так как в первой разделительной посылке перечислены не все возможные причины возникновения пожара (например, в результате взрыва или в ре­зультате загорания от молнии и т. д.).
§ 9. УСЛОВНО-РАЗДЕЛИТЕЛЬНЫЕ (ЛЕММАТИЧЕСКИЕ) УМОЗАКЛЮЧЕНИЯ
Условно-разделительное умозаключение — это такое умоза­ключение, в котором одна посылка состоит из двух или более условных суждений, а другая является разделительным суждени­ем. В зависимости от числа членов в разделительной посылке это умозаключение может быть дилеммой (если разделительная по­сылка содержит два члена), трилеммой (если разделительная посылка содержит три члена) и вообще полилеммой (число раз­делительных членов больше двух).
Формализация дилеммы

Дилеммы бывают двух видов: конструктивные и деструктив­ные; обе формы дилеммы в свою очередь могут быть простыми и сложными.
Простая конструктивная дилемма

Это умозаключение состоит из двух посылок. В первой посыл­ке утверждается, что из двух различных оснований вытекает одно и то же следствие. Во второй посылке, которая является дизъюн­ктивным суждением, утверждается, что одно или другое из этих оснований истинно. В заключении утверждается следствие.

В традиционной формальной логике простую конструктив­ную дилемму обычно представляют в виде следующей схемы:
Если А есть В, то С есть D; если Е есть F, то С есть D.

А есть В или Е есть F.

___________________________________________________

С есть D.
Приведем пример простой конструктивной дилеммы.

В романе В. Шукшина «Я пришел дать вам волю» написано так: «Давай думать, как быть. Две дороги домой: Кумой или Волгой. Обои закрыты. Там и тут надо пробиваться силой. Добром нас никакой дурак не пропустит. А раз такое дело, давай решим: где легче».

Простая конструктивная дилемма представлена в такой форме:
Если плыть Кумой (а), то надо пробиваться силой (Ь);

если плыть Волгой (с), то надо пробиваться силой (b).

Можно плыть Кумой (а) или Волгой (с).

______________________________

Надо пробиваться силой (b).
Выразим суждение «А есть В» переменной а, суждение «С есть D» — переменной b, суждение «Е есть F» — переменной с. Тогда схема простой конструктивной дилеммы выразится в виде следу­ющего правила вывода:

В данном случае формула указанного вида будет такова:



Доказательство тождественной истинности этой формулы мо­жно провести табличным методом. Приведем еще один пример простой конструктивной ди­леммы:
Если я пойду через речку по мосту, меня могут заметить враги;

если я пойду через речку вброд, меня тоже могут заметить враги.

Я могу идти через речку по мосту или вброд.

___________________________________

Меня могут заметить враги.
Сложная конструктивная дилемма

Это умозаключение строится из двух посылок. В первой посылке имеются два основания, из которых вытекают соответ­ственно два следствия; во второй посылке, которая представляет собой дизъюнктивное суждение, утверждается истинность одного или другого основания; в заключении утверждается истинность одного или другого следствия. Сложная конструктивная дилемма отличается от простой конструктивной дилеммы только тем, что оба следствия ее условной посылки различны, а не одинаковы.

Этот вид дилеммы значительно чаще встречается в мышлении людей, в сознании литературных героев, исторических деятелей, поэтому мы приведем пример из художественной литературы.

Т. Тэсс в рассказе «Поединок в море» описывает такую ситу­ацию. Танкер «Ростов» взял около десяти тысяч тонн автомо­бильного бензина и уже готовился в Туапсе к отплытию... Сейчас танкер должен сняться с якоря... Якорь уже вышел из воды... На лапе якоря висит авиабомба, пролежавшая на дне моря двадцать лет. Капитан танкера «Ростов» Александр Котляров думал не только о своем судне, а и о других танкерах, тоже залитых бензином и нефтью, стоящих неподалеку от причалов. «Сколько времени пройдет, пока из Севастополя в Туапсе придут минеры? Бомба может взорваться каждую минуту. Двадцать лет она пролежала под водой, а сейчас может взорваться от любой случайности».

Перед капитаном встала очень сложная дилемма:
Если я оставлю танкер в порту до прибытия минеров, то бомба может

взорваться и повредить много судов; если я уведу танкер в море,

то в случае взрыва пострадает только один танкер.

Я могу оставить танкер в порту до прибытия минеров или увести в море.

__________________________________________________________________________________________

Могут пострадать много судов в порту, или в случае взрыва пострадает только один танкер.
Капитан принимает такое решение: «Немедленно, не дожида­ясь прибытия из Севастополя минеров, уйти из порта в море. Уйти, чтобы обезопасить другие суда, отплыть на такое расстояние, чтобы в случае взрыва опасность грозила только одному его танкеру. Уйти в море и там утопить бомбу». Танкер ушел из порта, и со второй попытки бомбу удалось утопить в море, а танкер не пострадал.

Так как дилемма означает сложный выбор из двух альтер­натив одной, причем обе они нежелательны для субъекта (такая ситуация характеризуется выражением «из двух зол выбирать наименьшее»), то в древности о дилемме говорили: «Посадить на рога дилеммы». В нашей речи встречается выражение: «Передо мной стоит дилемма» (т. е. сложный выбор).

Схема сложной конструктивной дилеммы:

Формула:



Данная формула выражает закон логики, что можно доказать табличным способом.

Простая деструктивная дилемма

В этом умозаключении первая (условная) посылка указывает на то, что из одного и того же основания вытекают два различных следствия; вторая посылка представляет собой дизъюнкцию отри­цаний обоих этих следствий; в заключении отрицается основание.

Пример:
Если человек болен сыпным тифом, то на 4—6-й день болезни у него будет высокая температура и появится сыпь.

У больного нет высокой температуры или нет сыпи.

____________________________________________

Этот человек не болен сыпным тифом.
Схема этой дилеммы:

Этой схеме соответствует формула



Простая деструктивная дилемма может быть построена и по другой схеме:

Этой схеме соответствует формула

Сложная деструктивная дилемма

Дилемма такого вида содержит одну посылку, состоящую из двух условных суждений с разными основаниями и разными следствиями; вторая посылка есть дизъюнкция отрицаний обоих следствий; заключение является дизъюнкцией отрицаний обоих оснований. В форме, обычной для традиционной логики, слож­ную деструктивную дилемму можно представить в виде следу­ющей схемы:

Если А есть В, то С есть D; если Е есть F, то К есть М.

С не есть Dили К не есть М.

___________________________

А не есть В или Е не есть F.
Примером рассуждения по форме сложной деструктивной дилем­мы может быть следующий вывод:
Если Петров честен, то, не выполнив задания сегодня, он признается в этом, а если Петров добросовестен, то он выполнит задание к следующему разу.

Но Петров не признался в том, что он сегодня не выполнилзадание, или не сделал его к следующему разу.

__________________________________________________

Петров не честен или не добросовестен⁴.
Схема сложной деструктивной дилеммы такая:

Этой схеме соответствует формула которая является законом логики.


В предыдущих схемах, соответствующих четырем видам ди­леммы, во второй (разделительной) посылке союз «или» взят в соединительно-разделительном смысле, т. е. взята нестрогая дизъюнкция (v). Будут ли формулы алгебры логики, соответст­вующие дилеммам (четыре вида), тождественно-истинными, если союз «или» употребляется в строго разделительном смысле, т. е. если взята строгая дизъюнкция (v)? Являются ли законами логики следующие формулы:

1) 2)

3) 4)

(Так как конъюнкция связывает «теснее», чем импликация, то скобки можно опустить.)

Автором этой книги показано⁵, что независимо от того, какая дизъюнкция (строгая или нестрогая) входит в соответст­вующие формулы, простым дилеммам (конструктивной и дест­руктивной) соответствуют законы логики. Сложным дилеммам (и конструктивной, и деструктивной) соответствуют законы логики лишь в том случае, если, союз «или» рассматривается как нестрогая дизъюнкция. Но в ходе рассуждения, построенного в форме сложной дилеммы, человек употребляет именно стро­гую дизъюнкцию, ибо перед ним две взаимоисключающие возможности (причем обе они нежелательны). Это несоответст­вие возникло из-за отсутствия полного совпадения смысла союза «если... то» и смысла материальной импликации (в двузначной логике).

Некоторые логики под дилеммой понимают такое умозак­лючение:
Если А есть В, то С есть D; если Е есть F, то GестьH.

Но С не есть Dи Gне есть H.

___________________________________

Следовательно, А не есть В и Е не есть F.
Пример:

Если бы я был богат, то я бы купил автомобиль.

Если бы я был бесчестен, то я украл бы таковой.

Но я его не купил и не украду.

_______________________________

Я не богат и не бесчестен.
Но здесь вторая посылка и заключение являются конъюнктив­ными, а не дизъюнктивными суждениями (как это должно быть по правилам построения дилеммы), поэтому приведенное выше умозаключение не является дилеммой, так как в нем нет раз­делительной посылки, характерной для дилеммы. Это умозак­лючение есть простая сумма двух условно-категорических умоза­ключений, построенных по правилу modus tollens, который дает истинное заключение. Формула modus tollens такая:


1. Если бы я был богат, то я бы купил автомобиль.

Я не куплю автомобиль.

________________

Я не богат.
2. Если бы я был бесчестен, то я украл бы автомобиль.

Я не украду автомобиль.

_________________

Я не бесчестен.
Итак, перед нами условно-конъюнктивное, а не условно-дизъюн­ктивное (лемматическое) умозаключение.
Трилемма

Трилеммы, так же как и дилеммы, могут быть конструктив­ными и деструктивными; каждая из этих форм в свою очередь может быть простой или сложной. Простая конструктивная трилемма состоит из двух посылок и заключения. В первой посылке констатируется то, что из трех различных оснований вытекает одно и то же следствие; вторая посылка представляет собой дизъюнкцию этих трех оснований; в заключении утвержда­ется следствие.
Если у больного грипп, то рекомендуется обратиться к врачу; если у больного

острое респираторное заболевание, то рекомендуется обратиться к врачу; если у больного ангина, то рекомендуется обратиться к врачу.

У данного больного или грипп, или острое респираторное заболевание, или ангина.

__________________________________________________

Данному больному рекомендуется обратиться к врачу.
В сложной конструктивной трилемме первая посылка состоит из трех различных оснований и трех различных вытекающих из них следствий, т. е. содержит три условных суждения. Вторая посылка является дизъюнктивным суждением, в котором утверж­дается (по крайней мере) одно из трех оснований. В заключении утверждается (по крайней мере) одно из трех следствий.

Приведем пример сложной конструктивной трилеммы. В не­которых сказках говорится о надписях на перекрестках трех дорог, которые содержат, например, такого рода трилемму:
Кто поедет прямо, будет в холоде и голоде; кто поедет направо, тот сам останется цел, а конь будет убит; кто поедет налево, тот сам будет убит, а конь останется цел.

Человек может поехать либо прямо, либо направо, либо налево.

_____________________________________________________________

Он или будет в холоде и голоде, или сам останется цел, а конь будет убит, или сам будет убит, а конь останется цел.
Приведем еще пример трилеммы.
В своих воспоминаниях о Великой Отечественной войне Л. И. Баркович пишет об истории Ладожской дороги. Ладожс­кая дорога, Дорога жизни, была фронтом. Направляясь в Ленин-

град по Ладожскому озеру, Иван Игнатьевич Баркович, будучи шофером грузовой машины, взял с собой сына Леонида, так как вторую машину — полуторку вести было некому. В автоколонне сын двигался за машиной отца. Дорога была опасна. Враг дер­жал ее под огнем, лед расходился, образуя просветы. Вдруг машина отца остановилась — оказалось, кончился бензин.

Леонид Баркович рассуждает:

«У моей машины горючее тоже было на исходе. Переливать половину оставшегося бензина в бак отцовского «газика» было глупо — горючее могло кончиться раньше, чем мы добрались бы до берега.

Поехать вперед, сообщить, что тут стоит машина? Но по­мощь может прийти поздно...

Взять на буксир его машину — лед мог не выдержать».

Леонид принял решение: «Давай трос! На буксире у меня войдешь!» Добрались благополучно.

Деструктивные трилеммы, так же как и деструктивные ди­леммы, бывают простые и сложные. Структура их аналогична структуре дилеммы, только предусматриваются не две, а три возможные альтернативы.

Приведем пример простой деструктивной трилеммы.
Если в ближайшее время погода ухудшится» то у него будут болеть суставы, повысится артериальное давление и будет ломить поясница.

Известно, что у него или не болят суставы, или не повысилось артериаль­ное давление, или не ломит поясница.

__________________________________________

В ближайшее время погода не ухудшится.
В математике структура трилеммы используется тогда, когда возникают три возможных варианта решения задачи, доказатель­ства теоремы и предстоит выбор одного из них.
Сокращенные условные, разделительные и условно-разделительные умозаключения

Категорический силлогизм в мышлении часто употребляется в сокращенной форме — в форме энтимемы. Сокращенными мо­гут быть не только простые категорические силлогизмы, но и условные, и разделительные, и условно-разделительные умоза­ключения, в которых может быть пропущена либо одна из посы­лок, либо заключение. Рассмотрим типы таких сокращенных умозаключений.

1. В умозаключении заключение в явном виде может не формулироваться. «Если данное тело — металл, то оно при на­ревании расширяется. Данное тело — металл». Заключение Данное тело при нагревании расширяется» не формулируетсяв явном виде, а просто подразумевается в этом условно-катего­рическом умозаключении.

В приводимом ниже разделительно-категорическом умозак­лючении также пропущено заключение. «Многоугольники делят­ся на правильные и неправильные. Данный многоугольник непра­вильный». Заключение «Данный многоугольник не является пра­вильным» опущено; оно легко может быть восстановлено.

В дилеммах и трилеммах заключение также может явно не формулироваться, а подразумеваться. Например, в приведенной ниже сложной деструктивной дилемме заключение явно не при­сутствует:

«Если соблюдать правила хранения зерна, то не произойдет его самозагорания, а если организовать хорошую охрану зернохранилища, то не произойдет умышленного поджога. Данный пожар произошел либо от самозагорания зерна, либо от умыш­ленного поджога». Заключение — «В данном зернохранилище либо не соблюдаются правила хранения зерна, либо не налажена охрана» — подразумевается, а не высказывается в явной форме.

2. В умозаключении пропущена одна из посылок. В умозак­лючениях может быть пропущена первая посылка; она может подразумеваться, если выражает известное положение, теорему, закон и т. д.

В условно-категорическом умозаключении «Сумма цифр дан­ного числа делится на 3, следовательно, данное число делится на 3» опущена первая посылка, формулирующая известную матема­тическую закономерность: «Если сумма цифр данного числа делится на 3, то все число делится на 3».

В приводимом ниже разделительно-категорическом умозак­лючении также пропущена первая посылка: «Существительное в русском языке может быть женского, мужского или среднего рода», а все умозаключение сокращенно формулируется так: «Данное существительное русского языка не является сущест­вительным ни женского рода, ни среднего рода. Следовательно, данное существительное мужского рода».

В приведенном ниже примере сложной конструктивной дилем­мы: «Если я пойду через болото, то могу попасть в трясину, а если я пойду в обход, то не успею вовремя доставить донесение. Следовательно, я могу попасть в трясину или не успею вовремя доставить донесение» — вторая посылка не формулируется, а лишь подразумевается: «Я могу идти через болото или в обход».

Можно было бы привести и другие примеры сокращенных умозаключений: чисто условных, условно-категорических, чисто разделительных, разделительно-категорических, условно-разде­лительных (дилемм, трилемм) с пропущенной первой или второй посылкой, — но предоставляем это самостоятельно сделать чи­тателю.

Итак, рассмотренные нами прямые выводы, такие, как чисто условные, чисто разделительные, условно-категорические, разде­лительно-категорические и условно-разделительные (лемматические) умозаключения, сформулированные полностью и сокра­щенные (т. е. в которых пропущена либо одна из посылок, либо заключение), широко используются в процессе научного и обы­денного мышления, в процессе обучения в школе и в вузе. Поэто­му знание правил построения этих видов умозаключений пре­достережет от логических ошибок в мышлении, поможет до­казательнее, аргументированнее строить свои рассуждения и сде­лать более эффективным обучение учащихся и студентов.

Прямые выводы кроме рассмотренных выше форм включают и такие виды:

1. Простая контрапозиция.

Правило простой контрапозиции имеет следующий вид:

Это правило читается так: «Если а имплицирует b, то отрица­ние bимплицирует отрицание а». Здесь а и b— переменные, обозначающие произвольные высказывания, или пропозицио­нальные переменные.

Пример:

1. Если данный треугольник равносторонний, то он равноугольный.

____________________________________________________________________

Если данный треугольник не равноугольный, то он не равносторонний.
2. Если это вещество фосфор, то оно непосредственно с водородом не сое­диняется.

_____________________________________________________________________________________

Если вещество непосредственно с водородом соединяется, то это вещество не является фосфором.
Заметим, что в логике высказываний

Формуланазывается законом простой контрапозиции.

2. Сложная контрапозиция.

— правило сложной контрапозиции.

Пример рассуждения по правилу сложной контрапозиции:
Если у меня будут деньги и я буду здорова, то я поеду домой на каникулы.

________________________________________________________________________

Если у меня были деньги и я не поехала на каникулы домой, то, следовательно, а не была здорова.
3. Правило импортации (конъюнктивного объединения условий). П. С. Новиков называет его правилом соединения посылок:

Это правило читается так: «Если а имплицирует, что bимп­лицирует с, то а и bимплицируют с».

В. А. Сухомлинский писал: «Если учитель стал другом ребен­ка, если эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, в сердце ребенка никогда не появится зло». На основании правила соединения посылок (пра­вила конъюнктивного объединения условий) мы можем это вы­сказывание В. А. Сухомлинского записать иначе, но оно будет эквивалентно прежнему его высказыванию. Заключение: «Если учитель стал другом ребенка и эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, то в сердце ребенка никогда не появится зло».

4. Правило экспортации (разъединения условий):

Это правило читается так: «Если а и bимплицируют с, то а имплицирует, что bимплицирует с. Правило это обратно предыдущему. Поэтому в качестве иллюстрации можно взять те же мысли В. А. Сухомлинского, только сначала прочитать наше полученное заключение, из которого можно прийти к высказыва­нию самого В. А. Сухомлинского.