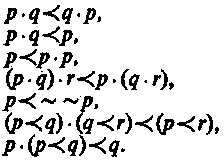|
|
Логика. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
§ 4. ИНТУИЦИОНИСТСКАЯ ЛОГИКА
Интуиционистская логика построена в связи с развитием интуиционистской математики. Интуиционистская школа основана в 1907 г. голландским математиком и логиком Л. Брауэром (1881—1966)35, но некоторые ее идеи выдвигались и ранее.
Интуиционизм — философское направление в математике и логике, отказывающееся от использования абстракции актуальной бесконечности, отвергающее логику как науку, предшествующую математике, и рассматривающее интуитивную ясность и убедительность («интуицию») как последнюю основу математики и логики. Интуиционисты свою интуиционистскую математику строят с помощью финитных (конечных) средств на основе системы натуральных чисел, которая считается известной из интуиции. Интуиционизм включает в себя две стороны — философскую и математическую.
Математическое содержание интуиционизма изложено в ряде работ математиков. Ведущие представители отечественной школы конструктивной математики отмечают положительное значение некоторых математических идей интуиционистов.
В целом конструктивная математика существевно отличается от интуиционистской. Советский математик-конструктивист А. А. Марков (1903—1979) пишет о том, что конструктивное направление имеет точки соприкосновения с так называемой интуиционистской математикой. Конструктивисты сходятся с интуиционистами в понимании дизъюнкции и в силу этого признают правильной данную Брауэром критику закона исключенного третьего. Вместе с тем конструктивисты считают неприемлемыми методологические основы интуиционизма.
В этом высказывании ясно разделены две стороны интуиционизма — математическая и философская. Если первая сторона имеет рациональную часть (в этой связи предпочтительнее говорить об интуиционистской математике или интуиционистской логике, а не об интуиционизме), то вторая сторона интуиционизма (его методологические, идеалистические, философские основы) совершенно неприемлема.
Брауэр считал, что чистая математика представляет собой свободное творение разума и не имеет никакого отношения к опытным фактам. У интуиционистов единственным источником математики оказывается интуиция, а критерием приемлемости математических понятий и выводов является «интуитивная ясность». Но интуиционист Гейтинг вынужден признаться в том, что понятие интуитивной ясности в математике само не является интуитивно ясным; можно даже построить нисходящую шкалу степеней очевидности.
Основой происхождения математики в конечном итоге является не какая-то «интуитивная ясность» — продукт сознания человека, а отражение пространственных форм и количественных отношений действительного мира. Гейтинг, как и Брауэр, в гносеологии тоже субъективный идеалист. Он утверждает, что для математической мысли характерно, что она не выражает истину о внешнем мире, а связана исключительно с умственными построениями36.
Еще в 1936 г. советский математик А. Н. Колмогоров подверг критике субъективно-идеалистические основы интуиционизма, заявив, что невозможно согласиться с интуиционистами, когда они говорят, что математические объекты являются продуктом конструктивной деятельности нашего духа, ибо математические объекты являются абстракциями реально существующих форм независимой от нашего духа действительности. Интуиционисты не признают человеческую практику и опыт источником формирования математических понятий, методов математических построений и методов доказательств.
Особенности интуиционистской логики вытекают из характерных признаков интуиционистской математики.
В современной классической математике часто прибегают к косвенным доказательствам. Но их почти невозможно ввести в интуиционистской математике и логике, так как там не признаются закон исключенного третьего и законкоторые участвуют в косвенных доказательствах.
Закон исключенного третьего для бесконечных множеств в интуиционистской логике не проходит потому, что знак отрицания) требует общего метода для решения любой проблемы или, более явно, общего метода, который по произвольному высказыванию р позволил бы получать либо доказательство р, либо доказательство отрицания р. Гейтинг считает, что так как интуиционисты не располагают таким методом, то они и не вправе утверждать принцип исключенного третьего. Покажем это на таком примере. Возьмем утверждение: «Всякое целое число, большее единицы, либо простое, либо сумма двух простых, либо сумма трех простых». Неизвестно, так это или нет, хотя в рассмотренных случаях, которых конечное число, это так. Существует ли число, которое не удовлетворяет этому требованию? Мы не можем указать такое число и не можем вывести противоречие из допущения его существования.»
Эта знаменитая проблема Гольдбаха (X. Гольдбах — математик) была поставлена им в 1742 г. и не поддавалась решению около 200 лет. Гольдбах высказал предположение, что всякое целое число, большее или равное шести, может быть представлено в виде суммы трех простых чисел. Для нечетных чисел она была положительно решена только в 1937 г. советским математиком — академиком И. М. Виноградовым; все достаточно большие нечетные числа представимы в виде суммы трех простых чисел. Это одно из крупнейших достижений современной математики. Но закон непротиворечия представители как интуиционистской, так и конструктивной логик считают неограниченно применимым.
Брауэр первый наметил контуры новой логики. Идеи Брауэра формализовал Гейтинг, в 1930 г. построивший интуиционистское исчисление предложений с использованием импликации, конъюнкции, дизъюнкции и отрицания на основе 11 аксиом и двух правил вывода — модуса поненс (modus ponens) и правила подстановки. Гейтинг утверждает, что, хотя основные различия между классической и интуиционистской логиками касаются свойств отрицания, эти логики не совсем совпадают и в формулах без отрицания. Гейтинг отличает математическое отрицание от фактического: первое выражается в форме конструктивного построения (выполнения) определенного действия, а второе говорит о невыполнении действия (а «невыполнение» чего-либо не является конструктивным действием). Интуиционистская логика имеет дело только с математическими суждениями и лишь с математическим отрицанием, которое определяется через понятие противоречия, а понятие противоречия интуиционисты считают первоначальным, выражающимся или приводящимся в форме 1 = 2, Фактическое отрицание не связано с понятием противоречия.
Проблемами интуиционистской логики в нашей стране занимаются К. Н. Суханов, М. И. Панов, А. Л, Никифоров и др.
§ 5. КОНСТРУКТИВНЫЕ ЛОГИКИ
Конструктивная логика, отличная от логики классической, своим рождением обязана конструктивной математике. Конструктивная математика может быть кратко охарактеризована как наука о конструктивных процессах и нашей способности их осуществлять. В результате конструктивного процесса возникает конструктивный объект, т. е. такой объект, который задается эффективным (точным и вполне понятным) способом построения (алгоритмом)37.
Конструктивное направление (в математике и логике) ограничивает исследование конструктивными объектами и проводит его в рамках абстракции потенциальной осуществимости (реализуемости), т. е. игнорирует практическое ограничение наших возможностей построений в пространстве, времени, материале.
Между идеями конструктивной логики советских исследователей и некоторыми идеями интуиционистской логики (например, в понимании дизъюнкции, в отказе от закона исключенного третьего) имеются точки соприкосновения.
Однако конструктивная и интуиционистская логики имеют существенные отличия.
1. Различные объекты исследования. В основу конструктивной логики, которая является логикой конструктивной математики, положена абстракция потенциальной осуществимости, а в качестве объектов исследования допускаются лишь конструктивные объекты (слова в определенном алфавите).
В основу интуиционистской логики, являющейся логикой интуиционистской математики, положена идея «свободно становящейся последовательности» (т. е. последовательности, строящейся не по алгоритму), которую интуиционисты считают интуитивно ясной.
2. Обоснование интуиционистской математики и логики дается с помощью идеалистически истолкованной интуиции, а обоснование конструктивной математики и логики дается на базе научного математического понятия алгоритма (например, нормального алгоритма А. А. Маркова) или эквивалентного ему понятия рекурсивной функции.
3. Различные методологические основы. Методологической основой конструктивного направления в математике отечественные исследователи считают положения материализма, с позиций которого критерием истинности познания (в том числе и научного) является практика. Это положение сохраняет свою силу и для таких наук, как логика и математика, хотя здесь практика входит в процесс познания лишь опосредованно, в конечном счете.
Интуиционисты же, оставаясь в рамках субъективно-идеалистической философии, считают источником формирования математических понятий и методов не человеческую практику, а первоначальную «интуицию», а критерием истинности в математике — «интуитивную ясность».
4. Различные интерпретации**. А. Н. Колмогоров рассматривал интуиционистскую логику как исчисление задач. А. А. Марков определял логические связки конструктивной логики как прилагаемые к потенциально осуществляемым конструктивным процессам (действиям).
Интуиционистская логика Л. Брауэра и А. Гейтинга интерпретируется ими как исчисление предложений (высказываний), причем область высказываний у них ограничивается математическими предложениями.
5. Отличие ряда логических средств. Отечественные представители узко-конструктивной логики признают в качестве принципа: если имеется алгоритмический процесс и удалось опровергнуть, что он продолжается бесконечно, то, следовательно, процесс закончится. Некоторые из представителей конструктивной логики доказывают его в уточненной форме.
Представители интуиционистской логики не признают этот принцип.
Конструктивные исчисления высказываний В. И. Гливенко и А. Н. Колмогорова
Первыми представителями конструктивной логики были наши отечественные математики — А. Н. Колмогоров (1903— 1987) и В. И. Гливенко (1897—1940). Первое исчисление, не содержащее закона исключенного третьего, было предложено в 1925 г. А. Н. Колмогоровым в связи с его критикой концепции Л. Брауэра, а в дальнейшем развито В. И. Гливенко. Позже было опубликовано исчисление Гейтинга, которое Колмогоров интерпретировал как исчисление задач, что легло в основу содержательного истолкования исчислений, не пользующихся законом исключенного третьего, а это, в свою очередь, стало основой всех дальнейших, подлинно научных исследований таких исчислений.
С помощью введения понятий «псевдоистинность» (двойное отрицание суждения) и «псевдоматематика» («математика псевдоистинности») Колмогоров доказал, что всякий вывод, полученный с помощью закона исключенного третьего, верен, если вместо каждого суждения, входящего в его формулировку, поставить суждение, утверждающее его двойное отрицание. Тем самым он показал, что в «математике псевдоистинности» возможно применение принципа исключенного третьего.
Колмогоров различает две логики суждений —общую и частную. Различие между ними в одной аксиоме А-> А, которая имеется лишь среди аксиом частной логики. Интересна взаимосвязь соотношения содержания и областей применения этих логик: содержание частной логики суждений богаче, чем обшей, так как частная логика дополнительно включает аксиомуно область применения ее уже. Из системы частной логики можно вывести все формулы традиционной логики суждений.
Какова же область применения частной логики суждений? Все ее формулы верны для суждений типа А', в том числе для всех финитных и для всех отрицательных суждений, т. е. область применимости ее совпадает с областью применимости формулы двойного отрицания(Символами А', В' ... обозначены произвольные суждения, для которых из двойного отрицания следует само суждение.)
Конструктивная логика А. А. Маркова
Проблема конструктивного понимания логических связок, в частности отрицания и импликации, требует применения в логике специальных точных формальных языков. В основе конструктивной математической логики А. А. Маркова лежит идея ступенчатого построения формальных языков. Сначала вводится формальный язык Яо , в котором предложения выражаются по
определенным правилам в виде формул; в нем имеется определение смысла выражения этого языка, т. е. семантика. Правила вывода позволяют, исходя из верных предложений, всегда получать верные предложения.
В конструктивной математике формулируются теоремы существования, утверждающие, что существует объект, удовлетворяющий таким-то требованиям. Под этим подразумевается, что построение такого объекта потенциально осуществимо, т. е. мы владеем способом его построения. Это конструктивное понимание высказываний о существовании отличается от классического. В конструктивной математике и логике иной является и трактовка дизъюнкции, которая понимается как осуществимость указания ее верного члена. «Осуществимость» означает потенциальную осуществимость конструктивного процесса, дающего в результате один из членов дизъюнкции, который должен быть истинным. Классическое же понимание дизъюнкции не предполагает нахождения ее истинного члена.
Новое понимание логических связок требует новой логики. Мы считаем утверждение А. А. Маркова о неединственности логики верным и весьма глубоким: «В самой идее неединственности логики, разумеется, нет ничего удивительного. В самом деле, с какой стати все наши рассуждения, о чем бы мы ни рассуждали, должны управляться одними и теми же законами? Для этого нет никаких оснований. Удивительным, наоборот, было бы, если бы логика была единственна»39.
В конструктивную математическую логику А. А. Марков вводит понятие «разрешимое высказывание» и связанное с ним понятие «прямое отрицание». В логике А. А. Маркова имеется и другой вид отрицания — усиленное отрицание, относящееся к так называемым полуразрешимым высказываниям.
Кроме материальной и усиленной импликации, при установлении истинности которых приходится заботиться об истинности посылки и заключения, А. А. Марков вводит дедуктивную импликацию, определяемую по другому принципу. Дедуктивная импликация «если А, то В» выражает возможность выведения В из А по фиксированным правилам, каждое из которых в применении к верным формулам даст верные формулы. Всякое высказывание, выводимое из истинного высказывания, будет истинным.
Через дедуктивную импликацию А. А. Марков определяет редукционное отрицание (reductio ad absurdum). Редукционное отрицание высказывания А (сформулированного на данном языке) понимается как дедуктивная импликация «если А, то Л», где через Л обозначен абсурд. Это определение отрицания соответствует обычной практике рассуждений математика: математик отрицает ту посылку, из которой вытекает абсурд. Для установления истинности редукционного отрицания высказывания не требуется вникать в смысл этого высказывания. Высказывание, для которого установлена истинность редукционного отрицания, не может быть истинным.
Эти три различных понимания отрицания не вступают в конфликт друг с другом, они согласованы, что, по мнению А. А. Маркова, даст возможность объединить все эти понимания отрицания.
Показательно такое обстоятельство: А. А. Марков строит свои конструктивные логические системы для обоснования конструктивной математики таким образом, что у него получается не одна законченная система, а целая иерархия систем. Это система языков Я0, Я1 Я2, Я3, Я4, Я5, ..., Я N (где N — натуральное число) и объемлющего их языка Яωпосле Яωстроится язык Яω`.
Итак, мы склонны думать, что развивающуюся конструктивную логику и математику невозможно вместить в одно формальное исчисление, для этого нужна система, состоящая из целой иерархии систем, в которой будет иерархия отрицаний.
Проблемами конструктивной логики и теории алгоритмов занимается российский математик Н. М. Нагорный и др.
§ 6. МОДАЛЬНЫЕ ЛОГИКИ
В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т. е. такие, в которых не установлен характер связи между субъектом и предикатом. Например: «Морская вода — соленая» или «Дождь то начинал хлестать теплыми крупными каплями, то переставал».В модальных суждениях раскрывается характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном модальном суждении. Например: «Необходимо соблюдать правила уличного движения» или «Если будет дуть попутный ветер, то, возможно, мы приплывем в гавань до наступления темноты».
Модальными являются суждения, которые включают модальные операторы (модальные понятия), т. е. слова «необходимо», «возможно», «невозможно», «случайно», «запрещено», «хорошо» и многие другие (см. гл. Ш, § 6 «Деление суждений по модальности»). Модальные суждения рассматриваются в специальном направлении современной формальной логики — в модальной логике.
Изучение модальных суждений имеет длительную и многогранную историю. Мы отметим лишь некоторые из ее аспектов. Модальности в логику были введены Аристотелем. Термин «возможность», по Аристотелю, имеет различный смысл. Возможным он называет и то, что необходимо, и то, что не необходимо, и то, что возможно. Исходя из понимания модальности «возможность», Аристотель писал о неприменимости закона исключенного третьего к будущим единичным событиям.
Наряду с категорическим силлогизмом Аристотель исследует и модальный силлогизм, у которого одна или обе посылки и заключение являются модальными суждениями. Я. Лукасевич в книге «Аристотелевская силлогистика с точки зрения современной формальной логики» две главы посвящает аристотелевой модальной логике предложений и модальной силлогистике Аристотеля40. Аристотель рассматривает модальную силлогистику по образцу своей ассерторической силлогистики: силлогизмы подразделяются на фигуры и модусы, неправильные модусы отбрасываются с помощью их интерпретации на конкретных терминах.
Согласно Аристотелю, случайность есть то, что не необходимо и не невозможно, т. е. р — случайно означает то же самое, что и р — не необходимо и р — не невозможно, но Лукасевич отмечает, что аристотелевская теория случайных силлогизмов полна серьезных ошибок41. Итог Лукасевича такой: пропозициональная модальная логика Аристотеля имеет огромное значение для философии; в работах Аристотеля можно найти все элементы, необходимые для построения полной системы модальной логики; однако Аристотель исходил из двузначной логики42, в то время как модальная логика не может быть двузначной. К идее многозначной логики Аристотель подошел вплотную, рассуждая о «будущем морском сражении». Следуя Аристотелю, Лукасевич в 1920 г. построил первую многозначную (трехзначную) логику. Так осуществляется связь модальных и многозначных логик.
Значительное внимание разработке модальных категорий уделяли философы в Древней Греции и особенно Диодор Крон, рассматривавший модальности в связи с введенной им временной переменной. В средние века модальным категориям также уделялось большое внимание. В XIX в. категорию вероятности разрабатывали Дж. Буль и П. С. Порецкий.
Возникновение модальной логики как системы датируется 1918 годом, когда американский логик и философ Кларенс Ирвинг Льюис (1888—1964) в работе «A Survey of Symbolic Logic» сформулировал модальное исчисление, названное им впоследствии 53.
В книге «Symbolic logic», написанной им совместно с К. Лэнгфордом в 1932 г., он сформулировал еще пять модальных логических систем, связанных с 53 и между собой. Это системы 51, S2, 54, 55, S6.
Приведем описание модальной системы SI43
I. Исходные символы. 1) р, q, rи т. д. — пропозициональные переменные; 2) р — отрицание р;3)— конъюнкция р и q; 4)— строгая импликация льюисовской системы; 5) —
модальный оператор возможности (возможно р); 6) p=q— строгая эквивалентность, p=qравносильно
П. Аксиомы системы S1:
1) 2) 3) 4) 5) 6) 7)
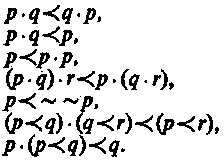
Аксиома 5 может быть выведена из остальных, как было показано позднее. Так как конъюнкция связывает «сильнее», чем импликация, то скобки можно опустить или заменить их точками, как это сделано у Льюиса.
III. Правила вывода S1.
1. Правило подстановки. Любые два эквивалентных друг другу выражения взаимозаменимы.
2. Любая правильно построенная формула может быть подставлена вместо р, или q, или rи т. д. в любом выражении.
3. Если выводимо р и выводимо q, то выводимо
4. Если выводимо р и выводимото выводимоq.
Льюис построил модальную пропозициональную логику S1 в виде расширения немодального (ассерторического) пропозиционального исчисления (сокращенно АПИ). При этом основные черты 51 и других его исчислений были скопированы с формализованной логической системы Principia Mathematica Рассела и Уайтхеда, сформулированы с помощью понятий, только терминологически отличающихся от понятий, использованных в Principia Mathematica. Кроме Рассела и Уайтхеда идеи классической логики развивали многие современные математические логики, например американский логик и математик С. Клини44. Исчисления Льюиса построены аксиоматически по образцу Principia, по аналогии с Principia Льюис доказывает рад специфических теорем.
В классической двузначной логике логическое следование отождествляется с материальной импликацией, допускаются такие формы вывода: 1)т. е. истинное суждение следует из любого суждения («истина следует откуда угодно») и 2)т. е. из ложного суждения следует любое суждение («из лжи следует все, что угодно»). Это противоречит нашему содержательному, практическому пониманию логического следования, поэтому данные формулы, а также и некоторые другие, и соответствующие им принципы логического следования называются парадоксами материальной импликации.
Льюис создал свои новые системы с целью избежать этих парадоксов и ввести новую импликацию, названную им «строгой импликацией», такую, чтобы логическое следование представлялось не чисто формально, а по смыслу (содержательно) и новая импликация была бы ближе к союзу естественного языка «если, то». В строгой импликации Льюисаневозможно утверждать антецедент, т. е. р, и отрицать консеквент, т. е. q45.
В системах Льюиса были устранены парадоксы материальной импликации, т. е. формулы 1) и 2) стали невыводимыми, но появились парадоксы строгой импликации. К ним относятся, например, такие формулы: 3) 4)
Итак, отождествлять строгую импликацию Льюиса со следованием нельзя.
С целью исключить парадоксы строгой импликации Льюиса немецкий математик и логик Ф. В. Аккерман (1896—1962) построил свою систему модальной логики. Он ввел так называемую сильную импликацию, которая не тождественна строгой импликации Льюиса, и модальные операторы Аккермана и Льюиса также не являются тождественными. Аккерман все логические термины и модальные операторы определяет через сильную импликацию так: NAравносильно МА равносильно Здесь А — любая правильно построенная формула системы Аккермана: N — оператор необходимости; М — оператор возможности;— отрицание А; знакобозначает сильную импликацию. Знак— логическая постоянная, обозначающая «абсурдно». Эта постоянная в свою очередь определяется так: где & обозначает конъюнкцию. И последняя формула читается так: из противоречия, т. е. А и не-А, следует абсурд. В системе Аккермана не выводятся формулы, структурно подобные парадоксам, ни материальной импликации, ни строгой импликации.
Системы Льюиса и Аккермана являются бесконечнозначными. В отличие от этих систем первоначально построенные системы Лукасевича являются конечнозначными: одна — трехзначная (1920), другая — четырехзначная (1953). В четырехзначной системе Лукасевича46 также обнаружены парадоксы. Главный из них состоит в том, что ни одно аподиктическое предложение не истинно, т. е. ни одно суждение вида Lot(где Lобозначает необходимость, а α — любая формула) не является истинным. Это означало бы, что необходимых суждений нет, т. е. модальный оператор «необходимо» упраздняется. Лукасевич пишет: «Любое аподиктическое предложение должно быть отброшено»47. Сам Лукасевич считает это достоинствοм своей системы, а понятие «необходимость» — псевдопонятием. С такой точкой зрения, конечно, согласиться нельзя.
Интерпретации модальных логик различны. Известный австрийский философ и логик Р. Карнап (1891—1970) пытался интерпретировать модальные понятия (операторы) с помощью так называемой теории «возможных миров», в которой допускается наличие множества «миров», один из которых — действительный, реальный мир, а остальные — возможные миры. Необходимым объявляется то, что существует во всех мирах, возможным — то, что существует хотя бы в одном.
Р. Карнап в 1946 г., используя понятие «описание состояния», предложил интерпретацию модальных операторов, в основе которой лежала идея различия возможного и действительного миров.
В ином направлении шел финский логик Я. Хинтикка. Критически переосмыслив введенное Карнапом понятие «описание состояния», он разрабатывал технику «модальных множеств», т. е. миров (1957), — оригинальную семантическую концепцию возможных миров. Разработка семантики возможных миров для модальных логик продолжается.
Разнообразными проблемами модальной логики занимается американский логик Р. Фейс48.
В настоящее время разработаны многие виды модальностей (см. табл. 7).
Теорией модальных логик и построением новых модальных логических систем в нашей стране активно занимаются логики А. А. Ивин49, Я. А. Слинин50, О. Ф. Серебряников, В. Т. Павлов и др.
|
|
|
 Скачать 2.39 Mb.
Скачать 2.39 Mb.