Логика. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
 Скачать 2.39 Mb. Скачать 2.39 Mb.
|
|
§ 2. ПОНЯТИЕ О ЛОГИЧЕСКОЙ ФОРМЕ И ЛОГИЧЕСКОМ ЗАКОНЕ. ОСНОВНЫЕ ЭТАПЫ РАЗВИТИЯ ЛОГИКИ И ЕЕ ЗНАЧЕНИЕ В ПОЗНАНИИ Формальная логика — наука о законах и формах правильного мышления. В. С. Меськов пишет: «... предметом науки логики являются рассуждения, а сама она есть наука о рассуждениях. Задачей логики как науки является установление законов и правил, которым подчиняются рассуждения»3. Рассуждения облекаются в логическую форму и строятся в соответствии с логическими законами. Выясним, что понимается под логической формой и логическим законом. Понятие логической формы Логической формой конкретной мысли является строение этой мысли, т. е. способ связи ее составных частей. В логических формах отражается не вся полнота содержания мира, существующего вне нас, а его общие структурные связи, которые необходимо воплощаются и в структуре наших мыслей. Понятия, суждения, умозаключения имеют свои специфические формы (структуры). Структуру мысли, т. е. ее логическую форму, можно выразить при помощи символов. Выявим структуру (логическую форму) в трех следующих суждениях: «Все караси — рыбы», «Все люди смертны», «Все бабочки — насекомые». Содержание у них разное, а форма одна и та же: «Все Sесть Р»; она включает S(субъект), т. е. понятие о предмете суждения, Р (предикат), т. е. понятие о признаке предмета, связку («есть»), кванторное слово («все»). Иногда связка может отсутствовать или заменяться тире. Два следующих условных суждения имеют одну и ту же форму: 1) «Если железо нагреть, то оно расширяется»; 2) «Если учащийся изучает логику, то он повышает четкость своего мышления». Форма этих суждений такая: «Если Sесть Р, то Sесть P1». Логические законы Соблюдение законов логики — необходимое условие достижения истины в процессе рассуждения. Основными формальнологическими законами обычно считаются: 1) закон тождества; 2) закон непротиворечия; 3) закон исключенного третьего; 4) закон достаточного основания. Они будут подробно излагаться в отдельной главе. Эти законы (принципы) выражают определенность, непротиворечивость, доказательность мышления. Логические принципы действуют независимо от воли людей, не созданы по их воле и желанию. Они являются отражением связей и отношений вещей материального мира. Общечеловеческий характер принципов формальной логики состоит в том, что во все исторические эпохи люди всех классов, всех наций мыслят по одним и тем же логическим принципам. Кроме формальнологических принципов правильное мышление подчиняется основным законам материалистической диалектики: закону единства и борьбы противоположностей, закону взаимного перехода количественных и качественных изменений, закону отрицания отрицания. Истинность мысли и формальная правильность рассуждений Понятие истинности или ложности относится лишь к конкретному содержанию того или иного суждения. Если в суждении верно отражено то, что имеет место в действительности, то оно истинно, в противном случае оно ложно. Например, суждение «Все волки — хищные животные» истинно, а суждение «Все грибы — ядовиты» ложно. Понятие формальной правильности рассуждения относится лишь к логическим действиям и операциям мышления. Ф. Энгельс писал: «Если наши предпосылки верны и если мы правильно применяем к ним законы мышления, то результат должен соответствовать действительности...»4 Если в числе посылок умозаключения встречается ложная посылка, то при соблюдении правил логики мы в заключении можем получить и истину, и ложь. Чтоб это показать, возьмем такое умозаключение: Все металлы — твердые тела. Ртуть не является твердым телом. Ртуть не является металлом. В этом умозаключении заключение получилось ложным именно потому, что в качестве первой посылки взято ложное суждение. Чтобы заключение было истинным, обе посылки должны быть истинными суждениями (имеется в виду, что правила логики соблюдены). При несоблюдении правил логики (если посылки при этом истинны) мы также можем получить как истинное, так и ложное заключение. Например: Все тигры — полосатые. Это животное — полосатое. Это животное — тигр. Во втором умозаключении обе посылки — истинные суждения, но полученное заключение может быть как ложным, так и истинным потому, что было нарушено одно из правил умозаключения. Итак, с точки зрения содержания мышление может давать истинное или ложное отражение мира, а со стороны формы оно может быть логически правильным или неправильным. Истинность есть соответствие мысли действительности, а правильность мышления — соблюдение законов и правил логики. Нельзя отождествлять (смешивать) следующие понятия: «истинность» («истина») и «правильность», а также понятия «ложность» («ложь») и «неправильность». Материалистическая диалектика — глубокое и всестороннее учение о развитии. Законы и категории материалистической диалектики рассматриваются как отражение всеобщих связей объективного мира и как ступени развития его познания. Современная логика — это интенсивно развивающаяся наука, которая включает в себя логику формальную и логику диалектическую. На их базе формируется логика научного познания, использующая методы обеих наук для анализа научного знания. Как уже отмечалось, формальная логика — наука о законах и формах правильного мышления. Формальная логика в определенном смысле подобна грамматике. К. Д. Ушинский считал логику грамматикой мышления. Подобно грамматике, придающей языку стройный и четко осмысленный характер, логика обеспечивает доказательность и стройность мышления. Основные этапы развития формальной логики Формальная логика в своем развитии прошла два основных этапа. Основанием деления на эти этапы служит различие применяемых в логике средств и методов исследования. Начало первого этапа связано с работами древнегреческого философа и ученого Аристотеля (384—322 гг. до н. э.), в которых впервые дано систематическое изложение логики. Логику Аристотеля и всю доматематическую логику обычно называют «традиционной» формальной логикой. Традиционная формальная логика включала и включает такие разделы, как понятие, суждение, умозаключение (в том числе и индуктивное), законы логики, доказательство и опровержение, гипотеза. Аристотель видел в логике орудие (или метод) исследования. Основным содержанием аристотелевой логики является теория дедукции. В логике Аристотеля содержатся элементы математической (символической) логики, у него имеются «начатки исчисления высказываний»6. Второй этап — это появление математической (или символической) логики. Немецкий философ Г. В. Лейбниц (1646—1716) по праву считается основоположником математической (символической) логики. Начиная с Лейбница в логике используется в качестве метода исследования метод формализации, который традиционной логикой относился только к методам математического исследования, а Лейбниц показал, что он имеет общенаучный характер. Лейбниц пытался построить универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычисления. В XIX в. математическая логика получила интенсивное развитие в работах Д. Буля, Э. Шредера, П. С. Порецкого, Г. Фреге и других логиков. Математическая (или символическая) логика изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода. При этом в математической логике для выявления структуры вывода строятся различные логические исчисления, прежде всего исчисление высказываний и исчисление предикатов в их различных модификациях. Можно сказать, что математическая логика разрабатывает применение математических методов к анализу форм и законов доказательного рассуждения. Другим основанием деления логики служит различие применяемых в ней принципов, на которых базируются исследования. В результате такого деления имеем классическую логику и неклассические логики. В. С. Меськов выделяет такие основополагающие принципы классической логики: «1) область исследования составляют обыденные рассуждения, рассуждения в классических науках; 2) допущение о разрешимости любой проблемы; 3) отвлечение от содержания высказываний и от связей по смыслу между ними; 4) абстракция двузначности высказываний»7. Теоретическое ипрактическое значение логики Можно логично рассуждать, правильно строить свои умозаключения, опровергать доводы противника и не зная правил логики, подобно тому как нередко люди выражают свои мысли на языке, не зная его грамматики. Знание логики повышает культуру мышления, способствует четкости, последовательности и доказательности рассуждения, усиливает эффективность и убедительность речи. Особенно важно знание основ логики в процессе овладения новыми знаниями, в обучении, в ходе подготовки к занятию, при написании сочинения, выступления, доклада; знание логики помогает заметить логические ошибки в устной речи и в письменных произведениях других людей, найти более короткие и правильные пути опровержения этих ошибок, не допускать их самому. В настоящее время особое значение приобретает задача рационального построения процесса обучения в различных учебных заведениях. Экстенсивные методы, предполагающие расширение объема вновь усваиваемой информации, уступают место интенсивным, предполагающим рациональный отбор из всего потока новой информации важнейших, определяющих компонентов. Необходимым условием внедрения новых методов обучения является развитие логической культуры педагогов и учащихся — овладение методологией и методикой научного познания, усвоение рациональных методов и приемов доказательного рассуждения, формирование творческого мышления. Логическая культура — это не врожденное качество. Для ее развития необходимо, прежде всего, ознакомление учителей и студентов педагогических вузов и училищ с основами логической науки, которая в течение двухтысячелетнего развития накопила теоретически обоснованные и оправдавшие себя методы и приемы рационального рассуждения и аргументации. Учителя, знающие основы логики, смогут передать эти знания, умения и навыки правильного, т. е. логического, мышления своим ученикам. Логика способствует становлению самосознания, интеллектуальному развитию личности, помогает формированию у нее научного мировоззрения. Успешное решение сложных задач обучения и воспитания молодежи в решающей степени зависит от учителя, от его интеллектуального уровня, профессионального мастерства, эрудиции и культуры. Профессия учителя требует постоянного творчества, неустанной работы мысли и совершенствования ее культуры, без чего не возможен учительский авторитет среди учащихся. Для улучшения подготовки учительских кадров рекомендуется расширить преподавание логики, изучение которой поможет поднять интеллектуальную культуру будущих учителей. В повседневной жизни, в науке, в обучении каждому ежедневно приходится из одних истинных суждений выводить другие, опровергать ложные суждения или неправильно построенные доказательства. Сознательное следование законам логики дисциплинирует мышление, делает его более аргументированным, эффективным и продуктивным, помогает избежать ошибок, что особенно важно как для учителей, так и для других людей, а для отдельных видов деятельности, например судей, архиважно. Касаясь последнего, Агата Кристи в романе «Десять негритят» пишет: «Купить остров, думал судья, окружить себя атмосферой таинственности вполне в характере Констанции Калмингтон. И судья кивнул головой: он был доволен собой — его логика, как всегда, безупречна...» О значении логики для следователя Уотсон, друг Шерлока Холмса, говорит следующее: «Л не знал большего наслаждения, как следовать за Холмсом во время его профессиональных занятий и любоваться его стремительной мыслью. Порою казалось, что он решает предлагаемые ему загадки не разумом, а каким-то вдохновенным чутьем, но на самом деле все его выводы были основаны на точной и строгой логике» (А. Конан Дойл). § 3. ЛОГИКА И ЯЗЫК Предметом изучения логики являются формы и законы правильного мышления. Мышление есть функция человеческого мозга. Труд способствовал выделению человека из среды животных, явился фундаментом в возникновении у людей сознания (в том числе мышления) и языка. Мышление неразрывно связано с языком. Язык, по выражению К. Маркса, есть непосредственная действительность мысли. В ходе коллективной трудовой деятельности у людей возникла потребность в общении и передаче своих мыслей друг другу, без чего была невозможна сама организация коллективных трудовых процессов. Функции естественного языка многочисленны и многогранны. Язык — средство повседневного общения людей, средство общения в научной и практической деятельности. Язык позволяет передавать и получать накопленные знания, практические умения и жизненный опыт от одного поколения к другому, осуществлять процесс обучения и воспитания подрастающего поколения. Языку свойственны и такие функции: хранить информацию, быть средством выражения эмоций, быть средством познания. Язык является знаковой информационной системой, продуктом духовной деятельности человека. Накопленная информация передается с помощью знаков (слов) языка. Речь может быть устной или письменной, звуковой или незвуковой (как, например, у глухонемых), речью внешней (для других) или внутренней, речью, выраженной с помощью естественного или искусственного языка. С помощью научного языка, в основе которого лежит естественный язык, сформулированы положения философии, истории, географии, археологии, геологии, медицины (использующей наряду с «живыми» национальными языками и ныне «мертвый» латинский язык) и многих других наук. Язык — это не только средство общения, но и важнейшая составная часть культуры всякого народа. На базе естественных языков возникли искусственные языки науки. К ним принадлежат языки математики, символической логики, химии, физики, а также алгоритмические языки программирования для ЭВМ, которые получили широкое применение в современных вычислительных машинах и системах. Языками программирования называются знаковые системы, применяемые для описания процессов решения задач на ЭВМ. В настоящее время усиливается тенденция разработки принципов «общения» человека с ЭВМ на естественном языке, чтобы можно было пользоваться компьютерами без посредников—программистов. Знак — это материальный предмет (явление, событие), выступающий в качестве представителя некоторого другого предмета, свойства или отношения и используемый для приобретения, хранения, переработки и передачи сообщений (информации, знаний). Знаки подразделяются на языковые и неязыковые. К неязыковым знакам относятся знаки-копии (например, фотографии, отпечатки пальцев, репродукции и др.), знаки-признаки, или знаки-показатели (например, дым — признак огня, повышенная температура тела — признак болезни), знаки-сигналы (например, звонок — знак начала или окончания занятия), знаки-символы (например, дорожные знаки) и другие виды знаков. Существует особая наука — семиотика, которая является общей теорией знаков. Разновидностями знаков являются языковые знаки. Одна из важнейших функции языковых знаков состоит в обозначении ими предметов. Для обозначения предметов служат имена. Имя — это слово или словосочетание, обозначающее какой-либо определенный предмет. (Слова «обозначение», «именование», «название» рассматриваются как синонимы.) Предмет здесь понимается в весьма широком смысле: это вещи, свойства, отношения, процессы, явления и т. п. как природы, так и общественной жизни, психической деятельности людей, продуктов их воображения и результатов абстрактного мышления. Итак, имя всегда есть имя некоторого предмета. Хотя предметы изменчивы, текучи, в них сохраняется качественная определенность, которую и обозначает имя данного предмета. Имена делятся на: 1) простые («книга», «снегирь», «опера») и сложные, или описательные («самый большой водопад в Канаде и США», «планета Солнечной системы»). В простом имени нет частей, имеющих самостоятельный смысл, в сложном они имеются; 2) собственные, т. е. имена отдельных людей, предметов, событий («П. И. Чайковский», «Обь»), и общие (названия класса однородных предметов), например «дом», «действующий вулкан». Каждое имя имеет значение и смысл. Значением имени является обозначаемый им предмет8. Смысл (или концепт) имени — это способ, каким имя обозначает предмет, т. е. информация о предмете, которая содержится в имени. Поясним это на примерах. Один и тот же предмет может иметь множество разных имен (синонимов). Так, например, знаковые выражения «4», «2+2», «9—5» являются именами одного и того же предмета: числа 4. Разные выражения, обозначающие один и тот же предмет, имеют одно и то же значение, но разный смысл (т. е. смысл выражений «4», «2+2» и «9 — 5» различен). Приведем другие примеры, разъясняющие, что такое значение и смысл имени. Такие знаковые выражения, как «великий русский поэт Александр Сергеевич Пушкин (1799—1837)», «автор романа в стихах «Евгений Онегин», «автор стихотворения, обращенного к Анне Петровне Керн, «Я помню чудное мгновенье», «поэт, смертельно раненный на дуэли с Ж. Дантесом», «автор исторической работы «История Пугачева» (1834)», имеют одно и то же значение (они обозначают поэта А. С. Пушкина), но различный смысл. Такие языковые выражения, как «самое глубокое озеро мира», «пресноводное озеро в Восточной Сибири на высоте около 455 метров», «озеро, имеющее свыше 300 притоков и единственный исток — реку Ангару», «озеро, глубина которого 1620 метров», имеют одно и то же значение (озеро Байкал), но различный смысл, поскольку эти языковые выражения представляют озеро Байкал с помощью различных его свойств, т. е. дают различную информацию о Байкале. Соотношение трех понятий: «имя», «значение», «смысл» — схематически можно изобразить таким образом (рис. 1). 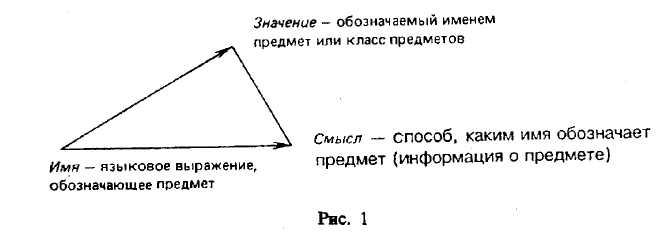 Эта схема пригодна, если имя является не только собственным, т. е. приложимым к одному предмету (число 4, А. С. Пушкин, Байкал), но и общим (например, «человек», «озеро»). Тогда вместо единичного предмета значением имени будет класс однородных предметов (например, класс озер или класс собак и т. д.) и схема останется в силе при данном уточнении, при этом вместо смысла будет содержание понятия. В логике различают выражения, которые являются именными функциями, и выражения, являющиеся пропозициональными функциями. Примерами первых являются «х2+1», «отец у», «разность чисел zи 5»; примерами вторых являются: «х — поэт», «7+у=10», « х >у—7». Рассмотрим эти два вида функций. Именная функция — это выражение, которое при замене переменных постоянными превращается в обозначение предмета. Возьмем именную функцию «отец у». Подставив вместо у имя «писатель Жюль Верн», получим «отец писателя Жюля Верна» — имя предмета (в данном случае имя человека). Именная функция — это такое выражение, которое не является непосредственно именем ни для какого предмета и нуждается в некотором восполнении для того, чтобы стать именем предмета. Так, выражение х2— 1 не обозначает никакого предмета, но если мы его «восполним», подставив, например, на место х имя числа 3 (обозначающее это число цифру), то получим выражение З2 — 1, которое является уже именем для числа 8, т. е. для некоторого предмета. Аналогично выражение х2 + у2не обозначает никакого предмета, но при подстановке на место х и у каких-нибудь имен чисел, например «4» и «1», превращается в имя числа 17. Такие нуждающиеся в восполнении выражения, как х2— 1, х2 + у2, и называют функциями: первая — от одного, вторая — от двух аргументов. Пропозициональной функцией называется выражение, содержащее переменную и превращающееся в истинное или ложное высказывание при подстановке вместо переменной имени предмета из определенной предметной области. Приведем примеры пропозициональных функций: «z— город»; «х есть космонавт»; «у— четное число»; «х + у = 10»; «х3-1 = 124». Пропозициональные функции делятся на одноместные, содержащие одну переменную, называемые свойствами (например, «х — композитор», «х—7 = 3», «z— гвоздика»), и содержащие две и более переменных, называемые отношениями (например, «х > у»; «х—z=16»; «объем куба х равен объему куба у »). Возьмем в качестве примера пропозициональную функцию «х — нечетное число» и, подставив вместо х число 4, получим высказывание: «4 — нечетное число», которое ложно, а подставив число 5, получим истинное высказывание: «5 — нечетное число». Разъясним это на некоторых конкретных примерах. Необходимо указать, какие из приведенных выражений являются именными функциями и какие пропозициональными; определить их местность, т. е. число входящих в выражение переменных, и получить из них имена или предложения, выражающие суждения (истинные или ложные): а) «разность чисел 100 и х». Это именная одноместная функция; например, 100 — 6 есть имя предмета, имя числа 94; б) «х2+у». Это именная двухместная функция; при подстановке вместо х числа 5 и вместо у числа 7 превращается в имя предмета, имя числа 32; в) «у — известный полководец». Это пропозициональная одноместная функция; при подстановке вместо у имени «Александр Васильевич Суворов, родившийся 24 ноября 1730 г.» получим истинное суждение: «Александр Васильевич Суворов, родившийся 24 ноября 1730 г., — известный полководец», выраженное в форме повествовательного предложения; г) «z является композитором, написавшим оперы х и у». Это пропозициональная трехместная функция; превращается в ложное суждение при подстановке вместо z имени «Бизе», вместо х — «Аида», а вместо у — «Травиата», т. е. суждение «Визе является композитором, написавшим оперы «Аида» и «Травиата», выраженное в форме повествовательного предложения. Понятие пропозициональной функции широко используется в математике. Все уравнения с одним неизвестным, которые школьники решают начиная с первого класса, представляют собой одноместные пропозициональные функции, например х+2=7, 10—х =4. Неравенства, содержащие одну или несколько переменных, также являются пропозициональными функциями. Например, х<7 или х2—у>0. Семантические категории Выражения (слова и словосочетания) естественного языка, имеющие какой-либо самостоятельный смысл, можно разбить на так называемые семантические категории, к которым относятся: 1) предложения: повествовательные, побудительные, вопросительные; 2) выражения, играющие определенную роль в составе предложений: дескриптивные и логические термины9. Суждения выражаются в форме повествовательных предложений (например, «Киев — город», «Корова — млекопитающее»). В этих суждениях субъектами соответственно являются «Киев», «корова», а предикатами — «город», «млекопитающее». К дескриптивным (описательным) терминам относятся: 1. Имена предметов — слова или словосочетания, обозначающие единичные (материальные или идеальные) предметы («Аристотель», «первый космонавт», «7») или классы однородных предметов (например, «пароход», «книга», «стихотворение», «засуха», «гвардейский полк» и др.). В суждении «Енисей — река Сибири» встречаются три имени предмета: «Енисей», «река», «Сибирь». Имя предмета «Енисей» выполняет роль субъекта, а имена «река» и «Сибирь» входят в предикат («река Сибири») как его две составные части. 2 Предикаторы— слова и словосочетания, обозначающие свойства предметов или отношения между предметами (например, «порядочный», «синий», «электропроводный», «есть город», «меньше», «есть число», «есть планета» и др.). Предикаторы бывают одноместные и многоместные. Одноместные предикаторы обозначают свойства (например, «талантливый», «горький», «большой»). Многоместные предикаторы обозначают (выражают) отношения. Двухместными предикаторами являются: «равен», «больше», «мать», «помнит» и др. Например, «Площадь земельного участка А равна площади земельного участка В», «Мария Васильевна — мать Сережи». Пример трехместного предикатора: «между» (например, «Город Москва расположен между городами Санкт-Петербург и Ростов-на-Дону»). 3. Функциональные знаки — выражения, обозначающие предметные функции, операции («ctg α», «+», «V-» и др.). Кроме того, в языке встречаются так называемые логические термины (логические постоянные, или логические константы). В естественном языке имеются слова и словосочетания: «и», «или», «если... то», «эквивалентно», «равносильно», «не», «неверно, что», «всякий» («каждый», «все»), «некоторые», «кроме», «только», «тот... который», «ни... ни», «хотя... но», «если и только 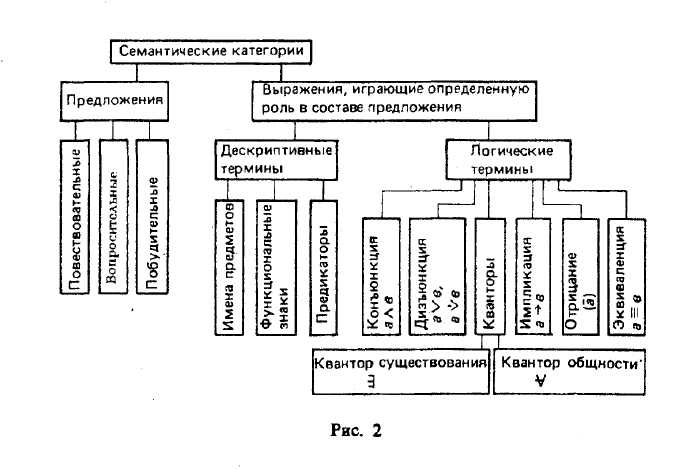 если» и многие другие, выражающие логические константы (постоянные). В символической (или математической) логике в качестве таких констант обычно используются конъюнкция, дизъюнкция, отрицание, импликация, эквиваленция, кванторы общности и существования и некоторые другие. В символической логике логические термины (логические постоянные) выражаются следующим образом: Конъюнкция соответствует союзу «и». Конъюнктивное высказывание обозначается, или, или(например, «Закончились лекции (а), и студенты пошли домой (b)») . Дизъюнкция соответствует союзу «или». Дизъюнктивное суждение обозначается:(нестрогая дизъюнкция) и(строгая дизъюнкция); отличие их в том, что при строгой дизъюнкции сложное суждение истинно только в том случае, когда истинно одно из составляющих суждений, но не оба, а при нестрогой дизъюнкции истинными могут быть одновременно оба суждения. «Он шахматист или футболист» обозначается как«Сейчас Петров находится дома или в институте» обозначается как Импликация соответствует союзу «если... то». Условное суждение обозначается:или(например, «Если будет хорошая погода, то мы пойдем в лес»). Эквиваленция соответствует словам «если и только если», «тогда и только тогда, когда», «эквивалентно». Эквивалентное высказывание обозначается, или, или Отрицание соответствует словам «не», «неверно, что». Отрицание высказывания обозначается(например, «падает снег» (а); «неверно, что падает снег». Квантор общности обозначается и соответствует квантовым словам «все» («всякий», «каждый», «ни один»).•— запись в математической логике (например, в суждении «Все красные мухоморы ядовиты» кванторное слово «все»). Квантор существования обозначается 3 и соответствует словам «некоторые», «существует».—запись в математической логике (например, в суждениях «Некоторые люди имеют высшее образование» или «.Существуют люди, которые имеют высшее образование» кванторные слова выделены курсивом). Выразим в форме схемы разновидности семантических категорий (рис. 2). Примеры 1. Определить дескриптивные и логические термины в суждении: «Все организмы являются одноклеточными или многоклеточными». В этом суждении дескриптивными терминами являются: «организм», «многоклеточный организм», «одноклеточный организм», а логическими терминами: «все», «или». 2. Определить, к каким семантическим категориям относятся следующие выражения: а) листья, упавшие на землю (дескриптивный термин, имя предмета); б) листья упали на землю (суждение, выраженное в форме повествовательного предложения); в) на всякое погруженное в жидкость тело действует выталкивающая сила (суждение, выраженное в форме повествовательного предложения); г) вы пойдете сегодня в библиотеку? (вопросительное предложение, не содержащее суждения); д) брат Ивана (дескриптивный термин, имя предмета). Покажем, каким образом, используя семантические категории, можно выявлять логическую структуру мыслей. Ниже приводятся четыре сложных суждения, структуру которых надо выразить в виде формул, используя введенные логические термины. 1. Если у меня будет свободное время (а) и я сдам экзамены по педагогике (b) и психологии (с), то я поеду отдыхать в Крым (d) или на Кавказ (е). Формула: Здесь буква а обозначает суждение: «У меня будет свободное время»; буква b— суждение: «Я сдам экзамен по педагогике»; буква с — суждение: «Я сдам экзамен по психологии»; буква d— «Я поеду отдыхать в Крым»; буква е — «Я поеду отдыхать на Кавказ». 2. «Если человек с детства и юности своей не давал нервамвластвовать над собой, то они не привыкнут раздражаться и будут ему послушны» (К. Д. Ушинский). Формула: Здесь буква а обозначает суждение: «Человек с детства давал нервам властвовать над собой». А так как у нас имеется отрицание («не давал»), то запишем 3. «И добродетель стать пороком может, когда ее неправильно приложат» (В. Шекспир). Чтобы выявить структуру этого суждения, надо сначала четко выявить основание и следствие, а для этого данное суждение следует привести к четкой логической форме: «Если добродетель неправильно приложат (а), то она может стать пороком (b)». Формула: 4. «Если ребенок вырастил розу для того, чтобы любоваться ее красотой, если единственным вознаграждением за труд стало наслаждение красотой и творение этой красоты для счастья и радости другого человека, — он не способен на зло, подлость, цинизм, бессердечность» (В. А. Сухомлинский). Формула: Задачи к теме «Предмет и значение логики» I. Укажите предметное (денотат) и смысловое (концепт) значения выражений: космонавт, металл, автор комедии в стихах «Горе от ума», орденоносец, писатель, участник Великой Отечественной войны. II. Укажите, какие из приведенных выражений являются именными функциями и какие пропозициональными; определите их местность (одноместная, или двухместная, или трехместная) и получите из них имена или предложения, выражающие высказывания (суждения), — истинные или ложные. 1. Человек х рыжеволос. 2. Разность чисел 15 и z. 3. Сумма х3 +у3. 4. х — современное государство. 5. Ученый у современник ученого z. 6. Натуральное число z больше 100. 7. Река х впадает в море у. 8. х, деленное на 4 без остатка. 9. х2-у2<7. 10. х и у — братья. 11. Город х расположен между городами у и г. 12. Крупные художники х и z, жившие в XVIII в. III. Определите, к каким семантическим категориям относятся следующие выражения: а) собака лает; б) громко лающая собака; в) самая высокая горная вершина мира; г) песня, раздающаяся в ночной тишине; д) песня раздалась в ночной тишине; е) исполнительница народных песен; ж) некоторые фигуры плоские; з) автоматизированная система управления. IV. Придумайте или найдите в литературе 2—3 сложных суждения, содержащих 5—6 простых суждений, и запишите их структуру при помощи символов. V. Выразите в символической форме следующие сложные суждения: 1. Если встать рано на рассвете и пойти в сад или парк, то можно услышать чудесные песни птиц. 2. Если данный четырехугольник — ромб, то диагонали его взаимно перпендикулярны и делят углы пополам. 3. «Видеть несправедливость и молчать — это значит самому участвовать в ней» (Ж.-Ж. Руссо). 4. Если вы любите детей, полны жажды познания, имеете доброе сердце, мечтаете посвятить себя интересному творческому труду, то смело выбирайте профессию учителя. 5. «Если больному после разговора с врачом не становится легче, то это не врач» (В. М. Бехтерев). 6. Добро не умрет, а зло пропадет. 7. Овца руно растит, а скупой деньгу копит — не про себя. 8. Не будет и скуки, как заняты руки. 9. Если Петр проходил мимо работающих, он тотчас же брался помогать: или пройдет ряда два с косой, или навьет воз, или срубит дерево, или порубит дров. 10. «Если верный конь, поранив ногу, Вдруг споткнулся, а потом опять, Не вини коня, вини дорогу, И коня не торопись менять». (Р. Гамзатов). |
