Логика. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики

• Название: Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
• Анкор: Логика.doc
• Дата: 03.05.2018
• Размер: 2.39 Mb.
• Имя файла: Логика.doc
• Тип: Учебник; #18814
• страница: 6 из 25

§ 2. ПРОСТОЕ СУЖДЕНИЕ
Суждения бывают простые и сложные: последние состоят из нескольких простых. Суждение «Некоторые вулканы — действу­ющие» — простое, а суждение «Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка подо льдом блестит» — сложное.
Виды простых суждений

1. Суждения свойства (атрибутивные). В суждениях этого вида утверждается или отрицается принадлежность предмету известных свойств, состояний, видов деятельности. Примеры: «У розы приятный запах», «Певец исполняет арию из оперы «Евгений Онегин», «Всякий терьер — собака», «7 не есть четное чис­ло». Схемы этого вида суждения: Sесть Р или Sне есть Р.

2. Суждения с отношениями. В этих суждениях говорится об отношениях между предметами. Например, «Всякий протон тя­желее электрона», «Эльбрус выше Монблана», «Н. В. Гоголь родился позднее А. С. Грибоедова», «В. Г. Белинский — совре­менник Н. В. Гоголя», «Отцы старше своих детей» и т. д.

Формула, выражающая суждение с двухместным отношени­ем, записывается как аRbили R (а, b), где а и b— имена пред­метов, a R— имя отношения. В суждении с отношением может что-либо утверждаться или отрицаться не о двух, а о трех, четырех или большем числе предметов. Например, «Бологое находится между Санкт-Петербургом и Москвой». Такие сужде­ния выражаются формулой R(a₁ ,а₂ , а₃..., а_n).

3. Суждения существования (экзистенциальные). В них утвер­ждается или отрицается существование предметов (материаль­ных или идеальных) в действительности. Примеры этих сужде­ний: «Существует атомный реактор в Чернобыле», «Не существу­ет беспричинных явлений».
Категорические суждения и их виды (деление do количеству и качеству)

В традиционной логике все три указанных вида представляют простые категорические суждения. По качеству связки («есть» или «не есть») категорические суждения делятся на утвердитель­ные и отрицательные. Суждения «Многие промышленные пред­приятия рентабельны», «Все страусы — птицы» утвердительные. Суждения «Некоторые дома не являются благоустроенными», «Ни один карась не является хищной рыбой» отрицательные. Связка «есть» в утвердительном суждении отражает наличие у предмета (предметов) некоторых свойств. Связка «не есть» отражает то, что предмету (предметам) не присуще некоторое свойство.

Некоторые логики считали, что в отрицательных суждениях нет отражения действительности. На самом деле отсутствие определенных признаков также представляет собой действитель­ный признак, имеющий объективную значимость. В отрицатель­ном истинном суждении наша мысль разъединяет (разделяет) то, что находится разделенным в объективном мире.

В зависимости от того, обо всем классе предметов, о части этого класса или об одном предмете идет речь в субъекте, сужде­ния делятся на общие, частные и единичные. Например, «Все соболя — ценные пушные звери» и «Все здравомыслящие люди хотят долгой, счастливой и полезной жизни» (Поль С. Брэгг) — общие суждения; «Некоторые цветы — розы» — частное; «Везу­вий — действующий вулкан» — единичное.

Структура общего суждения: «Все Sесть (не есть) Р». Единич­ные суждения будут трактоваться как общие, так как их субъек­том является одноэлементный класс.

Среди общих суждений встречаются выделяющие суждения, в состав которых входит кванторное слово «только», — «Только добрый человек может быть врачом» (П. Дюбуа). Примерами выделяющих суждений являются и следующие: «Поль С. Брэгг пил только дистиллированную воду», «Человеческий организм может усваивать только органические вещества», «Смелый чело­век не боится правды. Ее боится только трус» (А. Конан Дойл).

Среди общих суждений имеются исключающие суждения, на­пример: «Все студенты нашей группы, за исключением больных, пришли на семинар». К числу исключающих суждений относятся и те, в которых выражены исключения из правил русского или иных языков, правил логики, математики и других наук.

Частные суждения имеют структуру: «Некоторые Sесть (не есть) Р». Они делятся на неопределенные и определенные. Напри­мер, «Некоторые грибы — съедобны» — неопределенное частное суждение. Мы не установили, обладают ли признаком съедоб­ности все грибы, но не установили и того, что признаком съедоб­ности не обладают некоторые грибы. Если мы установили, что «Только некоторые Sобладают признаком Р», то это будет определенное частное суждение, структура которого: «Только некоторые Sесть (не есть) Р». Примеры: «Только некоторые грибы съедобны»; «Только некоторые остроугольные треуголь­ники являются равносторонними»; «Только некоторые тела легче воды». В определенных частных суждениях часто применяются кванторные слова: большинство, меньшинство, немало, не все, многие, почти все, несколько и др.

Единичные суждения имеют структуру: «Это Sесть (не есть) Р». Примеры единичных суждений: «Эверест — высочайшая вер­шина мира», «Третьяковская галерея в Москве — крупнейший в России музей, где собраны лучшие произведения отечествен­ного искусства».
Объединенная классификация простых категорических суждений по количеству и качеству

В каждом суждении имеется количественная и качественная характеристика. Поэтому в логике применяется объединенная классификация суждений по количеству и качеству, на основе которой выделяются следующие 4 типа суждений.

А — общеутвердительное суждение. Структура его: «Все Sесть Р». Например, «Все люди — позвоночные».

I — частноутвердительное суждение. Структура его: «Некото­рые Sесть Р». Например, «Некоторые элементарные частицы имеют положительный заряд». Условные обозначения для утвер-дительных суждений взяты от слова affirmo — утверждаю (при этом берутся две первые гласные буквы: А — для обозначения общеутвердительного и I — для обозначения частноутвердитель-ного суждения).

Е — общеотрицательное суждение. Его структура: «Ни одно Sне есть Р». Пример: «Ни один дельфин не является рыбой».

О — частноотрицательное суждение. Структура его: «Некото­рые Sне есть Р». Например, «Некоторые люди не являются долгожителями». Условные обозначения для отрицательных суж­дений взяты от слова nego — отрицаю.
Распределенность терминов в категорических суждениях

В суждениях термины Sи Р могут быть либо распределены, либо не распределены. Термин считается распределенным, если его объем полностью включается в объем другого термина или полностью исключается из него. Термин будет нераспределен­ным, если его объем частично включается в объем другого термина или частично исключается из него. Проанализируем четыре вида суждений: А, I, Е, О (мы рассматриваем типичные случаи).

Суждение А общеутвердительное. Его структура: «Все Sесть Р».

Рассмотрим два случая.

1-й случай. В суждении «Все караси — рыбы» субъектом явля­ется понятие «карась», а предикатом — понятие «рыба». Кван­тор общности — «все». Субъект распределен, так как речь идет о всех карасях, т. е. его объем полностью включен в объем предиката. Предикат не распределен, так как в суждении речь идет лишь о той части объема предиката, которая совпадает с объемом субъекта.

Распределенность терминов в суждениях можно иллюстриро­вать с помощью круговых схем Эйлера. На рис. 34 изображено соотношение Sи Р в суждении А. Заштрихованная часть круга на рис. 34—39 характеризует распределенность (или нераспределенность) терминов.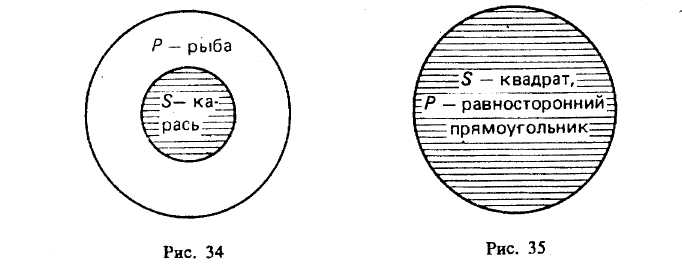



Если объем Р больше (шире) объема S, то Р не распределен.

2-й случай. В суждении «Все квадраты — равносторонние пря­моугольники» термины такие: S— «квадрат», Р — «равносто­ронний прямоугольник», квантор общности — «все». В этом суж­дении Sраспределен и Р распределен, так как их объемы полно­стью совпадают (рис. 35).

Если Sравен по объему Р, то Р распределен. Это бывает в определениях и в выделяющих общих суждениях⁵.

Суждение I частноутвердительное. Его структура: «Некото­рые Sесть Р». Рассмотрим два случая.

1-й случай. В суждении «Некоторые инженеры — филатели­сты» термины такие: S— «инженер», Р — «филателист», кван­тор существования — «некоторые». Соотношение Sи Р изоб­ражено на рис. 36. Субъект не распределен, так как в нем мыслит­ся только часть инженеров, т. е. объем субъекта лишь частично включается в объем предиката. Предикат тоже не распределен, так как он также лишь частично включен в объем субъекта (только некоторые филателисты являются инженерами).

Если понятия S и Р перекрещиваются, то Р не распределен.

2-й случай. В суждении «Некоторые писатели — драматурги» термины такие: S— «писатель», Р — «драматург», квантор су­ществования — «некоторые». Субъект не распределен, так как в нем мыслится только часть писателей, т. е. объем субъекта лишь частично включается в объем предиката. Предикат рас­пределен, так как объем предиката полностью входит в объем субъекта (рис. 37). Таким образом, Р распределен, если объем Р меньше объема S, что бывает в частных выделяющих су­ждениях.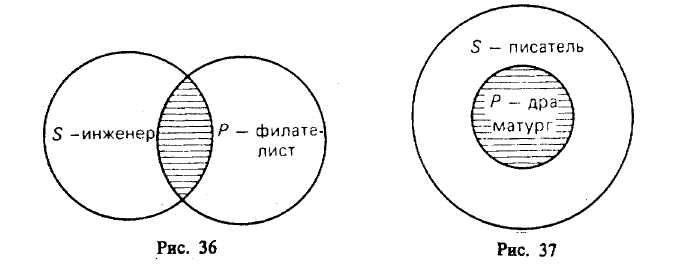



Суждение Е общеотрицательное. Его структура: «Ни одно Sне есть Р ». Например, «Ни один лев не есть травоядное животное». В нем термины такие: S— «лев», Р — «травоядное животное», квантор общности — «ни один». Здесь объем субъек­та полностью исключается из объема предиката, и наоборот. Позтому и S, и Р распределены (рис. 38).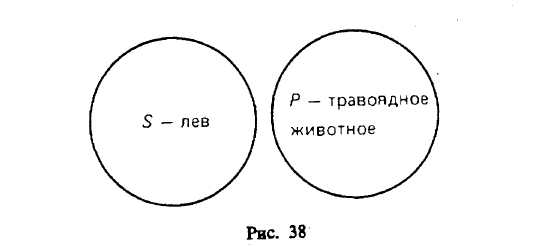



Суждение О частноотрицательное. Его структура: «Некото­рые Sне есть Р». Например, «Некоторые учащиеся не являются спортсменами». В нем такие термины: S— «учащийся», Р — «спортсмен», квантор существования — «некоторые». Субъект не распределен, так как мыслится лишь часть учащихся, а пре­дикат распределен, ибо в нем мыслятся все спортсмены, ни один из которых не включен в ту часть учащихся, которая мыслится в субъекте (рис. 39).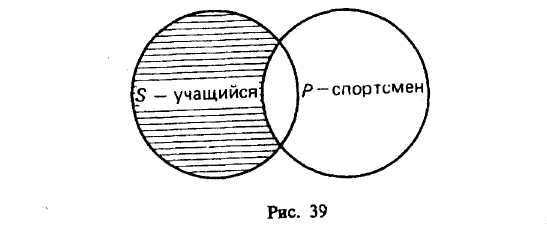



Итак, 5 распределен в общих суждениях и не распределен в частных; Р всегда распределен в отрицательных суждениях, вутвердительных же он распределен тогда, когда по объему

Распределенность терминов в категорических суждениях мож­но выразить в виде следующей схемы (табл. 1), где знаком (+) выражена распределенность термина, а знаком (-) его нераспределенность. В ней же дана объединенная информация о про­стых суждениях.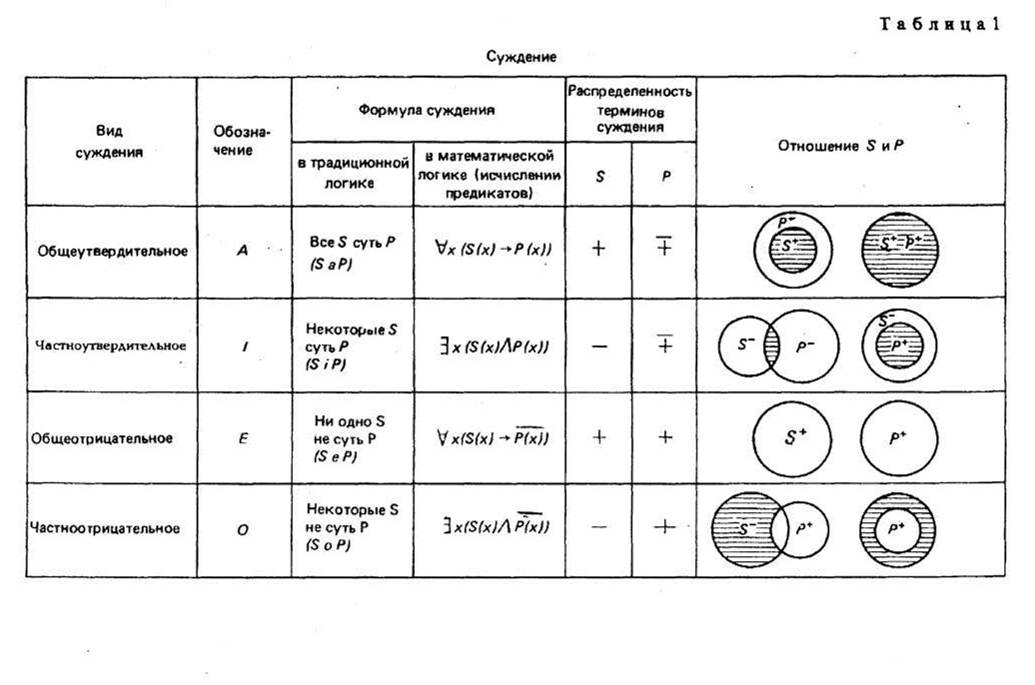


§ 3. СЛОЖНОЕ СУЖДЕНИЕ И ЕГО ВИДЫ
Сложные суждения образуются из простых суждений с помо­щью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания.

Таблицы истинности этих логических связок следующие (табл. 2, 3).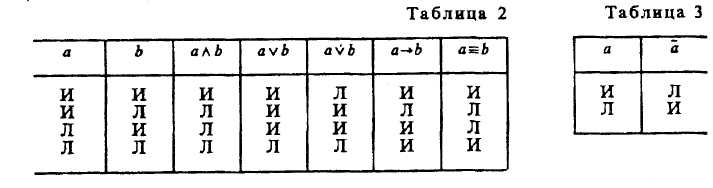



Буквы а, b, с — переменные, обозначающие суждения; буква «И» обозначает истину, а «Л» — ложь.

Таблицу истинности для конъюнкции (а ^ b)можно разъяс­нить на следующем примере. Учителю дали короткую харак­теристику, состоящую из двух простых суждений: «Он является хорошим педагогом (а) и учится заочно (b)». Она будет истинна в том и только в том случае, если суждения а и bоба истинны. Это и отражено в первой строке. Если же а ложно или bложно, либо и а, и bложны, то вся конъюнкция обращается в ложь, т. е. учителю была дана ложная характеристика.

Суждение: «Увеличение рентабельности достигается путем повышения производительности труда (а) или путем снижения себестоимости продукции (b)» — пример нестрогой дизъюнкции. Дизъюнкция называется нестрогой, если ее члены не исключают друг друга. Такое высказывание истинно в том случае, когда истинно хотя бы одно из двух суждений (первые три строки табл. 2), и ложно, когда оба суждения ложны.

Члены строгой дизъюнкцииисключают друг друга. Это можно разъяснить на примере: «Я поеду на юг на поезде (а) или полечу на самолете (b) ». Я не могу одновременно ехать на поезде и лететь на самолете. Строгая дизъюнкция истинна тогда, когда истинно лишь одно из двух простых суждений.

Таблицу для импликацииможно разъяснить на таком примере: «Если через проводник пропустить электрический ток (а), то проводник нагреется (b) »⁶. Импликация истинна всегда, кроме одного случая, когда первое суждение истинно, а второе ложно. Действительно, не может быть, чтобы по проводнику пропустили электрический ток, т. е. чтобы суждение (а) было истинным, а проводник не нагрелся, т. е. суждение (b)было ложным.

Эквиваленция в таблицехарактеризуется так:истинно в тех и только в тех случаях, когда и а, и bлибо оба истинны, либо оба ложны.

Отрицание сужденияхарактеризуется так: если а истинно, то его отрицание ложно, и если а ложно, то а истин­но.

Если в формулу входят три переменные, то таблица истин­ности для этой формулы, включающая все возможные комбина­ции истинности или ложности ее переменных в таблице, будет состоять из 2³ = 8 строк; при четырех переменных в таблице будет 2* = 16 строк; при пяти переменных в таблице имеем 2⁵ = 32 строки; при переменных — 2ⁿ строк (табл. 4, 5).

Алгоритм распределения значений И и Л для перемен­ных (например, для четырех переменных а, b, с, d) таков (табл. 4).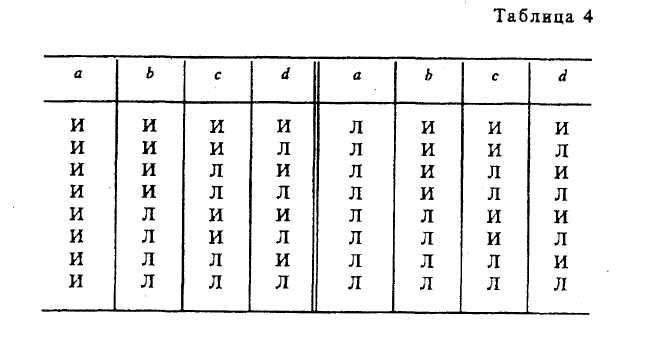



Имеем 2⁴= 16 строк.

В столбце для а сначала пишем 8 раз «И» и 8 раз «Л».

В столбце для bсначала пишем 4 раза «И» и 4 раза «Л», затем повторяем и т. д.

Выполнимая формула та, которая может принимать по край­ней мере одно значение «истина». Тождественно-истинной фор­мулой называется формула, которая при любых комбинациях значений для входящих в нее переменных принимает значение «истина» (иначе она называется законом логики, или тавтологи­ей). Тождественно-ложная формула та, которая соответственно принимает только значение «ложь» (она иначе называется проти­воречием).

Приведем доказательство тождественной истинности фор­мулы: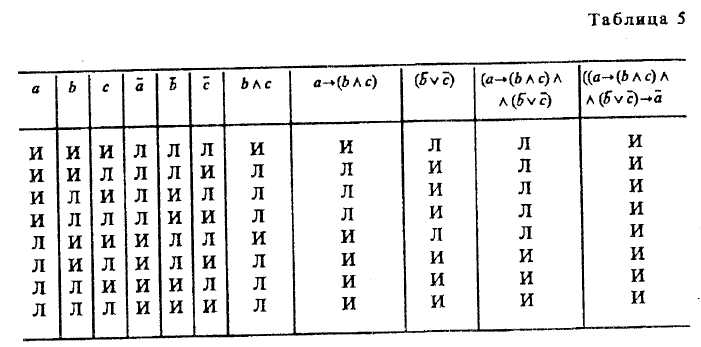


Так как в последней колонке мы имеем только значение «истина», формула является тождественно-истинной, или зако­ном логики (такие выражения называют тавтологиями).

Итак, конъюнкцияистинна тогда, когда оба простых суждения истинны. Строгая дизъюнкцияистинна тогда, когда только одно простое суждение истинно. Нестрогая дизъюнкцияистинна тогда, когда хотя бы одно простое суждение истинно. Импликацияистинна во всех случаях, кроме одного: когда а истинно, a bложно. Эквиваленцияистинна тогда, когда оба суждения истинны или оба ложны. Отрицание (а) истины дает ложь, и наоборот.
Способы отрицания суждений

Два суждения называются отрицающими или противоречащи­ми друг другу, если одно из них истинно, а другое ложно (т. е. они не могут быть одновременно истинными или одновременно ложными) (табл. 6).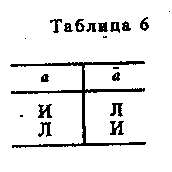



Отрицающими являются следующие пары суждений:

1. А— О. «Все Sесть Р» и «Некоторые Sне есть Р».

2. Е—I. «Ни одно Sне есть Р» и «Некоторые Sесть Р».

3. «Это S есть Р» и «Это Sне есть Р».

Операцию отрицания в виде образования нового суждения из данного следует отличать от отрицания, входящего в состав отрицательных суждений. Существует два вида отрицания: внут­реннее и внешнее. Внутреннее указывает на несоответствие пре­диката субъекту (связка выражена словами: «не есть», «не суть», «не является»). Например, «Некоторые люди не имеют высшего образования». Внешнее отрицание означает отрицание всего суждения. Например, «Не верно, что в Москве протекает река Нева».
Отрицание сложных суждений

Чтобы получить отрицание сложных суждений, имеющих в своем составе лишь операции конъюнкции и дизъюнкции, необ­ходимо поменять знаки операций на противоположные (т. е. конъюнкцию на дизъюнкцию, и наоборот) и над буквами, выра­жающими элементарные суждения, поставить знак отрицания, а если он уже есть, то отбросить его.

Имеем:

1) 2).4)

Эти формулы называются законами ле Моргана. Применив их, получим:

Если в сложном суждении имеется импликация, то ее необ­ходимо заменить на тождественную формулу без импликации (с дизъюнкцией), а именно:; затем по общему методу

найти противоречащее суждение. Например, «Если у меня будет свободное время (а), то я почитаю книгу (b) или посмотрю телевизор (с)». Формула этого сложного суждения: Противоречащее суждение будет:

Оно читается так: «У меня будет свободное время, но я не буду читать книгу и не буду смотреть телевизор».