Логика. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики

• Название: Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
• Анкор: Логика.doc
• Дата: 03.05.2018
• Размер: 2.39 Mb.
• Имя файла: Логика.doc
• Тип: Учебник; #18814
• страница: 3 из 25

Глава II ПОНЯТИЕ

§ 1. ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ

Понятие является одной из форм абстрактного мышления. Конкретные предметы и их свойства отражаются с помощью форм чувственного познания — ощущений, восприятий, предста­влений. Например, в данном апельсине мы ощущаем его свойства — круглый, оранжевый, сладкий, ароматный. Совокупность этих и других свойств дает восприятие (конкретный образ единичного предмета) данного апельсина, при этом мы отража­ем как его существенные свойства, так и несущественные. В понятии же отражаются лишь существенные признаки пред­метов.

Признаки — это то, в чем предметы сходны друг с другом или отличны друг от друга. Свойства и отношения являются призна­ками. Предметы могут быть тождественными по своим свойст­вам (например, сахар и мед сладкие), но могут и отличаться по своим свойствам (мед сладкий, а полынь горькая).

Признаки бывают существенные и несущественные. В понятии отражается совокупность существенных признаков, т. е. таких, каждый из которых, взятый отдельно, необходим, а все вместе взятые достаточны, чтобы с их помощью можно было отличить (выделить) данный предмет от всех остальных и обобщить одно­родные предметы в класс.

Понятие — форма мышления, в которой отражаются сущест­венные признаки одноэлементного класса или класса однородных предметов.

Языковыми формами выражения понятий являются слова или словосочетания (группы слов). Например, «книга», «лес», «гоноч­ная спортивная машина», «спортсмен-перворазрядник». Суще­ствуют слова-омонимы, имеющие различное значение, выража­ющие различные понятия, но одинаково звучащие (например, понятие «мир» как объективная реальность и «мир» как отсутст­вие войны; слово «коса» имеет три различных значения и т. д.). Существуют слова-синонимы, имеющие одинаковое значение, т. е. выражающие одно и то же понятие, но различно звучащие (например, око — глаз, враг — недруг, хворь — болезнь и т. д.).

Основными логическими приемами формирования понятий яв­ляются анализ, синтез, сравнение, абстрагирование, обобщение.

Понятие формируется на основе обобщения существенных признаков (т. е. свойств и отношений), присущих ряду однород­ных предметов.

Для выделения существенных признаков необходимо абст­рагироваться (отвлечься) от несущественных, которых в любом предмете очень много. Этому служит сравнение, сопоставление предметов. Для выделения ряда признаков требуется произвести анализ, т. е. мысленно расчленить целый предмет на его состав­ные части, элементы, стороны, отдельные признаки, а затем осуществить обратную операцию —синтез (мысленное объеди­нение) частей предмета, отдельных признаков, притом признаков существенных, в единое целое.

Мысленному анализу как приему, используемому при образо­вании понятий, часто предшествует анализ практический, т. е. разложение, расчленение предмета на его составные части. Мыс-

ленному синтезу предшествует практический сбор частей пред­мета в единое целое, с учетом правильного взаимного расположе­ния частей при сборке.

Анализ — мысленное расчленение предметов на их составные части, мысленное выделение в них признаков.

Синтез — мысленное соединение в единое целое частей пред­мета или его признаков, полученных в процессе анализа.

Сравнение — мысленное установление сходства или различия предметов по существенным или несущественным признакам.

Абстрагирование — мысленное выделение одних признаков предмета и отвлечение от других. Часто задача состоит в выделе­нии существенных признаков предметов и в отвлечении от несу­щественных, второстепенных.

Обобщение — мысленное объединение отдельных предметов в некотором понятии.

Перечисленные выше логические приемы используются при формировании новых понятий как в научной деятельности, так и при овладении знаниями в процессе обучения.
§ 2. СОДЕРЖАНИЕ И ОБЪЕМ ПОНЯТИЯ
Всякое понятие имеет содержание и объем. Содержанием понятия называется совокупность существенных признаков одно­элементного класса или класса однородных предметов, отражен­ных в этом понятии. Содержанием понятия «ромб» является совокупность двух существенных признаков: «быть параллелог­раммом» и «иметь равные стороны».

Объемом понятия называют класс обобщаемых в нем пред­метов. Объективно, т. е. вне сознания человека, существуют раз­личные предметы, например животные. Под объемом понятия «животное» подразумевается множество всех животных, которые существуют сейчас, существовали ранее и будут существовать в будущем. Класс (или множество) состоит из отдельных объек­тов, которые называются его элементами. В зависимости от их числа множества делятся на конечные и бесконечные. Напри­мер, множество планет Солнечной системы конечно, а множест­во натуральных чисел бесконечно. Множество (класс) А называ­ется подмножеством (подклассом) множества (класса) В, если каждый элемент А является элементом В. Такое отношение между подмножеством А и множеством В называется отноше­нием включения класса А в класс В и записывается так: Это отношение вида и рода (например, класс «ель» входит в класс «дерево»).

Отношение принадлежности элемента а классу А записывает­ся так:(например, а — «Байкал» и А — «озеро»).

Классы А и В являются тождественными (совпадающими), еслии, что записывается как Закон обратного отношения между объемами ж содержаниями понятий

В этом законе речь идет о понятиях, находящихся в родо­видовых отношениях. Объем одного понятия может входить в объем другого понятия и составлять при этом лишь его часть. Например, объем понятия «моторная лодка» целиком входит в объем другого, более широкого по объему понятия «лодка» (составляет часть объема понятия «лодка»). При этом содержание первого понятия оказывается шире, богаче (содержит больше признаков), чем содержание второго. На основе обобщения такого рода примеров можно сформулировать следующий закон: чем шире объем у первого из двух понятий, тем уже его (первого понятия) содержание, и наоборот. Этот закон называется законом обратного отношения между объемами и содержаниями понятий. Он указыва­ет на то, что чем меньше информация о предметах, заключенная в понятии, тем шире класс предметов и неопределеннее его состав (например, «растение»), и наоборот, чем больше информация в понятии (например, «съедобное растение» или «съедобное злако­вое растение»), тем уже и определеннее круг предметов.
§ 3. ВИДЫ ПОНЯТИЙ
Понятия можно классифицировать по объему и по содержа­нию. По объему понятия делятся на единичные, общие и пустые.

Объем единичного понятия составляет одноэлементный класс (например, «великий русский писатель Александр Николаевич Островский»; «столица России» и др.). Объем общего понятия включает число элементов, большее единицы (например, «авто­мобиль», «портфель», «государство» и др.).

Среди общих понятий особо выделяют понятия с объемом, равным универсальному классу, т. е. классу, в который входят все предметы, рассматриваемые в данной области знания или в пре­делах данных рассуждений (эти понятия называют универсаль­ными). Например, натуральные числа — в арифметике; расте­ния — в ботанике; конструктивные объекты — в конструктивной математике и др.

Кроме общих и единичных понятий по объему выделяют понятия пустые (с нулевым объемом), т. е. такие, объем которых представляет пустое множество (например, «вечный двигатель», «баба Яга», «теплород», «человек, проживший 300 лет», «снегу­рочка», «дед Мороз», персонажи сказок, басен и др.).

По содержанию можно выделить следующие четыре пары понятий.
Конкретные и абстрактные понятия

Конкретными называются понятия, в которых отражены од­ноэлементные или многоэлементные классы предметов (как материальные, так и идеальные). К их числу относятся понятия: «дом», «свидетель», «романс», «поэма Владимира Маяковского «Хорошо!», «землетрясение» и др.

Абстрактными называются те понятия, в которых мыслится не целый предмет, а какой-либо из признаков предмета, взятый отдельно от самого предмета (например, «белизна», «несправед­ливость», «честность»). В действительности существуют белые одежды, несправедливые войны, честные люди, но «белизна» и «несправедливость» как отдельные чувственно воспринимае­мые вещи не существуют. Абстрактные понятия, кроме отдель­ных свойств предмета, отражают и отношения между предмета­ми (например, «неравенство», «подобие», «тождество», «сходст­во» и др.).
Относительные и безотносительные понятия

Относительные — такие понятия, в которых мыслятся пред­меты, существование одного из которых предполагает сущест­вование другого («дети» — «родители», «ученик» — «учитель», «начальник» — «подчиненный», «северный полюс магнита» — «южный полюс магнита», «базис» — «надстройка»)¹ .

Безотносительные — такие понятия, в которых мыслятся предметы, существующие самостоятельно, вне зависимости от другого предмета («дом», «человек», «доменная печь», «деревня»).
Положительные и отрицательные понятия

Положительные понятия характеризуют в предмете наличие того или иного качества или отношения. Например, грамотный человек, алчность, отстающий ученик, красивый поступок, эксп­луататор и т. д.²

Если частица «не» или «без» («бес») слилась со словом и слово без них не употребляется (например, «ненастье», «бесчинство», «беспечность», «безупречность», «ненависть», «неряха»), то поня­тия, выраженные такими словами, также называются положи­тельными. В русском языке нет понятий «упречность» или «настье», и частица «не» в приведенных примерах не выполняет функцию отрицания, а поэтому понятия «ненастье», «неряха» и другие являются положительными, так как они характеризуют наличие у предмета определенного качества (может быть, даже и плохого — «неряха», «беспечность»).

Отрицательными называются те понятия, которые означают, что указанное качество отсутствует в предметах (например, «не­грамотный человек», «некрасивый поступок», «ненормальный ре­жим», «бескорыстная помощь»). Эти понятия в языке выражены словом или словосочетанием, содержащим отрицательную ча­стицу «не» или «без» («бес»), присоединенную к соответствующе­му положительному понятию и выполняющую функцию отрицания. Положительное (А) и отрицательное (не-А) являются проти­воречащими понятиями.
Собирательные и несобирательные понятия

Собирательными называются понятия, в которых группа од­нородных предметов мыслится как единое целое (например, «полк», «стадо», «стая», «созвездие»). Проверяем так. Например, об одном дереве мы не можем сказать, что это лес; один корабль не является флотом. Собирательные понятия бывают общими (например, «роща», «студенческий строительный отряд») и еди­ничными («созвездие Большая Медведица», «Российская государ­ственная библиотека», «экипаж космического корабля, впервые осуществивший совместный полет»).

Содержание несобирательного понятия можно отнести к каж­дому предмету данного класса, мыслимого в понятии («ручка», «река», «игрушка»). При этом будут возникать истинные сужде­ния. Например, о каждом данном растении можно сказать, что оно является растением, и это утверждение является истинным.

В суждениях (высказываниях) общие и единичные понятия могут употребляться как в несобирательном (разделительном), так и в собирательном смысле. В суждении «Студенты этой группы успешно сдали экзамен по педагогике» понятие «студент этой группы» является общим и употребляется в разделительном (несобирательном) смысле, так как утверждение об успешной сдаче экзамена по педагогике относится к каждому студенту этой группы. В суждении «Студенты этой группы провели общее собрание» понятие «студенты этой группы» употреблено в соби­рательном смысле, так как студенты этой группы взяты как единый коллектив и это понятие является единичным, ибо данная совокупность студентов (именно этой группы) одна, другого такого коллектива нет.

В целях пояснения приведем следующие примеры.

Дать логическую характеристику понятиям «коллектив», «не­добросовестность», «стихотворение».

«Коллектив» — общее, конкретное, безотносительное, поло­жительное, собирательное.

«Недобросовестность» — общее, абстрактное, безотноситель­ное, отрицательное, несобирательное.

«Стихотворение» — общее, конкретное, безотносительное, положительное, несобирательное.
§ 4. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, отражающие предметы мира, также находятся в определенных отношениях.

Далекие друг от друга по своему содержанию понятия, не име­ющие общих признаков, называются несравнимыми (например, «безответственность» и «нитка»; «романс» и «кирпич»), оста­льные понятия называются сравнимыми.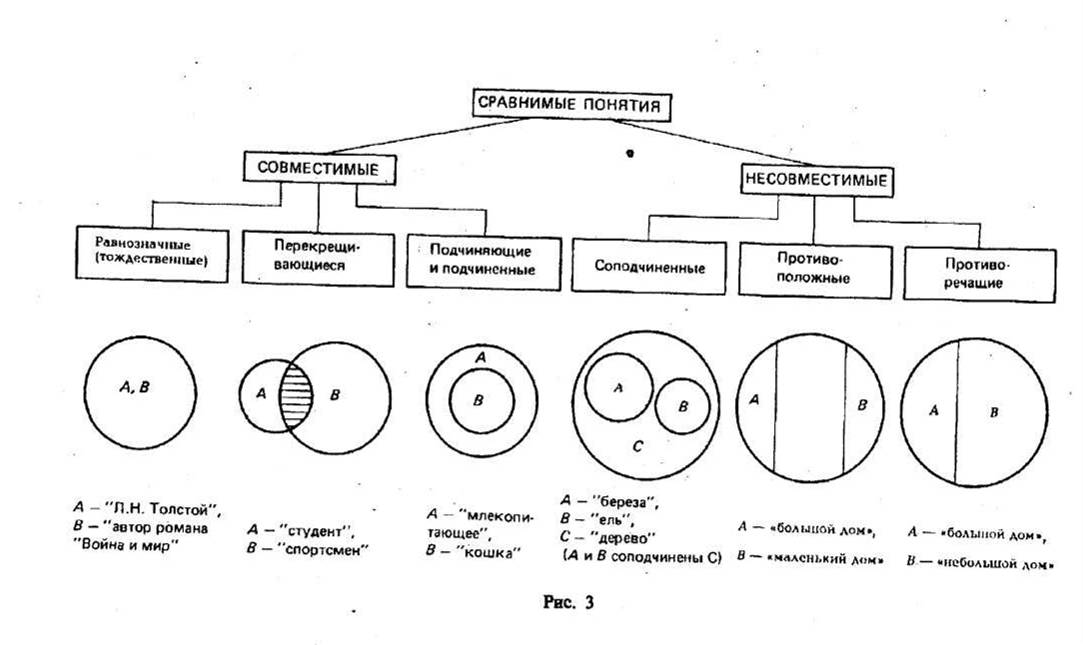


Сравнимые понятия делятся по объему на совместимые (объ­емы этих понятий совпадают полностью или частично) и несов­местимые (объемы которых не совпадают ни в одном элементе).

Типы совместимости: равнозначность (тождество), перекрещивание, подчинение (отношение рода и вида)

Отношения между понятиями изображают с помощью круго­вых схем (кругов Эйлера³), где каждый круг обозначает объем понятия (рис. 3). Если понятие единичное, то оно также изоб­ражается кругом.

Равнозначными (или тождественными) называются понятия, которые различаются по своему содержанию, но объемы кото­рых совпадают, т. е. в них мыслится или одноэлементный класс, или один и тот же класс предметов, состоящий более чем из одного элемента. Примеры равнозначных понятий: 1) «река Вол­га»; «самая длинная река в Европе»; 2) «автор рассказа «Человек в футляре»; «автор комедии «Вишневый сад»; 3) «равносторон­ний прямоугольник»; «квадрат»; «равноугольный ромб». Объемы тождественных понятий изображаются кругами, полностью со­впадающими.

Понятия, объемы которых частично совпадают, т. е. содер­жат общие элементы, находятся в отношении перекрещивания. Примерами их являются следующие пары: «колхозник» и «ор-деноносец»; «школьник» и «филателист»; «спортсмен» и «сту­дент». Они изображаются пересекающимися кругами (см. рис. 3). В заштрихованной части двух кругов мыслятся студенты, явля­ющиеся спортсменами, или (что одно и то же) спортсмены, являющиеся студентами, в левой части круга А мыслятся студен­ты, не являющиеся спортсменами. В правой части круга В мыс­лятся спортсмены, которые не являются студентами.

Отношение подчинения (субординации) характеризуется тем, что объем одного понятия целиком включается (входит) в объем другого понятия, но не исчерпывает его. Это отношение вида и рода; А — подчиняющее понятие («млекопитающее»), В — подчиненное понятие («кошка»).
Типы несовместимости: соподчинение, противоположность, противоречие

Соподчинение (координация) — это отношение между объема­ми двух или нескольких понятий, исключающих друг друга, но принадлежащих некоторому, более общему родовому понятию (например, «ель», «береза», «сосна» принадлежат объему понятия «дерево»). Они изображаются отдельными неперекрещивающимися кругами внутри более обширного круга. Это виды одного я того же рода.

В отношении противоположности (контрарности) находятся объемы таких двух понятий, которые являются видами одного и того же рода, и притом одно из них содержит какие-то призна­ки, а другое эти признаки не только отрицает, но и заменяет их другими, исключающими (т. е. противоположными признака­ми). Слова, выражающие противоположные понятия, являются антонимами. Антонимы широко используются в обучении. При­меры противоположных понятий: «храбрость» — «трусость»; «белая краска» — «черная краска». Объемы последних двух поня­тий разделены объемом некоторого третьего понятия, куда, например, входит «зеленая краска».

В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их ника­кими другими признаками. Если одно понятие обозначить А (на­пример, «высокий дом»), то другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т. е. «невы­сокий дом»). Круг Эйлера, выражающий объем таких понятий, делится на две части (А и не-А) и между ними не существует третьего понятия. Например, бумага может быть либо белой, либо небелой; человек бывает честным или нечестным; живо­тное — млекопитающим или немлекопитающим и т. д. Понятие А является положительным, а понятие не-А — отрицательным.

Понятия А и не-А также являются антонимами.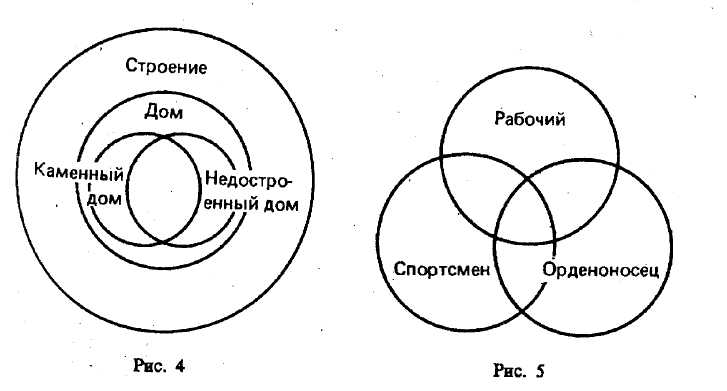



Примеры. Определить отношения между следующими поня­тиями; изобразить эти отношения кругами Эйлера (рис. 4, 5): 1. Дом, недостроенный дом, 2. Спортсмен, рабочий,

каменный дом, строение. орденоносец.
§ 5. ОПРЕДЕЛЕНИЕ ПОНЯТИЙ
Определение (или дефиниция) понятия есть логическая опера­ция, которая раскрывает содержание понятия либо устанавливает значение термина.

С помощью определения понятий мы в явной форме указыва­ем на сущность отражаемых в понятии предметов, раскрываем содержание понятия и тем самым отличаем круг определяемых предметов от других предметов. Так, например, давая определе­ние понятия «трапеция», мы отличаем его от других четыреху­гольников, например от прямоугольника или ромба. «Трапе­ция — четырехугольник, у которого две стороны параллельны, а две другие — не параллельны» (1). Приведем еще несколько определений понятий, взятых из школьных учебников, которые принадлежат к двум различным видам определений. «Вещества, растворы которых проводят электрический ток, называются эле­ктролитами» (2). «Флорой называют видовой состав растений, произрастающих на той или иной территории» (3). «Естествен­ный отбор — процесс выживания наиболее приспособленных особей, который ведет к преимущественному повышению или понижению численности одних особей в популяции по сравнению с другими» (4).

В явном определении понятие, содержание которого надо раскрыть, называется определяемым понятием [definiendum(дефиниендум), сокращенно Dfd], а то понятие, посредством которого оно определяется, называется определяющим понятием [definience(дефиниенс), сокращенно — Dfn].
Реальные и номинальные определения

Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понятие, то определе­ние будет номинальным. Из вышеприведенных определений (1) и (4)—это реальные определения, а (2) и (3) — номинальные

определения.

С помощью номинальных определений вводятся также новые термины, краткие имена взамен более сложных описаний пред­метов. Например, «навыком называют такое действие, в составе которого отдельные операции стали автоматизированными в ре­зультате упражнений».

Путем номинальных определений вводятся и знаки, заменя­ющие термины. Например, «Конъюнкция обозначается знаками ^ или & », «С — скорость света», «Тангенс угла α обозначается как tg α» и т. д.

В номинальном определении часто раскрывается и этимоло­гия того или иного термина. Например, «Термин «философия» происходит от греческих слов «филео» — люблю и «софия» — мудрость, что означает любовь к мудрости (или, как говорили раньше на Руси, любомудрие)».

Для номинальных определений характерно присутствие в их составе слова «называют(ся)». Номинальные определения часто встречаются в учебниках по математике для средней школы. Так, в курсе геометрии встречаются следующие номинальные опреде­ления: «Конус называется круговым, если основание его — круг» или «Круглый конус называют конусом вращения».

Определения делятся на явные и неявные. Явные определе­ния — это такие, в которых даны Dfdи Dfnи между ними устанавливается некоторое отношение равенства, эквивалентно­сти. Самое распространенное явное определение — определение через ближайший род и видовое отличие. В нем устанавливаются существенные признаки определяемого понятия.

Примеры. 1. «Правильный многоугольник — многоуголь­ник, у которого все стороны конгруэнтны и все углы равны».

2. «Барометр — прибор для измерения атмосферного давле­ния».

3. «Гротеск — один из способов сатирического изображения жизни, отличающийся резким преувеличением, сочетанием реаль­ного и фантастического».

Признак, указывающий на тот круг предметов, из числа кото­рых нужно выделить определяемое множество предметов, назы­вается родовым признаком, или родом. В приведенных примерах родовыми являются понятия «многоугольник», «прибор», «спо­соб сатирического изображения жизни».

Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих ро­довому понятию, называются видовым отличием. При определе­нии понятия видовых признаков (отличий) может быть один или несколько.

К явным определениям понятий относятся и генетические определения. Они часто встречаются в школьных учебниках. Гене­тическим называется определение предмета путем указания на способ, которым образуется только данный предмет и никакой другой (это его видовое отличие). Генетическое определение яв­ляется разновидностью определения через род и видовое от­личие.

Приведем примеры генетических определений из области хи­мии. 1. Кислотами называются сложные вещества, образующие­ся из кислотных остатков и атомов водорода, способных заме­щаться атомами металлов или обмениваться на них. 2. Коррозия металлов — это окислительно-восстановительный процесс, обра­зующийся в результате окисления атомов металла и перехода их в ионы.
Использование определений; понятий в процессе обучения

Определение через род и видовое отличие и номинальное определение широко используются в процессе обучения. Приве­дем ряд примеров, взятых из школьных учебников. К определени­ям через ближайший род и видовое отличие можно отнести следу­ющие: «Высшая нервная деятельность — это совокупность мно­жества взаимосвязанных нервных процессов, протекающих в ко­ре головного мозга»; «Наследственностью называют общее свой­ство всех организмов сохранять и передавать признаки строения и функций от предков к потомству». В учебниках по неорганичес­кой химии содержится много номинальных определений понятий, например: «Удержание углем и другими твердыми веществами на своей поверхности частиц газа или растворенного вещества называется адсорбцией». В учебниках физики меньше реальных определений через род и видовое отличие и больше номиналь­ных, например: «Температуру, при которой вещество плавится, называют температурой плавления вещества». В учебнике физики для 7-го класса даны номинальные определения следующим по­нятиям: «теплопередача», «температура отвердевания (или кри­сталлизации)», «удельная теплота плавления», «испарение», «кон­денсация», «температура кипения», «удельная теплота парооб­разования», «сила тока», «электрическая сила» и многим другим. Имеются там и реальные определения. В учебниках географии, наоборот, преимущественное место занимают реальные опреде­ления через род и видовое отличие. Например, «Минерал — при­родное образование (тело), однородное по химическому составу и физическим свойствам». Много определений в учебниках мате­матики, русского языка, истории, литературы и других. Опреде­ление понятий — один из важных и распространенных способов передачи информации в концентрированном виде.

Учитель, овладевая методикой преподавания своего предме­та, должен в первую очередь организовать работу с основными, опорными понятиями и законами, уметь выделить главное в обучении. Повышению теоретического уровня преподавания спо­собствует четкое выделение основных понятий. Надо не только отрабатывать признаки основных и опорных понятий, но и ор­ганично увязывать их содержание с современностью, с практи­кой, в противном случае может возникнуть формализм в знаниях учащихся.

Четкое определение понятия «культура» поможет устранить недостаток в знаниях учащихся, состоящий в том, что они редко относят развитие орудий труда, техники к достижениям культуры, ограничивая свои представления памятниками зодчества, скульптуры, книгопечатания, прикладного искусства, т. е. недо­статочно глубоко изучают достижения материальной культуры. Соответственно двум основным видам производства — мате­риального и духовного — культуру принято делить на матери­альную и духовную, поэтому учителя должны более четко рас­крывать содержание понятии «материальная культура» и «духо­вная культура» и на их базе формировать более общее понятие «культура».

В целом перед учителями стоят такие задачи: добиваться от учащихся глубокого усвоения основных понятий курса, выработ­ки цельной системы раскрытия важнейших понятий школьных предметов, поэтапного расширения их объема и усложнения их структуры. Таков путь усвоения основных, опорных понятий, изучаемых в школьных курсах.
Правила явного определения. Ошибки, возможные в определении

1. Определение должно быть соразмерным, т. е. объем опре­деляющего понятия должен быть равен объему определяемого понятия.Это правило часто нарушается, в результате,

чего возникают логические ошибки в определении. Типы этих логических ошибок:

а) широкое определение, когда Dfd<Dfn. Такая ошибка содер­жится в следующих определениях: «Гравитация — это взаимо­действие двух материальных тел». «Лошадь — млекопитающее и позвоночное животное». (Здесь понятие «лошадь» нельзя от­личить от понятий «корова» или «коза».) Понятие «окружность» неправильно определяется так: «Это фигура, которая описывает­ся движущимся концом отрезка, когда другой его конец закреп­лен, или фигура, которая образована движущимся концом цир­куля». С помощью этого определения нельзя отличить понятие «окружность» от понятия «дуга», так как не указано, что окру­жность — это кривая замкнутая линия;

б) узкое определение, когда Dfd>Dfh. Например, «Совесть — это осознание человеком ответственности перед самим собой за свои действия и поступки» (а перед обществом?). «Производи­тельными силами называются орудия труда, а также и сами люди с их умениями и приемами труда». (В производительные силы входят все средства производства, а не только орудия труда.);

в) определение в одном отношениии широкое, в другом — уз­кое. В этих неправильных определениях Dfd>Dfnи Dfd<Dfn(в разных отношениях). Например, «Бочка — сосуд для хранения жидкостей». С одной стороны, это широкое определение, так как сосудом для хранения жидкостей может быть и чайник, и ведро, и т. д.; с другой стороны, это узкое определение, так как бочка пригодна для хранения и твердых тел, а не только жидкостей. Аналогичная ошибка содержится в определении понятия «учи­тель»: «Учитель — человек, обучающий детей».

2. Определение не должно содержать круга. Круг возникает тогда, когда Dfdопределяется через Dfn, a Dfnбыл определен через Dfd. В определении «Вращение есть движение вокруг своей оси» будет допущен круг, если до этого понятие «ось» было определено через понятие «вращение» («ось — это прямая, вок­руг которой происходит вращение»).

Круг возникает и тогда, когда определяемое понятие харак­теризуется через него же, лишь выраженное иными словами, или когда определяемое понятие включается в определяющее поня­тие в качестве его части. Такие определения носят название тавтологий.

В. И. Ленин, выявив эту логическую ошибку у П. Струве, который дал неверное определение понятия «хозяйство», писал: «Хозяйство определяется через хозяйствование! Масляное мас­ло...»⁵

Тавтологичны такие определения: «Халатность заключается в том, что человек халатно относится к своим обязанностям»; «Количество — это характеристика предмета с его количествен­ной стороны».

Логически некорректным является употребление в мышлении (и в речи) тавтологий, таких, например, как масляное масло, трудоемкий труд, порученное поручение, прогрессирующий про­гресс, ладанная задача, изобрету изобретение, поиграем в игру, памятный сувенир, подытожим итоги и др. Иногда можно встре­тить выражения вида: «Закон есть закон», «Жизнь есть жизнь» и т. д., которые представляют собой прием усиления, а не сообще­ния в предикате какой-то информации о субъекте, так как субъект и предикат тождественны. Такие выражения не претендуют на определение соответствующего понятия: «закон», «жизнь» или др.

3. Определение должно быть четким, ясным. Это правило означает, что смысл и объем понятий, входящих в Dfn, должен быть ясным и определенным. Определения понятий должны быть свободными от двусмысленности; не допускается подмена их - метафорами, сравнениями и т. д.

Не будут определениями следующие суждения: «Архитекту­ра — застывшая музыка», «Лев — царь зверей», «Верблюд — корабль пустыни», «Такт — это разум сердца» (К. Гуцков), «Не­благодарность — род слабости» (И. В. Гёте).
Неявные определения

В отличие от явных определений, имеющих структуру в неявных определениях просто на место Dfnподставляется контекст, или набор аксиом, или описание способа постро­ения определяемого объекта.

Контекстуальное определение позволяет выяснить содержа­ние незнакомого слова, выражающего понятие, через контекст, не прибегая к словарю для перевода, если текст дан на иностран­ном языке, или к толковому словарю, если текст дан на родном языке.

Значения неизвестных в уравнениях даны в неявном виде. Если дано уравнение, первой степени, например 10—y=3, или дано квадратное уравнение, например х² — 7x+12=0, то, решая их и находя значение корней этих уравнений, мы даем явное определение для у (у =7) и для х (x₁ = 4 и х₂ = 3).

Индуктивные определения характеризуются тем, что определя­емый термин используется в выражении понятия, которое ему приписывается в качестве его смысла. Примером индуктивного определения является определение понятия «натуральное число» с использованием самого термина «натуральное число»:

1.1 — натуральное число.

2. Если n— натуральное число, то n +1 — натуральное чи­сло.

3. Никаких натуральных чисел, кроме указанных в пунктах 1 и 2, нет.

С помощью этого индуктивного определения получается на­туральный ряд чисел: 1, 2, 3, 4.....Таков алгоритм построения натуральных чисел.
Определение через аксиомы

В современной математике и в математической логике широ­ко применяется так называемый аксиоматический метод. Приве­дем пример⁶. Пусть дана система каких-то элементов (обознача­емых х, у, z.,.), и между ними установлено отношение, выража­емое термином «предшествует». Не определяя ни самих объек­тов, ни отношения «предшествует», мы высказываем для них следующие утверждения (т. е. следующие две аксиомы):

1. Никакой объект не предшествует сам себе.

2. Если х предшествует у, а у предшествует z, то х предше­ствует z.

Так с помощью двух аксиом определены системы объектов вида « x предшествует у». Например, пусть объектами х, у... являются люди, а отношение между х и у представляет собой «х старше у». Тогда выполняются утверждения 1 и 2. Если объекты х, у, z— действительные числа, а отношение <x предшествует у» представляет собой < x меньше у», то утверждения 1 и 2 также выполняются. Утверждения (т. е. аксиомы) 1 и 2 определяют системы объектов с одним отношением.
Приемы, сходные с определением понятий

Всем понятиям определение дать невозможно (к тому же в этом нет необходимости), поэтому в науке и в процессе обуче­ния используются другие способы введения понятий — приемы, сходные с определением: описание, характеристика, разъяснение посредством примера и др.

Описание состоит в перечислении внешних черт предмета с це­лью нестрогого отличения его от сходных с ним предметов. Описание дает чувственно-наглядный образ предмета, который человек может составить с помощью творческого или воспроиз­водящего представления. Описание включает как существенные, так и несущественные признаки.

Описания широко используются в художественной литературе (например, описание Л. Н. Толстым внешности Анны Карени­ной, описание Н. В. Гоголем внешнего облика Плюшкина, Соба-кевича и других литературных героев, описание Стефаном Цвей­гом облика Оноре Бальзака, облика его отца и других людей, описание пейзажей, деревьев, птиц и т. д.), в исторической лите­ратуре (описание Куликовской битвы, описание обликов военачальников, монархов и других личностей); в специальной технической литературе приводится описание внешнего вида ма­шин, в том числе ЭВМ, описание конструкций различных пред­метов (например, замков, электрохолодильников, электронагре­вательных приборов и др.).

При розыске преступников дается описание их внешности и в первую очередь особых примет, чтобы люди могли их опознать и сообщить об их месте нахождения.

Характеристика дает перечисление лишь некоторых внутрен­них, существенных свойств человека, явления, предмета, а не его внешнего вида, как это делается с помощью описания.

Иногда характеристика дается путем указания одного призна­ка. К. Маркс называл Аристотеля «величайшим мыслителем древности», а Луначарский характеризовал Клима Самгина (из романа М. Горького) как «микроскопическую индивидуальность на больших каблуках самомнения». К. Д. Ушинский писал: «Ле­ность — это отвращение человека от усилий».

В книге рекордов Гиннесса (1988 г.) даны такие характеристи­ки: «Сергей Бубка (СССР). Первый прыгун с шестом, преодоле­вший шестиметровый рубеж»; «Сэр Эдмунд Хиллари (Новая Зеландия). Его выдающееся достижение заключается в том, что он первым покорил Эверест»; «Самая дорогая картина. «Подсол­нухи», одна из серии в 7 картин Винсента ван Гога, была продана на аукционе Кристи 30 марта 1987 г. в Лондоне за 22 500 000 ф. ст.».

Характеристика литературных героев дается путем перечисле­ния их деловых качеств, моральных, общественно-политических взглядов, а также соответствующих действий, черт характера и темперамента, целей, которые они ставят перед собой. Харак­теристика этих персонажей позволяет четко, метко подметить типичные черты того или иного собирательного образа.

Такую, например, характеристику идеального человека дал Аристотель. «Идеальный человек испытывает радость от того, что делает благодеяния другим; но ему стыдно принимать благо­деяние от других. Возвышенные натуры творят добро, низшие натуры принимают его»⁷.

Ж.-Ж. Руссо считал, что можно сделать человека добрее, изменив его потребности. Развивая эту мысль, К. Д. Ушинский дает также характеристики сильного и слабого существа: «Тот, чья сила превосходит его потребности, будь то насекомое, чер­вяк, есть существо сильное; тот же, чьи потребности превосходят силу, будь это слон, лев, будь это победитель, герой, будь это бог, есть существо слабое». И далее: «...чувство доброты появля­ется, когда силы наши превышают требовательность стремле­ний».

Дейл Карнеги дает такую характеристику в сочетании со сравнениями. «Одним из самых трагических свойств человечес­кой натуры, насколько мне известно, является наша склонность откладывать осуществление своих чаяний на будущее. Мы все мечтаем о каком-то волшебном саде, полном роз, который вид­неется где-то за горизонтом, — вместо того, чтобы наслаждаться теми розами, которые растут под нашим окном сегодня. Почему мы такие глупцы — такие ужасающие глупцы? «Как странно мы проводим тот маленький отрезок времени, называемый нашей жизнью, — писал Стивен Ликок. — Ребенок говорит: «Когда я стану юношей». Но что это означает? Юноша говорит: «Когда я стану взрослым». И, наконец, став взрослым, он говорит: «Когда я женюсь». Наконец, он женится, но от этого мало что меняется. Он начинает думать: «Когда я смогу уйти на пенсию». А затем, когда он достигает пенсионного возраста, он оглядывается на пройденный им жизненный путь; как бы холод­ный ветер дует ему в лицо, и перед ним раскрывается жестокая правда о том, как много он упустил в жизни, как все безвозврат­но ушло. Мы слишком поздно понимаем, что смысл жизни заключается в самой жизни, в ритме каждого дня и часа»⁹.

Часто применяется сочетание описания и характеристики. Оно используется при изучении химии, биологии, географии, истории и других наук. Например, «Нефть — маслянистая жидкость, лег­че воды, темного цвета, с резким запахом. Главное свойство нефти — горючесть. При сгорании нефть дает больше теплоты, чем каменный уголь. Нефть залегает глубоко в земле». Этот прием часто используется и в художественной литературе.

Разъяснение посредством примера используется тогда, когда легче привести пример или примеры, иллюстрирующие данное понятие, чем дать его строгое определение через род и видовое отличие.

Объяснение понятия «животный мир пустыни» происходит путем перечисления видов ее обитателей: верблюд, джейран, черепаха, ящерица варан, кулан и др.

Понятие «полезное ископаемое» объясняется перечислением видов (примеров): нефть, каменный уголь, металлы и др. Разъяс­нение посредством примера используется и в средней школе, и в начальной.

Разновидностью этого приема являются остенсивные опреде­ления, к которым часто прибегают при обучении иностранному языку, когда называют и показывают предмет (или картинку с его изображением). Так же иногда поступают при разъяснении непонятных слов родного языка.

Другим приемом, заменяющим определение понятий, являет­ся сравнение. К сравнению прибегают как на уровне научного познания, так и на уровне художественного отображения дейст­вительности. В. А. Сухомлинский использовал сравнение мозга ребенка с цветком розы: «Мы, учителя, имеем дело с самым нежным, самым тонким, самым чутким, что есть в природе, — с мозгом ребенка. Когда думаешь о детском мозге, представляешь нежный цветок розы, на котором дрожит капелька росы. Какая осторожность и нежность нужны для того, чтобы, сорвав цветок, не уронить каплю. Вот такая же осторожность нужна и нам каждую минуту: ведь мы прикасаемся к тончайшему и нежней­шему в природе — к мыслящей материи растущего организ­ма».

В науке сравнение позволяет выяснить сходства и различия сопоставляемых предметов. В учебнике по биологии приводятся такие сравнения: «Тело медузы студенистое, похожее на зонтик»; «Почки — небольшие парные органы, имеющие форму бобов»; «Цветок гороха напоминает сидящего мотылька»; «Завязи пести­ков шиповника скрыты в разросшемся цветоложе, похожем на бокал». Во всех приведенных сравнениях общим признаком (ос­нованием сравнения) является форма.

Сравнение на уровне художественного отображения дейст­вительности позволяет подметить общее, сходное в двух пред­метах, и в яркой форме, образно выразить это сходство. М. Горький использует такое сравнение: «Грубость — такое же уродство, как горб».

Художественные сравнения часто включают в свой состав слова: «как», «как будто», «словно» и др.

Приведем три сравнения людей с животными, которыми пользуется Агата Кристи при характеристике героев в детектив­ном романе «Десять негритят». «Филипп... двигался легко и бес­шумно, как ягуар. И вообще во всем его облике было что-то от ягуара. Красивого хищника — вот кого он напоминал». А вот другое ее сравнение: «Судья... обвел глазами собравшихся и, вытянув шею, как разъяренная черепаха, сказал: — Ядумаю, настало время нам поделиться друг с другом своими сведени­ями». Третий персонаж сравнивается с ящером: «Прикрытые складчатыми, как у ящера, веками глаза остановились на его лице».

В. Набоков в рассказе «Весна в Фиальте» использует такие интересные сравнения: «... елки молча торговали своими голубо­ватыми пирогами»; «... кто-то, спасаясь, падая, хрустя, хохоча с запышкой, влез на сугроб, побежал, охнул сугроб, произвел ампутацию валенка»; «... точно женская любовь была роднико­вой водой, содержащей целебные соли, которой она из своего ковшика охотно поила всякого, только напомни».

Артур Конан Дойл в одном предложении использует сразу три приема, заменяющие определение (приводит описание, хара­ктеристику и ряд сравнений). «Стоит мне и теперь закрыть глаза, Мари встает передо мной: щеки смуглые, как лепестки мускатной розы; взгляд карих глаз нежен и в то же время смел; волосы черные, как смоль, будят волнение в крови и в стихи просятся; а фигурка — точно молодая березка на ветру».

Различение есть прием, позволяющий установить отличие данного предмета от сходных с ним предметов. Например, «Ис­терия — не болезнь, а характер: главная черта этого характера — самовнушаемость» (П. Дюбуа).
Значение определений в науке и в рассуждении

Кроме учета формально-логических требований при опреде­лении понятия надо учитывать и методологические требования к определению. Определение понятия можно сформулировать после всестороннего изучения предмета, и хотя мы никогда не достигнем этого целиком, всесторонность предостережет нас от ошибок и омертвления; необходимо изучение предмета не в ста­тике, а в динамике, в развитии; необходим учет критерия практи­ки и принципа конкретности истины. Исследование есть конкрет­ный анализ конкретной ситуации. Недопустимо смешение поня­тий, использование расплывчатых, неясных формулировок. С учетом методологических требований строится вся научная терминология, и логика должна помочь ученым, представителям частных наук, в систематизации научных терминов.

Методологические требования к определению понятий и формально-логические правила определения, применяемые в единстве с конкретными знаниями, способствуют более чет­кому определению понятий, которыми оперируют в различных науках и в повседневной практике.

Уточнение понятий и терминов, правильное раскрытие их содержания и объема имеют важное значение не только в создании научной терминологии, но и при уточнении смысла слов в обыденных рассуждениях и в составлении различного рода международных договоров. Например, в «Договоре об обычных вооруженных силах в Европе», подписанном на Совещании по безопасности и сотрудничеству в Европе в Париже, в статье II четко определены следующие термины: «группа государств — участников», «район применения», «боевой танк», «боевая бро­нированная машина», «боевая машина с тяжелым вооружением», «артиллерия», «боевой самолет», «обычные вооружения и тех­ника, подпадающие под действие договора» и многие другие.

Без четкого однозначного определения каждого из этих тер­минов просто невозможно было бы обойтись. Приведем пример: «Термин «боевая бронированная машина» означает самоходную машину, обладающую бронезащитой и проходимостью по пере­сеченной местности. Боевые бронированные машины включают бронетранспортеры, боевые машины пехоты и боевые машины с тяжелым вооружением».

Роль определений понятий в науке связана с тем, что опреде­ления, выражая наши знания о предметах мира, являются суще­ственным моментом в познании мира. В каждой науке всем основным понятиям даются определения. В правовых науках точное определение таких понятий, как «взятка», «спекуляция», «необходимая оборона», «преступление», «юридическая ответст­венность», и многих других имеет важное практическое значение.

Относительно роли определения понятия (дефиниции) следует помнить, что от дефиниции понятия нельзя требовать больше того, что она в состоянии дать.