Логика. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики

• Название: Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
• Анкор: Логика.doc
• Дата: 03.05.2018
• Размер: 2.39 Mb.
• Имя файла: Логика.doc
• Тип: Учебник; #18814
• страница: 5 из 25

§ 8. ОПЕРАЦИИ С КЛАССАМИ (ОБЪЕМАМИ ПОНЯТИЙ)
Операции с классами — это такие логические действия, кото­рые приводят нас к образованию нового (в общем случае) класса.

Существуют следующие операции с классами: объединение, пересечение, вычитание, дополнение.
Объединение («сложение») классов

Объединение (или сумма) двух классов — это класс тех элемен­тов, которые принадлежат хотя бы к одному из этих двух клас­сов¹⁷: Объединение обозначается:илиОбъединение класса четных чисел с классом нечетных чисел дает класс целых чисел. Объединив класс поэтов и класс советских поэтов, получим класс поэтов.

При выражении операции объединения классов пользуются обычно союзом «или» в не исключающем смысле. Например, говоря, что некто — член волейбольной или гимнастической сек­ции, мы не исключаем того, что этот человек может быть одно­временно членом обеих секций.

В языке существует и такое употребление союза «или», при котором этот союз понимается в строго разделительном смысле,
например: «Данный глагол первого или второго спряжения». Соответствующая операция над классами называется симмет­рической разностью и в наиболее интересном случае иллюстриру­ется графически так, как это изображено на рис. 8. 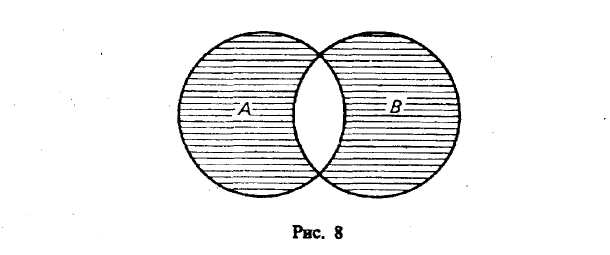Класс, состав­ляющий симметрическую разность классов А и В, на чертеже выделен штриховкой. Симметрическая разность не содержит об­щих членов классов А и В.

При объединении могут встретиться следующие 6 случаев (рис. 9—14).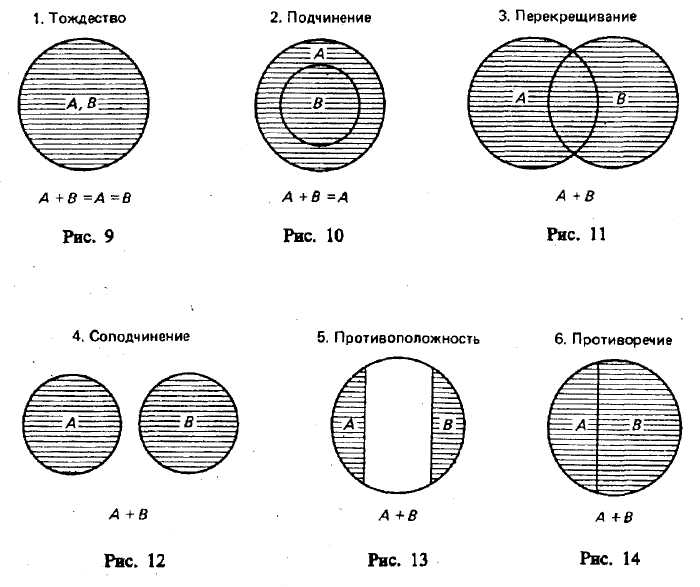


Пересечение («умножение») классов

Общей частью, или пересечением, двух классов называется класс тех элементов, которые содержатся в обоих данных множе­ствах, т. е. это множество (класс) элементов, общих обоим мно­жествам¹⁸. Пересечение обозначаетсяили— пустое множество. При пересечении могут встретиться следующие 6 слу­чаев (рис. 15—20, где результат пересечения заштрихован).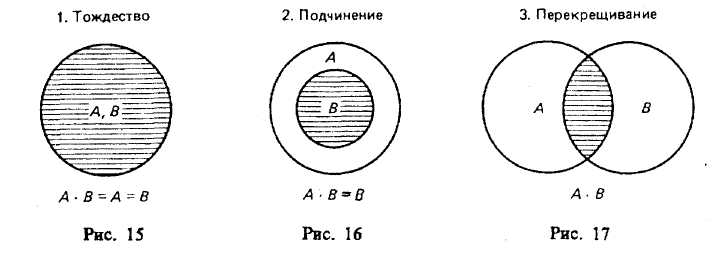



Например, операция пересечения классов «школьник» (А) и «футболист» (В) заключается в нахождении таких людей, кото­рые одновременно являются и школьниками, и футболистами. Это изображено на рис. 17, где общая часть классов А и В за­штрихована.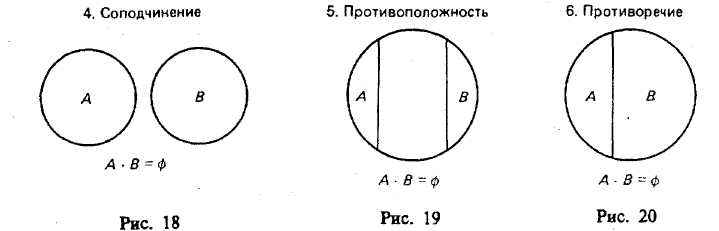



Основные законы логики классов. Законы операций объединения и пересечения

1. Законы идемпотентности.

А + А = А. А х А = А.

В школьном курсе алгебры таких законов нет. В логике первый из этих законов означает следующее. Если мы к классу «дом» прибавим класс «дом», то получим класс «дом», т. е. домов не станет в два раза больше и объем понятия «дом» останется прежним.

2. Законы коммутативности. Эти законы существуют в алгеб­ре, в арифметике, в теории множеств и в логике классов.

А + В = В+А. А В=В А.

Если мы к классу «растение» прибавим класс «животное», то получим класс «организм»; тот же самый класс получим, если мы к классу «животное» прибавим класс «растение».

3. Законы ассоциативности. Они существуют в арифметике, алгебре, теории множеств и в логике классов.

(А+В) + С = А + (В+С). (A х B) х C=A х (B х С).

4. Законы дистрибутивности.

(A+B)C=(A х С)+(B х С). (A х B) + C=(A + С) х (B+С).

5. Законы поглощения. Этих законов нет в арифметике и в школьном курсе алгебры.

А + (А х В)=А. А х (А+В)=А.

Доказательство этих законов осуществляется графическим методом. Два закона поглощения для «сложения» и «умножения» клас­сов иллюстрируются графически на рис. 21 и 22.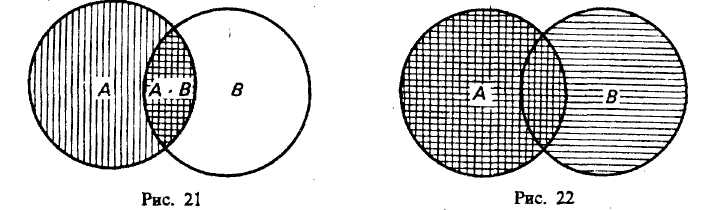



Промежуточный результат изображен горизонтальной штри­ховкой. В первом законе поглощения он равен А В, а во вто­ром — равен А + В. Конечный результат изображен вертикаль­ной штриховкой; он равен классу А.
Вычитание классов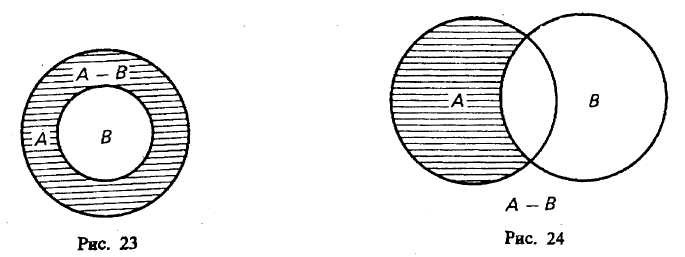



Рассмотрим два множества (класса) А и В, из которых В может и не быть частью А. Разностью множеств (классов) А и В на­зывается множество тех элементов класса А, которые не являют­ся элементами класса В. Разность обозначается А —В.

Могут встретиться следующие пять случаев (если классы А и В не пусты и не универсальны).

1-й случай (рис. 23). Класс А включает в себя класс В. Тогда разностью А — В будет заштрихованная часть А, т. е. множество тех элементов, которые не суть В. Например, если мы из множе­ства звуков русского языка (А) вычтем множество гласных звуков (В), то получим множество согласных звуков, изображенное на чертеже в виде заштрихованного кольца.

2-й случай (рис. 24). Разностью двух перекрещивающихся классов будет заштрихованная часть А. Например, разность мно­жеств «рабочий» (А) и «рационализатор» (В) даст множество рабочих, которые не являются рационализаторами.

3-й случай (рис. 25). Если класс А полностью включен в класс В и класс В полностью включен в класс А, то эти классы (множества) равны (тождественны). Тогда разность А -В даст пустой, или нулевой, класс, т. е. класс, в котором нет ни одного элемента. Например, если мы из класса «сосна» вычтем класс «сосна», то разность А—В будет равна пустому классу.

4-й случай (рис. 26). Класс А и класс В не имеют общих элементов.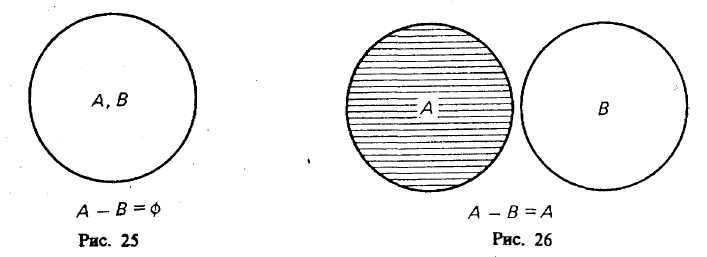


Тогда разность А—В=А, так как всякий элемент класса А не является элементом класса В. Например, разность класса «стол» (А) и класса «стул» (В) равна классу «стол» (А).

В результате «вычитания» классов, соответствующих поняти­ям, находящимся в отношении противоположности [«низкий дом» (А), «высокий дом» (В)] или противоречия [«одушевленный предмет» (А), «неодушевленный предмет» (В)], разность А— В также равна А (рис. 27, 28).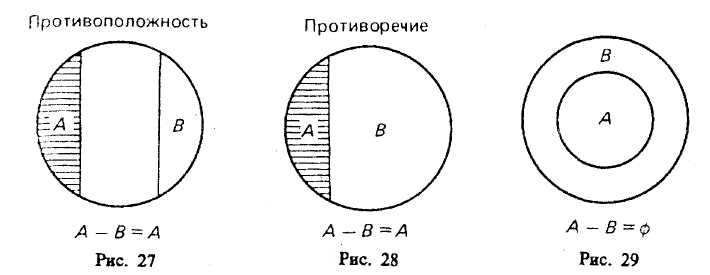



5-й случай (рис. 29). Если объем класса А меньше объема класса В, то в результате вычитания получим пустой класс, так как нет элементов класса А, которые не являлись бы элементами класса В. Например, разность класса «личное местоимение» (А) и «местоимение» (В) дает пустой класс.

Для операции вычитания классов справедливы следующие законы: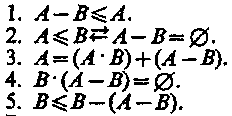


В интерпретации логических алгебр посредством классов за­письобозначает включение класса А в класс В;обозна­чает эквивалентность классов (А тогда и только тогда, когда В ).
Дополнение к классу А

Дополнением к классу А называется класс А" который, будучи сложенным с А, дает рассматриваемую область предметов (эту область обозначим 1), а в пересечении с классом А даетт. е. для которогоОткуда А' = 1- А, поэтому

операцию дополнения к классу А можно рассматривать как частный случай операции «вычитания» (из универсального клас­са). Если от класса целых чисел (1) отнять класс четных чисел (А), то мы получим класс нечетных чисел (т. е. А" поскольку всякое целое число четное или нечетное и нет таких четных чисел, которые были бы нечетными). Графически это можно изобразить так, что заштрихованная часть будет обозначать дополнение к А, т. е. A' (рис. 30).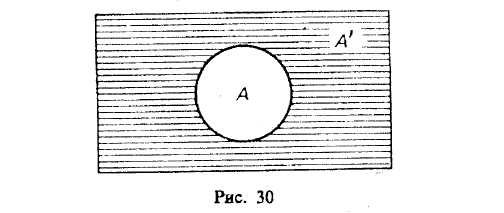



Для операции дополнения кроме указанных выше установ­лены и следующие законы:
Задачи к теме «Понятие»

I. Определить содержание, объем, подклассы объема и элементы объема в следующих понятиях (кавычки опущены): планета Со­лнечной системы; человек, проживший 205 лет; химический эле­мент; вольтметр; факультет педагогического института; закон Ома; материк; русалка; «парад» планет Солнечной системы в 1982 г.

II. Дать логическую характеристику следующим понятиям: мо­лодежный фольклорный ансамбль; Южный полюс; небрежность; газета «Труд»; качество; несовместимость; невежливость; неор­ганическое вещество; отсутствие должной предусмотрительно­сти.

III. Определить отношения между следующими понятиями:

1. Оказание помощи больному, неоказание помощи боль­ному.

2. Каменный дом, трехэтажный дом, одноэтажный дом, недо­строенный дом.

3. Уважение к старшему, неуважение к старшему.

4. Героизм, трусость.

5. Педагогический институт, биологический факультет.

6. Мать, дочь, бабушка, внучка, сестра.

7. Населенный пункт, город, город на Днепре, столица, город Украины.

8. Спутник планеты, естественный спутник, спутник Земли, Юпитер, спутник Юпитера, Луна.

9. Пожар, молния, стихийное бедствие, явление природы.

10. Пожар, причина пожара, взрыв атомной бомбы, поджог.

IV. Дать характеристику (указать вид, состав, правильность) сле­дующих определений:

1. Дентин — особое вещество, покрывающее зубы.

2. Наружное ухо — это ушная раковина.

3. Регенерация — процесс восстановления утраченных или поврежденных частей тела.

4. Жанр — устойчивая форма художественного произведения.

5. Мировоззрение писателя — система его взглядов на окру­жающий мир.

6. Дробь, числитель которой меньше знаменателя, называет­ся правильной.

7. Архаизмы — это слова, вышедшие из употребления вслед­ствие замены их новыми.

8. Рука — орган и продукт труда.

9. Ботаника — наука, изучающая растения.

10. Кость — это орган, обладающий сложным строением.

11. Печень — это крупный орган массой около 1,5 кг.

12. Фразеология — раздел науки о русском языке, изуча­ющий смысловые и структурные особенности фразеологических единиц, их типы и функционирование в речи.

13. Круглый цилиндр можно получить, вращая прямоуголь­ник вокруг одной из его сторон, поэтому круглый цилиндр называется также цилиндром вращения.

14. Окончание—это изменяемая часть слова, с помощью которой образуется определенная грамматическая форма с конкретным грамматическим значением, выражающая грамматичес­кое подчинение данного слова другому слову.

15. Путь крови от левого желудочка через артерии, капил­ляры и вены всех органов тела до правого предсердия называется большим кругом кровообращения.

16. Футуризмом называют одно из декадентских художест­венных течений XX века.

17. Безличными называются предложения, сказуемое кото­рых не допускает при себе подлежащего.

18. Прямой речью называется точно воспроизведенная речь, переданная от лица того, кто ее произнес.

19. Общим делителем нескольких чисел называется число, на которое делится каждое из них.

20. Шар можно получить, вращая полукруг (или круг) вокруг его диаметра.

V. Какие способы введения понятий использованы в приведен­ных ниже примерах (сравнение, различение, описание, характери­стика, разъяснение посредством примера)?

1. «Долг перед отечеством — святыня человека. От нас, от­цов и матерей, от воспитателей, зависит, чтобы каждый наш юный гражданин дорожил этой святыней, как дорожит честный человек своим добрым именем, достоинством своей семьи» (В. А. Сухомлинский).2. Гипофиз расположен в углублении основной кости, похо­жей на турецкое седло.

3. Сердце человека четырехкамерное. В состоянии относи­тельного покоя сердце ритмично сокращается примерно 70—75 раз в минуту. Сокращение обоих предсердий длится около 0,1 секунды. Масса сердца составляет примерно 300 граммов.

4. «Воспитание без дружбы с -ребенком, без духовной об­щности с ним можно сравнить с блужданием в потемках» (В. А. Сухомлинский).

5. Кровяная сыворотка — плазма, в которой уже нет фиб­риногена.

6. Природные компоненты — это горные породы и рельеф их поверхности, вода, воздух, растительность, животный мир и по­чва.

7. «Представьте себе непроходимый экваториальный лес. Ог­ромные деревья стоят, как древние крепости, воздушные мосты из лиан, похожие на толстый кабель, соединяют верхушки дере­вьев на головокружительной высоте. Здесь растут огромные яр­кие грибы, цветы с резким запахом.

Небольшие растения-паразиты ослепительной красоты при­строились на ветвях огромного дерева; постепенно они захваты­вают сетью своих корней весь ствол и медленно душат дерево, пока оно не погибнет» («По материкам и странам». М., 1981).

8. «В 90-летнем возрасте Поль С. Брэгг был силен, подвижен, гибок и вынослив, как юноша. Он ежедневно совершал 3-—5 км пробежки, много плавал, ходил в горы, играл в теннис, танцевал, совершал длительные пешеходные походы, занимался гантелями и гирями, увлекался серфингом — катанием на специальной до­ске в волнах океанского прибоя. Его рабочий день продолжался 12 часов, он не знал болезней и усталости, всегда был полон оптимизма, бодрости и желания помочь людям», — пишет Стив Шенкман¹⁹.

9. «Самый большой чистый самородок. «Приятный незнако­мец», найденный в Мольагуле, Виктория, Австралия, в 1869 г., весил 69,92 кг чистого золота» (Книга рекордов Гиннесса, 1988). VI. Дать характеристику (указать вид, состав, правильность) сле­дующих делений и классификаций. Указать на ошибки, если они имеются.

1. Местоимения по значению делятся на личные, возвратные, притяжательные, указательные, вопросительные, относительные, определительные, отрицательные, неопределенные.

2. Второстепенные члены предложения делятся по своему грамматическому значению на дополнения, определения и обсто­ятельства.

3. Клетки бывают шаровидные, дисковидные, призматичес­кие, кубические, веретенообразные и многогранные.

4. Скелет крыла птицы состоит из одной плечевой кости, двух костей предплечья — локтевой и лучевой — и нескольких костей кисти.

5. Железы делят на железы внешней секреции и железы внут­ренней секреции.

6. Семенные растения делятся на голосемянные и покрытосе­мянные.

7. В эволюции органического мира выделяют два вида от­бора: естественный и искусственный.

8. Щелочи делят на активные и малоактивные.

9. Часы делятся на наручные, настенные, настольные, башен­ные.

10. По назначению транспорт делится так (рис. 31).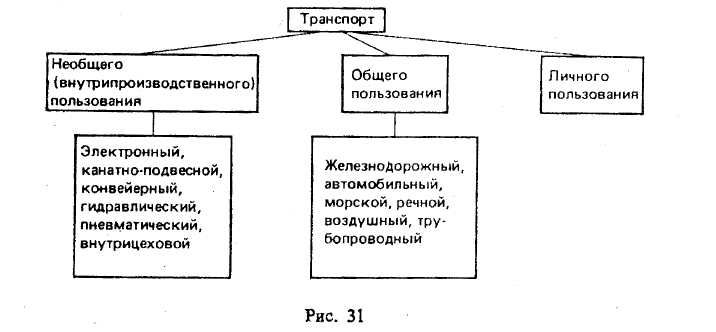



11. Лучи делятся на ультрафиолетовые, видимые и инфра­красные.

12. По механическому составу почвы подразделяются на гли­нистые, суглинистые, супесчаные, песчаные.

13. Основными структурными элементами игры являются: игровой замысел, сюжет игры или ее содержание, игровые дейст­вия, роли, правила.

14. См. рис. 32.

15. Существует несколько видов тепловых двигателей: па­ровая машина, двигатель внутреннего сгорания, паровая тур­бина, газовая турбина, реактивный двигатель.

16. Игрушки делятся на образные, технические, игрушки-за­бавы, маскарадно-елочные, спортивно-моторные, музыкальные я озвученные, театральные, дидактические, строительный мате­риал, игрушки-самоделки.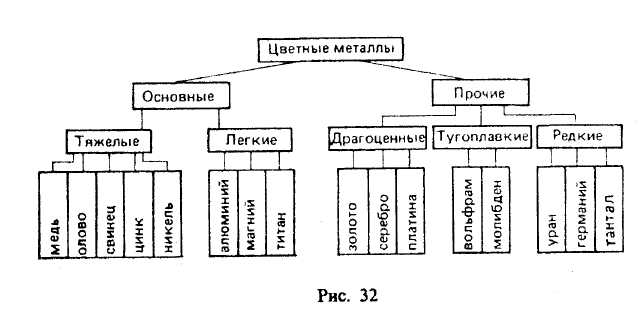



VII. 1. Обобщить и ограничить следующие понятия: река; геоме­трическая фигура; город в Крыму; мораль; студенческий отряд; европеец.

2. Правильно ли проведены ограничения: строение — комна­та; строение — беседка; населенный пункт — столица — центр столицы — центр современной столицы?

VIII 1. Произвести операции над классами А, В, С, изображен­ными на рис. 33 (объединение, пересечение, вычитание).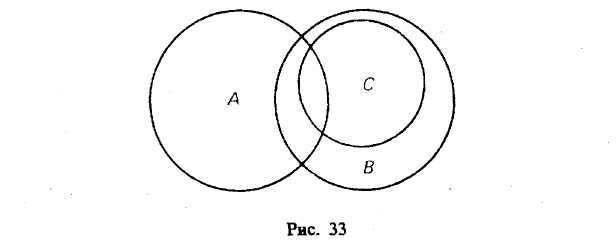



2. Изобразить кругами Эйлера отношение между понятиями: колхозник, хлебороб, орденоносец. Произвести операции над объемами этих понятий (объединение, пересечение, вычитание); найти дополнение к каждому из этих классов и указать его универсум.

Глава III СУЖДЕНИЕ
§ 1. ОБЩАЯ ХАРАКТЕРИСТИКА СУЖДЕНИЯ
Суждение — форма мышления, в которой что-либо утверж­дается или отрицается о существовании предметов, связях между предметом и его свойствами или об отношениях между пред­метами.

Примеры суждений: «Ледоколы существуют», «Советские альпинисты совершили восхождение на Эверест», «Киев больше Тулы», «Все феодалы — эксплуататоры», «Некоторые деревья не являются лиственными». Если в суждении утверждается (или отрицается) наличие у предмета какого-то признака, или кон­статируется существование какого-то предмета, или устанавлива­ется отношение между предметами и это соответствует дейст­вительности, то суждение истинно. Суждения «Все ужи — пре­смыкающиеся», «10 больше 3», «Не существуют русалки», «Неко­торые птицы не являются водоплавающими» являются истин­ными, так как в них адекватно (верно) отражено то, что имеет место в действительности. В противном случае суждение ложно.

Традиционная логика является двузначной, так как в этой логике суждение имеет одно из двух значений истинности: оно либо истинно, либо ложно. В трехзначных логиках суждение имеет одно из трех значений истинности, так как оно может быть либо истинным, либо ложным, либо неопределенным. Например, суждение «На Марсе есть жизнь» в настоящее время не является ни истинным, ни ложным; оно неопределенно. Многие суждения о будущих единичных событиях являются неопределенными. Об этом писал еще Аристотель (IV в. до н. э.), когда приводил пример суждения: «Завтра необходимо будет морское сраже­ние»¹.

В простом атрибутивном суждении имеются субъект, пре­дикат, связка и квантор. В суждениях «Некоторые электростан­ции являются атомными электростанциями» и «Все студенты являются учащимися высшего учебного заведения» субъектами являются соответственно понятия «электростанция» и «студент», предикатами — понятия «атомная электростанция» и «учащийся высшего учебного заведения», кванторами — «некоторые» и «все», связки выражены словом «являются». В суждении «Ледо­колы существуют» субъектом является понятие «ледокол», а предикатом — понятие о существовании предмета, и он выра­жен словами «то, что существует».

Субъект атрибутивного суждения — это понятие о предмете суждения. Предикатом атрибутивного суждения называется по­нятие о признаке предмета, рассматриваемом в суждении. Субъект обозначается буквой S(от лат. subjectum), а предикат — бук­вой Р (от лат. praedicatum). Связка может быть выражена одним словом (есть, суть, является) или группой слов, или тире, или простым согласованием слов («Собака лает», «Идет дождь»). Перед субъектом суждения иногда стоит кванторное слово: «все», или «ни один», или «некоторые» и др. Кванторное слово указыва­ет, относится ли суждение ко всему объему понятия, выражающе­го субъект, или к его части. Простые суждения, о которых шла речь, называются ассерторическими.
Суждение и предложение

Понятия в языке выражаются одним словом или группой слов. Суждения выражаются повествовательными предложени­ями, которые содержат какое-то сообщение, информацию. На­пример, «Буря мглою небо кроет», «Многие лекарственные рас­тения собирают летом», «Ни один дельфин не является рыбой». По цели высказывания предложения делятся на повествователь­ные, побудительные и вопросительные.

Вопросительные предложения не содержат в своем составе суждения, так как в них ничего не утверждается и не отрицается и они не истинны и не ложны. Например, «Как распределяем мы свое свободное время?» или «Когда состоятся соревнования по настольному теннису?». Если в предложении выражен риторичес­кий вопрос, например «Какой русский не любит быстрой езды?» (Н. В. Гоголь), или «Есть ли что-нибудь чудовищнее неблаго­дарного человека?» (В. Шекспир), или «Кто из вас не любит стихов А. С. Пушкина?», или «Кто не хочет счастья?», или «Ка­кой ребенок не хочет материнской ласки?», или «Какой студент не хочет получить стипендию?», в таком предложении содержится суждение, так как налицо утверждение, уверенность, что «Все любят стихи А. С: Пушкина» или «Все хотят счастья» и т. п.²

Побудительные предложения выражают побуждение собесед­ника (читателя и других людей) к совершению действия (пред­ложение может выражать совет, просьбу, обычное побуждение, приказ и т. д,). Некоторые авторы считают, что все побудитель­ные предложения не выражают суждений. По нашему мнению, отдельные побудительные предложения не содержат суждения («Подожди меня!», «Вылей воду!»), хотя в них что-то утверждает­ся («Берегите лес!») или отрицается («Не выливай воду!», «Иди не на каток, а в школу!»). Но предложения, в которых сформулиро­ваны воинские команды, приказы, призывы, или лозунги, или советы, выражают суждения, но не ассерторические, а модаль­ные³. Например: «Ни шагу назад!», «В атаку!», «Мой друг! Отчизне посвятим души прекрасные порывы» (А. С. Пушкин).

Дейл Карнеги в книге «Как перестать беспокоиться и начать жить» дает много интересных советов. Приведем три из них.

«Никогда не пытайтесь свести счеты с вашими врагами, потому что этим вы принесете себе гораздо больше вреда, чем им. Давайте поступать, как генерал Эйзенхауэр: никогда не думайте ни минуты о тех людях, которые вам неприятны». «Если мы хотим обрести счастье, давайте прекратим думать о благодарности или неблаго­дарности, а будем совершать благодеяния ради внутренней радо­сти, которую при этом испытываем». «Помните, что благодар­ность — это такая черта характера, которую надо воспитывать; поэтому, если мы хотим, чтобы наши дети были благодарны, мы должны научить их этому». Эти предложения выражают суждения, но суждения модальные, включающие в себя модальные слова. Выражают суждения и такие побудительные предложения: «Не кури!», «Выполняй взятые на себя обязательства!» и др⁴. «Перед любым приемом пищи ешьте салат из сырых овощей или сырые фрукты», «Не вредите себе перееданием» — эти советы (призывы) знаменитого ученого Поля Брэгга являются суждениями.

Односоставные безличные предложения (например, «Знобит», «Подморозило»), назывные предложения (например, «Утро», «Осень») и некоторые виды повествовательных предложений (на­пример, «Он — отличный вратарь», «Дальний Восток находится от нас далеко») являются суждениями лишь при рассмотрении их в контексте и при уточнении: «Кто — он?», «От кого — от нас?» Если этого уточнения не сделано, то неизвестно, выражает ли данное предложение истину или ложь.

В некоторых случаях не совпадают субъект суждения (5) с грамматическим подлежащим и предикат суждения (Р) с грам­матическим сказуемым. В примере «Студенты — учащиеся» со­впадение полное.

В примере

(здесь прямой линией подчеркнуты подлежащее и сказуемое, а волнистой — логические термины: субъект и предикат); как видим, совпадения нет.

В суждении также нет совпадения.