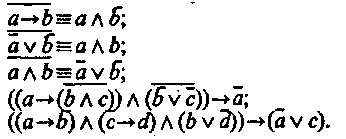§ 4. ВЫРАЖЕНИЕ ЛОГИЧЕСКИХ СВЯЗОК (ЛОГИЧЕСКИХ ПОСТОЯННЫХ) В ЕСТЕСТВЕННОМ ЯЗЫКЕ
В мышлении мы оперируем не только простыми, но и сложными суждениями, образуемыми из простых посредством логических связок (или операций) — конъюнкции, дизъюнкции, импликации, эквиваленции, отрицания, которые также называются логическими константами, или логическими постоянными. Проанализируем, каким образом перечисленные логические связки выражаются в естественном (русском) языке.
Конъюнкция (знак «л») выражается союзами «и», «а», «но», «да», «хотя», «который», «зато», «однако», «не только..., но и» и др. В логике высказываний знак « л » соединяет простые высказывания, образуя из них сложные. В естественном языке союз «и» и другие слова, соответствующие конъюнкции, могут соединять существительные, глаголы, наречия, прилагательные и другие части речи. Например, «В корзине у деда лежали подберезовики и маслята» (ab), «Интересная и красиво оформленная книга лежит на столе». Последнее высказывание нельзя разбить на два простых, соединенных конъюнкцией: «Интересная книга лежит на толе» и «Красиво оформленная книга лежит на столе», — так как создается впечатление, что на столе лежат две книги, а не одна.
В логике высказываний действует закон коммутативности конъюнкции (ab)(ba). В естественном русском языке такого закона нет, так как действует фактор времени. Там, где учитывается последовательность во времени, употребление союза «и» некоммутативно. Поэтому не будут эквивалентными, например, такие два высказывания: 1) «Прицепили паровоз, и поезд тронулся» и 2) «Поезд тронулся, и прицепили паровоз».
В естественном языке конъюнкция может быть выражена не только словами, но и знаками препинания: запятой, точкой с запятой, тире. Например, «Сверкнула молния, загремел гром, пошел дождь».
О выражении конъюнкции средствами естественного языка пишет С. Клини в своей книге «Математическая логика». В разделе «Анализ рассуждений» он приводит (не исчерпывающий) список выражений естественного языка, которые могут быть заменены символами « Л » или «&». Формула А ^ В в естественном языке может выражаться так:
«Не только А, но и В.Как А, так и В.
В, хотя и Л. А вместе с В.
В, несмотря на А. А, в то время как В» 7.
Придумать примеры всех этих структур предоставляем читателю.
В естественном (русском) языке дизъюнкция (обозначенная ab и ab) выражается союзами: «или», «либо», «то ли... то ли» и др. Например, «Вечером я пойду в кино или в библиотеку»; «Это животное принадлежит либо к позвоночным, либо к беспозвоночным»; «Доклад будет то ли по произведениям Л. Н. Толстого, то ли по произведениям Ф. М. Достоевского».
Для обоих видов дизъюнкции действует закон коммутативности: (ab(ba) и (ab)(ba). В естественном языке эта эквивалентность сохраняется. Например, суждение «Я куплю масло или хлеб» эквивалентно суждению «Я куплю хлеб или масло». С. Клини показывает, какими разнообразными способами могут быть выражены в естественном языке импликация (AB) и эквиваленция (AB).
(Буквами А и В обозначены переменные высказывания.)
Приведем логические схемы и соответствующие им примеры, иллюстрирующие разнообразные способы выражения импликации А -> В (где А — антецедент, В — ковсеквент).
1. Если А, то В.
Если поставщики вовремя доставят детали, то завод выполнит свой производственный план.
2. Коль скоро А, то В.
Коль скоро приложенные силы снимаются, то сжатая пружина возвращается к своей первоначальной форме.
3. Когда А, имеет место В.
Когда наступает плохая погода, имеет место повышение числа сердечно-сосудистых заболеваний у людей.
4. Для В достаточно А.
Для того чтобы газы расширились, достаточно их нагреть.
5. Для А необходимо В.
Для сохранения мира на Земле необходимо объединить усилия всех государств в борьбе за мир.
6. А, только если В.
Студенты этого курса не приходили на субботник, только если они были больны.
7. В. если А.
Я разрешу тебе пойти погулять, если ты выполнишь все домашние задания.
Приведем логические схемы и соответствующие им примеры разнообразных способов выражения эквиваленции.
1. А, если и только если В.
Иванов не закончит свои эксперименты к сроку, если и только если ему не помогут сотрудники.
2. Если А, то В, и наоборот.
Если студент сдал все экзамены и практику на «отлично», то он получает диплом с отличием, и наоборот.
3. А, если В, и В, если А.
Многоугольник является вписанным в круг, если его вершины лежат на окружности, и вершины многоугольника лежат на окружности, если этот многоугольник является вписанным в круг.
4. Для А необходимо и достаточно В.
Для того чтобы число без остатка делилось на 3, необходимо и достаточно, чтобы сумма цифр этого числа делилась без остатка на 3.
5. А равносильно В (иногда).
То, что площадь правильного многоугольника равна произведению полупериметра на апофему, равносильно тому, что площадь правильного многоугольника равна произведению периметра на половину апофемы.
6. А тогда и только тогда, когда В.
Фирма будет согласна принять предложение о покупке товара тогда и только тогда, когда будет снижена цена этого товара на 15%.
Из приведенных выше схем и соответствующих им высказываний с конкретным разнообразным содержанием становится ясно, насколько многогранны в естественном языке (в частности, в русском) средства выражения импликации, эквиваленции и других логических связок (логических терминов). Это можно сказать и о других естественных языках9.
Импликация (ab) не совсем соответствует по смыслу союзу «если... то» естественного языка, так как в ней может отсутствовать содержательная связь между суждениями а и b. В логике высказываний законом является формула:(ab)(ab).
Но в естественном языке дело обстоит иначе. Иногда союз «если, то» выражает не импликацию, а конъюнкцию. Например, «Если вчера было пасмурно, то сегодня ярко светит солнце». Это сложное суждение выражается формулой ab. Кроме логических связок для выражения общих и частных суждений в логике используются квантор общности и квантор существования. Запись с квантором общности VP() обычно читается так: «Все х (из некоторой области объектов) обладают свойством Р», а запись с квантором существования ЗхР(х) читается так: «Существуют такие х (в данной области), которые обладают свойством Р». Например, 3x(x>100) читается как «Существуют такие х, которые больше 100», где под х подразумеваются числа. Квантор общности выражается словами: «все», «всякий», «каждый», «ни один» и др. Квантор существования выражается словами: «некоторые», «существуют», «большинство», «меньшинство», «только некоторые», «иногда», «тот, который», «не все», «многие», «немало», «немногие», «много», «почти все» и др.
С. Клини пишет о том, что, переводя выражения обычного языка с помощью табличных пропозициональных связок, мы лишаемся некоторых оттенков смысла, но зато выигрываем в точности10.
В практике математических и иных рассуждений имеются понятия «необходимое условие» и «достаточное условие». Условие называется необходимым, если оно вытекает из заключения (следствия). Условие называется достаточным, если из него вытекает заключение (следствие). В импликации а -> bпеременная а является основанием. Она называется антецедентом. Переменная b— следствием (заключением). Она называется консеквентом.
Учащимся на уроках математики предлагаются задачи типа 1—4, требующие в каждом из следующих предложений вместо многоточия поставить слова: «необходимо» или «достаточно», либо «необходимо и достаточно»:
1. Для того чтобы сумма двух целых чисел была четным числом ... чтобы каждое слагаемое было четным.
2. Для того чтобы число делилось на 15 ... чтобы оно делилось на 5.
3. Для того чтобы произведение (х - 3) (х+2) (х — 5) было равно 0, ... чтобы х = 3.
4. Для того чтобы четырехугольник был прямоугольником ... чтобы все его углы были равны11.
§ 5. ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ ПО ЗНАЧЕНИЯМ ИСТИННОСТИ
Суждения, как и понятия, делятся на сравнимые (имеют общий субъект или предикат) и несравнимые. Сравнимые суждения делятся на совместимые и несовместимые.
В математической логике два высказывания р и qназываются несовместимыми, если из истинности одного из них необходимо следует ложность другого (т. е. pиqникогда не могут оказаться одновременно истинными). «Это понятие легко распространить на любое число высказываний: высказывания р1 , р2 , ..., рn, называются несовместимыми, если не может оказаться, что все они являются одновременно истинными»12.
Совместимые выражают одну и ту же мысль полностью или лишь в некоторой части. Отношения совместимости: эквивалентность, логическое подчинение, частичное совпадение (субконтрарность). Совместимые эквивалентные суждения выражают одну и ту же мысль в различной форме («Юрий Гагарин — первый космонавт» и «Юрий Гагарин первым полетел в космос»). Субъект здесь один и тот же, а предикаты различные по форме, но одинаковые по смыслу. В двух эквивалентных суждениях: «Михаил Шолохов — лауреат Нобелевской премии» и «Автор романа «Тихий Дон» — лауреат Нобелевской премии» — одинаковыми являются предикаты, а различными по форме выражения, но тождественными понятиями — субъекты. Если два высказывания эквивалентны, то невозможно, чтобы одно из них было истинным, а другое ложным.
В сочинении, при заучивании материала, в устном изложении текста, при переводе с одного языка на другой — всюду учащиеся должны уметь кратко и корректно излагать свои мысли. А. П. Чехов дал такое сравнение: «Краткость — сестра таланта».
Совместимые суждения, находящиеся в отношении логического подчинения, имеют общий предикат; понятия, выражающие субъекты двух таких суждений, также находятся в отношении логического подчинения. Отношения между суждениями по истинности принято схематически изображать в виде «Логического квадрата» (рис. 40).

Возьмем суждение «Все учащиеся нашей группы — спортсмены». Это суждение А общеутвердительное (подчиняющее). Суждение I — «Некоторые учащиеся нашей группы — спортсмены» — подчиненное.
Для суждении А иI, а также Е и О, находящихся в отношении логического подчинения, истинность общего суждения определяет истинность частного, подчиненного суждения. Но ложность общего суждения оставляет частное суждение неопределенным. Истинность частного суждения оставляет общее суждение неопределенным (при нарушении этого правила может возникнуть логическая ошибка — «поспешное обобщение»). Ложность частного суждения обусловливает ложность общего суждения. Если истинно суждение «Ни одна трапеция не является сферическим телом», то будет истинным и суждение «Некоторые трапеции не являются сферическими телами». Умозаключение от общего суждения к логически подчиненному ему частному суждению всегда будет давать истинное заключение.
В отношении частичного совпадения (субконтрарности) находятся два таких совместных суждения I и О, которые имеют одинаковые субъекты и одинаковые предикаты, но различаются по качеству. Например, I — «Некоторые свидетели дают истинные показания» и О — «Некоторые свидетели не дают истинных показаний». Оба они одновременно могут быть истинными, но не могут быть одновременно ложными. Если одно из них ложно, то другое обязательно истинно. Но если одно из них истинно, то другое неопределенно (оно может быть либо истинным, либо ложным). Например, если истинно суждение I — «Некоторые книги в этой библиотеке — букинистические», то суждение О — «Некоторые книги в этой библиотеке не являются букинистическими» — будет неопределенным, т. е. оно может быть как истинным, так и ложным.
Отношения несовместимости: противоположность, противоречие. По логическому квадрату в отношении противоположности (контрарности) находятся суждения А и Е. Два суждения: А — «Все люди трудятся добросовестно» и Е — «Ни один человек не трудится добросовестно» — оба ложны. Но А и Е не могут быть оба истинными. Если одно из противоположных суждений истинно, то другое будет ложным.
Итак, из истинности одного из противоположных суждений вытекает ложность другого, но ложность одного из них оставляет другое суждение неопределенным.
В отношении противоречия (контрадикторности) находятся суждения А и О, а также Е и I. Два противоречащих суждения не могут быть одновременно истинными и одновременно ложными. Если в настоящее время истинно суждение I — «Некоторые летчики — космонавты», то ложным будет суждение «Ни один летчик не является космонавтом».
Закономерности, выражающие отношения между суждениями по истинности, имеют большое познавательное значение, так как они помогают избежать ошибок при непосредственных умозаключениях, производимых из одной посылки (одного суждения).
§ 6. ДЕЛЕНИЕ СУЖДЕНИЙ ПО МОДАЛЬНОСТИ
В логике мы до сих пор рассматривали простые суждения, которые называются ассерторическими, а также сложные суждения, составленные из простых. В них утверждается или отрицается наличие определенных связей между предметом и его свойствами или констатируется отношение между двумя или большим числом предметов. Например, «Школьники — учащиеся»; «Объем конуса равен 1/3 площади основания, умноженной на высоту»; «Яблоко сладкое и красное»; «Я эту работу не выполню в срок»; «Если будет плохая погода, то мы не поедем на теплоходе» и др. Общая форма таких простых высказываний (суждений): «5 есть (не есть) Р». Из простых суждений образуются сложные. Например, «Если Sесть (не есть) Р, то S1 есть (не есть) P1».
В этих ассерторических суждениях не установлен характер связи между субъектом и предикатом. Характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном суждении раскрывается в модальном суждении. Из вышеприведенных суждений можно образовать такие, например, модальные суждения: «Несомненно, что все школьники — учащиеся», «Доказано, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы», «Хорошо, что яблоко сладкое и красное», «Возможно, что я эту работу не выполню в срок», «Вероятно, что если будет плохая погода, то мы не поедем на теплоходе». Мы видим, что модальные суждения не просто утверждают или отрицают некоторые связи, а дают оценку этих связей с какой-то точки зрения.
О предмете А можно просто сказать, что он имеет свойство В (это будет ассерторическое суждение). Но можно сверх того уточнить, является ли эта связь А и В необходимой или, наоборот, случайной; хорошо ли, что А есть В или это плохо; доказано, что А есть В или не доказано, а только есть предположение, и т. д. В результате таких уточнений мы получаем модальные суждения различных типов. Приведем другие примеры модальных суждений: «Возможно, на Марсе есть жизнь», «Доказано, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, т. е. а2 + b2=с2»; «При красном свете светофора проезд транспорта запрещен» и др. В модальном суждении к ассерторическому суждению приписывается тот или иной модальный оператор (модальное понятие): возможно, доказано, необходимо, запрещено, обязательно, плохо и др.Структура простых модальных суждений такая: М (Sесть Р) или М (Sне есть Р),
где М обозначает модальный оператор (модальное понятие).
Но как было уже сказано, модальными могут быть и сложные суждения. Если а и b— простые суждения, то из сложных ассерторических суждений: ab, ab, ab, ab, ab — можно получить соответствующие сложные модальные суждения: M (ab); M (ab); M (ab); M (ab); M (ab).


В каждую из групп модальностей входят три основных модальных понятия. Второе из них называется слабой характеристикой, первое и третье — соответственно сильной положительной и сильной отрицательной характеристиками. Иногда в дополнение к трем основным модальным понятиям вводится четвертое, которое может употребляться для обозначения объединения сильного положительного и нейтрального.
Логические и онтологические модальности объединяются вобщий вид — алетические модальности14. Они включают такие модальные операторы или категории модальности: необходимость и случайность, возможность и невозможность. Слова «необходимо», «возможно», «случайно» в обыденном языке употребляются в самых различных смыслах.
Диалектико-материалистическая философия изучает категории «необходимость», «случайность», «возможность» и другие с их содержательной стороны. Формальная логика изучает существующие между ними формальные зависимости. Всеобщность модальных категорий состоит в их приложимости к любой области действительности.
Алетические модальности обозначаются так: « А» — «необходимо А»; « А»— «случайно Л»; « ◊ А» — «возможно А»;x
◊A — «невозможно А»(знак «»обозначает отрицание).
Иногда их обозначают так: «Lp»— «необходимо р», «Мр»— « возможно» .
Алетические модальности (логические и онтологические) часто содержательно истолковывают так: необходимыми считают логические законы, а также законы, выявленные различными науками (естественными, математическими, общественными и техническими), и все следствия из этих законов. Невозможными считают суждения, противоречащие этим законам, отрицания этих законов или их следствий. Случайными считают суждения, не являющиеся законами или их следствиями, но и не противоречащие законам или их следствиям. Возможными считают сложения, не противоречащие законам или их следствиям.Взаимосвязь алетических модальностей
Некоторые алетическне модальности в ряде систем можно определять одну через другую («=» обозначает «равно по определению», «»— конъюнкцию, «» —дизъюнкцию, «» отрицание, «»— эквивалентно, «» — импликацию). Например,
А=
Некоторые важные связи, характеризующие алетические модальности, выражены следующими формулами:
(1) («Earnнеобходимо, что А, то А»);
(2) («Если А, то возможно, что А»);
(3) («Необходимо, что А, тогда и только тогда, когда невозможно, что не-А»);
(4) («Возможно, что А, тогда и только тогда, когда не необходимо, что не-А»).
Задачи к теме «Суждение»
I.Являются ли следующие формулы законами логики:
1) 2) 3) 4) 5)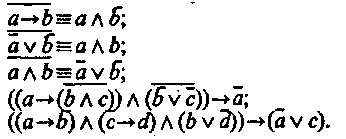
II. Определить вид суждения, его термины и их распределенность в следующих суждениях:
1. Иногда люди опаздывают на работу.
2. Все распространенные предложения имеют второстепенные члены.
3. Некоторые спортсмены не являются мастерами спорта.
4. Вода, нагретая до 80°С, не кипит.
5. Цыплят по осени считают.
6. Общественное бытие определяет общественное сознание.
7. Ни один учитель нашей школы не является отличником народного просвещения.
8. «Некоторые лекарства опаснее самих болезней» (Сенека).
9. «Никакая причина не извиняет невежливость» (Т. Г. Шевченко) .
10. Среда — третий день недели.
11. Некоторые люди не изучают логику.
III. Определить вид и логическую форму следующих сложных высказываний. Записать их структуру в виде формулы:
1. Покрылись зеленью сопки, освобождаются от снега вулканы, в скверы, на улицы Петропавловска-Камчатского в июне высажены деревья, кустарники, готовятся клумбы под цветы.
2. Этот приезд не является ни необходимым, ни желательным.
3. Поиски врага длились уже три часа, но результатов не было, притаившийся враг ничем себя не выдавал.
4. Если эта фигура квадрат, то диагонали в ней равны, взаимно перпендикулярны и в точке пересечения делятся пополам.
5. «Если вы желаете себе несокрушимого памятника, вложите свою душу в хорошую книгу» (Б. Буаст).
IV. Произвести отрицание следующих сложных суждений, предварительно записав в виде формулы их структуру.
1. Если мне дадут отпуск летом, то я поеду отдыхать к морю или по туристической путевке в Карпаты.
2. Неверно, что этот писатель — драматург или поэт.
V. Определить с помощью «логического квадрата» отношения между следующими простыми суждениями:
1. Неверно, что все дети послушны — Некоторые дети являются послушными.
2. Все книги — рукописные — Ни одна книга не является рукописной.
VI. Определить вид модальности в следующих суждениях:
1. С появлением средств генной инженерии можно предвидеть значительные успехи в улучшении качества и состава микробиологической продукции.
2. Вероятно, молоко было одним из первых продуктов сельского хозяйства.
3. Хлебопечение возникло на заре развития человечества, вероятно, в Египте.
4. Необходимо соблюдать правила поведения в общественных местах.
5. Разрешен проезд автомобилей при зеленом свете светофора.
6. Невозможно построить вечный двигатель.
7. «Никогда не беспокой другого тем, что ты можешь сам сделать» (Л. Н. Толстой).
8. «В специально оборудованных вольерах для содержания горилл в зоопарках должны быть деревья, по которым они могли бы лазать, а также солома, ветки или бамбук для сооружения гнезд. Пищу следует давать небольшими порциями на протяжении всего дня, причем в таком виде, чтобы животные имели возможность заниматься ее подготовкой (скажем, обдирать кожицу или расщеплять стебли) или поиском, для чего лучше беспорядочно разбрасывать съедобные растения в вольере. Гориллам нужно обеспечить возможность пребывания на свежем воздухе» (курсив наш. — А. Г.) (Дайан Фосси).
VII. Являются ли суждениями следующие предложения:1. «Что без тебя просторный этот свет? Ты в нем одна. Другого счастья нет». (В. Шекспир).
2. В каком году родился писатель А. Толстой?
3. Принеси мне книгу в среду вечером.
4. Не в свои сани не садись.
5. «Кто не проклинал станционных смотрителей, кто с ними не бранился?» (А. С. Пушкин).
6. «Каких цветов в саду весеннем нет!» (В. Шекспир).
7. «И казалось, что после конца Никогда ничего не бывает ... Кто же бродит опять у крыльца И по имени нас окликает?
Кто приник к ледяному стеклу И рукою, как веткою, машет?» (А. Ахматова).
Глава IV ОСНОВНЫЕ ЗАКОНЫ (ПРИНЦИПЫ) ПРАВИЛЬНОГО МЫШЛЕНИЯ
|
 Скачать 2.39 Mb.
Скачать 2.39 Mb.