Логика. Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики

• Название: Учебник по логике москва 2000 Оглавление Глава I. Предмет и значение логики Мышление как предмет изучения логики
• Анкор: Логика.doc
• Дата: 03.05.2018
• Размер: 2.39 Mb.
• Имя файла: Логика.doc
• Тип: Учебник; #18814
• страница: 23 из 25

§ 2. РАЗВИТИЕ ЛОГИКИ В СВЯЗИ С ПРОБЛЕМОЙ ОБОСНОВАНИЯ МАТЕМАТИКИ
Немецкий математик и логик Готтлоб Фреге (1848—1925) предпринял попытку свести математику к логике. С этой целью в первой своей работе по математической логике «Исчисление понятий» («BegnfTsschrift») он определил множество как объем понятия и таким образом получил возможность определить и чи­сло через объем понятия. Такое определение числа он сфор­мулировал в «Основаниях арифметики» («Grundlagen der Arithmetik»), книге, которая в то время осталась незамеченной, но впоследствии получила широкую известность. Здесь Фреге определяет число, принадлежащее понятию, как объем этого понятия. Два понятия считаются равночисленными, если множе­ства, выражающие их объемы, можно поставить во взаимоодноз­начное соответствие друг с другом. Так, например, понятие «вер­шина треугольника» равночисленно понятию «сторона треуголь­ника», и каждому из них принадлежит одно и то же число 3, являющееся объемом понятия «вершина треугольника».

Если Лейбниц только наметил программу сведения математи­ки к логике, то Г. Фреге предпринял попытку сведения довольно значительной части арифметики к логике, т. е. произвел некото­рую математизацию логики²². Символические обозначения, при­нятые им, очень громоздки и поэтому мало кто полностью прочитал его «Основные законы арифметики». Сам Фреге осо­бенно и не рассчитывал на то, что его произведение найдет читателей. Тем не менее труд Фреге сыграл значительную роль

в истории обоснования математики в первой половине XX в. В этом произведении Фреге писал: «В моих «Основаниях арифме­тики» (1884) я пытался привести аргументы в пользу того, что арифметика есть часть логики и не должна заимствовать ни у опыта, ни у созерцания никаких основ доказательства. В этой книге (речь идет об «Основных законах арифметики». — Л. Г.)это должно быть подтверждено тем, что простейшие законы арифме­тики здесь выводятся только с помощью логических средств» .

Итак, Фреге полагал, что он логически определил число и точ­но перечислил логические правила, с помощью которых можно определять новые понятия и доказывать теоремы, и что таким образом он и сделал арифметику частью логики. Фреге не подо­зревал, однако, что построенная им система не только не пред­ставляла собой логического обоснования содержательной ариф­метики, но была даже противоречивой. Это противоречие в си­стеме Фреге обнаружил Бертран Рассел.

В послесловии к «Основным законам арифметики» Фреге писал по этому поводу: «Вряд ли есть что-нибудь более нежела­тельное для автора научного произведения, чем обнаружение по завершении его работы, что одна из основ его здания оказывает­ся пошатнувшейся (опровергнутой: erschuttert). В такое положе­ние я попал, получив письмо от господина Бертрана Рассела, когда печатание этой книги близилось к концу»² . Противоречи­ем, которое обнаружил Рассел в системе Фреге, был знаменитый парадокс Рассела о множестве всех нормальных множеств (см. с. 193 -194).

Причину своей неудачи Фреге видел в использованном им предположении, что у всякого понятия есть объем в смысле постоянного, строго фиксированного множества, не содержащего в себе никакой неопределенности или расплывчатости. Ведь именно через этот объем он и определил основное понятие математики: понятие числа.

Вслед за Г. Фреге очередную попытку сведения математики к логике предпринял видный английский философ и логик Берт­ран Рассел (1872—1970). Он также автор ряда работ из области истории, литературы, педагогики, эстетики, естествознания, со­циологии и др. Труды Рассела в области математической логики оказали большое влияние на ее развитие. Вместе с английским логиком и математиком А. Уайтхедом²⁵ Рассел разработал ори­гинальную систему символической логики в фундаментальном трехтомном труде «Principia Mathematica»²⁶. Выдвигая идею о сведении математики к логике, Рассел считает, что если гипо­теза относится не к одной или нескольким частным вещам, но к любому предмету, то такие выводы составляют математику. Таким образом, он определяет математику как доктрину, в кото­рой мы никогда не знаем, о чем мы говорим, и не знаем, верно ли то, что мы говорим. Рассел делит математику на чистую и прикладную. Чистая математика, по его мнению, есть совокупность формальных вы­водов, независимых от какого бы то ни было содержания, т. е. это класс высказываний, которые выражены исключительно в те­рминах переменных и только логических констант. Рассел не только вполне уверен в том, что ему удалось свести математику к такого рода предложениям, но и делает из этого утверждения вывод о существовании априорного знания, считает, что «мате­матическое познание нуждается в посылках, которые не базиро­вались бы на данных чувства»²⁷. Отсюда видно, что Рассел разрывает две взаимосвязанные ступени познания — чувствен­ную и рациональную. Он отбрасывает в математике первую ступень познания и переходит сразу к абстрактному мышлению, а это и есть априоризм, стремление показать, что математические истины — истины разума, никак не связанные с опытом, с чувст­венным восприятием мира.

От чистой математики Рассел отличает прикладную матема­тику, которая состоит в применении формальных выводов к ма­териальным данным.

Для того чтобы показать, что чистая математика сводится к логике, Рассел берет систему аксиом арифметики, сформулиро­ванную Пеано, и пытается их логически доказать, а три неоп­ределяемых у Пеано понятия: «нуль», «число», «следующее за» — определить в терминах своей логической системы. Все натуральные числа Рассел также считает возможным выразить в терминах логики, а следовательно, свести арифметику к логике. А так как, по его мнению, вся чистая математика может быть сведена к арифметике, то и математика может быть сведена к логике. Рассел пишет: «Логика стала математической, матема­тика логической. Вследствие этого сегодня совершенно невоз­можно провести границу между ними. В сущности это одно и то же. Они различаются как мальчик и мужчина; логика — это юность математики, а математика — это зрелость логики»²⁸. Рассел считает, что не существует пункта, где можно было бы провести резкую границу, по одну сторону которой находилась бы логика, а по другую — математика.

Но в действительности математика несводима к логике. Пред­меты изучения этих наук различны. Нами ранее были указаны характерные черты, присущие логике как науке (см. с. 114). У математики другие задачи и функции.

В большом трехтомном труде «Principia Malhematica» есть две стороны. Первая — заставляющая видеть в нем один из основных истоков современной математической логики. Все, что связано с этой стороной Principia Mathematica, получило в даль­нейшем такое развитие в математической логике, которое сдела­ло эту новую область науки особенно важной для решения не только труднейших задач теоретической математики и ее обоснования, но и целого ряда весьма важных для практики задач вычислительной математики и техники.

Другая сторона этого произведения — точнее, даже не самого этого произведения, а философских «обобщений», делаемых логицистами со ссылкой на него, — принадлежит уже к области попыток использовать его для «доказательства» положения, что математика-де сводится к логике. Именно эта сторона и относит­ся к области неправильных выводов. Именно ее и опровергает дальнейшее развитие науки, которое обнаружило, что эта попыт­ка Рассела не удалась. И это не случайно. Дело не в том, что Рассел в каком-то смысле не совсем удачно построил свою систему. Дело в том, что и нельзя построить формальную «логи­ческую систему» с точно перечисленными и эффективно выпол­нимыми правилами вывода, в которой можно было бы фор­мализовать всю содержательную арифметику. Это обстоятельст­во представляет собой содержание известной теоремы австрийс­кого математика и логика К. Гёделя о неполноте формализован­ной арифметики, из которой следует непосредственно, что опре­деление математических понятий в терминах «логики» хотя и об­наруживает некоторые связи этих понятий с логикой, но не лишает их тем не менее специфически математического содержа­ния. Формализованная система имеет смысл лишь при наличии содержательной научной теории, систематизации которой данная формализованная система должна служить.

Однако Г. Фреге и Б. Рассел пришли в логическом анализе к ряду интересных результатов, относящихся к понятиям «пред­мет», «имя», «значение», «смысл», «функция», «отношение» и др. Особо следует подчеркнуть важность разработанной Расселом теории типов (простой и разветвленной), цель которой состоит в том, чтобы помочь разрешить парадоксы в теории множеств. Рациональное зерно разветвленной теории типов Рассела состоит в том, что она является конструктивной теорией.
§ 3. МНОГОЗНАЧНЫЕ ЛОГИКИ
Если в двузначной логике высказывание бывает истинным или ложным, то в многозначных логиках число значений истинности аргументов и функций может быть любым конечным и даже бесконечным. В настоящем приложении отрицание обозначается через Nxили

конъюнкция — через Кху илинестрогая дизъюнкция —через Аху илиматериальная импликация — через Сху илиЗначения функции от аргумента а будем записывать так: [д]. Тавтологией (или общезначимой) называется формула, которая при любых комбинациях значений входящих в нее переменных принимает значение «истина» (чаще всего в рас­сматриваемых системах «истина» обозначается цифрой 1).

Развитие многозначных логик, по нашему мнению, подтверждает мысль, что истина всегда конкретна, а также положение об относительном характере конкретно-научных знаний: то, что яв­ляется тождественно-истинным в одной логической системе, не оказывается тождественно-истинным в другой.

Трехзначная система Лукасевича²⁹

Трехзначная пропозициональная логика была построена Я. Лукасевичем в 1920 г. В ней «истина» обозначается 1, «ложь» — 0, «нейтрально» — ¹/₂ . В качестве основных функций взяты отрицание (обозначается Nx) и импликация (Сху); произ­водными являются конъюнкция (Кху) и дизъюнкция (Аху). Тав­тология принимает значение 1.

Отрицание и импликация соответственно определяются мат­рицами (табл. 13, 14) и равенствами так:
_{Таблица 13}

х	Nx
1 ½ 0	0 ½ 1

Таблица 14

х / у	1	1/2	0
1 ½ 0	1 1 1	½ 1 1	0 ½ 1

1) [Nx]=l-[x];2) [Сху] = 1, если; 3) [Сху] = 1-[x]+[у], если [x]>[у], или в общем виде: 4)[Сху]=min (1,1 — [x]+[у]).

Конъюнкция определяется как минимум значений аргумен­тов: [Kxy]=min ([x], [у]); дизъюнкция — как максимум значений х и у: [Аху]= тах ([x], [у]).

На основе данных определений отрицания, конъюнкции и ди­зъюнкции в системе Лукасевича не будут тавтологиями (закона­ми логики) закон непротиворечия и закон исключенного третьего двузначной логики, а также и отрицания законов непротиворечия и исключенного третьего. Поэтому логика Лукасевича не являет­ся отрицанием двузначной логики. В логике Лукасевича тавтоло­гиями являются правило снятия двойного отрицания, все четыре правила де Моргана и правило контрапозиции: Не являются тавтологиями правила приведения к абсурдудвузнач­ной логики: и (т. е. если из х вытекает противоречие, то из этого следует отрицание х).Это можно доказать, взяв [х] = ¹/₂ и [у] = ¹/₂ .

В системе Лукасевича не являются тавтологиями и некоторые формулы, структурно выражающие правильные дедуктивные умозаключения традиционной логики, формализованные средст­вами алгебры логики, а именно modus tollens, простая деструк­тивная дилемма, а также формулы разделительно-категоричес­кого силлогизма с нестрогой дизъюнкцией.

Все тавтологии логики Лукасевича являются тавтологиями в двузначной логике, ибо если отбросить значение ¹/₂, то в логике Лукасевича и в двузначной логике определения фу­нкций конъюнкции, дизъюнкции, импликации и отрицания соответственно совпадут. Но так как в логике Лукасевича имеется третье значение истинности — ¹/₂ , то не все тавтологии двузначной логики являются тавтологиями в логике Лука­севича.
Трехзначная система Рейтинга

В двузначной логике из закона исключенного третьего выво­дятся: 1)2)Исходя из утверждения, что истинным является лишь второе, Гейтинг разработал трехзначную пропо­зициональную логику. В этой логической системе импликация и отрицание отличаются от определений этих операций у Лукасе­вича лишь в одном случае. «Истина» обозначается 1, «ложь» — 0, «неопределенность» — ¹/₂. Тавтология принимает значение

1 (табл. 15, 16).

Таблица 15

Отрицание Гейтинга

х	Nх
1 ½ 0	0 0 1

Таблица 16

Импликация Гейтинга

х /у	1	1/2	0
1 ½ 0	1 1 1	½ 1 1	0 0 1

1) [Сху]=1 ,если

2) [Сху] = [у],если

Конъюнкция и дизъюнкция определены обычным способом как минимум и максимум значений аргументов.

Если учитывать лишь значения функций 1 и 0, то из матриц системы Гейтинга вычленяются матрицы двузначной логики. В этой трехзначной логике закон непротиворечия является тавто­логией, но ни закон исключенного третьего, ни его отрицание тавтологиями не являются. Оба правильных модуса условно-категорического силлогизма, формулаправила де Моргана и закон исключенного четвертого: — тавто­логии.

Хотя по сравнению с логикой Лукасевича в матрицах отрица­ния и импликации Гейтингом в его системе были произведены небольшие изменения, результаты оказались значительными: в системе Гейтинга являются тавтологиями многие формулы классического двузначного исчисления высказываний.
Трехзначная система Бочвара³⁰

Система советского логика Д. А. Бочвара построена на раз­делении высказываний на имеющие смысл (т. е. истинные или ложные) и бессмысленные. Бочвар выделяет внешние формы (или функции) и внутренние. Внутренние формы Бочвар называет классическими содержательными функциями переменных выска­зываний, а внешние формы — не классы чески ми. У Бочвара «ис­тина» обозначается Л, «ложь» — F, «бессмысленность» — S. Мы обозначим «истину» как 1, «ложь» — 3, «бессмысленность» — 2. Тавтология принимает значение 1; а, Ь, с... обозначают перемен­ные высказывания.

В настоящей работе не приводится полное определение функ­ций (в силу его сложности). Бочвар ввел два вида отрицания — внутреннее и внешнее, которые определяются таблично,— внутреннее отрицание, — внешнее отрицание,— внутрен­нее отрицание внешнего утверждения.

В системе Бочвара ни закон тождества двузначной логики, ни его отрицание не являются тавтологиями. Отрицание закона тождества сыграло важную роль при анализе парадокса Рассела. Бочвар же не отбрасывает принцип «а есть а» илив его системе формулане является доказуемой.

Противоречиями в логике Бочвара являются следующие формулы: 1)2)3)Здесь знакозначает внешнюю равнозначность (эквивалентность), знак— внеш­нюю равносильность.

Бочвар построил свое трехзначное нечисление с целью разрешения парадоксов классической математической логики методом формального доказательства бессмысленности опре­деленных высказываний. В частности, с помощью своей системы Бочвар смог разрешить парадокс Рассела о множестве всех нормальных множеств, доказав несуществование такого предмета, как множество всех нормальных множеств. В дей­ствительности это означает, что, поскольку предметная область состоит из фиксированных предметов, о которых можно рассуждать по законам классической формальной логики, множество всех нормальных множеств нельзя рас­сматривать как фиксированный предмет, не изменяющийся в то время, пока о нем идет речь. Система Бочвара позволяет элиминировать парадокс Рассела, не прибегая к теории типов.
n-значная система Поста³¹

Система Поста является обобщением двузначной логики, ибо при л=2 в качестве частного случая мы получаем двузначную логику. Своей системе Пост дал интерпретацию. Значения истин­ности суть 1, 2,..., лгде л — конечное число. Тавтологией является формула, которая всегда принимает такое значение i, что где значения 1, ..., Sназываются выделенными или отмеченными; возможно, что

Пост вводит два вида отрицания (N*xи N¹x)_yсоответственно называемые циклическим и симметричным. Они определяются путем матриц и посредством равенств.

Первое отрицание определяется двумя равенствами:

1. LY¹x]=M+l при

2. [^п]=1.

Второе отрицание определяется одним равенством:

[N²x]=n-[x] + \.

Матрица, определяющая первое и второе отрицания, имеет вид табл. 17.
Таблица 17

x	N 2x	N 2x
1 2 3 4 . . . n -1 n	2 3 4 5 . . . n 1	n n -1 n -2 n -3 . . . 2 1

Характерной особенностью двух отрицаний Поста является то, что при л=2 эти отрицания совпадают между собой и с от­рицанием двузначной логики, что подтверждает тезис: много­значная система Поста есть обобщение двузначной логики.

Конъюнкция и дизъюнкция определяются соответственно как максимум и минимум значений аргументов. При указанных опре­делениях отрицания, конъюнкции и дизъюнкции обнаруживается, что при значении для х, большем двух, законы непротиворечия и исключенного третьего, а также отрицания этих законов не являются тавтологиями.

Если значениями истинности являются 1, 2, 3, то из n -значной системы Поста вычленяется трехзначная логика, т. е. Р_ъ. Анало­гично при значениях истинности 1, 2, 3, 4 получается четырех­значная логика Р₄и т. д.

Трехзначная система Р₃ Поста имеет следующую форму (табл. 18, 19).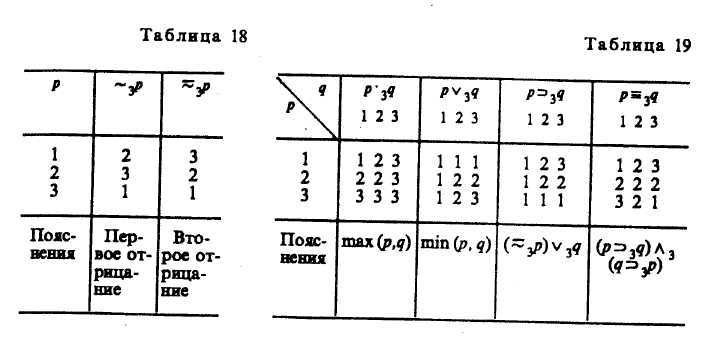


В этих таблицах приняты обозначения, введенные Постом приn-3:первое отрицание обозначается черезвторое отрицание — черезконъюнкция — через дизъюнкция — через импликация — через эквиваленция — через

Если в качестве значений истинности взяты лишь 1 «истина» и 3 «ложь», то из таблиц системы Р₃ Поста вычленяются таблицы для отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции двузначной логики.

В системе Р_этавтология принимает значение 1; закон ис­ключенного третьего не является тавтологией ни для первого, ни для второго отрицания Поста, но является тавтологией закон исключенного четвертого для первого отрицания.
Трехзначная система Рейхенбаха³²

Аппарат многозначных логик находит все более широкое применение в различных науках. Проанализируем применение аппарата трехзначной логики Г. Рейхенбаха к квантовой меха­нике.

Большинство операций этой системы было введено уже По­стом, но с целью приложения своей системы к квантовой меха­нике Рейхенбах вводит новые. У Поста было введено два вида отрицания — первое и второе. В системе Рейхенбаха они называ­ются циклическим отрицанием и диаметральным отрицанием, кроме них Рейхенбах ввел полное отрицание. В системе Рейхен­баха имеются стандартная импликацияи стандартная эк­вивалентностьВводятся и другие операции: альтернативная импликация, квазиимпликацияи альтернативная эквива­лентностьЗнаком «•» обозначена конъюнкция, —ди­зъюнкция.

Таблица для трех видов отрицаний Рейхенбаха. Обозначения:

— циклическое отрицание; — А — диаметральное отрица­ние;— полное отрицание.

Рейхенбах обозначил «истину» как 1, «неопределенность» — 2, «ложность» — 3. Тавтология принимает значение 1 (табл. 20).

Таблица 20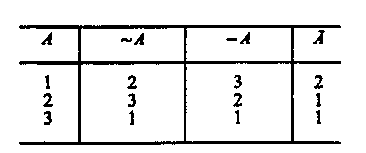



Другие функции Рейхенбаха определяются матрицами так (табл. 21).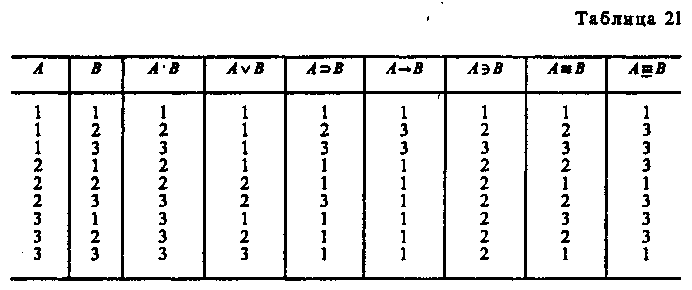



Отметим ряд свойств, присущих отрицаниям в системе Рей­хенбаха.

Для циклического отрицания верен закон снятия тройного отрицания: т. е. в результате тройного отрицания

А возвращаемся к исходному значению А. Для циклического отрицания законы непротиворечия и исключенного третьего, пра­вила де Моргана двузначной логики не являются тавтологиями, но тавтологией является закон исключенного четвертого:

Для диаметрального отрицания сохраняется правило снятия двойного отрицания:Ни сами законы непротиворечия и исключенного третьего, ни их отрицания при диаметраль­ном отрицании не являются тавтологиями.

Для полного отрицания оказались тавтологиями закон непро­тиворечия, псевдозакон исключенного третьего, закон исключен­ного четвертого, правила де Моргана, закон

Рассмотрев три вида отрицания в их взаимосвязи, Рейхенбахпоказал, что между циклическим и полным отрицанием имеет место следующее отношение:

(1)

Ранее отмечалось, что для циклического отрицания является тавтологией закон исключенного четвертого: Последние два члена его можно заменить на основании равенства (1) на и получить для полного отрицания формулу которую Рейхенбах назвал «псевдозаконом исключенного третье­го», ибо он не имеет свойств закона исключенного третьего двузначной логики. Причина последнего в том, что полное от­рицание не имеет свойств обычного отрицания: оно не дает нам возможности определить значение истинности А, если мы знаем, что истинно. Из табл. 22, определяющей полное отрицание, следует, что еслиистинно, то А может быть как ложным, так и неопределенным.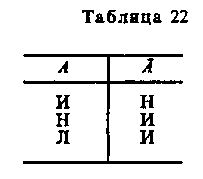



Вследствие этой двусмысленности для полного отрицания нельзя определить обратной операции, т. е. операции, ведущей отк А.

Взаимосвязь трех видов отрицания выражается в том, что закон непротиворечия сохраняется в таких трех формах:

1)

Рейхенбах построил свою трехзначную систему для описания явлений квантовой механики. По его мнению, говорить об истин­ности или ложности высказываний правомерно лишь тогда, ког­да возможно осуществить их проверку. Если нельзя ни подтвер­дить истинность Высказывания (т. е. верифицировать его), ни опровергнуть его с помощью проверки (фальсифицировать), то такое высказывание должно оцениваться третьим значением — неопределенно. К числу таких высказываний относятся высказы­вания о ненаблюдаемых объектах в микромире.

Сам Рейхенбах так пишет о значении трехзначной логики для квантовой механики: «Введение третьего значения истинности не делает все высказывания квантовой механики трехзначными. Рамки трехзначной логики достаточно широки, чтобы включать класс истинно-ложных формул. Когда мы хотим все высказывания квантовой механики ввести в состав трехзначной логики, то руководящей идеей будет: поместить в истинно-ложный класс те высказывания, которые мы называем законами квантовой меха­ники»³³.
Бесконечнозначная логика как обобщение многозначной системы Поста

Исходя из системы Р_щПоста, мы (А. Г.) строим бесконечнозначную систему G_х0. Значениями истинности являются 1 (ис­тина), 0 (ложь) и все дробные числа в интервале от 1 до 0,построенные в форме

и в форме где к — целочисленный показатель.
Это числа: 1, ½, ¼, ¾, 1/8, 7/8, 1/16, 15/16, …,
Операции: отрицание, дизъюнкция, импликация и эквиваленция в G_х0— определены следующими равенствами:

1. Отрицание:

2. Дизъюнкция:

3. Конъюнкция:

4. Импликация:

5. Эквиваленция:

Отрицание в системе G_х0является обобщением второго (сим­метричного) отрицания n-значной логики Поста. Посредством именно второго отрицания строятся конъюнкция, импликация и эквиваленция в системе G_х0. Система G_х0построенная пред­ложенным способом, имеет множество тавтологий³⁴. Тавтологи­ей, например, является формула, гласящая, что отрицание р, повторенное два раза, даст первоначальное значение Тавтологиями в G_х0будут четыре правила де Моргана.

Тавтологии в G_х0являются тавтологиями в двузначной ло­гике, ибо бесконечнозначная система G_х0является обобщением системы Р_яПоста, а последняя есть обобщение двузначной логики.

Для проверки правильности построения G_х0предложенным нами способом на основании системы G_х0построили систему G_3, взяв в качестве значений истинности 1, 1\2, 0. Система G₃ совпадает с системой Р₃Поста. Из системы G_х0также вычленяется 4-значная система G₄, значениями истинности аргументов которой являются 1, ½, ¼, 0, а значениями истинности функции: 1, ½, ¼, ¾, 0.

Отрицание определяется по формуле

Конъюнкция, дизъюнкция, импликация, эквиваленция в G₄опре­делены табл. 23.

Таблица 23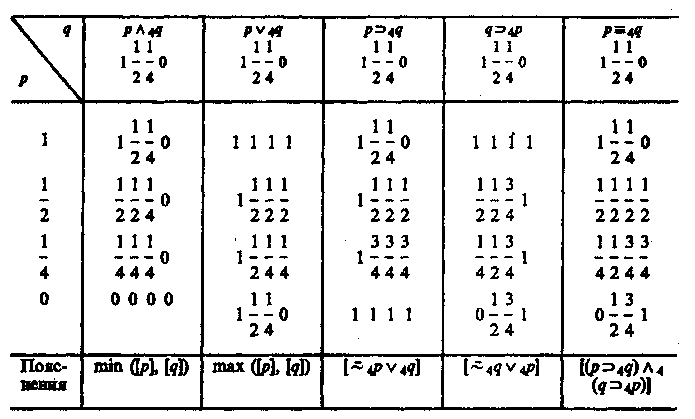



В 4-значной системе G₄содержится классическая двузначная логика [при значениях истинности 1 («истина») и 0 («ложь»)], а также система Р₃Поста (при значениях истинности 1, 1/2, 0).

Аналогично из G_х0вычленяется система G₅ ,а также G₆,,G₇ G₈и т. д.
Об интерпретации системы G_х0

В системе G_х0 между крайними значениями истинности — 1

(«истина») и 0 («ложь») лежит бесконечное число значений истин­ности: ¹/₂ ,¹/₄, ³/₄, ¹/₈, ⁷/₈ и т. д. Процесс познания осуществляется

таким образом, что мы идем от незнания к знанию, от непо­лного, неточного знания к более полному и более точному, от относительной истины к абсолютной. Абсолютная истина (в узком смысле) складывается из бесконечной суммы относитель­ных истин. Если значению истинности, равному 1, придать семан­тический смысл абсолютной истины, а значению 0 — значение лжи (заблуждения, отсутствия знания), то промежуточные значе­ния истинности отразят процесс достижения абсолютной истины как бесконечный процесс, складывающийся из познания относи­тельных истин, значениями которых в системе G_х0являются ¹/₂ , ¼, ¾, ¹/₈, ⁷/₈... — и т. д. Чем ближе значение истинности перемен­ных (выражающих суждения) к 1, тем большая степень приближе­ния к абсолютной истине. Так осуществляется процесс познания от незнания к знанию, от явления к сущности, от сущности первого порядка к сущности второго порядка и т. д. Этот бес­конечный процесс познания и отражает бесконечнозначная систе­ма G_х0, построенная нами как обобщение двузначной классичес­кой логики, характеризующей процесс познания в рамках опери­рования предельными значениями истинности суждений — исти­на и ложь. Такова семантическая интерпретация бесконечнозначной системы G_х0раскрывающая ее роль в процессе познания истины.