Учебник Под редакцией доктора экономических наук, профессора Л. А. Каргиной

• Название: Учебник Под редакцией доктора экономических наук, профессора Л. А. Каргиной
• Дата: 20.08.2022
• Размер: 4.86 Mb.
• Имя файла: Cifrovaya_ekonomika_RUT.docx
• Тип: Учебник; #649499
• страница: 15 из 27

l

1

l
_( y_i

i1

l


_y) ^.
2

i

i1

физике или теории информации), в частности непред- сказуемости появления какого-либо символа алфавита. В последнем случае уровень энтропии численно равен количеству информации на символ передаваемого сооб- щения. [25]

Функция энтропии Шеннона имеет вид:


n




H _p_ilog₂ p_i,

i1

где p_i— это вероятность нахождения системы в i-ом состо- янии. Следует отметить, что чем выше уровень энтропии H, тем ниже уровень упорядоченности в системе. Таким образом, перед аналитическими алгоритмами ставится задача минимизации функции энтропии.

Таким образом, алгоритм построения дерева решений при решении задачи регрессии будет выполняться до того момента, пока в каждой из подвыборок не окажутся объ- екты со значением целевой переменной в допустимом диапазоне.
Пример расчёта уровня энтропии системы и построения дерева решений

Построим дерево решений (рис. 3.8).

KNN(Методkближайшихсоседей)

Метод k ближайших соседей — это алгоритм, который применяется в решении задач классификации и регрес- сии. KNN основывается на гипотезе компактности.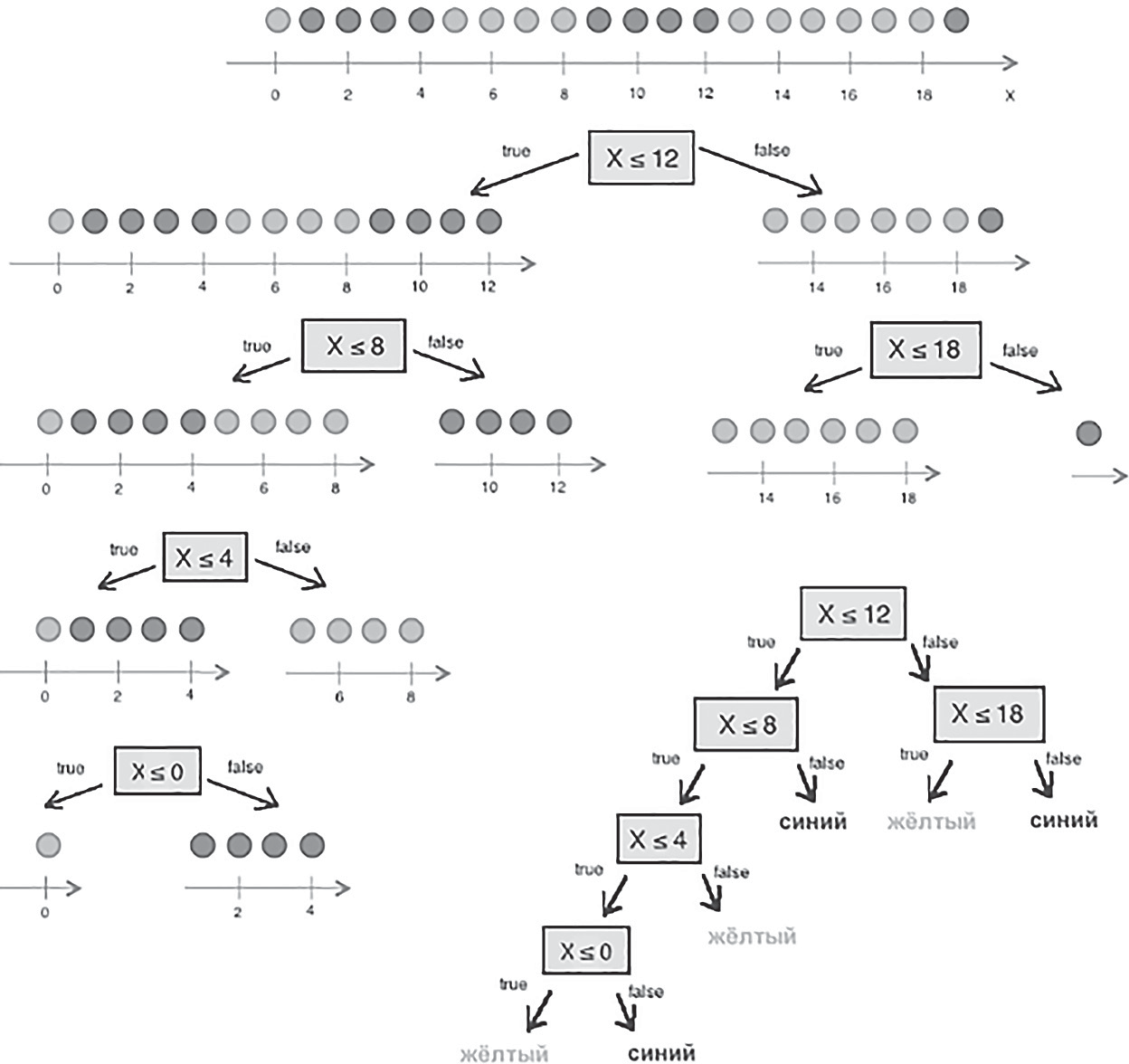

Пусть на множестве объектов задана функция рас- ^{стояния p}^x,xm ^{. Задачей этой функции является ото-} бражение степени сходства/различия между объектами

выборки. Таким образом, значение функции расстояния между объектами обратно пропорционально степени схо- жести объектов выборки.

Первым этапом реализации метода ближайших сосе- дей является выбор адекватной задаче метрики рассто- яния и расчёт расстояний между объектами выборки. Для расчёта меры расстояния между объектами выборки используют следующие метрики: евклидово расстояние, квадрат евклидова расстояния, манхэттенское расстоя- ние, степенное расстояние и др.

^{Евклидово расстояние d} ^p,q <sup>для точек p  p1,, pn

и q</sup> ^q1,,qn <sup>рассчитывается по формуле:

d</sup> ^p,q ^
Квадрат евклидова расстояния:

n

^d ^p,q ^ _^{( p q)2}

k k

k1
Манхэттенское расстояние:

Риc. 3.8.Дереворешений

^d ^p,q ^ _
p q

Гипотеза компактности — это предположение о том, что схожие объекты гораздо чаще лежат в одном классе, чем в разных; или, другими словами, что классы обра-
Степенное расстояние:

k k


n
k1


k k
n ¹

зуют компактно локализованные подмножества в про- странстве объектов. Из вышесказанного также можно сделать вывод, что граница между классами имеет доста- точно простую форму. [26]

Пусть задана обучающая выборка пар «объект-ответ»


^d ^p,q ^{ (}_^{| p q|b)r}k1

где b и r это параметры настройки модели, определяемые пользователем.

После выбора метрики и расчёта расстояний необ-

X^m_x₁,y₁ ,,(x

,y_

ходимо отсортировать объекты выборки по возрастанию

^mmзначения функции расстояния

^p^x,xm ^{до классифициру-}

емого объекта. Таким образом, алгоритм классификации KNN включает в себя следующие шаги:

• 
  нормализация данных;
  
• 
  вычисление расстояний между объектами выборки;
  
• 
  сортировка объектов выборки по убыванию значе- ния функции расстояния ^p^x,xm;
  
• 
  присвоение анализируемому объекту класс, наибо- лее часто встречающийся среди k соседей.
  

Одним из механизмов настройки работы алгоритма классификации KNN является перебор параметра k (коли- чество k соседей). При k = 1 алгоритм ближайшего соседа является неустойчивым к шумовым выбросам. [27] При k = m, степень устойчивости предельно растет и резуль- тат работы алгоритма превращается в константу. Учиты- вая вышеперечисленное, можно сделать вывод о том, что оптимальное значение параметра k отличается от край- них значений k = 1 и k = m, где m количество элементов выборки. Для подбора оптимального параметра k исполь- зуют алгоритм кросс-валидации.

Кросс-валидация — это группа методов оценки качества предиктивной модели, которые основываются на перекрест- ном разбиении первичной выборки на обучающие и тесто- вые наборы данных и получении усредненного результата по всем случаям разбиения. Схема перекрестного разбиения набора данных представлена на рисунке 3.9.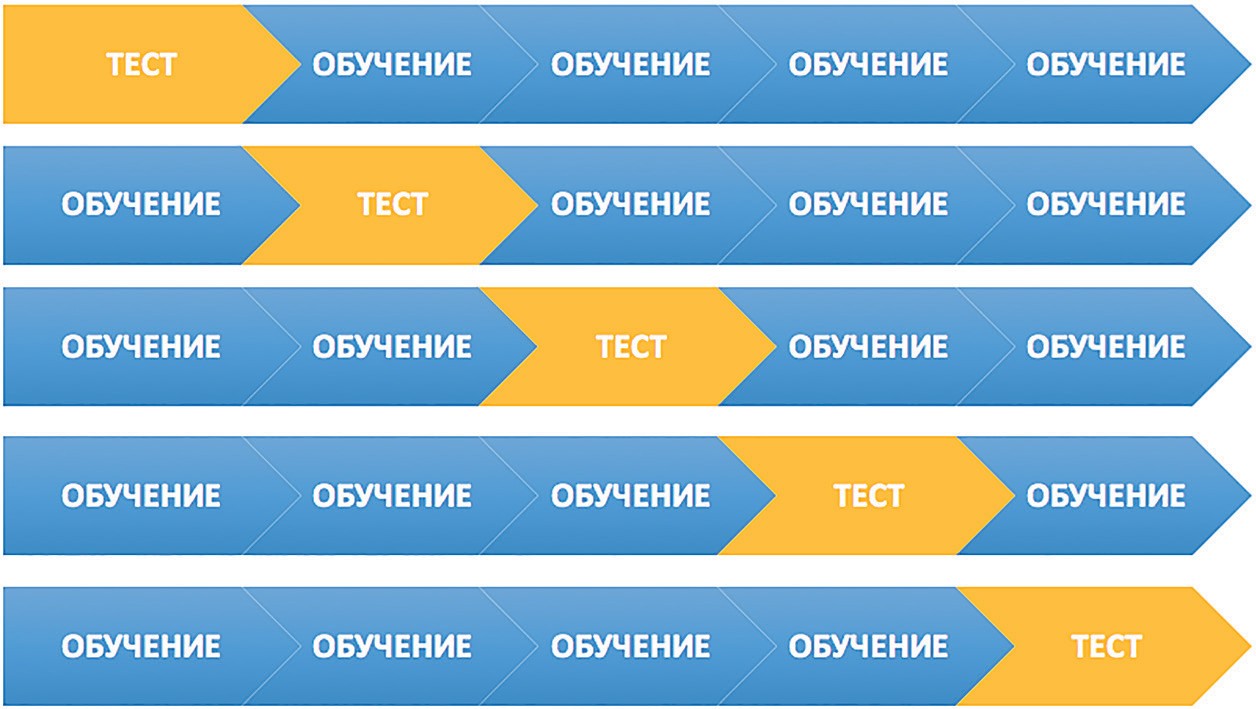




Рис3.9.Схемакросс-валидации

Кросс-валидация позволяет осуществлять более взве- шенный выбор архитектуры модели анализа данных, однако является ресурсоемкой операцией, сложность которой резко возрастает с увеличением объема, анали- зируемых данных.

Нормализация данных является необходимым этапом подготовки данных в тех случаях, когда поля различных признаков содержат данные в разных единицах измерения. Если не производить нормализацию данных, признаки, значения которых находятся в диапазоне от 0 до 100, ока- жут большее влияние на целевую переменную, чем при- знаки, значения которых находятся в диапазоне от 0 до 10. Нормализация величины ^xjпроизводится по формуле:


x  x

j
_x^xj ^{ x}min _.

max min

Результатом нормализации является набор данных, значения признаков которого варьируются в диапазоне от 0 до 1 и таким образом содержит относительные вели- чины вместо абсолютных. Вышеописанная операция позволяет нивелировать влияние признаков.

Пример нормализации данных и классификации нового наблюдения методом kближайших соседей.

В таблице представлен классифицированный (раз-

меченный) набор данных о наблюдениях, собранных по двум признакам, значения которых варьируются от 0 до 1000 для первого признака и от 0 до 10 для второго. Проведем классификацию Наблюдения 19 со значениями признаков:

Признак 1 — 90

Признак 2 — 1,3

Наблюдение №	Признак 1	Признак 2	Класс
1	100	0,9	1
2	80	1,1	1

Окончаниетаблицы

Наблюдение №	Признак 1	Признак 2	Класс
3	80	0,9	1
4	180	0,8	3
5	80	1,6	2
6	170	1	3
7	180	1,1	3
8	160	1,1	3
9	70	0,8	1
10	100	1,4	2
11	90	1,5	2
12	110	1,7	2
13	60	1	1
14	190	1	3
15	180	0,9	3
16	80	0,7	1
17	100	1,6	2
18	110	1,5

Шаг 1. Нормализация данных

Произведем нормализацию набора данных, после чего значения признаков будут варьироваться в диапазоне от 0 до 1 и таким образом содержать относительные величины вместо абсолютных.

Нормализация значений признаков наблюдения 1:

Нормализация признака 1:

_{X1 }1000 _{ 0,1}

¹ 1000  0

Нормализация признака 2:

Нормализованные значения признаков запишем в таблицу:

Наблюдение №	Признак 1	Признак 2	Класс
1	0,1	0,09	1
2	0,08	0,11	1
3	0,08	0,09	1
4	0,18	0,08	3
5	0,08	0,16	2
6	0,17	0,1	3
7	0,18	0,11	3
8	0,16	0,11	3
9	0,07	0,08	1
10	0,1	0,14	2
11	0,9	0,15	2
12	0,11	0,17	2
13	0,06	0,1	1
14	0,19	0,1	3
15	0,18	0,09	3
16	0,08	0,07	1
17	0,1	0,16	2
18	0,11	0,15	2

Шаг 2. Нормализация значений признаков нового наблюдения

Произведем нормализацию значений признаков нового наблюдения согласно их диапазонам.

Нормализация значений признаков наблюдения 19:

Нормализация признака 1:

X²  ^0,90  0,09 <sup>X1 900  0,09

1</sup> 10  0 ^{19 1000  0}

Нормализация признака 2:

Окончаниетаблицы

X

Наблюдение №	Класс	Расстояние
15	3	0,0985
4	3	0,103
14	3	0,1044
11	2	0,8102

²  ^1,30  0,13

¹⁹ 10  0

Шаг 3. Сортировка объектов выборки по убыванию значения функции расстояния

Ниже приведён расчёт расстояния между Наблюде- нием 1 и Наблюдением 19:

^d^1,19 ^{ =}

= 0,0412310562561766.

Рассчитаем расстояния до других наблюдений и запи- шем их в таблицу, округлив до 4-х знаков после запятой, а затем отсортируем получившийся массив по возраста- нию расстояния до классифицируемого наблюдения:

Наблюдение №	Класс	Расстояние
10	2	0,0141
2	1	0,0224
18	2	0,0283
5	2	0,0316
17	2	0,0316
1	1	0,0412
3	1	0,0412
13	1	0,0424
12	2	0,0447
9	1	0,0539
16	1	0,0608
8	3	0,0728
6	3	0,0854
7	3	0,0922

Шаг 4. Определение числа k соседей

На этом шаге необходимо выбрать число соседей и определить, к какому классу принадлежит большинство из них.

Если k = 1, то ближайшим соседом будет Наблюдение 10 и результатом классификации будет Класс 2.

Если k = 2, то Наблюдение 19 будет классифициро- вано в Класс 2 и Класс 1 с равной долей вероятности.

При k = 4 результатом классификации является Класс 2. Таким образом, очевидно, что результат классифика- ции сильно зависит от значения параметра k. При выборе слишком малого значения kприсутствует риск того, что ближайшими соседями классифицируемого наблюдения окажутся выбросы. В таком случае результат класси- фикации окажется неверным. Существует возможность минимизировать подобный риск ограниченным уве- личением числа соседей. В случае, когда выбрано мак- симальное количество соседей k= N, где Nэто общее количество наблюдений выборки, классифицируемому объекту будет присваиваться наиболее часто встречаю- щийся класс, результат алгоритма превратится в кон- станту для данной выборки. Обычно значение параметра k может варьироваться от 3 до 10 и часто оказывается близким к квадратному корню от числа всех наблюдений выборки. [28] Оптимизация числа соседей достигается перебором значений параметра kна тестовых выборках

при кросс-валидации.

Метрикикачества

Для сравнения эффективности применения различ- ных алгоритмов машинного обучения существует необ- ходимость определения метрики качества, которые могут выступить в качестве индекса производительности Pдля задач класса T. [21]

Классическими метриками качества для задач регрес- сии являются средняя абсолютная (Mean Absolute Error, MAE) и средняя квадратичная ошибки (Mean Squared Error, MSE).

FP — False Positive — доля ложных прогнозов «лож- ная тревога»;

FN — False Negative — доля случаев, при которых модель проигнорировала объекты, действительно относя- щиеся к искомому классу «пропуск цели».

Точность (Preceision)

Preceision ^TP

TP  FP

Точностью работы алгоритма в данном случае явля- ется доля правильно классифицированных объектов


MAE ¹ l

^li1

₁ l

_ax  y_2

i i
2

выборки от общего числа случаев классификации.

Полнота (Recall)

Recall  ^TP

l
^MSE _ ^a^xi ^{ yi}

i1

Описание метрик качества для задач классификации требует представления следующей концепции для опи- сания этих метрик в терминах ошибок классификации, которые в англоязычной литературе именуютcя как confusion matrix (матрица неточностей). Рассмотрим при- мер: допустим, что у нас есть два класса и алгоритм, пред- сказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом [26]:

TP  FN

Полнотой работы алгоритма является доля правильно классифицированных объектов выборки от общего числа объектов, действительно находящихся в целевом классе.

F-мера (F-measure)

_{F  measure } 2*Preceision*Recall

Preceision  Recall

F-мера является гармоническим средним показателей точности и полноты.

Accuracy

	y= 1	y= 0
ŷ= 1	True Positive (TP)	False Positive (FP)
ŷ= 0	False Negative (FN)	True Negative (TN)

Здесь ŷ— это ответ алгоритма для данного объекта, а y— истинная метка класса на этом объекте;

TP — True Positive — доля правильных прогнозов

«попадание»;

TN — True Negative — доля случаев, при которых модель разумно проигнорировала объекты выборки;

Accuracy  ^TPTN

TP  TN  FP  FN

Мера Accuracy представляет собой консолидирован- ный показатель точности работы модели по всем классам.
Пример расчета качества работы алгоритма классификации

Пусть из 10100 единиц эксплуатируемого оборудова- ния откажет 100 единиц и есть алгоритм, правильно пред- сказывающий 90 отказов. Построим матрицу неточностей:

	Факт: откажет	Факт: не откажет
Прогноз: откажет	90	30
Прогноз: не откажет	30	9950

Точность (Preceision)

Preceision ⁹⁰  0,9

90  30

Полнота (Recall)

Recall ⁹⁰  0,9

90  30

F-мера (F-measure)

F  measure  ^2*0,9*0,9  0,9

0,9  0,9

Accuracy

Accuracy ^909950  0,95

90  9950  30  30