Учебник Под редакцией доктора экономических наук, профессора Л. А. Каргиной
 Скачать 4.86 Mb. Скачать 4.86 Mb.
|
Решение задач машинного обученияЗадача классификации сводится к распределению объектов выборки по n категориям на основании набора признаков. Следует отметить, что множество объектов, классовая принадлежность которых заранее известна, называется обучающей выборкой. Решением задачи клас- сификации называют построение алгоритма, способного классифицировать произвольный объект на основании множества признаков, классовая принадлежность кото- рого заранее неизвестна. Примером задачи классифика- ции может служить категоризация набора данных видов растений и животных на основании знаний, извлеченных из обучающей выборки. Задача регрессии представляет собой прогнозирова- ние некоторого числового значения, на основании набора признаков. Перед алгоритмом ставится задача построе- ния функции f: Rn R. Принципиальное отличие этого класса задач от задачи классификации заключается в типе прогнозируемой переменной. Примерами задач регрессии являются прогнозирование цен акций на бирже ценных бумаг и прогнозирование выручки торговой точки в сле- дующем периоде. Задача кластеризации представляет собой распре- деление объектов выборки на основании набора призна- ков по n категориям, которые ранее не были определены. При решении задачи кластеризации алгоритм обраба- тывает неразмеченный набор данных, разбивая выборку на непересекающиеся группы (кластеры). Примером задачи кластеризации может служить категоризация потребителей по степени заинтересованности группами товаров. Задача выявления аномалий сводится к просмо- тру набора признаков, описывающих объекты выборки на предмет выявления нетипичного значения/сочетания значений одного или нескольких признаков. Примером задачи выявления аномалий являются задачи связанные с мониторингом состояния оборудования, подозритель- ной активности, связанной с нетипичными финансовыми операциями банковского счета. Уменьшение размерности — это уменьшение числа признаков, описывающих объекты выборки. Согласно литературным данным, в некоторых случаях анализ дан- ных, такой как регрессия или классификация, может быть осуществлён в редуцированном пространстве более точно, чем в исходном пространстве. [24] Для решения вышеперечисленных задач применя- ются различные аналитические алгоритмы: Деревья при- нятия решений, случайный лес, KNN (метод k ближай- ших соседей), линейная и логистическая регрессии, метод опорных векторов, PCA (метод главных компонент), ICA (анализ независимых компонент), сингулярное разложе- ние, CART и многие другие. Методымашинногообучения«сучителем» Алгоритмы машинного обучения «с учителем» решают аналитические задачи, которые подразумевают необходимость наличия обучающей выборки. Обучающей выборкой в данном случае является размеченный набора данных, для которого заранее известна целевая перемен- ная (прогнозируемый параметр). Задача обучения «с учи- телем» сводится к задаче ассоциации некоторого «ввода» с некоторыми вариантами «вывода». Примером такой задачи может служить задача построения модели класси- фикации растений, обученной на основании обучающей выборки, в которой каждый случай измерений заранее ассоциирован с конкретным видом растения. Методымашинногообучения«безучителя» Алгоритмы машинного обучения «без учителя» решают аналитические задачи, связанные с изучением структуры и свойств собранного набора данных. Такой набор данных является неразмеченным, другими сло- вами, в нем отсутствуют данные о целевой переменной. Деревьяпринятиярешений Деревья принятия решений представляют собой логи- ческие схемы, которые позволяют получить конечный результат классификации объекта с помощью набора отве- тов на иерархически организованную систему вопросов. Структура дерева решений содержит 2 класса объектов: листья и ветви. Листья дерева решений содержат в себе условия для значений переменных, описывающих отдель- ный объект классификации. Листья дерева решений могут быть внутренними и терминальными. Внутренние вер- шины содержат предикаты, позволяющие направить объ- ект классификации по соответствующей ветви. Терми- нальные вершины содержат в себе конечную метку класса. Пример решающего дерева представлен на риc. 3.7. 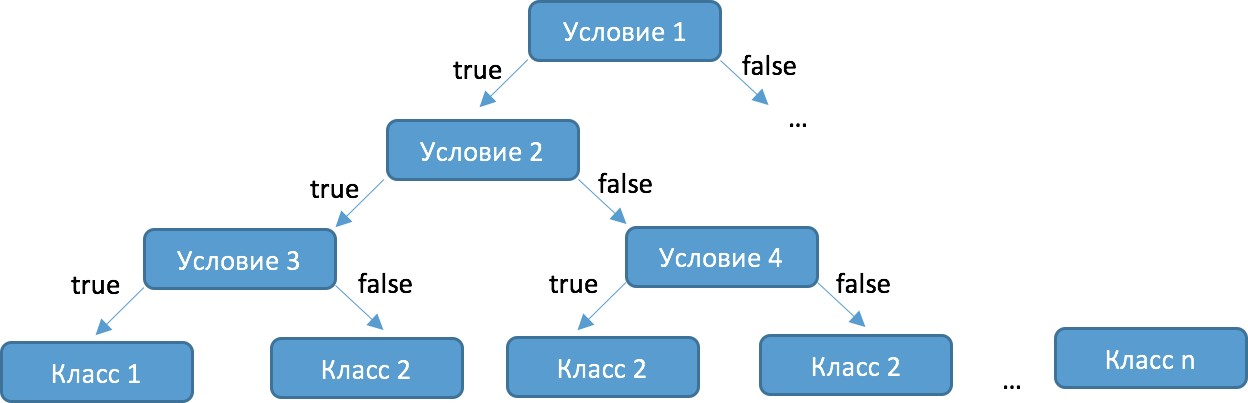 При прогнозировании качественного признака (задача классификации) алгоритм построения дерева решений включает в себя следующие шаги: расчёт уровня энтропии исходной выборки; перебор возможных условий первого листа дерева решений (для каждого элемента выборки необходимо перебрать все его атрибуты и сгенерировать предикат, способный разделить выборку); расчёт нового уровня энтропии системы при разде- лении выборки на основании каждого предиката; выбор предиката, при котором будет наблюдаться максимальное снижение уровня энтропии; повторение предыдущих шагов рекурсивно до тех пор, пока в каждой из подвыборок не окажутся объекты одного класса. В случае прогнозирования количественного признака (задачи регрессии) используется другая метрика оценки прироста упорядоченности при разбиении выборки, так называемая дисперсия вокруг среднего: Риc.3.7.Структурарешающегодерева Информационная энтропия представляет собой меру неопределённости некоторой системы (в статистической D 1 |
