Учебником Математика
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
|
III. Изучение нового материала. 1. Формирование восприятия состава числа 5. Работу можно провести по рисунку 1 (с. 34 учебника, часть 1) или с использованием наборного полотна. – Рассмотрите внимательно рисунок. – Что заметили? (На двух лавочках сидят пять девочек.) – Как девочки расположились на лавочках? (Сначала на одной лавочке сидели четыре девочки, а на другой – одна девочка.) Параллельно на наборном полотне или магнитной д о с к е «записывается»: 4 1. Потом на одной лавочке осталось три девочки, а на другой стало – две. З а п и с ь на наборном полотне (магнитной доске): 3 2. Потом на первой лавочке осталось сидеть две девочки, а на второй стало три девочки. З а п и с ь на наборном полотне (магнитной доске): 2 3 . Затем ещё одна девочка пересела на вторую лавочку, и на первой лавочке осталась одна девочка, а на второй их стало четыре. З а п и с ь на наборном полотне (магнитной доске): 1 4. – Посмотрите на записи, сделанные на доске. – Пользуясь записями, расскажите, как можно получить число 5. Учащиеся проговаривают хором: Пять – это четыре и один. Пять – это три и два. Пять – это два и три. Пять – это один и четыре. 2. Упражнение в получении числа 5 разными способами. Далее учитель может провести с детьми игру «Заселяем домик». Можно использовать «домик», помещённый на полях учебника (с. 34, часть 1), но лучше, чтобы «домик» был на доске и дети «заселяли» его магнитными цифрами.  IV. Закрепление знаний учащихся о составе числа 5. Подготовка к восприятию темы «Связь сложения и вычитания». Учитель предлагает ученикам рассмотреть рисунок в задании 2 (с. 34 учебника, часть 1). – Что хотите сказать? (С помощью бусинок показан состав числа 5.) Далее дети записывают на доске или на наборном полотне: 4 + 1 = 5. – Если от 5 бусинок убрать одну, сколько бусинок останется? (Четыре). З а п и с ь: 5 – 1 = 4. В итоге на д о с к е (наборном полотне) появляется следующая запись: 4 + 1 = 5 5 – 1 = 4 3 + 2 = 5 5 – 2 = 3 2 + 3 = 5 5 – 3 = 2 1 + 4 = 5 5 – 4 = 1 – Какой вывод можно сделать? В заключение урока учащиеся выполняют задание 1 (с. 35 учебника, часть 1): сравнивают числа (устно). Задание выполняется фронтально. V. Итог урока. – Что нового узнали? – Чему научились? – Оцените свою работу. У р о к 22. ТОЧКА. КРИВАЯ ЛИНИЯ. ПРЯМАЯ ЛИНИЯ. ОТРЕЗОК Цели урока: дать учащимся первичные представления о кривой линии, прямой линии, отрезке; продолжать работу по усвоению учащимися состава чисел 2–5; продолжать пропедевтику темы «Задача». Ход урока I. Организационный момент. II. Изучение нового материала. 1. Знакомство с новыми понятиями. На доске изображено несколько разных линий. 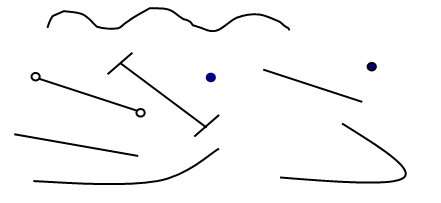 Учитель просит детей внимательно посмотреть на доску и сказать, что они заметили. В результате беседы учащиеся под руководством учителя делят все изображённые на доске объекты на 4 г р у п п ы: точки, кривые линии, прямые линии, отрезки. 2. Графическое изображение изученных линий. Выводы. – Чем прямая линия отличается от кривой? – Каким чертёжным инструментом нужно воспользоваться, чтобы начертить прямую линию? (Линейкой.) – Как вы думаете, почему линейку так назвали? – Про линейку даже есть стихотворение: Я – линейка. Прямота – Моя главная черта. – Начертите в ваших тетрадях одну прямую линию и одну кривую. – Нужна ли линейка, для того чтобы начертить кривую линию? – Поставьте в ваших тетрадях точку. – Как вы думаете, сколько прямых линий можно провести через одну точку? (Высказывания детей.) – Проведите одну прямую линию. – Можно ли провести ещё? – Проведите. – А ещё можно провести прямую линию через эту же точку? – Проведите. – А ещё можно? – Проведите. – Какой в ы в о д можно сделать? (Через одну точку можно провести бесконечно много прямых линий.) – Как вы думаете, можно ли через одну точку провести бесконечно много кривых линий? – Попробуйте это сделать. – Какой вывод из этого следует? – А теперь поставьте в ваших тетрадях две точки. – Сколько через них можно провести прямых линий? (Высказывания детей.) – Проведите прямую линию. – Проведите ещё одну прямую через эти же точки. (Дети пытаются выполнить задание учителя и приходят к выводу, что это сделать невозможно.) – Получилось ли у вас это сделать? – Какой в ы в о д из этого следует? (Через две точки можно провести только одну прямую линию.) – Поставьте ещё две точки в ваших тетрадях. – Сколько кривых можно провести через них? – Проведите одну кривую линию. – Можно ли провести ещё одну кривую линию через эти же две точки? – Попробуйте это сделать. – А ещё одну? – Проведите. – Какой в ы в о д из этого следует? (Через две точки можно провести много кривых линий.) – Проведите прямую линию. – Поставьте на ней две точки. – Часть прямой от одной точки до другой выделите цветным карандашом. – Посмотрите внимательно на доску и найдите линии, похожие на полученную вами. – Как называются эти линии? (Отрезки.) – Чем отрезок отличается от прямой линии? Учитель помогает детям сделать в ы в о д. (Отрезок – это часть прямой линии. Отрезок имеет начало и конец, то есть ограничен с двух сторон точками, в отличие от прямой линии, которая не имеет ни начала, ни конца, то есть бесконечна.) – Начертите в ваших тетрадях два отрезка. В з а и м о п р о в е р к а.  III. Пропедевтика темы «Задача». Учитель предлагает учащимся рассмотреть задание 2 (с. 37 учебника, часть 1). – Как вы думаете, какое задание предстоит выполнить? – Составьте рассказы и поставьте к ним вопросы. – Какое числовое выражение соответствует первому рисунку? – Какое числовое выражение соответствует второму рисунку? – Какие числовые выражения оказались «лишними»? – Составьте по ним рассказы.  IV. Составление и чтение равенств. Учитель может использовать задание 3 (с. 37 учебника, часть 1) и задание 1 (с. 10 в тетради № 1). Р а б о т а п о у ч е б н и к у. – Составьте выражения в соответствии с рисунками. (Выражения могут записываться учащимися в тетрадях с комментированием, а могут быть записаны только на доске.) Учителю следует добиваться от учащихся того, чтобы каждое из записанных выражений они читали разными способами. Р а б о т а в т е т р а д и. Учащиеся читают первое из записанных выражений и закрашивают фигуры, из которых состоит рисунок, в соответствии с выражением. Например:дано выражение 3 + 2 = 5. Учащиеся закрашивают 3 квадрата синим цветом, а 2 квадрата – зелёным. Вся работа выполняется ф р о н т а л ь н о. V. Итог урока. – Какие открытия сделали? – Какая линия называется прямой? – Что такое «отрезок»? – Сколько прямых линий можно провести через 1 точку? – А через две? У р о к 23. ЛОМАНАЯ ЛИНИЯ. ЗВЕНО ЛОМАНОЙ Цели урока: познакомить учащихся с понятиями «ломаная линия», «звено ломаной»; формировать умение чертить по линейке; продолжать пропедевтику темы «Задача»; формировать у детей умение составлять и читать равенства. Ход урока I. Организационный момент. II. Закрепление и повторение изученного о прямой линии, отрезке, кривой линии. Данную работу можно провести по рисункам в заданиях 1 (с. 36, 37 учебника, часть 1) либо по рисункам, подобранным учителем. – Покажите на рисунках прямые линии. – Докажите, что это прямые линии. – Найдите на рисунках отрезки. – Обоснуйте ваше мнение. – Какие линии кривые? – Почему вы так считаете? III. Изучение нового материала. 1. Знакомство с новыми понятиями. На д о с к е изображены различные линии: 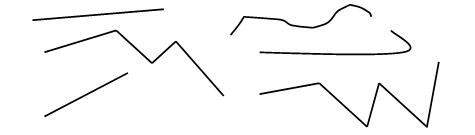 – Что хотите сказать? – На какие группы можно разделить данные линии? – Как бы вы их назвали? Если дети не смогут самостоятельно прийти к названию «ломаная», то учитель сообщает ученикам о том, что такая линия называется ломаной. Учитель может также продемонстрировать учащимся наглядно, как из прямой линии получить ломаную. Далее учитель предлагает ученикам рассмотреть несколько ломаных линий. – Что заметили? – Из каких линий состоят ломаные? (Из отрезков.) – Каждый такой отрезок (часть ломаной) – звено ломаной. Р а б о т а с у ч е б н и к о м. Учитель просит детей сравнить две группы линий на рисунках, данных на полях учебника (с. 38, часть 1). – Что увидели? Затем учитель сообщает детям (в том случае если они сами не смогут найти правильный ответ), что ломаные линии на первом рисунке называются незамкнутыми, а ломаные на втором рисунке – замкнутыми линиями.  1. Формирование умения выполнять чертежи по линейке. Р а б о т а в т е т р а д и. Работа ведётся по заданиям 4 (с. 10 в тетради № 1), 2 (с. 11 в тетради № 1). Учащиеся по линейке соединяют данные в заданиях точки линиями. (Учитель оказывает индивидуальную помощь детям.) – Что получилось? (Ломаные.) – Есть ли среди данных ломаных замкнутые ломаные? – А незамкнутые? Покажите их. – Сколько звеньев в первой ломаной (во второй, в третьей)? IV. Составление и чтение равенств. Работа ведётся по заданию 1 (с. 11 в тетради № 1) и заданию 2 (с. 39 учебника, часть 1). Выполняя задание в тетради, учащиеся, рассмотрев рисунки, составляют равенства, соответствующие рисункам. Например:дано 5 квадратов, 2 из них зачёркнуто; значит, было 5; из 5 вычли 2, осталось 3; получаем равенство 5 – 2 = 3. Аналогичная работа проводится с заданием учебника.  С а м о с т о я т е л ь н а я работа учащихся. Учащиеся самостоятельно решают равенства в задании 3 (с. 39 учебника, часть 1). При выполнении задания ученики могут пользоваться счётным материалом. V. Фронтальная проверка и самопроверка. Один из учащихся читает равенства, называя полученный ответ. Дети могут это делать по очереди; остальные ученики, если у них такой же (правильный) ответ, ставят около него «плюс» карандашом. Если ошибка допущена у того ребёнка, который читает равенство, дети должны обязательно исправить её. VI. Пропедевтика темы «Задача». По рисункам задания 1 (с. 39 учебника, часть 1) учащиеся составляют короткие (математические) рассказы, содержащие вопрос, и подбирают равенства, соответствующие каждому рассказу. Найдя лишнее равенство, дети придумывают по нему рассказ. VII. Итог урока. – Чему учились на уроке? – Что нового узнали? – Что такое «звено ломаной»? – Как вы работали на уроке? У р о к 24. СОСТАВ ЧИСЕЛ 2–5 Цели урока: закреплять у учащихся навыки счёта от 1 до 5 и от 5 до 1, развивать умение получать изученные числа разными способами; закреплять знание учеников об отрезке, прямой линии, ломаной; продолжать работу по составлению и чтению равенств; продолжать подготовительную работу к изучению темы «Задача». Ход урока I. Организационный момент. II. Работа над составом чисел 2–5. 1. Составление и чтение равенств. Учитель предлагает учащимся «сходить» в магазин игрушек. Помогут в этом рисунки из задания 1 (с. 40 учебника, часть 1). Пользуясь рисунками и схемами равенств, учащиеся составляют равенства, которые записываются на доске. (Дети могут «записывать» равенства цифрами и знаками кассы цифр.) В результате на доске появляются следующие з а п и с и: 4 – 1 = 3 4 + 1 = 5 4 – 2 = 2 3 + 2 = 5 4 – 3 = 1 2 + 3 = 5 1 + 4 = 5 Далее учитель просит учащихся рассмотреть рисунки из геометрических фигур и составить по ним равенства. Полученные равенства учащиеся записывают в тетрадях с комментированием. З а п и с ь в тетради: 4 – 2 = 2 4 + 1 = 5  2. Игра «Домино». Учащиеся под руководством учителя сначала разбирают задание 2 (с. 40 учебника, часть 1), проговаривая хором состав записанных чисел: Три – это два и один. Три – это один и два. Пять – это четыре и один. Пять – это один и четыре. Пять – это три и два. Пять – это два и три. Затем учащиеся выполняют задание 2 (с. 40 учебника, часть 1, поля): с а м о с т о я т е л ь н о вставляют пропущенное число, пользуясь кубиком «домино». Данная работа проводится ф р о н т а л ь н о. Так же, как и в предыдущем задании, учащиеся проговаривают хором состав чисел, предварительно вставив нужное число. Далее ученики с а м о с т о я т е л ь н о выполняют задание 3 (с. 9 в тетради № 1): дорисовывают в «домино» необходимое число точек, соответствующее написанной цифре. III. Закрепление навыков счёта. Р а б о т а в т е т р а д и. Учащиеся выполняют задание 4 (с. 13 в тетради № 1). Проанализировав данный номер, дорисовывают такое количество квадратиков, которое соответствует записанной ниже цифре. Затем считают вслух в прямом и обратном порядке от 1 до 5 и от 5 до 1. После этого задания учащиеся прописывают числа от 1 до 5 и от 5 до 1 в порядке увеличения и в порядке уменьшения (с. 11 в тетради № 1, задание 3). В з а и м о п р о в е р к а.  IV. Пропедевтика темы «Задача». По рисункам задания 1 (с. 41 учебника, часть 1) учащиеся составляют короткие (математические) рассказы, содержащие вопрос, подбирают из равенств, записанных ниже, соответствующие рассказам и рисункам, а к оставшимся равенствам придумывают свои рассказы. V. Итог урока. – Чему научились на уроке? – Какими знаниями, приобретёнными сегодня, вам бы хотелось поделиться с друзьями, со старшими? У р о к 25. ЗНАКИ СРАВНЕНИЯ «БОЛЬШЕ», «МЕНЬШЕ, «РАВНО» Цели урока: познакомить учащихся со знаками сравнения «больше», «меньше», «равно»; учить детей писать знаки сравнения «больше», «меньше»; развивать навыки счёта; закреплять знание состава изученных чисел. Ход урока I. Организационный момент. II. Устный счёт. 1. Игра «Назови соседа»: 3 2 4 2. Назовите число, которое: – следует за числом 1; – предшествует числу 5; – на 1 больше числа 3; – на 1 меньше числа 2. Целесообразнее, чтобы на данном этапе урока ученики пользовались карточками с цифрами или индивидуальной дощечкой, на которой они записывали бы ответы. III. Закрепление состава изученных чисел. Для проведения этой работы учитель может использовать задание 1 (с. 43 учебника, часть 1), а также воспользоваться счётным материалом и наборным полотном. Выполняя задание учебника и пользуясь рисунками и данными равенствами, ученики рассказывают, как можно получить число 5. Затем, пользуясь различными фигурками счётного материала и наборным полотном, дети составляют разными способами числа 4, 3.  IV. Изучение нового материала. 1. Знакомство со знаками сравнения. Учитель предлагает детям, используя наборное полотно, сравнить группы различных предметов. Например: 5 зайчиков и 4 лисички; 2 розы и 3 ромашки и т. д. Учащиеся сравнивают (устно) количество предметов. – Можно ли то, что вы сказали, как-то записать? (Высказывания детей.) – В математике существуют специальные знаки. Для того чтобы показать, что одно число больше другого, используют знак «больше» ( > ), а для того чтобы показать, что одно число меньше другого, используют знак «меньше» ( < ). |
