УМКД Надежность. Надежность УМКД 2017 (1). Учебнометодический комплекс дисциплины Надежность технологических машин
 Скачать 1.75 Mb.
|
|
1. Представление о состоянии изделия, как о траектории случайного процесса в фазовом пространстве. Для анализа различных вариантов потери машиной или отдельной системой работоспособности целесообразно вначале представить данный процесс в общем виде, как некоторую абстрагированную математическую модель. Каждое изделие характеризуется некоторыми выходными параметрами (параметрами функционирования) Х1; Х2; …; Хn , которые определяют его состояние и являются случайными функциями времени Х(t). Поэтому работоспособность системы, как общая характеристика ее состояния, также изменяется во времени. Если воспользоваться понятиями теории множеств, то можно рассматривать область работоспособности изделия, как такое множество G состояний, определяемых значениями параметров Хі , при котором отказа не происходит. Принадлежность данного состояния Х(t) множеству G , т.е. Х(t) € G будет означать, что изделие работоспособно. Если любое значение Хі вышло за границу данного множество, то произошел отказ изделия, оно стало неработоспособным. Если состояние изделия характеризуется несколькими выходными параметрами и будет происходить процесс изменения всех n параметров, то множество G будет связано с n–мерным, так называемым фазовым пространством. Процесс потери машиной работоспособности может быть представлен в виде траектории случайной функции Х(t) в n–мерном фазовом пространстве. Фазовая траектория может быть описана вектор - функцией Х(t) с составляющими по осям координат Х1(t); Х2(t); …; Хn(t) и начальными координатами системы (в момент времени t= 0) Х01 ; Х02 ; ...; Х0n . Границы множества G определяются предельно допустимыми значениями параметров Х1 max; Х2 max; ….Хnmax . 2. Анализ области работоспособности изделия. Рассмотрим область работоспособности изделия в представлениях n–мерного фазового пространства. Границы области G зависят от требований к изделию. Более высокие требования к его выходным параметром сужают область работоспособности. Для одного и того же изделия в зависимости от характера выполняемой работы могут предъявляться различные требования и точности его функционирования. Говоря об области работоспособности изделий, следует различать действительную G, которая определяет требуемую работоспособность изделия, и расчетную G ′, которая диктуется требованиями ТУ к отдельным параметрам. Кроме того, часто о предельном состоянии изделия судят по косвенным показателям, функционально связанным с его работоспособностью. 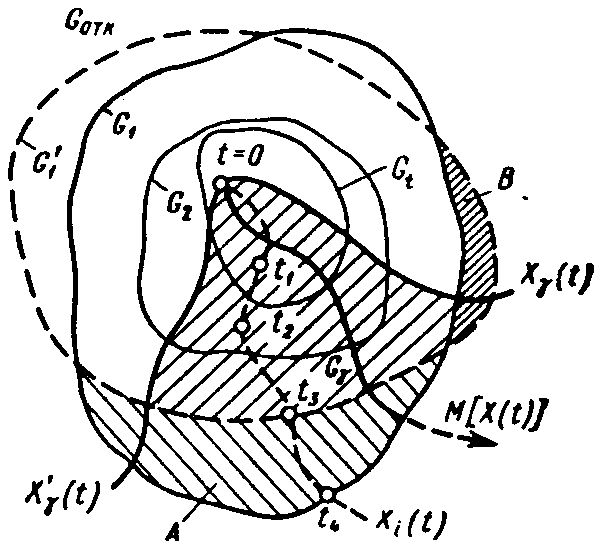 Рисунок 4. Области работоспособности и состоянии изделия. Из рис.4 видно, что между областями действительной G1 и расчетной G′1 работоспособностей изделия имеется разница. В зависимости от соотношения их границ может существовать область неиспользованных возможностей А, когда ТУ изделие считается потерявшим работоспособность, хотя оно еще может правильно функционировать, и область неучтенных параметров В, когда согласно ТУ можно эксплуатировать изделие, которое в действительности уже стало неработоспособным. Кроме того, в ряде случаев целесообразно ввести понятие об устойчивости изделия к отказам, что особенно важно при высоких требованиях к надежности. Совокупность реализаций фазовой траектории случайного процесса Х(t) и анализ возможного характера протекания процесса во времени определит область состояний Gt, т.е. такую область в фазовом пространстве, в которую попадают все значения параметров за данный промежуток времени t = Т. Если эта область является частью области работоспособности G, т.е. его подмножеством Gt  G, то изделие будет устойчиво по отношению к отказам, так как вероятность его возникновения F(t)=0. это условие можно записать так же, как X(t=T) Gt, т.е. любые значения параметров Х1; Х2; …; Хn , определяющие случайный вектор в пределах периода времени t = T будут принадлежать множеству, которое является подмножеством области работоспособности. Вероятность возникновения отказа наступит лишь после того момента времени когда, условие нарушится и будет возможно пересечение множеств Gt и G. До этого периода времени работа изделия будет протекать в устойчивой зоне по отношению к отказам и запас устойчивости может характеризоваться значением Кн – запасом надежности.3. О формализации процесса потери работоспособности. Построение математической модели потери машиной работоспособности является весьма сложной и во многих случаях трудно решимой задачей. Наличие случайных факторов не позволяет строить полностью детерминированные модели, когда определенная совокупность исходных параметров и действующих факторов однозначно определяет изменение выходных параметров во времени. Математическая модель должна быть результатом формализации описания процесса потери машиной работоспособности и учитывать все основные закономерности процесса. При этом учет большого числа действующих факторов ведет к усложнению модели, что не всегда оказывается оправданным. Формализация и построение математической модели складывается обычно из следующих последовательных этапов: Описание процесса Формализованная схема процесса Математическая модель  Рисунок 5. Описание процесса концентрирует сведения о физической природе протекающих процессов старения, условиях эксплуатации изделия, количественных характеристиках элементарных явлений, результатах наблюдений за работоспособностью изделия при эксплуатации и испытаниях. Формализованная схема процесса – это промежуточный этап к построению математической модели. Она полностью использует данные экспериментального исследования процесса. В схеме процесса, как правило, графически или в виде таблиц представляются основные зависимости а выясняются все вопросы, связанные с интерполяцией и экстраполяцией экспериментального материала. Математическая модель представляет собой систему соотношений, связывающих характеристики процесса и исходные показатели изделия с его выходными параметрами. Из-за сложности явлений часто процесс работоспособности расчленяют на несколько элементарных процессов, которые можно описать более простыми математическими зависимостями. 4. Взаимодействие машины со средой, как система автоматического регулирования. Рассматривая процесс потери машиной работоспособности, который выражается в изменении ее выходных параметров во времени, при формализации этого процесса всегда следует учитывать причины, вызывающие эти явления. Эти причины, как было показано выше связаны с воздействием на машину различных видов энергии, приводящих к возникновению процессов, снижающих начальные параметры изделия. На характер реализаций случайных функции, описывающих траекторию изменения состояния в фазовом пространстве, решающее влияние оказывает физика процессов старения и их взаимодействие с изделием. При рассмотрении влияния, которое оказывают различные процессы на выходные параметры машины, следует учитывать, что на скорость процесса может влиять и обратная связь, которая существует между состоянием машины и теми процессами, которые в ней протекают. Например, износ отдельных механизмов машины может не только уменьшить точность ее функционирования, но и привести к повышению динамических нагрузок, которые, в свою очередь, интенсифицируют процесс изнашивания элементов машины. Температурные деформации отдельных звеньев могут не только исказить положение узлов машины и этим повлиять на точность работы, но и привести к повышенным нагрузкам и, как следствие, к повышенному тепловыделению в механизмах. Известно также, что при возникновении колебаний в машине имеется обратная связь между ее упругой системой и данным рабочим процессом или трением, которые являются источниками колебаний. На основании сказанного можно представить взаимодействие машины с протекающими в ней процессами в виде замкнутой системы автоматического регулирования (рис. 6). Для анализа изменения состояния сложных систем может быть применен аппарат теории автоматического регулирования. Здесь вместо управляющих воздействий и внешних возмущений будет иметь место силовые, температурные, химические и иные воздействия на машину. Реакцию различных звеньев на внешние возмущения в данном случае можно оценивать переходными характеристиками или передаточными функциями. 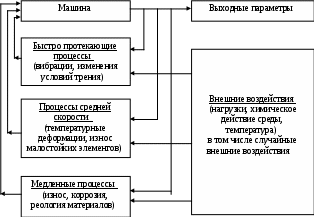 Рисвунок 6. Взаимодействие машины со средой как система автоматического регулирования В табл.3 показаны типовые переходные характеристики, применительно к процессам потери машиной и ее элементами работоспособности. Таблица 3. Переходные процессы при изменении работоспособности изделия
Следует иметь в виду, что изменение выходных параметров сложного изделия – это результат многочисленных изменений в отдельных звеньях системы в разные периоды времени. Поэтому при изучении надежности машины всегда должно сочетаться исследование функциональных связей и физических закономерностей с оценкой стохастических процессов, характеризующих изменение начального состояния изделия. /Л.1, Л.4/. Контрольные вопросы: Анализ и расчет надежности. Законы распределения. Экспоненциальный закон. Закон Вейбулла. Нормальный закон. Закон гамма. Модуль III Прогнозирование надежности машин Лекция 6. Тема: Надежность сложных систем 1. Сложная система и ее характеристики. 2. Элементы сложной системы. 3. Основные типы структур сложных систем. 4. О надежности сложных систем. 5. Эффективность системы. Сложная система и ее характеристики. Под сложной системой будем понимать объект, предназначенный для выполнения заданных функции, который может быть расчленен на элементы, каждый из которых также выполняет определенные функции и находится во взаимодействии с другими элементами системы. Понятие сложной системы условна. Оно может применяться к отдельным узлам и механизмам к машинам и к системам машин. С позиций надежности сложная система обладает как отрицательными, так и положительными свойствами. Факторы, отрицательно влияющие на надежность сложных систем, следующие. Во-первых, это большое число элементов, отказ каждого из которых может привести к отказу всей системы. Во-вторых, сложные системы часто являются уникальными или имеются в небольших количествах. В этом случае статистические данные не могут быть использованы для оценки их работоспособности. Это усугубляется также тем, что даже одинаковые системы работают в различных условиях эксплуатации и выполняют неодинаковые функции, поскольку их возможности весьма широки. В-третьих, даже у систем и машин одинакового конструктивного оформления каждый экземпляр имеет индивидуальные черты. Незначительные вариации свойств отдельных элементов сказываются на выходных параметрах системы. Подобно биологическим системам и для технических устройств можно высказать следующее положение: чем сложнее система, тем большими индивидуальными особенностями она обладает. Это положение весьма важно и для разработки методов испытания сложных систем. Однако сложные системы обладают и такими свойствами, которые положительно влияют на их надежность. Во-первых, сложным системам свойственна в той или иной мере самоорганизация, саморегулирование или самоприспособление, когда система способна найти наиболее устойчивое для своего функционирования состояние. Во-вторых, для сложной системы часто возможно восстановление работоспособности по частям, без прекращения ее функционирования. В-третьих, не все элементы одинаково влияют на надежность сложной системы. Многие из них сказываются лишь на эффективности ее работы. Анализ работоспособности сложной системы связан с изучением ее структуры и тех взаимосвязей, которые определяют ее надежное функционирование. Важную роль при этом играет выделение элементов, составляющих данную систему. 2. Элементы сложной системы. При анализе надежности сложных систем их разбивают на элементы (звенья) с тем, чтобы вначале рассмотреть параметры и характеристики элементов, а затем оценить работоспособность всей системы. Под элементом будем понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными параметрами. Элемент обладает следующими особенностями: он выделяется в зависимости от поставленной задачи, может быть достаточно сложным и состоять из отдельных деталей и узлов; при исследовании надежности системы элемент не расчленяется на составные части и показатели безотказности и долговечности относятся к элементу в целом; возможно, восстановление работоспособности элемента независимо от других частей и элементов системы. При анализе сложных систем их часто разбивают на подсистемы для последовательного рассмотрения надежности всех составных частей системы. Выходные параметры каждого элемента при их изменении в процессе эксплуатации должны учитывать требования, предъявляемые к надежности всей системы. Если рассмотреть выходные параметры каждого элемента (их может быть один или несколько), то они могут по-разному влиять на формирование выходного параметра всей системы ХΣ, определяющего ее надежность. Можно выделить три основных свойства этих параметров (рис. 7). 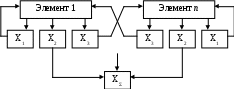 i 1 п Рисунок 7. Выходные параметры элементов сложной системы Х1 – изменение параметра влияет на работоспособность лишь самого элемента. Отказ данного элемента ведет, как правило, к отказу изделия. Х2 – параметр участвует в формировании одного (или нескольких) выходных параметров всего изделия. Его изменения должны учитываться в совокупности с изменением параметров данной категории для других элементов. По отклонению от номинала только данного параметра нельзя судить об отказе элемента. Х3 – параметр влияет на работоспособность других элементов. Его изменение для остальных частей изделия аналогично изменению внешних условий работы. Следует отметить, что каждый параметр может обладать одним или несколькими из перечисленных свойств. В зависимости от того, какие свойства выходных параметров элементов преобладают, будут формироваться и основные черты сложных изделий. |
