УМКД Надежность. Надежность УМКД 2017 (1). Учебнометодический комплекс дисциплины Надежность технологических машин

• Название: Учебнометодический комплекс дисциплины Надежность технологических машин
• Анкор: УМКД Надежность
• Дата: 23.01.2022
• Размер: 1.75 Mb.
• Имя файла: Надежность УМКД 2017 (1).doc
• Тип: Учебно-методический комплекс; #339787
• страница: 14 из 16

Тема: Законы распределения наработки до отказа

Цель занятия:

Основные вопросы к практическому занятию:

1. 
   Основные виды отказов
   
2. 
   Основные недопустимые отказы
   
3. 
   Вероятность безотказной работы.
   

Задание:

При анализе и расчетах надежности одной из необходимых операций является установление на основании статистических данных закона распределения вероятностей наработки объекта до отказа или других случайных величин — времени восстановления, числа отказов за некоторый период эксплуатации, срока службы и других. При расчетах надежности деталей машин в основном используются следующие законы распределения: экспоненциальный, Вейбулла, нормальный и гамма.

При установлении закона распределения учитывают в основном два фактора: форму теоретической кривой плотности распределения и природу отказов. На рис. I.2 приведен характерный вид кривых плотности распределения наработки между отказами во времени и других характеристик надежности для различных законов. Рассмотрим эти законы и их свойства.

Экспоненциальный закон характеризуется плотностью распределения наработки (времени)-до отказа (плотностью вероятности отказов)

;

где λ – интенсивность отказов (параметр закона распределения). функция распределения

. Вероятность отказа за время t

,

Вероятность безотказной работы (функция надежности)


Средняя наработка (среднее время работы) до возникновения отказа равна математическому ожиданию наблюдаемых значений наработки до отказа (времени безотказной работы) объекта



Дисперсия наработки до отказа (времени безотказной работы)



Среднеквадратичное уклонение наработки да отказа (времени безотказной работы)



Равенство среднеквадратичного отклонения среднему времени безотказной работы - характерный признак экспоненциального закона. Этот признак на практике используют для проверки истинности гипотезы о существовании экспоненциального закона. Для этого из статистических данных определяют среднее время работы и среднеквадратичное отклонение. Если они близки по значению, то это может служить подтверждением правдоподобия принятой гипотезы. При экспоненциальном законе интенсивность отказов является величиной постоянной, обратно пропорциональной среднему времени безотказной работы.

Это означает, что если время работы объекта до отказа подчиняется экспоненциальному закону, то предшествующее использование объекта до некоторого момента времени t не влияет на остаточное время его работы до отказа, т.е. распределение остаточного времени безотказной работы будет таким же, как если бы в этот момент времени (в момент t) начал использоваться совершенно новый объект. Это свойство экспоненциального закона с практической точки зрения означает, что в процессе эксплуатации объект не испытывает влияния износа, т.е. не стареет. Следовательно, для отказов износового характера этот закон неприменим. Он характерен для внезапных, аварийных отказов, связанных с поломками и разрушениями объекта. Хотя указанное свойство экспоненциального закона противоречит естественному представлению о том, что при эксплуатации объекты подвергаются износу, влияющему на длительность их последующей безотказной работы, этот закон широко применяется в теории надежности. Благодаря простоте аналитического выражения, расчеты надежности для этого закона существенно упрощаются. Применение экспоненциального закона дает возможность получить результаты, пригодные для оценки надежности вновь разрабатываемых объектов.

Экспоненциальный закон с достаточной для практики степенью точности может использоваться и по отношению но времени восстановления:

;

где g(t) – плотность распределения времени восстановления;

μ – интенсивность (параметр потока) восстановлений;

Т_В – среднее время восстановления.

Экспоненциальный закон играет весьма важную роль в теории надежности еще и потому, что он характеризует собой простейший поток событий (отказов и восстановлений), что позволяет применить теорию марковских процессов при расчете показателей надежности сложных систем.

Закон Вейбулла в отличие от экспоненциального имеет два параметра и задается плотностью распределения вероятностей наработки (времени) до отказа в виде



и функцией распределения



где а — параметр масштаба (задает масштаба кривой распределения по оси абсцисс);

в — параметр формы (определяет остроту и асимметрию кривой плотности распределения).

Функция надежности



вероятность отказа



интенсивность отказов



Величины а и б всегда положительны. При в = I распределение Вейбулла переходит в экспоненциальное, которое таким образом является частным случаем распределения Вейбулла. При в < I интенсивность отказов λ(t) становится убывающей функцией времени, поэтому закон Вейбулла с параметром в < I можно использовать для оценки надежности объектов в период их приработки и в других случаях, когда преобладают внезапные отказы. При в > I распределение Вейбулла характеризуется возрастающей интенсивностью отказов и его удобно использовать для оценки надежности "стареющих" объектов, т.е. в которых преобладают из носовые отказы, в частности при ускоренных испытаниях.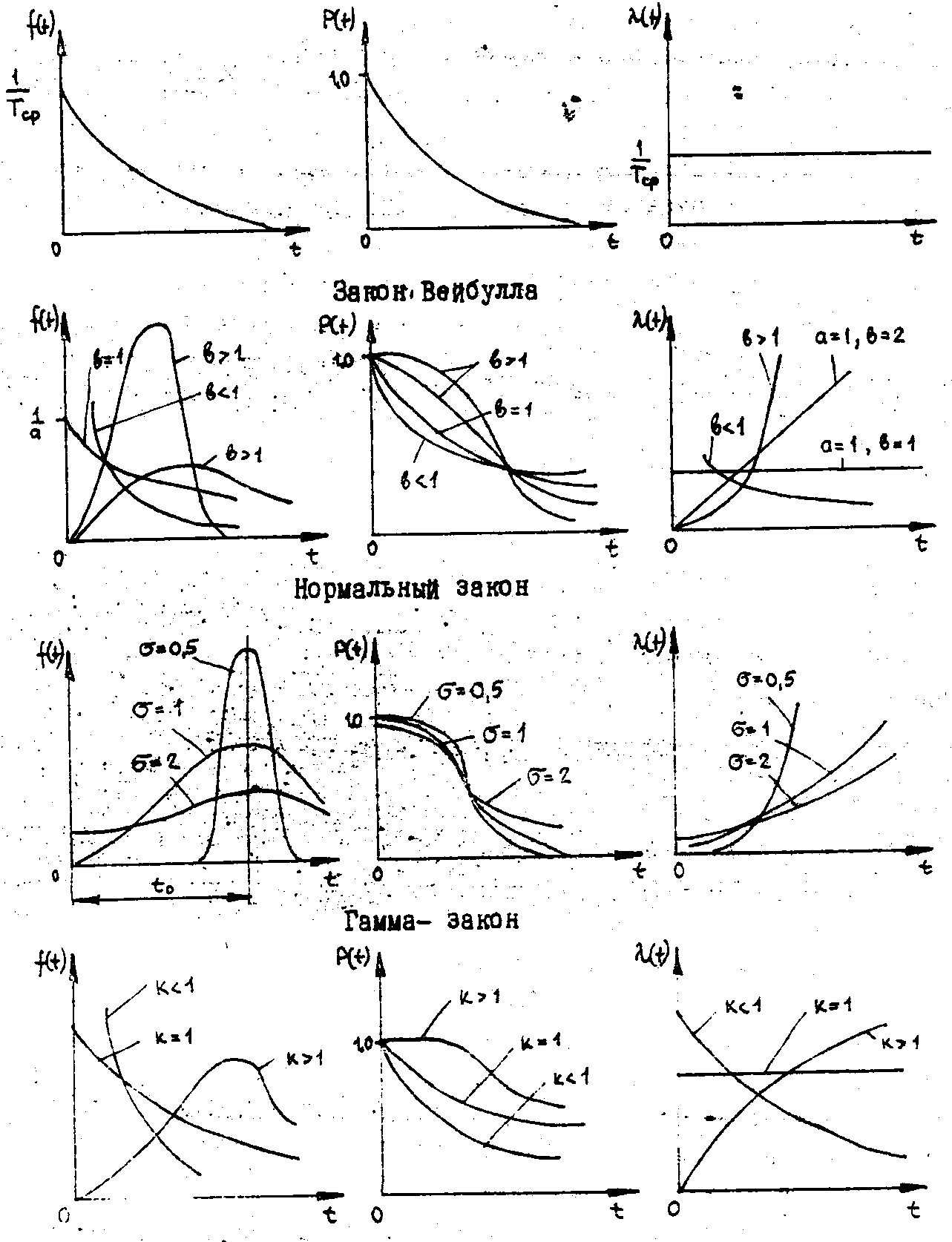

Рисунок 20. Кривые изменения количественный характеристик надежности f (t), Р(t), λ(t) во времени для различных законов распределения.
В этом случае кривая плотности распределения приобретает колоколообразную форму, приближающуюся к форме кривой нормального закона распределения при значениях в = 3,5 ÷ 4,0.

Распределение Вейбулла получило широкое распространение при расчетах надежности , во многом благодаря наличию второго параметра в . Подбирая наиболее подходящие параметры а и в, можно добиться более полного соответствия теоретического закона распределения опытным данным, чем экспоненциального, зависящего от одного. параметра Х, Распределение. Вейбулла применимо для описания случаев нестационарного потока отказов с изменяющейся плотностью потока во времени. Оно хорошо описывает отказы усталостные, возникающие в результате совместного воздействия износа и ударных нагрузок, например отказы шарикоподшипников, объектов, состоящих из последовательно соединенных дублированных элементов и другие.

Нормальный закон хорошо описывает распределение вероятностей наработки до отказа (времени безотказной работы) объектов, когда она зависит от большого числа однородных по своему влиянию случайных факторов, влияние каждого из которых по сравнению с совокупностью всех остальных незначительно. Этот закон характерен для постепенных отказов, вызванных износом и старением.

Плотность нормального распределения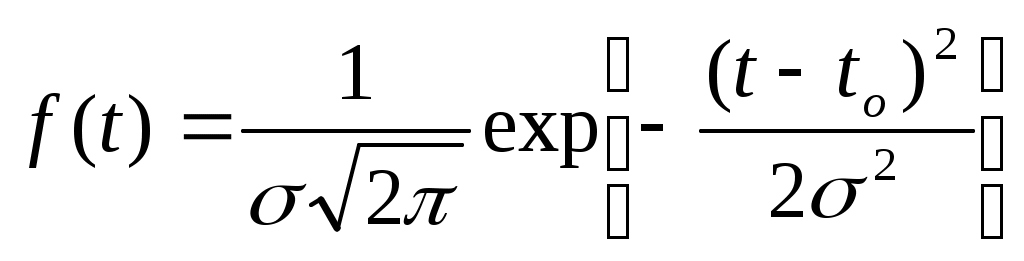



Функция распределения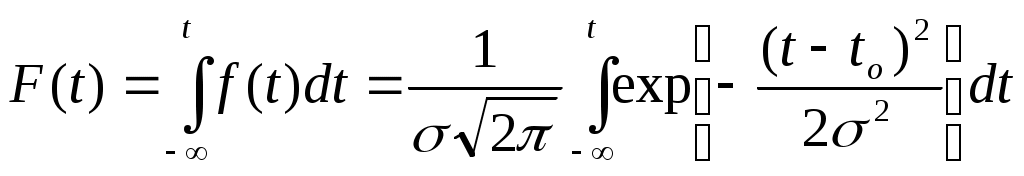



где t_о — математическое ожидание наработки до отказа (времени безотказной работы);

σ — среднеквадратичное отклонение наработки до отказа (времени безотказной работы).

Параметр t_о характеризует положение центра группирования распределения на оси абсцисс, параметр σ - форму кривой плотности распределения. При увеличении σ максимальная ордината кривой, соответствующая t_о, уменьшается, а сама кривая становится более плоской, растягиваясь вдоль оси абсцисс (рис.20).

Характерным признаком нормального распределения является монотонное возрастание интенсивности отказов λ (t) с момента начала эксплуатации объекта.

Вероятность отказа объекта в интервале (0, t )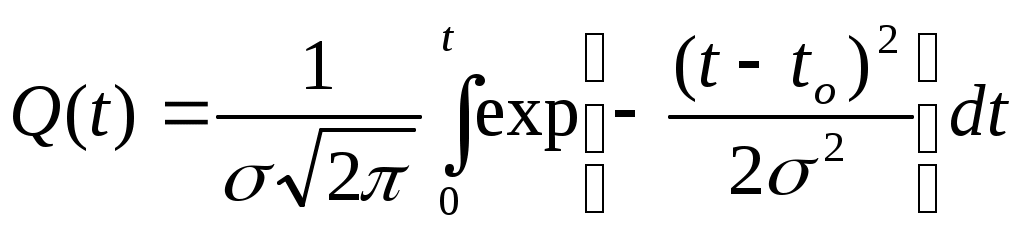



вероятность безотказной работы (функция надежности)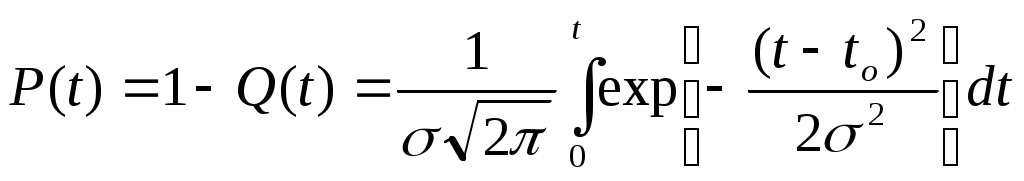



Чтобы упростить расчеты, переходят к нормированному нормальному распределению, у которого центр группирования совмещен с началом координат, а значения абсциссы выражены в долях σ.

Нормирование заключается в переходе от величины t к вспомогательной линейной функции .

Плотность нормированного распределения



функция нормированного распределения



Эта функция называется нормированной функцией Лапласа. При отрицательных значениях z Ф(-z) = -Ф(z).

Для вычисления функции Лапласа составлена таблица. Нормальная функция распределения F(t) .выражается через функцию Лапласа как



Особенность нормального закона заключается в том, что практически все рассеяние (99,73 %) случайной величины укладывается на участке t_о±3σ, т.е. вокруг центра группирования в пределах шести среднеквадратичных отклонений. Это позволяет зная. Значения t_о и σ, практически определить диапазон возможных значений случайной величины.

Поскольку длительность безотказной работы объекта не может быть отрицательной, нормальное распределение в его общем виде к задачам надежности может применяться только при σ ≤ t_о, т.е. когда

Если условие σ ≤ t_о, не выполняется, то применяется "усеченный нормальный закон".

Сущность усечения заключается в том, что из нормальной совокупности значений случайной величины исключаются все значения t<0. Для усеченного распределения при t<0.

При значениях t≥0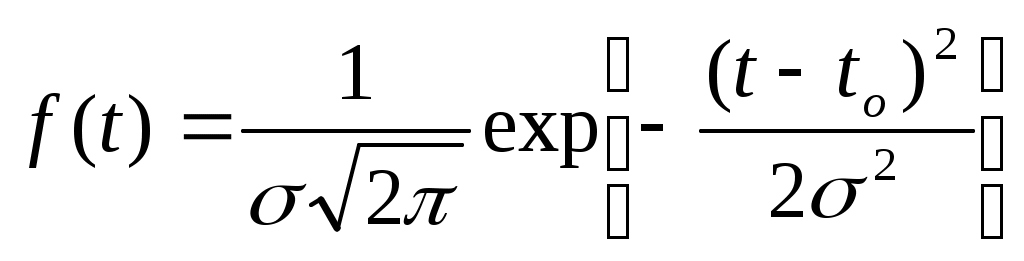



где А – нормирующий постоянной множитель.

Значение А вычисляют по формуле



где – функция Лапласа;

σ и t_о – математическое ожидание и cpеднеквадратичное отклонение отработки до отказа (времени безотказной работы) соответствующего неусеченного распределения усеченное нормальное распределение наблюдается при постепенных отказах объектов и широко используется при анализе надежности сложных систем с учетом ухода параметров элементов (прочности, вибраций, температуры и др.) за допустимые пределы.

Однако при , что имеет место в большинстве случаев при расчетах надежности с нормальным распределением времени безотказной работы, множитель А мало отличается от единицы и усеченное нормальное распределение достаточно точно списывается обычным нормальным распределением.

Закону гамма-распределения подчиняется распределение наработки до отказа (времени безотказной работы) резервированных объектов, элементы которых (основной и резервные) имеют экспоненциальное распределение: наработки до отказа. Этому закону также подчиняется распределение наработки восстанавливаемых нерезервированных объектов при определенной числе отказов.

Плотность распределения наработки в. случае гамма-распределения имеет вид



Если k — целое число, то функция распределения

,

где k — параметр формы; λ_о — масштабный параметр.

Параметр k представляет собой число элементов (основного и резервных) резервированного объекта или число отказов во время испытаний нерезервированных объектов с экспоненциальный распределением. Параметр λ_о представляет собой интенсивность отказов во время испытаний.

Вероятность безотказной работы резервированного объекта

,

где i — обозначение i-го элемента; (k-I) — число резервных, элементов.
Средняя наработка до k-го отказа нерезервированного объекта при одном испытании равна математическому ожиданию наблюдаемых значений наработки до отказа T_o = М (t) = k / λ_о.

Дисперсия наработки до отказа

.

Интенсивность отказов резервированного объекта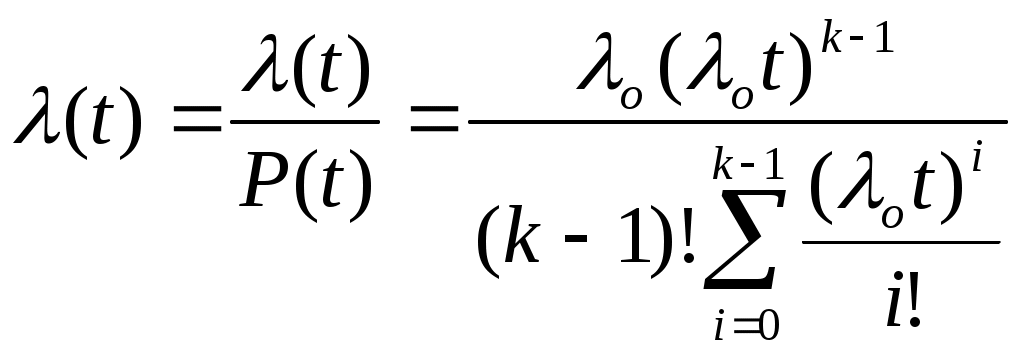



В зависимости от величины параметра k существенно изменяется вид основных количественных характеристик надежности. При k = I закон гамма-распределения превращается в экспоненциальный, при k > I интенсивность отказов возрастает, при k < I - убывает.

Гамма-распределение может хорошо описывать наработку до отказа (время до возникновения отказов) сложных систем, если имеют место мгновенные отказы элементов в начальной стадии эксплуатации или в процессе приработки систем.

При увеличении k гамма-распределение приближается к колоколообразному симметричному распределению, а интенсивность отказов будет иметь все более выраженный характер функции, возрастающей по времени.

Гамма-распределение также используется для описания времени до п-го отказа системы, если исходное распределение наработки до отказа является экспоненциальным.

Кроме рассмотренных, в теории надежности применяются и другие законы распределения — Релея, логарифмически нормальный, распределение g и др. Однако они встречаются более редко.

Различные законы распределения с одной стороны характеризуют различную природу отказов, а с другой — могут быть применены для описания отказов одинакового вида. Это затрудняет правильный выбор закона в каждом конкретном случае, особенно без большого объема результатов испытаний.

И все же наиболее универсальным является закон Вейбулла по следующим причинам:

I) экспоненциальный закон и закон Релея являются частными случаями закона Вейбулла при коэффициентах формы, равных соответственно единице и двум;

2) усеченное нормальное распределение достаточно хорошо описывается распределением Вейбулла при коэффициенте формы 3,5;

3) логарифмически нормальное распределение настолько хорошо аппроксимируется распределением Вейбулла, что для получения заметного статистического различия между ними необходимо не менее тысячи наблюдений.
Лабораторные занятие №5

Тема: Расчет надежности элементов

Цель занятия: Надежность невосстанавливаемых элементов характеризуется показателями безотказности — вероятностью безотказной работы, средней наработкой до отказе и интенсивностью отказов, а также показателем долговечности — гамма-процентным ресурсом.

Основные вопросы к практическому занятию:

1. 
   Работоспособность и надежность машин.
   
2. 
   Как характеризуется изделия выходными параметрами.
   
3. 
   Классификация машин по надежности.
   

Задание:

Элементы разделяют на невосстанавливаемые, у которых рассматривают только первичные отказы, и восстанавливаемые – у которых рассматривают первичные и повторные отказы. Если у восстанавливаемых элементов рассматривают только первичные отказы, то для них справедливы все рассуждения и формулы, относящиеся к невосстанавллваемым объектам.

На основании статистических данных об отказах эти показатели вычисляют по формулам, приведенным выше.

Пример 2.1. Наблюдали за отказами N_о=2подшипников качения. Наработка их t_i до отказа составила, ч: 21, 42, 68, 36, 18, 49, IF, 22, 74 и 19. Вычислить вероятность безотказной работы в течение 40 ч, интенсивность отказов в период между 20 и 50 ч работы и среднюю наработку до отказа подшипников.

Решение: Так как до момента времени t = 40 ч безотказно проработали подшипники с наработкой 42, 68, 49 и 74 ч, (4 подшипника), то вероятность безотказной работы



Интенсивность отказов в период между 20 и 50 ч работы
I/ч

Средняя наработка до отказа
ч,
Пример 2.2.

Время безотказной работы сальникового уплотнения гидроцилиндра подчиняется закону Вейбулла с параметрами в=1,5; а=1000. Вычислить вероятность безотказной работы и интенсивность отказов уплотнения в течение 100 ч после начала эксплуатации.

Решение. Вероятность безотказной работы вычисляем по формуле


Интенсивность отказов
I/ч

Пример 2.3.

При испытании на износ N_о = 100 одинаковых зубчатых колес в течение t = 300 ч из строя вышли 8 колес. Определить вероятность безотказной работы колес за 300 ч и 90 %-ный ресурс работы колес при условии, что время их безотказной работы подчиняется экспоненциальному закону с параметром λ = 0,03 I/ч.

Решение. Вероятность безотказной работы колес в течение 300 ч ; 90 %-ный ресурс работы колес определяют из выражения 900/100; отсюда ч. Это значит, что время работы 100 зубчатых колес, в течение которого вероятность их безотказной работы будет на менее 0,9, составит не менее 3,51 ч.

Функционирование восстанавливаемого элемента с точки зрения теории надежности представляет собой последовательность чередующихся интервалов работоспособного состояния и восстановления работоспособности после отказа. Так же, как у невосстанавливаемых, надежность восстанавливаемых элементов характеризуется вероятностью безотказной работы. Кроме этого показателя, применяется ряд других. Если не учитывают время восстановления элемента, то моменты отказов формируют поток отказов, и количественными показателями надежности элемента в этом случае являются параметр потока отказов и наработка на отказ. На основании статистических денных об отказах эти показатели вычисляют по ранее приведенным формулам.

Характеристикой потока отказов восстанавливаемых элементов является среднее время между отказами — наработка на отказ в течение времени от наработки t₁ до наработки t₂

,

где и – ведущие функции элемента за время t₂ и t₁, соответственно.

При учете времени на восстановление работоспособности элемента пользуются комплексными показателями надежности — коэффициентам готовности К_Г, оперативной готовности К_О.Г. технического использования К_Т.И.

Пример 2.4.

В результате наблюдения за работой редуктора было зарегистрировано r=8 отказов. Наработки t_i между отказами составили, сут: 18, 9, 14, 27, 16, 8, 14, 22. Определить наработку на отказ редуктора и вероятность его безотказной работы в пределах наработки, равной 20 ч.

Решение. Наработка на отказ редуктора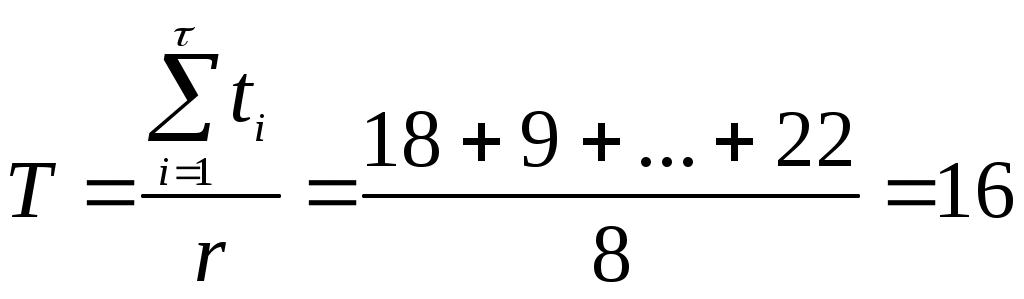

сут

Вероятность безотказной работы ,

где N_σо — число наработок, в течение которых редуктор работал безотказно 20 ч и более. В данном примере N _σо = 2 (22 и 27 ч). Тогда

.
Лабораторные занятие №6