УМКД Надежность. Надежность УМКД 2017 (1). Учебнометодический комплекс дисциплины Надежность технологических машин

• Название: Учебнометодический комплекс дисциплины Надежность технологических машин
• Анкор: УМКД Надежность
• Дата: 23.01.2022
• Размер: 1.75 Mb.
• Имя файла: Надежность УМКД 2017 (1).doc
• Тип: Учебно-методический комплекс; #339787
• страница: 13 из 16

Тема: Элементы теории вероятностей, используемые при расчетах надежности

Цель занятия: Последовательность состояний объекта при переходах называется цепью. Каждый переход называется шагом процесса, который совершается через некоторые промежутки времени, принимаемыми обычно равными некоторой единице времени.

Основные вопросы к практическому занятию:

1. 
   Вероятность безотказной работы.
   

Задание:

Возникновение отказов деталей машин связано с совместным воздействием большого числа различных факторов — динамических нагрузок, высоких температур, влажности и запыленности окружающей среды, несоблюдением правил технической эксплуатации, недостаточным качеством технического обслуживания и ремонта и др. Поэтому отказы носят случайный характер, а сам отказ трактуют как случайное событие.

Главной характеристикой случайного события А является вероятность р(А) его появления в результате испытания. Испытанием называется осуществление какого-либо комплекса условий, который может быть воспроизведен сколь угодно большое число раз. При расчетах надежности испытаниями обычно считают многократно повторяющиеся периоды эксплуатации, в течение которых накапливают статистические данные об отказах.

Вероятность события А — это. отношение числа возможных результатов испытания, благоприятствующих появлению события А, к общему числу всех возможных результатов испытания:

р(А) = т/n,

где т — число результатов испытания, благоприятствующих событию А;

n — общее число всех возможных результатов испытания.
Случайное событие называется достоверным, если в результате испытания оно обязательно происходит. Случайное событие, которое в результате испытания заведомо не может произойти, называется невозможным.

В каждом испытании могут происходить несколько различных случайных событий, которые могут быть несовместимыми или совместимыми, независимыми или зависимыми.

Несовместимыми называются два таких случайных события, которые не могут произойти в одном и том же испытании.

Особенно существенными являются группы попарно несовместимых событий. Например, когда имеет место группа из трех событий, заключающихся в появлении отказа, переходе оборудования в работоспособное состояние или в состояние технического обслуживания, два из этих событий не могут появиться одновременно.

Независимыми называются такие случайные события, когда появление одного из них не влияет на возможность появления остальных.

При решении задач надежности используют понятие частоты события ω (А), которая представляет собой отношение числа результатов испытания, в которых событие А появилось, к общему числу п результатов испытания ω (А) = т / п .

В теории вероятностей доказывается, что при неограниченном увеличении числе опытов в испытании (числа результатов испытания) частота приближается к вероятности события и является ее приближенной оценкой. Частоту называют статистической вероятностью (рассчитанной по данным испытания), поэтому свойства вероятности применимы и к частоте.

Для решения задач надежности используют следующие теоремы теории вероятностей [2]

1. Теорема сложения вероятностей несовместимых событий: вероятность суммы несовместимых событий равна сумме их вероятностей и равна вероятности того, что произойдет хотя бы одно из них р(А₁ + А₂ + … +А_т) + р(А₁) + р(А₂)+ … + р(А_т).

Случайные события А , А2,..., А_т образуют полную группу событий, если они попарно несовместимы; сумма вероятностей несовместимых событий, образующих полную группу, равна единице

р(А₁) + р(А₂)+ … + р(А_т) = 1.

Два несовместимые случайных события, образующих полную группу, называются противоположными. Событие, противоположное А, обычно обозначают А. Для противоположных событий справедливо равенство .

Этим соотношением широко пользуются на практике, когда вычислить вероятность противоположного события проще, чем основного. В частности, при расчетах надежности иногда бывает проще вычислить вероятность отказа, чем безотказной работы, которые являются противоположными событиями.

2. Теорема умножения вероятностей независимых событий: вероятность совместного появления таких событий равна произведению их вероятностей р(АВ)=р(А)·р(В).

3. Теорема умножения вероятностей зависимых событий, т.е. таких, когда вероятность появления одного из них зависит от появления или непоявления другого. Для вычисления вероятности появления зависимых событий пользуются условной вероятностью, обозначаемой р(А/В). Это вероятность появления события А при условии, что событие В, имеющее положительную вероятность, уже произошло.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое уже наступило, т.е. р(АВ)=р(В)·р(А/В).

Случайной называется величина, которая в результате испытания может принимать одно из возможных заранее неизвестных значений.

В теории надежности оперируют с такими случайными величинами, как наработка до отказа, число отказов или число отказавших объектов за некоторый период эксплуатации, время восстановления объекта и др. Случайные величины аналогично случайным событиям могут быть зависимыми и независимыми.

Случайная величина называется дискретной, если она может принимать конечное или бесконечное множество значений, т.е. если эти значения могут быть пронумерованы в каком-нибудь порядке. К дискретным случайным величинам относятся данные статистических (эмпирических) наблюдений об отказах объектов — наработка до отказа, число отказов, число отказавших объектов и др.

Случайная величина называется непрерывной, если она может в результате испытания принять любое значение в одном или нескольких заданных интервалах. Эти значения образуют несчетное бесконечное множество (континуум).

Для полной характеристики случайной величины необходимо задать не только все возможные ее значения, но и закон распределения.

Законом распределения называется зависимость, устанавливающая связь между возможными значениями случайной величины и их вероятностями. При расчетах надежности установление закона распределения является необходимой процедурой для получения исходных данных для расчета показателей надежности.

Закон распределения дискретной случайной величины можно задать таблично, графически или аналитически (в виде формулы). При табличном задании первая строка таблицы содержит возможные значения случайной величины, а вторая - их вероятности:

х	х1	х2	…	хп
р	р1	р2	…	рт

(здесь и в дальнейшем х обозначена случайная величина, а через х₁, х₂, ..., х_п – ее возможные значения).

Так как в одном испытании случайная величина принимает одно и только одно возможное значение, события х = х₁, х = х₂, ..., Х = х_п образуют полную группу, поэтому сумма их вероятностей равна единице р₁ + р₂ + ... + р_п = 1.

Графическое изображение закона распределения получают построением многоугольника распределения в прямоугольной системе координат. По оси абсцисс откладывают значения Х, по оси ординат — р, строят точки (х_i, р_i ) и соединяют их отрезками.

Закон распределения непрерывной случайной величины задают функцией распределения F (х) (называемой также интегральной функцией распределения), определяющей вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е.

F (х) = р(Х < х),

В теории надежности оперируют наработкой (чаще временем) до возникновения отказа, т.е. некоторой случайной величиной τ, а отказ представляют как событие, состоящее в том, что τ В этом случае функция распределения F(t) наработки τ имеет физический смысл вероятности отказа объекта за время, меньшее t:

F (х) = р(τ < t),

Отказ объекта и его работоспособное состояние являются противоположными событиями, поэтому вероятность безотказной работы объекта в течение времени t может быть найдена по формуле P(t) = р (t ≥ t) = 1 — F(t).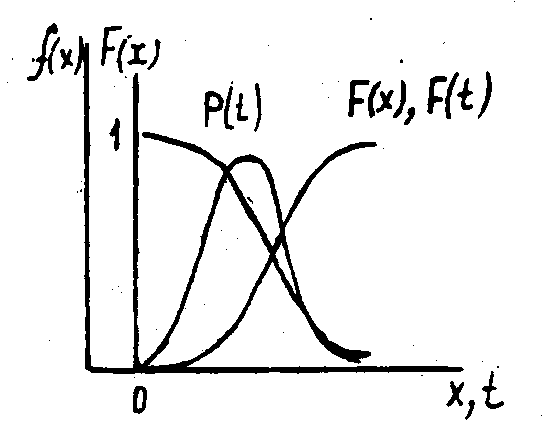



Рисунок 19. Кривые функций распределения F(х), F(t), надежности Р(t) и плотности распределения f (х)
Функция Р(t) называется функцией надежности.

Функция распределения обладает следующими свойствами:

1) значения функции распределения заключены на отрезке [0,1] 0≤F(х)≤1;

2) функция F(x) - неубывающая, т.е. F(x₂) ≥ F(x₁), если х₂ > х₁,

3) если возможные значения случайной величины принадлежат к интервалу (а, б), то: F(x) = 0 при х≤ а; F(x) = 1 при х ≥ б. Отсюда также следует, что F (-∞) = 0 (событие Х<∞ невозможное); F (+∞) = 1 (событие Х < + ∞ достоверное).

Для непрерывных случайных величин функция распределения непрерывна.

Функция распределения дискретной случайной величины имеет разрывы (скачки) в точках, соответствующих возможным значениям случайной величины; ее можно записать следующим образом:


Неравенство х_i<Х под знаком суммы показывает, что суммирование распространяется на все значения х_i, которые меньше Х. Следовательно, чтобы найти значение статистической функции распределения при данном Х достаточно подсчитать число результатов испытания, в которых значения х_i<Х, и разделить на общее число п результатов.

Наряду с функцией распределения для задания случайной величины применяют другую функцию, называемую плотностью распределения или плотностью вероятности (иногда ее называют дифференциальной функцией распределения). Эта функция играет весьма важную роль в теории надежности, так как по ее характеру можно судить о физической сущности и природе отказов.

Плотность распределения обладает следующими свойствами:

1) она является неотрицательной функцией f(х)≥0;

2) интеграл от плотности распределения в пределах от -∞ до +∞ равен единице:



Плотность распределения f(х) (рис. 19) является первой производной от функции распределения: f(x) = F'(х).

Как функция, так и плотность распределения полностью характеризуют случайную величину. Однако в ряде случаев пользуются менее полными, но более простыми числовыми характеристиками, дающими количественную оценку случайной величины. При расчетах надежности различных объектов в качестве числовых характеристик обычно рассматривают математическое ожидание и дисперсию.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности



Для непрерывных случайных величин математическое ожидание выражается формулой

,

Математическое ожидание приближенно равно среднему арифметическому значению случайной величины, которое определяется из выражения



где п — число наблюдений.

Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от ее математического ожидания .

Дисперсией случайной величины Х называется математическое ожидание квадрата соответствующей центрированной величины



Дисперсия характеризует степень рассеяния случайной величины относительно математического ожидания.

Дисперсию вычисляют по формулам:

для дискретных случайных величин

,

для непрерывных случайных величин



Для оценки рассеяния случайной величины используют также среднеквадратичное отклонение .

Для случайных функций, как и для случайных величин, вводятся характеристики, которые также являются функциями.

Математическим ожиданием случайной функции Х(t) называется неслучайная функция D_х(t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции М[Х(t)] =т_х(t).

Дисперсией случайной функции Х(t) называется неслучайная функция D_х(t), значение которой для каждого t равно дисперсии соответствующего сечения случайной функции



Внутренняя структура случайных функций, т.е. степень связи между сечениями описывается корреляционной функцией, которая представляет собой неслучайную функцию двух аргументов , , равную корреляционному моменту сечений, соответствующих каждой паре значений



При корреляционная функция обращается в дисперсию случайной функции:

,

Случайная функция Х(t) называется стационарной, если ее вероятностные характеристики (математическое ожидание, дисперсия и корреляционная функция) не зависят от t. Стационарные функции описывают различные стационарные процессы, протекающие во времени приблизительно однородно и имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний существенно не меняются с течением времени. Примерами таких процессов являются колебания усилия прокатки при установившемся процессе; погрешности показаний измерительного прибора и т.п. Каждый стационарный процесс можно рассматривать как продолжающийся во времени неопределенно долго и в качестве начала отсчета можно выбрать любой момент времени. Указанные особенности стационарных случайных процессов (функций) определяют условия, которым они должны удовлетворять: для этих функций математическое ожидание и дисперсия постоянны, т.е. m_х(t)=сопst, и D_х(t)= сопst, а корреляционная функция не зависит от положения t первого аргумента на оси абсцисс и определяется только разностью , т.е. является функцией только одного аргумента



Стационарная случайная функция называется эргодической или обладает эргодическим свойством, если каждая отдельная ее реализация достаточной продолжительности является эквивалентной множеству отдельных реализаций и при обработке опытных данных может заменить это множество. Для такой функции среднее по времени одного наблюдения достаточной продолжительности приближенно равно среднему по множеству наблюдений.

В теории надежности случайные функции применяют для моделирования случайных процессов переходе объекта из одного состояния в другое в случайные моменты времени (например, переходы объекта из работоспособного состояния в состояние отказа, профилактики или восстановления и наоборот).

Поскольку число состояний объекта является конечным (т.е. таким, которое можно пронумеровать), переходы из одного состояния в другое происходят скачком и представляют собой случайный процесс со счетным множеством состояний и непрерывным временем.

Переходы рассматриваются как события, а совокупность их — как поток событий. Как поток событий в теории надежности рассматривается и поток отказов.

Поток событий называется стационарным, если вероятность появления того или иного числа событий за период с зависит только от продолжительности этого периода и не зависит от момента его начала.

Поток событий называется без последствия, если для любых неперекрывающихся периодов времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

Поток событий называется ординарным, если вероятность одновременного появления двух и более событий пренебрежимо мала по сравнению с вероятностью одного события (события - редки). Если поток событий стационарен, ординарен и не имеет последствия, он называется простейшим или стационарным пуассоновским потоком. Для простейшего потока число событий, происходящих за период τ, распределено по закону Пуассона и вероятность того, что за этот период произойдет m событий равна

,

где λ — плотность потока (среднее число событий в единицу времени).

Простейший поток играет важную роль в теории надежности, так как потоки отказов многих сложных систем, состоящих из большого числа элементов, отказы которых независимы, хорошо описываются законом Пуассона. Кроме того, даже при потоке, отличающемся от простейшего, при замене его простейшим с той же плотностью, получаемые решения отличаются от точных всего на 3-5%, что вполне приемлемо для практических целей.

Если поток является ординарным и без последствия, но имеет переменную плотность, он называется нестационарным пуассоновским потоком.

Нарушение условий стационарности или наличие последствия приводит к тому, что поток становится не простейшим. В теории надежности важную роль играют не простейшие потоки Эрланга, которые образуются путем исключения событий из простейшего потока таким образом, что сохраняется каждое k-тое событие; в этом случае образуется поток Эрланга k-того порядка. При k = 1 поток Эрланга — простейший, при k→∞ поток приближается к регулярному потоку с постоянным интервалом между событиями .

Для потока Эрланга число событий за период τ (т.е. вероятность того, что за этот период произойдет k событий) распределено по закону



где λ – плотность (интенсивность) исходного простейшего потока.

Плотность событий потока Эрланга . Математическое ожидание времени между событиями .

Дисперсия времени между событиями .

Из последних двух выражений определяются значения и k при замене любых произвольных функций распределения на эквивалентные им функции Эрланга путем подстановки средних значений и дисперсии времени между событиями для произвольных функций.
Лабораторные занятие №4