УМКД Надежность. Надежность УМКД 2017 (1). Учебнометодический комплекс дисциплины Надежность технологических машин

• Название: Учебнометодический комплекс дисциплины Надежность технологических машин
• Анкор: УМКД Надежность
• Дата: 23.01.2022
• Размер: 1.75 Mb.
• Имя файла: Надежность УМКД 2017 (1).doc
• Тип: Учебно-методический комплекс; #339787
• страница: 7 из 16

3. Основные типы структур сложных систем. Если представить себе систему, у которой все элементы имеют параметры только 1-го типа (Х₁), т.е. влияющие на работу лишь самого элемента, то надежность такого элемента может быть определена независимо от других частей системы.

Анализ надежности таких систем, как правило, более прост поскольку элементы работают как независимые и для обеспечения надежность системы необходимо и достаточно обеспечить безотказную работу каждого элемента в отдельности. Заменой отказавшего элемента восстанавливается работоспособность системы.

Однако для машиностроения более характерно наличие таких выходных параметров отдельных элементов, которые участвуют в формировании выходных параметров всего изделия. В этом случае элементы нельзя считать независимыми и для каждого из них определять показатели надежности. Здесь необходимо рассматривать систему или подсистему в целом и учитывать как участие каждого элемента в формировании выходного параметра системы, так и их взаимное влияние на работоспособность.

Для сложных систем характерно комбинированное построение структуры, когда надежность отдельных подсистем может рассматриваться независимо.

Таким образом, с позиций надежности, могут быть следующие структуры сложных систем:

Расчлененные – у которых надежность отдельных элементов может быть заранее определена, так как отказ элемента можно рассматривать как независимое событие;

Связанные – у которых отказ элементов является зависимым событием, связанным с изменением выходных параметров всей системы;

Комбинированные – состоящие из подсистем со связанной структурой и с независимым формированием показателей надежности для каждой из подсистем.

Для современных технических систем наиболее характерна комбинированная структура.

4. О надежности сложных систем. Анализ надежности сложных систем имеет свои специфические особенности. Влияние различных отказов и снижение работоспособности элементов изделия по разному скажутся на надежности всей системы.

При анализе надежности сложного изделия все его элементы и детали целесообразно разделить на следующие группы.

1. Элементы, отказ которых (нарушение ТУ) практически не влияет на работоспособность изделия. Отказы этих элементов могут рассматриваться изолированно от системы. Часто говорят не об отказах, а о неисправном состоянии таких элементов.

2. Элементы, работоспособность которых за рассматриваемый промежуток времени практически не изменяется, т.е. Р(t=Т)→1 (станины и корпусные детали, гидростатические подшипники, малонагруженные элементы с большим запасом прочности).

3. Элементы, ремонт или регулировка которых возможна при работе изделия или во время остановок, не влияющих на его эффективность.

4. Элементы, отказ которых приводит к отказам изделия.

Таким образом, рассмотрению подлежат лишь элементы последней группы. Если к этому добавить, что элементы по требованиям к надежности должны быть подразделены на категории то, как правило, имеется ограниченное число элементов, которые в основном и определяют надежность изделия и служат объектом рассмотрения. Эти элементы и подсистемы выявляются при рассмотрении так называемой структурной схемы параметрической надежности.

Другая особенность работы сложных систем заключается в следующем. Предположим, что надежность всех элементов системы обеспечена, т.е. все их параметры находятся в пределах, установленных ТУ и их безотказность Р(t) →1. Означает ли это, что и вся система будет работоспособна? Обычно считают, что да. Однако это верно лишь для расчлененных структур. Как правило, безотказность работы элементов – необходимое, но не достаточное условие для безотказной работы всей системы.

Во-первых, большую роль играют взаимосвязи, когда работоспособные элементы оказывают побочные воздействия на другие элементы и могут вывести их из строя.

Во-вторых, малые изменения параметров каждого из элементов (в пределах нормы) могут дать такое сочетание, которое неблагоприятно отразится на работоспособности изделия. Это возможно из-за сложности функционирования системы и в результате того, что допуски на параметры ее элементов, как правило, назначаются без учета всех возможных взаимодействий и взаимовлияний.

Таким образом, специфика оценки надежности сложных изделий заключается в том, что в сложных системах большую роль играют связи между ее элементами.

Другая особенность оценки надежности сложных систем заключается в трудности, а иногда и невозможности применения к системе в целом статистических методов анализа.

5. Эффективность системы. В связи с тем, что функционирование сложной системы связано с выполнением разнообразных задач в неодинаковых условиях эксплуатации, бывает трудно определить, является ли возникшее изменение выходных параметров машины отказом. В одних условиях работы эти изменения не повлияют на работоспособность изделия, в других может произойти снижение производительности, точности, скорости и других показателей, характеризующих эффективность работы машины. Машина может, как правило, функционировать и при возникновении параметрических отказов.

Поэтому в ряде случаев говорят не об отказе машины, а о снижении ее эффективности в процессе эксплуатации.

С позиции надежности понятие «эффективность изделия» необходимо в первую очередь для анализа способности системы функционировать во всем диапазоне возможных условий и режимов и установления предельных значений изменения выходных параметров сложной системы. Заказчик, эксплуатирующий сложное изделие, должен учитывать требования к ее выходным параметрам исходя из той эффективности, которая удовлетворяет его потребности.

Выход любого из параметров за установленные пределы будет являться параметрическим отказом, а оценка последствий данного отказа определит допустимое значение вероятности безотказной работы /Л.1, Л.2/.

Контрольные вопросы:

1. 
   Факторы, отрицательно влияющие на надежность сложных систем.
   
2. 
   Факторы, положительно влияющие на надежность сложных систем.
   
3. 
   Определение элемента сложной системы.
   
4. 
   Анализ надежности сложных систем.
   

Лекция 7. Тема: Прогнозирование надежности (вероятностные связи)

1. Методы прогнозирования.

2. Схема прогноза параметрической надежности машины.

3. Применение метода Монте-Карло для прогнозирования надежности.

4. Возможности метода статистического моделирования.

5. Оценка экстремальных ситуаций.
1. Методы прогнозирования. Прогнозирование отличается от расчета системы тем, что решается вероятностная задача, в которой поведение сложной системы в будущем определяется лишь с той или иной степенью достоверности и оценивается вероятность ее нахождения в определенном состоянии при различных условиях эксплуатации. Применительно к надежности задача прогнозирования сводится в основном к предсказанию вероятности безотказной работы изделия Р(t) в зависимости от возможных режимов работы и условий эксплуатации. Качество прогноза в большой степени зависит от источника информации о надежности отдельных элементов и о процессах потери ими работоспособности. Для прогнозирования в общем случае применяются разнообразные методы с использованием моделирования, аналитических расчетов, статистической информации, экспертных оценок, метода аналогий, теоретико-информационного и логического анализа и др.

Обычно прогнозирование, связанное с применением математического аппарата называется аналитическим. Специфика прогнозирования надежности заключается в том, что при оценке вероятности безотказной работы Р(t) эту функцию в общем случае нельзя экстраполировать. Если она определена на каком-то участке то за его пределами ничего о функции Р(t) сказать нельзя. Поэтому основным методом для прогнозирования надежности сложных систем является оценка изменения его выходных параметров во времени при различных входных данных, на основании чего можно сделать вывод о показателях надежности при различных возможных ситуациях и методах эксплуатации данного изделия (рис. 8).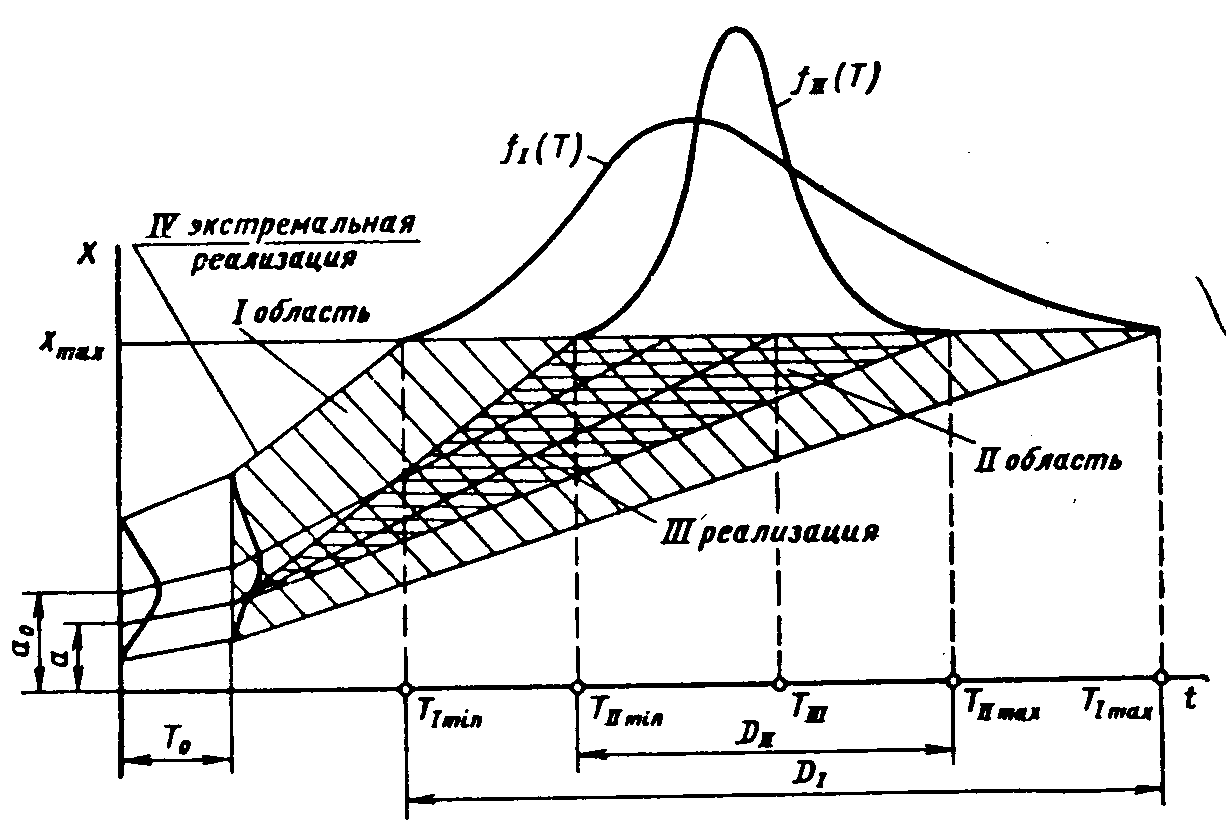



Рисунок 8. Области прогнозирования надежности
2. Схема прогноза параметрической надежности машины. Опираясь на общую схему потери машиной работоспособности можно представить три основных задачи по прогнозированию надежности.

1. Прогнозируется поведение всей генеральной совокупности данных машин, т.е. учитывается как вариация исходных характеристик машины, так и возможных условий ее эксплуатации.

2. Прогнозируется поведение конкретного образца машины, т.е. начальные параметры машины становятся неслучайными величинами, а режимы и условия эксплуатации машины могут изменяться в определенном диапазоне. В этом случае область состояний сужается (область ІІ) и становится подмножеством множество І.

3. Прогнозируется поведение данной машины в определенных условиях эксплуатации при постоянных режимах работы. В этом случае необходимо выявить реализацию случайного процесса ІІІ, которая соответствует заданным условиям работы.

Таким образом, если в первых двух случаях необходимо предсказать возможную область существования выходных параметров и оценить вероятность их нахождения в каждой зоне данной области, то в третьем случае ответствует неопределенность в условиях работы изделия, и прогноз связан лишь с выявлением тех закономерностей, которые описывают процесс изменения выходного параметра во времени.

Точность прогнозирования зависит от ряда факторов. Во-первых, от того, насколько принятая схема потери машиной работоспособности отражает объективную действительность. Во-вторых, насколько достоверны сведения о режимах и условиях предполагаемой работы изделия, а также о его начальных параметрах.

При прогнозировании надежности изделия на стадии проектирования имеется наибольшая неопределенность (энтропия) в оценке возможных состояний изделия. Однако методический подход к решению этой задачи остается общим.

В рассматриваемом случае он заключается в использовании в качестве основы для оценки вероятности безотказной работы изделия соответствующих моделей отказов состоит из следующих этапов.

1. Определение начальных параметров изделия (а_о; σ_а), как функции технологического процесса изготовления машины. Это связано с изменениями в пределах допуска размеров деталей, свойств материалов, качества сборки и других показателей. Значения начальных параметров могут зависеть также от режимов работы машины.

2. Установление предельно допустимых значений выходных параметров.

3. Оценка расчетным путем изменения выходных параметров в течение межналадочного периода Т_о (σ_в, σ_в , σ_с ;а_с) с учетом аналогичных характеристик у прототипа путем испытания при наличии опытного образца или путем учета установленных стандартом нормативов на параметры машины.

4. Оценка влияния процессов старения (γ) на выходные параметры изделия на основании физических закономерностей отказов с учетом их стохастической природы.

5. Оценка спектров режимов работы (нагрузок, скоростей и условий эксплуатации), которые отражают возможные условия эксплуатации и определяют рассеивание скоростей изменения выходных параметров (σ_х).

6. Расчет вероятности безотказной работы машины по каждому из параметров в функции времени.

7. При получении информации об эксплуатации изделия, для которого был сделан прогноз, производится сравнение действительных и расчетных данных и анализ причин их расхождения.

В зависимости от поставленной задачи должны быть выявлены области І и ІІ или оценена реализация ІІІ (см.рис.8), т .е. получены законы распределения f₁ (Т) или f₁₁ (Т), или соответственно Р₁ (Т) или Р₁₁ (Т), отражающие диапазоны рассеивания сроков службы для всей генеральной совокупности(D₁) или для данной машины (D₁₁). Если условия эксплуатации для данного образца жестко заданы, прогнозируется срок службы (наработка до отказа) Т₁₁₁.

3. Применение метода Монте-Карло для прогнозирования надежности. Для прогнозирования поведения сложной системы с успехом может применяться метод статистического моделирования (статистических испытаний), который получил название метода Монте-Карло.

Основная идея этого метода заключается в многократном расчете параметров на некоторой формализованной схеме, являющейся математическим описанием данного процесса (в нашем случае – процесса потери работоспособности).

При этом для случайных параметров, входящих в формулы, перебираются наиболее вероятные их значения в соответствии с законами распределения.

Таким образом, каждое статистическое «испытание» заключается в выявлении одной из реализаций случайного процесса, так как подставляя, хотя и случайным образом, выбранные, по зафиксированные аргументы, получаем детерминированную зависимость, которая описывает данный процесс при принятых условиях. Многократно повторяя испытания по данной схеме (что практически возможно в сложных случаях лишь с применением ЭВМ), получим большое число реализаций случайного процесса, которое позволит оценить ход этого процесса и его основные параметры.

4. Возможности метода статистического моделирования. Прогнозирование надежности методом Монте-Карло позволяет вскрыть статистическую природу провес влияния отдельных факторов. Например, для рассмотренной задачи можно сделать расчет, насколько повысится вероятность безотказной работы, если проведен ряд мероприятий по уменьшению давлений в зоне трения (изменена конструкция узла), уменьшено значение коэффициента k (применен новый материал), сужен диапазон режимов работы машины (изменены параметры законов f(P) и f(υ). Специфика применения метода статистического моделирования для расчета надежности заключается в том, что если обычно при статистическом моделировании сложных систем искомыми величинами являются средние значения характеристик, то здесь нас интересует область крайних реализации (значений близких к γ_max), так как именно они определяют значения Р (Т).

Поэтому для оценки надежности ответственных изделий важное значение приобретает исследование аварийных и экстремальных ситуаций, когда выявляются реализации процесса с наибольшей скоростью изменения выходных параметров γ_{Х max} .

5. Оценка экстремальных ситуаций. При прогнозировании надежности особое значение приобретает выявление крайней границы области состояний изделия, так как именно она определяет его близость к отказу. Эта граница формируется за счет реализаций, которые имеют наибольшие значения скорости процесса γ_Х. Хотя вероятность их появления мала (она соответствует вероятности отказа), их роль в оценке надежности изделия является основной. Такие реализации будем называть экстремальными.они могут быть двух типов: собственно экстремальные, как следствие наиболее неблагоприятного сочетания внешних факторов, но находящихся в допустимых пределах, и аварийные, которые связаны с нарушением условий эксплуатации или проявлением нарушений ТУ при изготовлении изделия.

Экстремальная реализация может быть выявлена как результат наиболее неблагоприятного сочетания факторов, влияющих на скорость изменения параметров γ_Х. Часто это предельные режимы, при которых существенно возрастают динамические нагрузки. Если для простых систем формулирование экстремальных условий, как правило, не вызывает трудностей (это наибольшие нагрузки, скорости, температуры), то для сложных систем необходимопровести исследования по выявлениютакого сочетания параметров, которое приведет к γ_{Х max}.

Аварийные ситуации связаны с двумя основными причинами. Во-первых, это возрастание внешних нагрузок и воздействий запределами установленными ТУ при попадании машины в недопустимые условия эксплуатации.для отдельных узлов и элементов машины такое положение может возникнуть из-за повреждения соседних малоответственных деталей, что повлияет на работу данного узла.

Во-вторых, возникновение аварийных ситуаций связано с нарушением ТУ на изготовление и сборку изделий. Производственные дефекты могут проявиться неожиданно и привести к отказу изделия /Л.3, Л.4/.

Контрольные вопросы:

1. 
   Чем отличается прогнозирование от расчета системы?
   
2. 
   Особенности трёх основных задач по прогнозированию надежности.
   

Лекция 8. Тема: Определение предельных и допустимых значений параметров технического состояния

1.Определение предельных и допустимых значений параметров технического состояния
В процессе оперативного управления работоспособностью техники наряду с общей статистической информацией необходимо индивидуальная информация, отражающая уровень технического состояния конкретного техника системы, агрегата, детали. Получение такой информации возможно путем непосредственного измерения параметров технического состояния данного транспорта значений с нормативами.

Любая техника представляет собой сложную техническую систему как известно, качественной мерой, позволяющей оценить состояние системы или ее элементов, а также проявление свойств системы, является параметр (показатель). С точки зрения оценки состояния системы и проявления ее свойств различают параметры структурные и выходные.

Каждый из элементов системы, которой является автомобиль или агрегат, и каждое простейшее сопряжение можно оценить с помощью одного или нескольких структурных выходных параметров. Система же оценивается по совокупности параметров, отражающих состояние отдельных элементов, сопряжений и их свойств.

В процессе эксплуатации автомобиля текущие значения параметров его состояния у_і изменяются от начальных или номинальных значений у_н до предельных у_n.

Формирование возможных состояний автомобиля определяется набором нормативных значений параметров состояния.

При эксплуатации изделия через определенную наработку значение параметра достигает предельной величины, при которой существенно ухудшаются технико-экономические показатели его использования или происходит отказ, момент наступления которого не поддается сколько-нибудь достоверному прогнозированию.

Изделие, у которого значение параметра достигло или превысило предельно допустимое значение, считается неисправным и находится в так называемом пред отказном состоянии.

Продолжение эксплуатации изделий в этой зоне обычно запрещено технической документацией (стандартами, техническими условиями заводов-изготовителей и т.п.), так как это приводит к аварийному отказу, ущерб о устранения которого значительно выше затрат на его предупреждение, или к резкому увеличению эксплуатационных расходов.

В связи с тем, что на практике контроль технического состояния проводится периодически через определенную наработку автомобиля, использование для управления техническим состоянием в качестве норматива предельно допустимого значения параметра не всегда возможно. Для этих целей в ряде случаев вводится новое понятие упреждающего значения параметра у_упр. Оно представляет собой ужесточенное предельно допустимое значение, при котором обеспечивается заданный либо экономически целесообразный уровень вероятности безотказной работы на предстоящей меж контрольной наработке. Нахождение значений параметра к моменту контроля в пределах между у_н и у_упр соответствует возможности эксплуатации автомобиля. Достижение значений в пределах между у_упр и у_пд свидетельствует о необходимости проведения предупредительных воздействий с затратами d, а пропуск значений параметров свыше у_п.д ведет к возникновению аварийного отказа, как правило, связанного со сходом автомобиля с линии или потерей рабочего времени и требующего проведения ремонта с затратами с>>d.

На основании анализа и классификации по методу назначения или определения нормативные значения параметров можно разбить на три группы.

К первой группе относятся нормативные значения, задаваемые на уровне государственных стандартов или других руководящих документов общегосударственного значения. Нормативы этой группы назначаются для параметров систем, обеспечивающих безопасность автомобиля и определяющих его влияние на окружающую среду. Эксплуатация автомобилей в любых условиях с отклонениями от этих параметров недопустимо.

К второй группе относятся нормативы параметров, изменение которых не зависит от условий эксплуатации автомобилей, а определяется только конструктивными и технологическими факторами, такими, как применяемые материалы, технология изготовления, форма и размеры и т.п.

К третьей группе относятся нормативы для параметров, на изменение которых в зависимости от наработки существенное влияние оказывают условия эксплуатации. В этом случае нормативные значения одного и того же параметра для автомобилей, работающих на различных видах перевозок, могут существенно (в 1,5 – 2 раза) отличаться.

Путем математической обработки статистических данных определяют закон распределения значений параметра f(у) и зависимости от вида ограничения и вероятности  определяют статистическую оценку предельно допустимого значения параметра.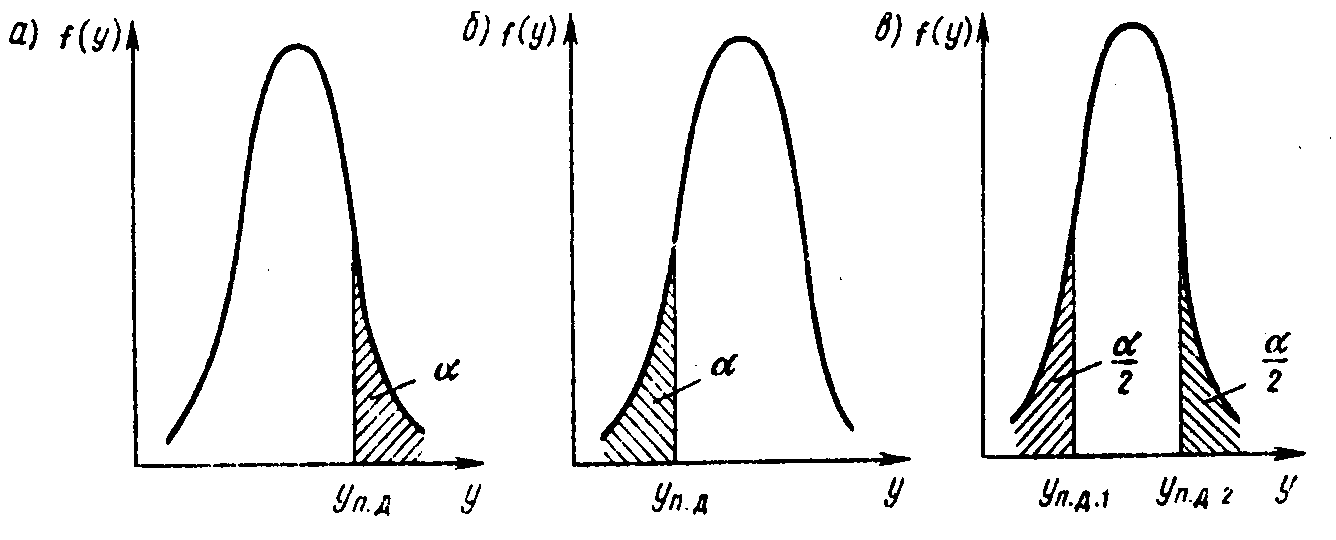



Рисунок 9. Определение предельно допустимого значения параметра у_п.д. на основе толерантных границ
Если параметр имеет одностороннее ограничение сверху, то в качестве предельно допустимого принимают значение у_п.д (рис.9,а), для которого

F(у) dу = 

Если параметр имеет одностороннее ограничение снизу то (рис.9 б)

F(у) dу = 

И, наконец, если параметр имеет двустороннее ограничение то предельно допустимых значений два – нижнее у_п.д1 и верхнее у _п.д2 (рис.9 в), для которых :

f(y)dy= α;

Необходимо иметь в виду что определяемое предельно допустимое значение параметра для одноименных объектов, входящих в выборку, будет иметь естественное рассеивание. В силу этого на граничных областях рассеивания, аппроксимируемого теоретическим законом распределения, одни и те же значения параметра могут соответствовать как исправному, так и неисправному состоянию. Поэтому уровень вероятности , определяющий назначение границы отнесения объекта к исправному или неисправному состояниям, определяется с учетом ошибок первого и второго рода, возможных при использовании данного параметра.

Под ошибкой первого рода понимают признание исправным, а под ошибкой второго рода понимается пропуск неисправности, когда неисправный объект признается годным к дальнейшей эксплуатации.

Ошибки первого рода приводят к неоправданным разборочно-сборочным и контрольным работам, простою автомобилей в ремонте. Ошибки второго рода приводят к возникновению аварийных линейных или дорожных отказов автомобилей или к значительным потерям за счет повышенного расхода топлива, увеличенной интенсивности изнашивания шин, к снижению срока службы аккумуляторных батарей /Л.1, Л.3/.