УМК КСЕ СПО. Учебнометодический комплекс по дисциплине концепции современного естествознания для студентов всех специальностей
 Скачать 3.72 Mb. Скачать 3.72 Mb.
|
Правила выполнения и оформления лабораторных работПри оформлении результатов лабораторных работ необходимо заполнить бланк отчета: Титульный лист: – название дисциплины; – тема лабораторной работы (номер, название); – сведения о студенте (ФИО, группа). Основная часть: – цель работы; – краткий конспект теории; – выполненные задания практической части (таблицы, описания, рисунки). – письменные ответы на контрольные вопросы. Выводы по проделанной работе. Лабораторная работа считается полностью выполненной, если она защищена по контрольным вопросам методических указаний. В отчет студенту преподаватель выставляет итоговую оценку за выполненную и защищенную работу. Лабораторная работа № 1. ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛ Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности. М  атериалы и оборудование: штатив с муфтой и лапкой, линейка, рулетка, шарик на нити, лист бумаги, секундомер. атериалы и оборудование: штатив с муфтой и лапкой, линейка, рулетка, шарик на нити, лист бумаги, секундомер.Теоретическая часть Эксперимент проводится с коническим маятником (рис.). Пусть шарик, подвешенный на нити, описывает окружность радиусом R. На шарик действуют две силы: сила тяжести и сила натяжения нити. Их результирующая создает центростремительное ускорение, направленное к центру окружности. Модуль ускорения можно определить, используя кинематику: Для определения ускорения необходимо измерить радиус окружности R и период Т обращения шарика по окружности. Центростремительное ускорение можно определить также, используя 2-й закон Ньютона: Направление координатных осей выберем так, как показано на рис. Спроецируем уравнение (2) на выбранные оси: Ох: Из уравнений (3) и (4) и из подобия треугольников получим: Таким образом, используя уравнения (1), (3) и (5), центростремительное ускорение можно определить тремя способами: Модуль составляющей Fх можно непосредственно измерить динамометром. Для этого оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности (рис.), и определяем показание динамометра. При этом сила упругости пружины уравновешивает горизонтальную составляющую Fх и равна ей по величине. В данной работе ставится задача убедится экспериментально, что числовые значения центростремительного ускорения, полученные тремя способами, будут одинаковыми (одинаковыми в пределах абсолютных ошибок). Практическая часть Задание 1. Определяем массу m шарика на весах. Результат взвешивания и инструментальную ошибку ∆m записать в таблицу 1. Задание 2. Вычерчиваем на листе бумаги окружность радиусом около 20 см. Измеряем данный радиус, определяем инструментальную ошибку и результаты записываем в таблицу 1. Задание 3. Штатив с маятником располагаем так, чтобы продолжение нити проходило через центр окружности. Задание 4. Взять нить пальцами у точки подвеса и вращать маятник так, чтобы шарик описывал такую же окружность как и окружность, начерченную на бумаге. Задание 5. Отсчитываем время t, за которое шарик совершает заданное число оборотов (к примеру, N = 30) и оцениваем ошибку ∆t измерения. Результаты записываем в таблицу 1. Задание 6. Определяем высоту h конического маятника и инструментальную ошибку ∆h. Расстояние h измеряется по вертикали от центра шарика до точки подвеса. Результаты записываем в таблицу 1. Задание 7. Оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности, и определяем показание динамометра F= Fх и инструментальную ошибку ∆F. Результаты записываем в таблицу:
Задание 8. Рассчитываем период Т обращения шарика по окружности и ошибку ∆Т: Задание 9. По формулам (6) рассчитываем значения центростремительного ускорения тремя способами и абсолютные ошибки косвенных измерений центростремительного ускорения. Контрольные задания 1. Как можно экспериментально определить период Т обращения шарика по окружности? 2. Что такое центростремительное ускорение, как его можно выразить через период обращения и через радиус окружности? 3. Что такое конический маятник. Какие силы действуют на шарик конического маятника? 4. Записать II закон Ньютона для конического маятника. 5. Какие три способа определения центростремительного ускорения предлагаются в данной лабораторной работе? Лабораторная работа № 2. ИЗУЧЕНИЕ СТАТИЧЕСКОГО РАВНОВЕСИЯ МЕХАНИЧЕСКИХ СИСТЕМ Цель работы: изучить динамику движения тел по наклонной плоскости; определить коэффициент трения скольжения для различных материалов. Материалы и оборудование: штатив, наклонная плоскость, набор тел, рулетка. Теоретическаячасть Пусть тело находится на наклонной плоскости, составляющей угол α с горизонтом. При увеличении угла α тело начинает скользить по наклонной плоскости. Подберем такой угол αо, при котором ускорение тела будет равно нулю, т.е. скольжение будет происходить с постоянной скоростью. Для этого случая сделаем рисунок, расставим на рисунке силы, действующие на тело, и запишем 2-й закон Ньютона для тела: 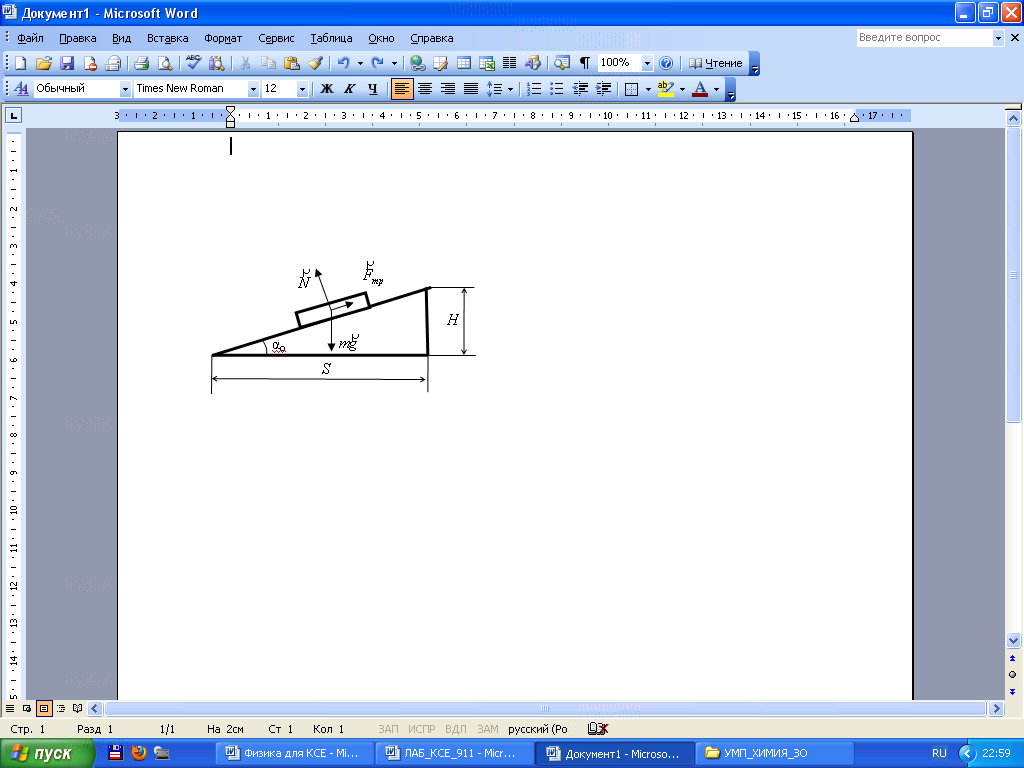 Ось x: Сила трения является силой трения скольжения и определяется по формуле: Подставляем (4) в (2) и переписываем систему уравнений: Ось x: Делим правые и левые части уравнений (5) и (6) друг на друга и получаем: Используя уравнение (7) можно экспериментально определить коэффициент трения скольжения. Практическая часть Задание 1. Установить деревянный брусок на наклонной плоскости. Задание 2. Увеличивая угол наклона плоскости добиться равномерного скольжения бруска по наклонной плоскости. Задание 3. С помощью рулетки измерить высоту H и длину S основания наклонной плоскости. Результаты измерений и инструментальные ошибки измерений занести в таблицу. Задание 4. Первые три пункта задания проделать для пластмассового бруска и для стального бруска. Результаты занести в таблицу. Задание 5. По формуле (7) рассчитать коэффициенты трения μ для трех тел и абсолютные ошибки Δμ. Результаты расчетов занести в таблицу:
Контрольные задания 1. Сформулируйте I и II законы Ньютона. 2. Запишите II закон Ньютона для тела, находящегося на наклонной плоскости в состоянии покоя и равномерно скользящего. Чему равна сила трения покоя, действующая на тело в этих случаях? 3. Что такое сила трения покоя и сила трения скольжения? Как определяются величины этих сил? 4. Расскажите, как в данной лабораторной работе экспериментально определяется значение коэффициента трения скольжения. 5. Как можно уменьшить коэффициент трения скольжения между двумя трущимися поверхностями? Лабораторная работа № 3. ИЗУЧЕНИЕ ЭВОЛЮЦИИ ОРГАНИЗАЦИОННЫХ СТРУКТУР МЕТОДОМ МОДЕЛИРОВАНИЯ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ Цель работы: изучение эволюции сложных потенциальных организационных структур на примере электростатического поля от электродов произвольной конфигурации методом аналоговой модели. Материалы и оборудование: блок питания, микроамперметр, вольтметр (тестер), щупы, зонды, специальный лабораторный макет. Специальный лабораторный макет или/и виртуальный лабораторный стенд исследования вариантов сложных систем; программное обеспечение: Gnuplot, kse.exe. Теоретическая часть Все тела в природе состоят из совокупности заряженных частиц, обычно электрически нейтральных. Электрический заряд может быть двух знаков − положительным, либо отрицательным. Суммарный заряд изолированной системы имеет свойства сохраняться (q1 +q2 +...+ qi = const), квантоваться, т.е. состоять из целого числа элементарных зарядов (зарядов электрона q = +/– Ne), а также взаимодействовать: (одноименные заряды отталкиваются, разноименные притягиваются), что можно доказать с помощью принципа наименьшего действия Томсона для потенциальных электростатических полей, создаваемых вокруг этих зарядов. Электрическое поле − вид материи, особое состояние пространства, которое создается заряженными частицами и действует на заряженные частицы. Электростатическое поле характеризуется напряженностью, определяемой по силе, действующей на единичный положительный заряд, помещенный в данную точку поля Электростатическое поле потенциально и работа, совершаемая полем при перемещении заряда в нем, равна разности потенциальных энергий в начальном и конечном положении заряда А=Wп1-Wп2=q(φ1-φ2). Поле характеризуется скалярной величиной φ − потенциалом φ = Wп /q (энергетическая характеристика). Силовая и энергетическая характеристика для потенциального электростатического поля связаны соотношением Если циркуляция вектора напряженности поля по замкнутому пути равна нулю, то поле потенциально. Для наглядности электрическое поле изображается силовыми линиями. Касательные к силовым линиям в любой точке совпадают с вектором напряженности, а по густоте этих линий на единичной площадке можно судить о том, на сколько поле сильнее или слабее в разных точках. Это свойство определяется теоремой Остроградского−Гаусса: «поток вектора напряженности через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности, деленной на электрическую постоянную вакуума» либо в дифференциальной форме: где div − операция векторного анализа, означающая расходимость вектора Е, p − объемная плотность заряда. Силовые линии электростатического поля начинаются на положительных зарядах, а заканчиваются на отрицательных, либо уходят в бесконечность, нигде не пересекаясь и не делая завихрений. О вихревых электрических полях будет сказано позднее. Другими словами, теорема Гаусса гласит о том, что источником электростатического поля являются электрические заряды. Помещенный в поле положительный заряд будет перемещаться по направлению силовых линий, а отрицательный − против. По виду силовых линий различают однородные поля (силовые линии расположены на одинаковом расстоянии и параллельны) и неоднородное − силовые линии имеют различную густоту и не параллельны. При рассмотрении полей пользуются принципом суперпозиции (наложения), являющимся следствием принципа независимого действия сил (каждая сила действует так, как будто нет действия других сил, т.е. их действие суммируется, накладывается) − этот принцип справедлив лишь для линейных систем. Для энергий принцип суперпозиции не выполняется. Для изучения явлений в электрических полях важно рассмотрение понятия электрический диполь − совокупность точечных зарядов, равных по величине, противоположных по знаку, находящихся на малом неизменном расстоянии друг от друга. При помещении диполя в однородное электрическое поле диполь будет вращаться в нем, т.к. на положительный и отрицательный заряд будут действовать одинаковые, но противоположно направленные силы, создавая вращающий момент, направленный вдоль оси вращения, перпендикулярной полю. Электростатическое поле можно изобразить с помощью эквипотенциальных поверхностей. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью d Следовательно, вектор Е в каждой точке поля направлен по нормали к эквипотенциальной поверхности. Исследование электростатического поля заключается в нахождении величины и направления напряженности в любой его точке, т.е. в построении силовых линий такого поля. Поэтому достаточно найти положение эквипотенциальных поверхностей, а затем построить силовые линии поля. В основе данной работы используется аналоговая модель непрерывной поглощающей среды, находящейся между электродами, форма которых задается преподавателем. Задача эксперимента заключается в измерении распределения потенциала поля от электродов и построение перпендикулярных эквипотенциальным линиям силовых линий поля. Поэтому для изучения поля электрических зарядов можно использовать поле тока в слабо проводящей среде (электропроводная бумага, покрытая, например графитом с нанесенной на ней масштабной сеткой для удобства позиционирования точек измерения потенциала). При его моделировании силовым линиям электростатического поля будут соответствовать линии тока, а поверхностям равного потенциала − поверхности равных напряжений. Напряжения различных точек модели измеряют вольтметром (тестером). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
