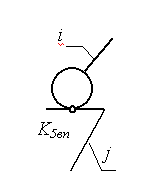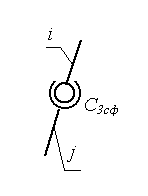Контрольная работа. Теория механизмов и машин - методич. 2019. Учебнометодическое пособие для выполнения контрольных работ по дисциплине Механика и детали машин
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
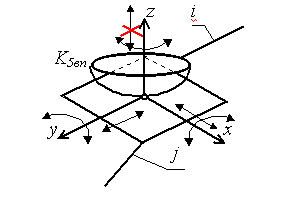
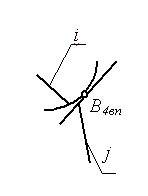
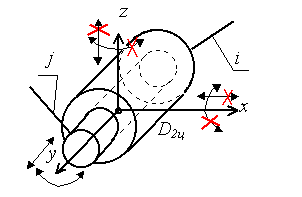
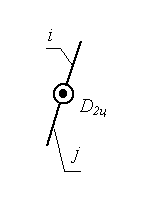
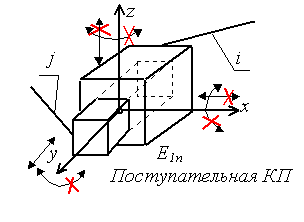
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» НАБЕРЕЖНОЧЕЛНИНСКИЙ ИНСТИТУТ Кафедра «Механика и конструирование» Теория механизмов и машин Учебно-методическое пособие для выполнения контрольных работ по дисциплине «Механика и детали машин» Набережные Челны 2019 УДК 631.8 Тазмеева Р.Н. Теория механизмов и машин: учебно – методическое пособие для практических занятий и самостоятельной работы студентов любой формы обучения. - Набережные Челны: НЧИ КФУ, 2019 – 48 с. Пособие содержит задания для выполнения контрольной и самостоятельной работы по теории механизмов и машин. Задания охватывают основные разделы курса: анализ рычажного механизма, структурное, кинематическое и силовое исследование плоских рычажных механизмов, приводятся примеры выполнения каждой задачи практической работы. Рецензент: к.т.н., доцент Н. Д. Ахметов Учебное пособие рассмотрено на заседании методического совета автомобильного отделения протокол № 8 от 19.05.2019 г. ОГЛАВЛЕНИЕ Анализ рычажного механизма Задача 1 Структурный анализ плоского рычажного механизма 4 Задача 2. Кинематический анализ механизмов 12 Задача 3. Силовой анализ механизмов 34 Рекомендуемая литература 47 АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА ЗАДАЧА 1. СТРУКТУРНЫЙ АНАЛИЗ ПЛОСКОГО РЫЧАЖНОГО МЕХАНИЗМА Для выполнения 1 задачи необходимо выполнить следующее: Ознакомиться с заданной схемой механизма, выявить стойку, входное, выходное и промежуточные звенья. Изобразить структурную схему механизма без соблюдения масштаба, пронумеровать все звенья (стойку обозначить цифрой 0), обозначить все кинематические пары прописными буквами (О, А, В, С.); Установить виды движения звеньев относительно стойки (абсолютные) и виды движения относительно друг друга. Составить таблицу кинематических пар, в которой указать номера звеньев, образующих каждую пару, название каждой пары и число её степеней свободы; Найти число степеней свободы механизма по формуле П.Л. Чебышева; Выделить начальное звено 1 и стойку 0, изобразив их отдельно; Оставшуюся кинематическую цепь разложить на структурные группы (группы Ассура), изобразив их отдельно. Указать класс и вид каждой структурной группы. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАЧИ 1 Рассмотрим основные термины. Звено механизма - твердое тело, входящее в состав механизма. Звено может содержать одну или несколько деталей, соединенных жестко между собой. Стойка - неподвижное звено механизма. Входное звено - звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходное звено-звено, совершающее движение, для выполнения которого предназначен механизм. Кинематическая пара - соединение двух соприкасающихся звеньев, допускающее их относительное движение. Элемент кинематической пары - совокупность поверхностей, линий и отдельных точек звена, по которым оно соприкасается с другим звеном. В высших кинематических парах элементом соприкосновения является линия или точка. В низших кинематических парах элементом соприкосновения является поверхность. Числом степеней свободы механической системы называется число независимых параметров, определяющих положение системы. По числу степеней свободы в относительном движении звеньев кинематические пары делятся на одно -, двух -, трех -, четырех и пяти подвижные, которые налагают на относительное движение звеньев соответственно пять, четыре, три, две и одну связь. Изображения и характеристики некоторых кинематических пар приведены в таблице 1. Таблица 1.1 - Классификация кинематических пар по числу связей и по подвижности
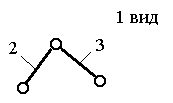
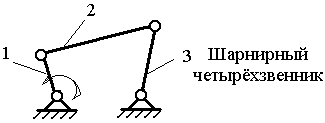
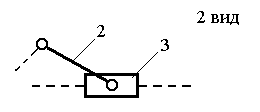
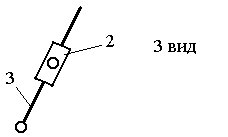
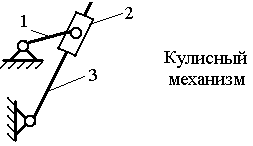
Примечание: Стрелки у координатных осей показывают возможные угловые и линейные относительные перемещения звеньев. Если стрелка перечеркнута, то данное движение в КП запрещено (т.е. на данное относительное движение наложена связь). Число степеней свободы пространственного механизма без избыточных связей определяют по формуле А.П. Малышева: W = 6n – 5p1 – 4p2 – 3p3 – 2p4 – p5 где п - число подвижных звеньев; р1 - число одноподвижных кинематических пар; р2 - число двух подвижных кинематических пар; р3 - число трёх подвижных кинематических пар; р4 - число четырёх подвижных кинематических пар; р5 - число пятиподвижных кинематических пар. Число степеней свободы плоского механизма определяют по формуле П.Л. Чебышева: W = 3п - 2р5 –р4. Рычажные механизмы содержат только низшие кинематические пары. В состав рычажных механизмов могут входить следующие звенья. Кривошип - звено, которое может совершать полный оборот вокруг стойки. Коромысло - звено, образующее вращательную пару со стойкой и не способное проворачиваться на полный оборот. Шатун - звено, не входящее в кинематическую пару со стойкой. Ползун - звено, образующее поступательную пару со стойкой. При изображении механизма на чертеже применяют структурную схему с использованием условных изображений звеньев без соблюдения их размеров и кинематическую схему с соблюдением размеров звеньев, необходимых для кинематического исследования. Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы, не имеющие избыточных связей и местных подвижностей состоят из первичных механизмов и структурных групп Ассура. Структурный анализ плоских рычажных механизмов по Ассуру Условие существования любой структурной группы описывается формулой: Все структурные группы принято разделять на классы – со 2-го по 4-й. Таблица 1.2- Классификация структурных групп 2 класса
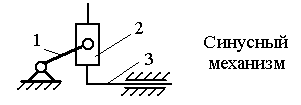
Примечание. 1 – ведущее звено; 2 и 3 – звенья, образующие структурную группу. Для определения класса механизма его расчленяют на структурные группы, начиная с конца механизма. За начало механизма принимают ведущее звено (начальный механизм). От конца механизма отделяются поочерёдно простейшие структурные группы до тех пор, пока не останется лишь механизм 1-го класса (начальный механизм, их может быть несколько). По классу структурных групп определяют класс механизма. Количество начальных механизмов равно величине W. Пример структурногоанализа рычажного механизма 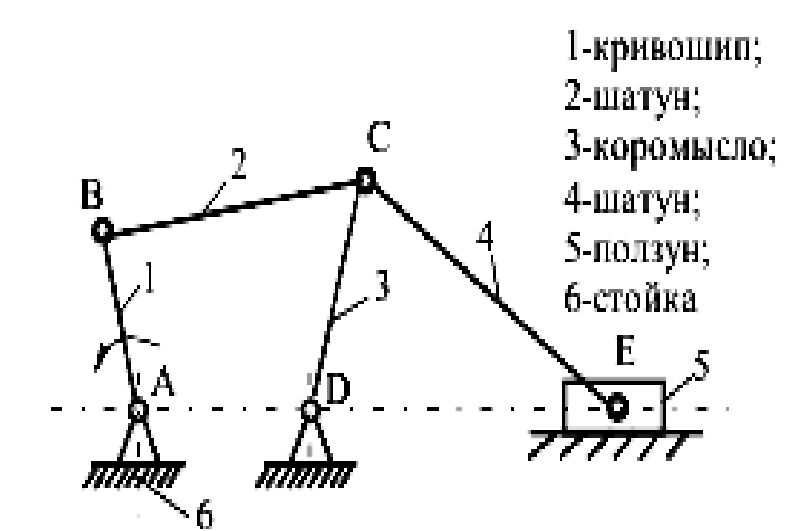 Рисунок 1.1 – схема механизма качающегося транспортера Начальным звеном является кривошип 1, выходным звеном - ползун 5.Число подвижных звеньев в этом механизме n = 5, число кинематических пар пятого класса Р5 = 7 (в точке С шарнирно соединены три звена, поэтому здесь две вращательные кинематические пары), пар четвертого класса (двух подвижных) нет (Р4=0). Следовательно, степень подвижности механизма W=3n-2Р5-Р4=3·2·7 = 1. Начальный механизм состоит из начального звена 1 и стойки 6. 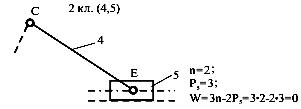 При разложении механизма на группы Ассура первой выделяем двух- поводковую группу, состоящую из звеньев 4 и 5. При разложении механизма на группы Ассура первой выделяем двух- поводковую группу, состоящую из звеньев 4 и 5.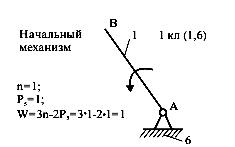  Из оставшегося четырехзвенника АВСD выделяем двухповодковую группу Ассура, состоящую из звеньев 2 и 3 (СД и ВС). Обе отсоединенные группы Ассура являются группами второго класса. Записываем структурную формулу механизма: 1 кл. (1,6) → 2 кл. (2,3) → 2 кл. (4,5) Механизм относится к второму классу, так как обе группы Ассура являются группами второго класса, и групп более высокого класса в этом механизме нет. Варианты заданий к задаче 1. 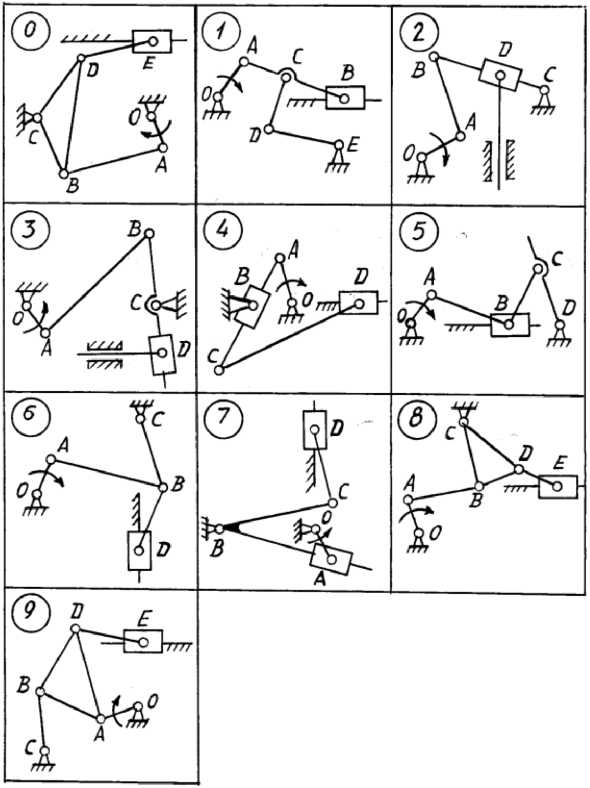 ЗАДАЧА 2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ Для выполнения 2 задачи необходимо выполнить следующее: 1. Определить кинематические характеристики звеньев: перемещение; скорость; ускорение; траектория движения; функция положения при известных законах движения входных (ведущих) звеньев. 2. Оценить кинематические условия работы рабочего (выходного) звена. 3. Определить необходимые численные данные для проведения силового, динамического, энергетического и других расчётов механизма. Исходные данные: 1. Кинематическая схема механизма. 2. Размеры и иные геометрические параметры звеньев (но только такие, которые не изменяются при движении механизма). 3. Законы движения входных звеньев (или параметры движения, например, угловая скорость и угловое ускорение входного звена в выбранном для анализа положении механизма). МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАЧИ 2 Кинематический анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. По сравнению с синтезом анализ механизма широко используется в практике. Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев. Для механизмов, подчиняющихся классификации Л. В. Ассура, порядок кинематического анализа определяется формулой строения: , вначале находят параметры движения начальных механизмов и затем – структурных групп в порядке следования их в формуле строения. Графоаналитический метод кинематического анализа Графоаналитический метод называют методом планов скоростей и ускорений. Задача о положениях решается графическим методом, то есть построением нескольких совмещённых планов механизма в выбранном масштабе длин. Задачи о скоростях и ускорениях решаются построением планов скоростей и ускорений звеньев механизма при определённых (заданных) положениях ведущего звена на основе заранее составленных векторных уравнений скоростей и ускорений звеньев механизма. Преимущество этого метода по сравнению с графическим в том, что он менее трудоёмок, так как позволяет определять скорости и ускорения (их величину и направление) на одном плане скоростей или плане ускорений для множества точек механизма. Недостатком метода является то, что требуется построить планы скоростей и ускорений для нескольких положений механизма (если необходимо определять скорость и ускорение при различных положениях механизма и его звеньев). Следует помнить, что в основе построения планов скоростей и ускорений лежат законы плоскопараллельного движения. Согласно этим законам: 1. План скоростей (а также план ускорений) получается в результате графического решения векторных уравнений для определения скоростей (ускорений) точек в плоскопараллельном движении; 2. Векторы абсолютных скоростей точек (при рассмотрении их движения относительно неподвижного звена) изображаются исходящими из полюса плана, а направление совпадает с касательными к траектории движения. Векторы относительных скоростей точек (при их движении относительно подвижных точек) изображаются отрезками, соединяющими концы соответствующих векторов абсолютных скоростей; 3. Длина векторов относительных скоростей пропорциональна длине тех участков звеньев, которые являются радиусами вращения точек в их относительном движении. Это положение, известное под названием теоремы подобия, облегчает определение скоростей многих точек, лежащих на звеньях плоскопараллельного и вращательного движения. При построении планов механизма, а также планов скоростей и ускорений пользуются масштабным коэффициентами, показывающими, сколько единиц той или иной величины приходится на один миллиметр отрезка, изображающего эту величину. Масштабный коэффициент обозначается буквой К с соответствующим индексом: Kl-масштабный коэффициент длин, м/мм; Кv-масштабный коэффициент линейных скоростей точек, м/с ∙мм; Ка-масштабный коэффициент линейных ускорений точек, м/с2 ·мм. Масштабные коэффициенты определяются следующим образом: Kl = lAB/AB м/мм; Кv = VB/рВ м/с∙мм; Ка = аВ/πв м/с2∙мм. где lАВ - действительная длина звена АВ, м; AВ - длина отрезка, изображающего данное звено на плане, мм; VВ - модуль скорости точки В, м/с; Рв - длина отрезка, изображающего скорость этой точки на плане скоростей, мм; аВ - модуль ускорения точки В, м/с2; πв - длина отрезка, изображающего ускорение этой точки на плане ускорений, мм. Иногда применяются вместо масштабных коэффициентов масштабы, под которыми понимают отношение отрезков на планах в миллиметрах к числовому значению изображаемых величин. Обозначаются масштабы буквой µ с соответствующим индексом: l - масштаб длин, мм/м; µV - масштаб линейных скоростей, мм/ (м с-1); µa - масштаб линейных ускорений, мм/(мс-2). |