Методичка по вычислительной математике. Методы вычислительной математики для решения задач информационно. Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
2.2 Лабораторная работа 2. « Решение нелинейных уравнений»Цель: сформировать навыки решения нелинейных уравнений численными методами. Порядок выполнения работы Теоретическая часть 1.1 Основные определения 1) Пусть задана непрерывная функция fx и требуется найти корни уравнения fx=0 (1)на всей числовой оси или на некотором интервале 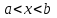 . .Всякое значение 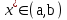 , удовлетворяющее условию , удовлетворяющее условию 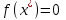 , называется корнем уравнения (1), а способ нахождения этого значения , называется корнем уравнения (1), а способ нахождения этого значения 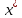 - решением уравнения (1). - решением уравнения (1). Численное решение уравнения проводится в два этапа: 1 этап: отделение корней уравнения. 2 этап: уточнение интересующих корней с заданной точностью ε. Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит. Уточнение корня – это вычисление интересующего корня с заданной точностью . 2) Расчетные формулы методов решения нелинейного уравнения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| N | f(x) | g(x) | [a, b] |
| 2.1.1 | | | |
| 2.1.2 | | | |
| 2.1.3 | | | |
| 2.1.4 | | | |
| 2.1.5 |  | | |
| 2.1.6 | | | |
| 2.1.7. | | | [5,25] |
| 2.1.8 | | | [0.1,10] |
| 2.1.9 | | | [0.1,2] |
| 2.1.10 | | | |
| 2.1.11 | | | |
| 2.1.12 | | | |
| 2.1.13 | | | [0,3] |
| 2.1.14 | | | [0,2] |
| 2.1.15 | | | [0,3] |
| 2.1.16 | | | |
| 2.1.17 | | | |
| 2.1.18 | | | |
| 2.1.19 | | | |
| 2.1.20 |  | | |
| 2.1.21 | | | |
| 2.1.22 | | | [0.001,3] |
| 2.1.23 | | | [0.1,35] |
| 2.1.24 | | | [0.01,3] |
| 2.1.25 |  | | |
| 2.1.26 | | | [-0.5,1.5] |
| 2.1.27 | | | [-1.5,0] |
| 2.1.28 | | | [1,3] |
| 2.1.29 | | | [0,3] |
| 2.1.30 | | | [0,5] |
Таблица к задаче 2.2 Таблица к задаче 2.3
| N | f(x) | Найти корень | N | f(x) |
| 2.2.1 | | отрицательный | 2.3.1 | |
| 2.2.2 | | положительный | 2.3.2 | |
| 2.2.3 | | положительный | 2.3.3 | |
| 2.2.4 | | наибольший. по модулю | 2.3.4 | |
| 2.2.5 | | все корни | 2.3.5 | |
Таблица к задаче 2.4
| f(x) | |||||
| N | | | | | |
| 2.4.1 | 4.545004 | -3.055105 | -18.06895 | 4.002429 | 4.722482 |
| 2.4.2 | -2.656764 | -3.406111 | 10.89372 | -1.752935 | -3.423612 |
| 2.4.3 | -4.556062 | 2.93309 | 9.274868 | -10.32081 | 0.422098 |
| 2.4.4 | 7.809249 | 16.28542 | -2.771356 | -27.95304 | -11.33921 |
| 2.4.5 | -13.0072 | 60.24546 | -122.0716 | 105.6798 | -30.19201 |
Таблица к задаче 2.5
| N | f(x) | [a, b] |
| 2.5.1 | | [0.8,1.2] |
| 2.5.2 | | [0.3,0.7] |
| 2.5.3 | | [0.5,1] |
| 2.5.4 | | [0,1] |
| 2.5.5 | | [0,0.7] |

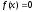 .
.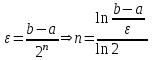
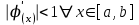
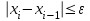
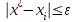
 , n=0,1,…
, n=0,1,…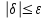 ,
,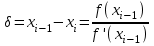 −корректирующее приращение или поправка.
−корректирующее приращение или поправка.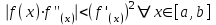
 , n=0,1,…;
, n=0,1,…;  , n=0,1,…
, n=0,1,… , n=0,1,…
, n=0,1,… , n=0,1,…, m=1,2,…
, n=0,1,…, m=1,2,… ,
,  =1.31811607652818,
=1.31811607652818,  =1.738244406014586
=1.738244406014586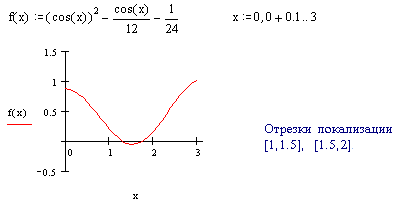



 , где в п. a) q=(M-m)/(M+m), в п. b)
, где в п. a) q=(M-m)/(M+m), в п. b)