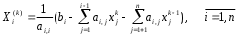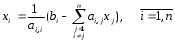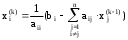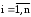Методичка по вычислительной математике. Методы вычислительной математики для решения задач информационно. Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||
| Крамера | | | | | |||||
| | | | | |||||
| | | | | |||||
| | | | |
|
|
| |||||||||||
| 1 |
|
|
|
|
| ||||||||
| 2 |
|
|
|
|
| ||||||||
| 3 |
|
|
|
|
| ||||||||
| 4 | 4.300 0.100 0.000 0.000 |
|
| 0.000 0.000 0.197 -1.600 | 2.663 2.778 2.533 1.928 | ||||||||
| 5 |
| 0.268 4.700 -0.150 0.000 |
| 0.000 0.000 0.274 2.900 | 4.032 4.313 4.235 3.797 | ||||||||
| 6 | 6.900 0.191 0.000 0.000 |
|
| 0.000 0.000 0.000 4.200 |
| ||||||||
| 7 | -8.200 0.234 0.000 0.000 |
| 0.000 5.600 -0.340 0.268 |
| 7.559 8.175 8.421 8.322 | ||||||||
| 8 |
| 0.422 8.601 0.315 0.000 |
| 0.000 0.000 0.496 6.803 | 9.719 10.500 10.915 10.978 | ||||||||
| 9 | 10.800 0.321 0.000 0.000 |
|
| 0.000 0.000 -6.060 8.100 | 12.143 13.089 13.674 13.897 | ||||||||
| 10 | -1.100 0.365 0.000 0.000 |
|
| 0.000 0.000 0.534 -0.570 |
| ||||||||
| 11 | 13.400 -0.408 0.000 0.000 |
| 0.000 -0.650 -11.600 0.546 |
| 17.782 19.593 19.974 20.528 | ||||||||
| 12 | 30.300 0.975 0.000 0.000 |
|
| 0.000 0.000 1.660 27.600 | 80.168 83.578 86.609 89.278 | ||||||||
| 13 | 0.161 0.109 0.000 0.000 |
| 0.000 -0.150 0.171 0.145 |
| 86.814 90.358 19.861 93.502 | ||||||||
| 14 | 22.500 0.714 0.000 0.000 |
|
| 0.000 0.000 0.124 19.800 | 45.802 48.261 50.343 52.4 | ||||||||
| 15 | 26.400 0.840 0.000 0.000 |
| 0.000 0.198 24.600 0.000 |
| 61.853 64.730 63.880 59.376 | ||||||||
2.5 Лабораторная работа 5. «Аппроксимация производных конечными разностями».
Цель: изучение основных методов аппроксимации производных с помощью конечно-разностных соотношений.. Численное дифференцирование на ЭВМ с помощью разностей сложных функций и функций заданных таблицей.
Порядок выполнения работы
Теоретическая часть
Основные определения
1) Аппроксимация производных конечными разностями. Производной функции y=f(x) называется предел:
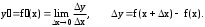
Для приближенного вычисления производной используется формула:
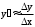 , где x - некоторое конечное число.
, где x - некоторое конечное число.Разностные соотношения, в которых разность между любыми значениями аргумента является конечной величиной, называются конечными разностями. Поэтому соотношение также называют аппроксимацией производной с помощью конечных разностей.
Пусть известны значения функции y0,y1,...,yi,...,yn, вычисленные или заданные таблицей в точках x0,x1,...,xi,...,xn. Точки x0,x1,...,xi,...,xn называются узлами, а разность между соседними значениями аргумента называется шагом hi=xi=xi-xi-1, i=1,...,n. Весь набор узлов называется сеткой. Если величина шага между узлами постоянна, то говорят, что узлы x0,x1,...,xi,...,xn образуют равномерную сеткой с шагом h.
Для вычисления производной yi в точке точки xi можно использовать левую разность:
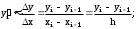
правую разность:
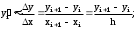
центральную разность:
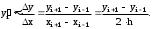
2) Погрешность численного дифференцирования. При численном дифференцировании с использованием приближенной формулы, естественно возникает погрешность: R(x,h)=y(x)-yh(x,h), где y(x) - точное значение производной, yh(x,h)- значение производной вычисленное по приближенной формуле при шаге h.
Величина погрешности зависит от точки x, в которой вычисляется производная, и от шага h, чем меньше шаг, тем естественно погрешность меньше. Обычно погрешность R(x,h) записывают одним из способов:

где, (x)hk- называется главной частью погрешности аппроксимации, т.к. в формуле это слагаемое при h<<1 будет гораздо больше второго, а величина k называется порядком погрешности или порядком точности аппроксимации относительно шага h.
С помощью разложения в ряд Тейлора получены следующие оценки погрешности для формул:
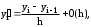 левая разность;
левая разность;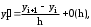 правая разность;
правая разность; 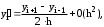 центральная разность.
центральная разность.Из этих формул следует, что центральная разность имеет самый высокий порядок точности, а именно, второй порядок по h.
3) Аппроксимирующие формулы для любого порядка точности. Аппроксимацию производных конечными разностями в общем случае можно рассматривать как замену производной от функции y=f(x) производной от аппроксимирующей функции (x), (x)f(x), где в качестве аппроксимирующей функции используется интерполяционный многочлен:
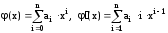 . Поэтому увеличивая степень интерполяционного многочлена n мы будем увеличивать порядок точности аппроксимации производной.
. Поэтому увеличивая степень интерполяционного многочлена n мы будем увеличивать порядок точности аппроксимации производной.С помощью интерполяционного многочлена Лагранжа при равномерном распределении узлов были получены следующие формулы для аппроксимации производной с помощью центральных разностей второго и четвертого порядка точности:
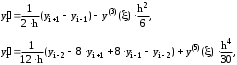
где, y(k)() - значение “к”-той производной в некоторой точке на отрезке [xi-2,xi+2].
В крайних точках таблицы или в крайних узлах нельзя использовать соотношения для центральных разностей. В этих точках используются односторонние формулы численного дифференцирования:
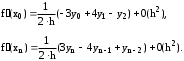
4) Выбор оптимального шага при численном дифференцировании. Полная погрешность численного дифференцирования определяется не только погрешностью используемой формулы численного дифференцирования, но и погрешность возникающей при вычислениях по этим формулам. Например, при вычисления по первой формуле абсолютная предельная погрешность будет равна:
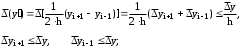
где y - абсолютная предельная погрешность вычислений значений функции y из-за ошибок округления.
Так как величина y является неустранимой погрешностью, то согласно определения абсолютного числа обусловленности для задачи численного дифференцирования имеем: =1/h, т.е. задача плохо обусловлена, т.к. при при h0 число обусловленности стремится к бесконечности.
Полная абсолютная погрешность вычисления производной R(yi) будет равна сумме погрешностей:
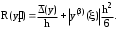
Первое слагаемое (погрешность вычислений) при уменьшении шага увеличивается, а второе слагаемое (погрешность самой формулы) уменьшается. Естественно будет такой шаг при котором полная погрешность будет минимальной., такой шаг называется оптимальным,
Оптимальный шаг hопт определяется из условия минимума R(yi), т.е. уравнения Rh(yi)=0, где значок h - говорит о том, что производная берется по h.
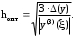
Естественно для каждой формулы численного дифференцирования будет своя формула для вычисления оптимального шага.
Если величина абсолютной предельной погрешности вычислений значений y определяется погрешностью округления ( машинным эпсилон ) (y)= y, то можем записать:
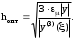
Обычно на практике полагают, что
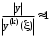 .
.5) Улучшение аппроксимации с помощью метода Рунге -Ромберга. Пусть y(x) - точное значение производной, а yh(x,h) -значение производной, вычисляемое по формуле численного дифференцирования, имеющей порядок точности к относительно шага h. Следовательно можем записать:
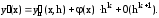
Запишем это же соотношение для шага h1=ph:
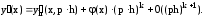
Вычитая
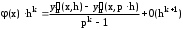 ,
, и подставляя, получаем
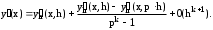
Формула позволяет по результатам двух расчетов производной с шагом h и шагом ph по одной и той же формуле, имеющей порядок точности k, найти ее уточненное значение с порядком точности k+1. Данный прием называется методом Рунге-Ромберга.
Контрольный пример
Вычислить с помощью центральных разностей второго порядка точности производную от функции, заданной дискретно:
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 |
| y | 3 | 5 | 6 | 3 | -1 | -2 |
Уточнить производную в центральных узлах i=2,3.
Порядок выполнения работы.
1.Для аппроксимации производной в узлах i=1,2,3 применяем формулу центральных разностей второго порядка точности с шагом h=0.1:
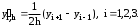
Для аппроксимации производной в узлах i=0 и i=5 применяем формулы для крайних узлов таблицы:
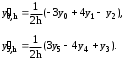
2.Оцениваем величину hопт. С учетом, что
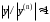 и =10-10 имеем hопт 10-3. Согласно таблицы h > hопт, поэтому для уточнения значений производной в узлах 2 и 3, можно применять метод Рунге-Ромберга.
и =10-10 имеем hопт 10-3. Согласно таблицы h > hопт, поэтому для уточнения значений производной в узлах 2 и 3, можно применять метод Рунге-Ромберга.3.Положим p=2, т.к. при p>2 мы выйдем за пределы таблицы. Для p=2 определяем шаг: h1=2h. Для узлов i=2,3 формула запишется в виде:
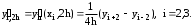
Так как формула второго порядка точности, то k=2. Подставляем и получаем окончательную формулу:
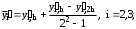
где yi,h- уточненное значение производной.
4.Заполняем таблицу
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| xi | | | | | | |
| yi | | | | | | |
2. Контрольные вопросы
1.Дайте определение конечной разности.
2.Что такое правая, левая, центральная разность?
3. Дайте определение узла и сетки.
4. Дайте определение погрешности аппроксимации производной.
5.Что такое порядок точности ( погрешности )?
6. Напишите порядок точности правой, левой и центральной разности.
7.В чем суть метода Рунге-Ромберга.
8. Дайте определение главной части погрешности аппроксимации.
9. Дайте определение конечной разности для функции двух переменных.
3. Практические задания
1.Написать формулу для вычисления с помощью центральных разностей 2-го порядка точности производную от функции, заданной дискретно, из таблицы заданий №1.
Оценить hопт, полагая, что
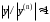 , а =10-10. Улучшить аппроксимацию в заданных узлах с помощью метода Рунге-Ромберга.
, а =10-10. Улучшить аппроксимацию в заданных узлах с помощью метода Рунге-Ромберга.Написать программу и рассчитать на ЭВМ производную этой функции в заданных узлах.
2. Вычислить значение производной функции, заданной в таблице заданий №2 в произвольной точке x=x0 аналитически и численно тремя методами (формулы 2.3, 2.4, 2.5) для пяти значений приращения аргумента Δx=1; 0.2; 0.1; 0.01; 0.001. Результаты расчета вывести на экран и распечатать в виде таблицы:
| Δx | y(x) | y'(x) | | | |
| 1 | | | | | |
| 0.2 | | | | | |
| 0.1 | | | | | |
| 0.01 | | | | | |
| 0.001 | | | | | |
ПРИЛОЖЕНИЕ 5
ВАРИАНТЫ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
В последней колонке число k указывает номер узла, в котором необходимо улучшить точность аппроксимации производной.
Таблица заданий №1
| № | x | Табличные значения f(x) | k | ||||||
| | y | i=0 | i=1 | i=2 | i=3 | i=4 | i=5 | | |
| 1. | x y | 0.01 0.03 | 0.02 0.04 | 0.03 0.03 | 0.04 0.01 | 0.05 0.0 | 0.06 -0.1 | 0 | |
| 2. | x y | 0.1 -0.5 | 0.2 -0.2 | 0.3 0 | 0.4 0.1 | 0.5 0.05 | 0.6 0 | 5 | |
| 3. | x y | 0.05 0.7 | 0.1 0.5 | 0.15 0.7 | 0.2 0.8 | 0.25 0.9 | 0.3 0.12 | 2 | |
| 4. | x y | 0.2 -0.6 | 0.4 -0.5 | 0.6 -0.3 | 0.8 0 | 1.0 0.4 | 1.2 1 | 3 | |
| 5. | x y | 0.1 0.8 | 0.2 0.5 | 0.3 0.4 | 0.4 0.5 | 0.5 0.6 | 0.6 0.9 | 1 | |
| 6. | x y | 0.05 0.0 | 0.1 0.1 | 0.15 0.0 | 0.2 -0.1 | 0.25 -0.2 | 0.3 0.0 | 4 | |
| 7. | x y | 0.01 -0.03 | 0.02 -0.04 | 0.03 -0.03 | 0.04 -0.01 | 0.05 -0.01 | 0.06 -0.1 | 0 | |
| 8. | x y | 0.1 0.3 | 0.2 0.2 | 0.3 0 | 0.4 -0.1 | 0.5 -0.05 | 0.6 0 | 5 | |
| 9. | x y | 0.05 -0.7 | 0.1 -0.5 | 0.15 -0.7 | 0.2 -0.8 | 0.25 -0.9 | 0.3 -0.12 | 2 | |
| 10. | x y | 0.2 0.6 | 0.4 0.5 | 0.6 0.3 | 0.8 0 | 1.0 -0.4 | 1.2 -1 | 3 | |
| 11. | x y | 0.1 -0.8 | 0.2 -0.5 | 0.3 -0.4 | 0.4 -0.5 | 0.5 -0.6 | 0.6 -0.9 | 1 | |
| 12. | x y | 0.05 0.0 | 0.1 -0.1 | 0.15 0.0 | 0.2 0.1 | 0.25 0.2 | 0.3 0 | 4 | |
| 13. | x y | 0.1 0.2 | 0.2 0.3 | 0.3 0.5 | 0.4 0.5 | 0.5 0.2 | 0.6 -0.2 | 2 | |
| 14. | x y | 0.15 -0.2 | 0.25 -0.4 | 0.3 -0.6 | 0.35 -0.5 | 0.4 -0.45 | 0.45 -0.44 | 1 | |
| 15. | x y | 0.5 0.0 | 0.6 1 | 0.7 0.0 | 0.8 -1 | 0.9 0.0 | 1.0 1 | 3 | |
Таблица заданий №2
| Вар. | Вид функции | Вар. | Вид функции |
| 1 | x(t)=Ae-at sin(ωt+b) | 14 | y=ctgm (ax) |
| 2 | x(t)=Aeat cos(ωt+b) | 15 | y(x)=(eax-e-ax)n |
| 3 | | 16 | x(t)=tat |
| 4 | уυ(t)=cos2(at+b) | 17 | y(x)=(ax)sin(bx) |
| 5 | yυ(t)=sin2(at+b) | 18 | |
| 6 | | 19 | |
| 7 | q(t)=(a-btn)n | 20 | |
| 8 | y(x)=xncos(ax) | 21 | R(φ)=arccosm(a+bφn) |
| 9 | | 22 | r(φ)=csin(aφ+b) |
| 10 | | 23 | y(x)=ln(tgn(ax+b)) |
| 11 | | 24 | vυ(t)=loga(tn+bm)k |
| 12 | S(φ)=Вcоsn(aφ+b) | 25 | S(φ)=Asinn(aφ+b) |
| 13 | y=tgax( x/a ) | 26 | X(t)=lg(atn+b) |


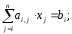
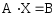 В матричной форме она записывается следующим образом:
В матричной форме она записывается следующим образом: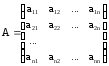
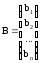
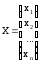 де A - квадратная матрица, В и Х - векторы столбцы вида:
де A - квадратная матрица, В и Х - векторы столбцы вида: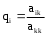
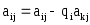
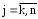 аг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов:
аг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов: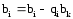
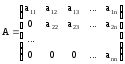
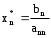 лгоритм обратного хода:
лгоритм обратного хода: 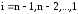
 аг 2. Вычислим:
аг 2. Вычислим: