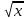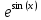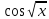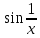Методичка по вычислительной математике. Методы вычислительной математики для решения задач информационно. Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
2.3 Лабораторная работа 3. « Интерполирование функций»Цель: используя интерполяционную формулу, найти значение функции в точке, не являющейся табличной, и оценить погрешность метода решения; подобрать аналитическую формулу, представляющую с некоторой точностью данные табличные значения функции. Порядок выполнения работы Теоретическая часть 1.1 Основные определения Интерполяция - построение кривой, проходящей через контрольные точки.
Постановка задачи интерполяции: поиск такой функции F из заданного класса функций, что Точки xi называют узлами интерполяции, а их совокупность - интерполяционной сеткой. Пары (xi ; yi ) называют точками данных или базовыми точками. Разность между «соседними» значениями Виды интерполяций: 1. Локальная – соединение точек отрезками прямой (по двум точкам), отрезками параболы (по трем точкам). 2. Глобальная – соединение всех точек f(x) единым интерполяционным полиномом. Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел х= xi , где все xi различны, существует единственный многочлен L(x) степени не более n, для которого L(xi) = yi. Получаем непрерывную функцию, проходящую через все точки. Минусы: Требует значительного объема вычислений для нахождения значения функции в произвольной точке. Неопределенное поведение построенной функции между узлами. Будем рассматривать интерполирующие функции, которые задаются отдельно на каждом отрезке, что позволяет лучше учитывать локальное поведение требуемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид). 1.2 Интерполяционные формулы ньютона конечные разностями первого порядка: yi = yi+1 - yi (i = 0, 1, 2, ...). конечные разности второго порядка: 2yi = yi+1 - yi (i = 0, 1, 2, ...) конечные разности третьего порядка: 3yi = 2yi + 1 - 2yi = ( yi + 2 - yi + 1) - ( yi + 1 - yi) = ( yi + 3 - 2yi + 2 + yi + 1) - (yi + 2 - 2yi + 1 + yi ) =yi + 3 - 3yi + 2+ 3yi + 1 - yi таблица конечных разностей:
шаг таблицы: h = хi+1 - xi (i = 0, 1, 2, ..., n) = const; Первая интерполяционная формула Ньютона для интерполирования вперед: 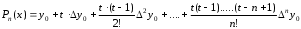 П 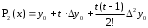 ри n=1 – линейная интерполяция:P1 (x) = у0 + t у0 ри n=1 – линейная интерполяция:P1 (x) = у0 + t у0При n=2 – квадратичная интерполяция: В 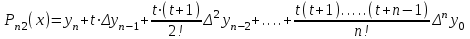 торая интерполяционная формула Ньютона для интерполирования назад: торая интерполяционная формула Ньютона для интерполирования назад: График интерполяционного полинома у = j (х) проходит через заданные точки, т. е., значения полинома j (х) и данной функции у = f (х) совпадают в узлах х = хi (i = 0, 1, .., . n). Если функция f (х) сама является полиномом степени n, то имеет место тождественное равенство f (х) = j (х). В общем случае в точках, отличных от узлов интерполяции R(x) = f (х) - j (х). Эта разность и есть погрешность интерполяции, и называется остаточным членом интерполяционной формулы. О 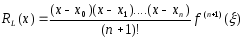 статочный член интерполяционного полинома Лагранжа: статочный член интерполяционного полинома Лагранжа: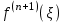 - производная n+1-го порядка. Остаточный член первой интерполяционной формулы Ньютона: 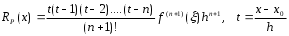 Остаточный член второй интерполяционной формулы Ньютона: 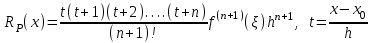 1.3. Экстраполяция Как много значат для современного общества информационные технологии. С трудом можно представить крупные организации, предприятия, фирмы без применения компьютеров, Интернета, программных и аппаратных средств, так упрощающих повседневную, рутинную работу. Между тем работа с информацией, представляющей для ее владельцев ценность, всегда сопровождаются угрозами нарушения ее целостности, расширением доступности, нарушением конфиденциальности. Вследствие реализации этих угроз рядовой пользователь домашнего ПК потеряет не много, в то время как организации, банки, крупные фирмы могут понести серьезный материальный ущерб. Средства защиты информационных систем от злоумышленных воздействий развиваются столь же быстро, как и растет число разнообразных атак на эти системы. Далеко непросто выбрать из столь большого множества способов защиты именно тот, который в нужный момент сможет уберечь ценную информацию от действий «недоброжелателей». Существует масса вариантов как все-таки сберечь «информационные активы» от потерь. Одним из таких способов является прогнозирование вторжений в информационную систему. Прогноз объединяет в себе опыт прошлых лет и материалов для построения стратегии защиты информации в бедующем. Данный материал является основой планирования защиты информации. Процесс прогнозирования может быть выражен в словесной, математической, графической или другой форме. Прогноз позволяет построить возможную модель проведения злоумышленником его атак. Возможность реализации данной модели, а значит и всего прогноза, есть величина вероятностная. На сегодняшний день существует около 150 методов прогнозирования. Любой метод прогнозирования базируется на идее экстраполяции. Под экстраполяцией понимают изучение статистических данных за определенный промежуток времени с последующим выходом за рамки выбранного временного диапазона, с целью формирования прогноза о том или ином изучаемом явлении. Полученные значения позволяют определить связи, закономерности и соотношения, действующие в выбранном временном промежутке. Степень реальности такого рода прогнозов, а значит и мера доверия (к ним) им обусловливаются аргументированностью выбора пределов экстраполяции и стабильностью соответствия "измерителей" по отношению к сущности рассматриваемого явления. Следовательно, функция экстраполяции сводится к выполнению действий, следующих в определённо последовательности: четкое определение задачи и выдвижение гипотез о возможном развитии прогнозируемого объекта; выбор системы параметров, определение единиц измерения, относящихся к каждому параметру; сбор и систематизация данных (обязательно проводится проверка на однородность обрабатываемых данных); выявление данных в ходе экстраполяции тенденции или симптомы изменения изучаемых величин. Эффективность экстраполяции заключается в том, что она позволяет не только составить прогноз, но и своевременно зафиксировать объективно намечающиеся изменения, лежащие в зачатках назревающей тенденции. К основным и наиболее простым методам экстраполяции можно отнести: экстраполяция на основе среднего значения временного ряда (прогнозируемый уровень равен среднему значению уровней в прошлом.); экстраполяция по скользящей и экспоненциальной средней (применяется для краткосрочного прогнозирования). экстраполяция на основе среднего темпа (получение экстраполяции функции в результате использования среднего значения изменения темпа). Следует выделить следующие типы функций экстраполяции: однофакторные прогнозирующие функции; многофакторные прогнозирующие функции. К однофакторным прогнозирующим функциям относят функции, в которых прогнозируемый показатель зависит только от одного факториального признака. Зачастую в качестве факториального признака принимают время. В качестве фактора-аргумента в однофакторной прогнозирующей функции можно использовать не только время, но и другие факторы, если известна их количественная оценка на перспективу. Общий вид формулы не всегда известен, следовательно, вид эмпирической формулы может быть произвольным. Предпочтение отдается обычно наиболее простым формулам, обладающим достаточной точностью. Но каждый прогнозируемый доказательству t (t=1,2…,n)можно рассматривать как функцию от нескольких параметров: в виде линейной многофакторной модели; в виде нелинейной многофакторной модели (степенного типа), которая путем логарифмирования преобразуется в линейную. Более сложные виды нелинейных многофакторных моделей редко используются в практике прогнозирования и планирования. Коэффициенты в моделях определяются с помощью метода наименьших квадратов из системы нормальных уравнений, представляющих собой частные производные равные нулю. 1.4.Метод наименьших квадратов Пусть для исходных данных xi, fi, i=1,…,N, выбран вид эмпирической зависимости: с неизвестными коэффициентами . Запишем сумму квадратов отклонений между вычисленными по эмпирической формуле и заданными опытными данными: 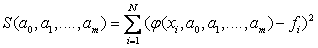 Параметры будем находить из условия минимума функции . Известно, что в точке минимума все частные производные от по равны нулю: В качестве эмпирической функции рассмотрим полином: Формула для определения суммы квадратов отклонений примет вид: 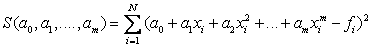 Вычислим производные:  Приравнивая эти выражения к нулю и собирая коэффициенты при неизвестных , получим следующую систему линейных уравнений:  Это нормальная система уравнений. Находим коэффициенты . Если m=1, т.е. , система нормальных уравнений примет вид:  При m=2 имеем:  Как правило, выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих зависимостей и среди них находят наилучшую по минимальной сумме отклонений. 1.5. Прогнозирование Прогнозирование проводилось в два этапа. На первом этапе был спрогнозирована статистика спама на ноябрь и декабрь 2013 года. Затем была рассмотрена статистика вложений вредоносных программ в письма, на основании которой был составлен прогноз вредоносного вложений на ноябрь и декабрь 2013 года. В том и другом случае были задействованы однофакторные функции, а именно: линейная, квадратичная, гиперболическая. По результатам анализа квадратичная зависимость дала более точные результаты. Оптимальное количество факторов-аргументов можно установить с помощью так называемого метода исключений. В качестве примера, иллюстрирующего метод прогнозирования с помощью экстраполяции, можно рассмотреть прогнозирование появления спама в электронных почтовых ящиках пользователей Рунета. Проблема спама как для создателей антивирусов, так и для обычных пользователей стоит довольно остро. Письма с красивой рекламой, заманчивыми предложениями, акциями, в том числе и предложениями о легком «счастье» от мошенников, по большей своей части не только «захламляют» почту пользователя, но и угрожают опасными вредоносными вложениями, которые могут с легкостью нарушить работу системы. Спектр вредоносного вложения богат и может похвастаться разнообразием, которое непрерывно дает пищу для размышлений разработчикам антивирусных программ и систем защиты информации. По результатам статистики за период с мая 2013г. по октябрь 2013г., предоставленной Лабораторией Касперского, были проведены расчеты экстраполяции функции, представленной в виде набора значений, в котором определяющим параметром было выбрано время. 2. Контрольные вопросы Каковы цель и постановка задачи интерполирования? В чем заключается и как решается задача интерполирования? Как построить интерполяционный многочлен по 1-й формуле Ньютона? Как построить интерполяционный многочлен по 2-й формуле Ньютона? Как определяется остаточный член? 3. Практические задания Составить таблицу значений функции, приведенной в приложении 3, разбив заданный интервал на 10 отрезков с h=const. Составить таблицу конечных разностей. По первой и второй интерполяционным формулам Ньютона определить значение функции в точках х = х0±0.25h; х = х0 ±0.5h; х = xl0 ±0.25h; х = xl0 ±0.5h; Построить эмпирическую формулу для заданной функции. Выполнить программную реализацию построения таблицы конечных разностей и эмпирической формулы, а так же расчет значений функций в точках из п. 3. Основные расчетные формулы свести в таблицу:
Результаты вычислений свести в таблицу вида :
ПРИЛОЖЕНИЕ 3 ВАРИАНТЫ ДЛЯ ВЫПОЛНЕНИЯ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
|

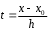 ..
.. 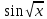
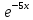
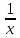 )
)