Методичка по вычислительной математике. Методы вычислительной математики для решения задач информационно. Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
2.6 Лабораторная работа 6. «Методы численного интегрирования функций»Цель: ознакомление с методами численного интегрирования, с понятием порядка точности численного метода, а также со способами контроля численных результатов. Порядок выполнения работы Теоретическая часть Основные определения Рассмотрим вопрос о применении некоторых классов квадратурных формул к вычислению интегралов вида: 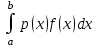 где 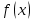 - вещественная функция некоторого класса, заданная на любом конечном или бесконечном отрезке числовой оси - вещественная функция некоторого класса, заданная на любом конечном или бесконечном отрезке числовой оси 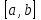 ; ; 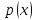 - некоторая фиксированная функция, которую называют весовой. - некоторая фиксированная функция, которую называют весовой.Довольно часто приближенное значение данного интеграла ищут в виде линейной комбинации значений функции 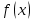 на отрезке на отрезке 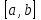 : :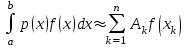 Это приближенное равенство называют квадратурной формулой, определяемой узлами 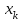 и коэффициентами и коэффициентами 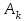 . .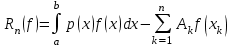 - называют остаточным членом, или остатком квадратурной формулы. Квадратурные формулы с равностоящими узлами применяются для вычисления интеграла: 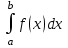 с постоянной весовой функцией и конечным отрезком интегрирования. 1.1.1. Квадратурная формула прямоугольников Пусть на отрезке 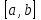 задана функция задана функция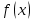 . Введем сетку, разбивающую отрезок . Введем сетку, разбивающую отрезок 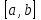 на N равностоящих узлов. на N равностоящих узлов.где 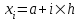 , шаг , шаг 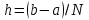 и обозначим и обозначим 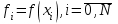 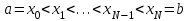 Выберем на каждом сегменте серединную точку 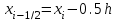 и обозначим и обозначим 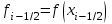 Квадратурная формула прямоугольников имеет вид: 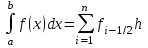 Если функции 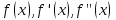 непрерывны на отрезке непрерывны на отрезке 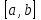 , то остаточный член имеет вид: , то остаточный член имеет вид: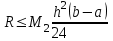 , где , где 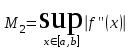 1.1.2. Квадратурная формула трапеций имеет вид: 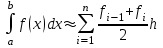 или 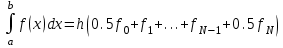 Если функции 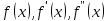 непрерывны на непрерывны на 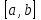 , то остаточный член представляется в виде: , то остаточный член представляется в виде: 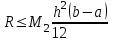 , где , где 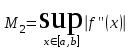 1.1.3. Квадратурная формула Симпсона Выберем на каждом сегменте серединную точку 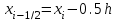 и обозначим и обозначим 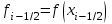 Квадратурная формула Симпсона: 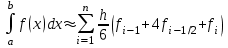 Также можно взять удвоенный частичный отрезок, обозначив 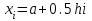 , , 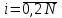 и и 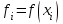 . .В результате получим другой вариант формулы Симпсона: 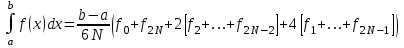 При этом, если функция 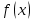 имеет на отрезке имеет на отрезке 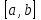 непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид: непрерывные производные до четвертого порядка включительно, то остаточный член имеет вид: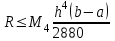 , где , где 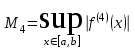 Решая неравенство 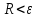 относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность относительно h для остаточных членов любой из квадратурных формул и делая вычисления с таким шагом, получаем заданную точность 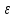 вычисления. вычисления.Контрольный пример Пример 1. Вычислить интеграл 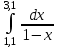 по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы. по квадратурным формулам прямоугольников, трапеций и Симпсона, сравнить с точным значением интеграла и вычислить остаточный член для каждой формулы.Решение: точное значение интеграла: 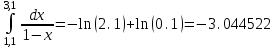 Квадратурная формула прямоугольников Для вычисления интеграла введем сетку, разделяющую отрезок 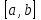 на n=10 частей, при этом h=0,2. Выберем на каждом сегменте на n=10 частей, при этом h=0,2. Выберем на каждом сегменте 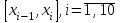 срединную точку срединную точку 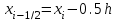 Применяя квадратурную формулу прямоугольников получаем: 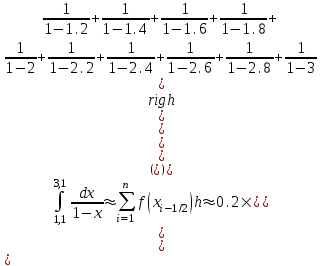 Оценим погрешность по общей формуле. Поскольку 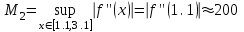 , , то 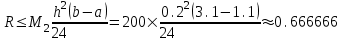 При сравнении точного значения интеграла и полученного имеем разницу 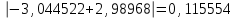 . Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена. . Сравнивая эту разницу с погрешностью, можно сказать, что оценка явно завышена.Квадратурная формула трапеций. Введем сетку также, как в пункте 1. При этом h=0.2, N=10 по квадратурной формуле трапеции: 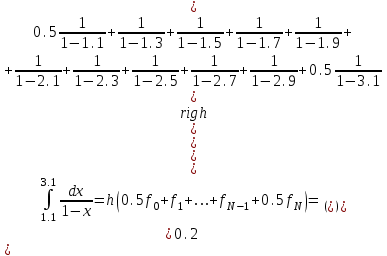 При этом оценка погрешности составляет: 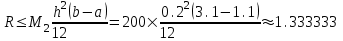 При сравнении точного и полученного значения интеграла разность 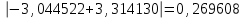 значительно меньше погрешности 0,66666 , что говорит о явно завышенной оценке. значительно меньше погрешности 0,66666 , что говорит о явно завышенной оценке.Квадратурная формула Симпсона. Введем сетку как в пункте 1. Пусть h=0.2, n=10. Чтобы не использовать дробные индексы, обозначим 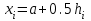 , , 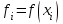 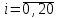 и записываем формулу Симпсона в виде: и записываем формулу Симпсона в виде: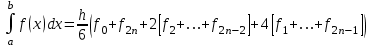 Вычислим интеграл по квадратурной формуле Симпсона: 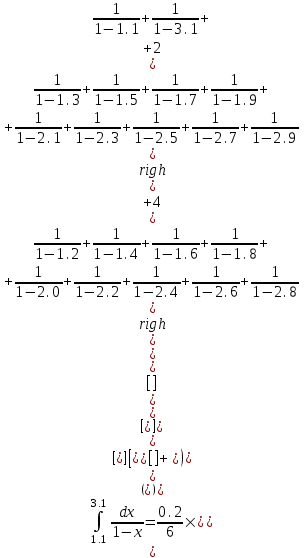 Оценка погрешности этой формулы: 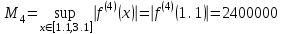 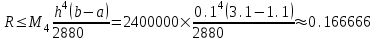 Сравнение точного значения интеграла с полученным дает разность 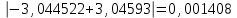 . Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена. . Эта разность меньше погрешности. Можно сказать, что в данном случае оценка также завышена.Пример 2. Выбрать шаг интегрирования для вычисления интеграла 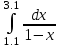 с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона. Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно. с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона. Оценку погрешности для каждой квадратурной формулы будем брать из примера 1 соответственно.1. Квадратурная формула прямоугольников. Вычислим, при каком шаге h погрешность будет составлять 0,01: 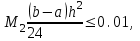 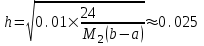 При шаге 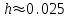 отрезок отрезок 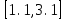 разбивается на N=80 равностоящих узлов. разбивается на N=80 равностоящих узлов.2. Квадратурная формула трапеций. Вычислим, при каком шаге h погрешность составит 0,01: 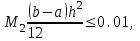 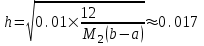 При шаге 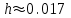 ,отрезок ,отрезок 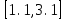 разбивается на N=118 равностоящих узлов. разбивается на N=118 равностоящих узлов.3. Квадратурная формула Симпсона. Вычислим, при каком шаге h погрешность составит 0,01: 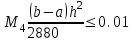 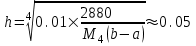 При шаге 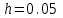 , отрезок , отрезок 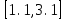 разбивается на N=40 равностоящих узлов. разбивается на N=40 равностоящих узлов.Как и следовало ожидать, наименьшее количество равностоящих узлов N=40 получается при вычислении интеграла по квадратурной формуле Симпсона. 4. Апостериорная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования. Пусть 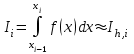 - квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть - квадратурная формула, примененная на частичном отрезке и имеющая порядок m, то есть 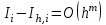 . Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке . Для формул прямоугольников и трапеций m = 3, а для формулы Симпсона m = 5. Проведем на каждом частичном отрезке 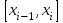 все вычисления дважды, один раз с шагом все вычисления дважды, один раз с шагом 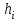 , другой раз с шагом , другой раз с шагом 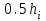 . Тогда справедлива оценка: . Тогда справедлива оценка: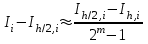 Если для заданного 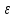 правая часть не превосходит правая часть не превосходит 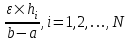 , то получим: , то получим: 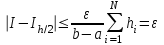 ,то есть будет достигнута заданная точность ,то есть будет достигнута заданная точность 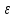 . .Если же на каком-то из частичных отрезков эта оценка не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Заметим, что для некоторых функций такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений, а также возможность увеличения 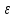 . .2. Контрольные вопросы Какая формула называется квадратурной и почему? Запишите остаток квадратурной формулы. В каком случае применяются квадратурные формулы с равностоящими узлами? Запишите и поясните квадратурную формулу прямоугольников. Запишите и поясните квадратурную формулу трапеций. Запишите и поясните квадратурную формулу Симпсона. Как получается заданная точность вычисления? 3. Практические задания Вычислить приближенное значение интеграла с помощью формулы а) прямоугольников, б) трапеций, в) Симпсона. Величину шага выбрать заранее, сделав вручную оценку погрешности через вторую (случаи а,б) или четвертую (случай в) производные. Сравнить с точным значением интеграла. ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 6. 1.(а) 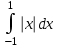 1.(б) 1.(б) 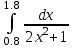 1.(в) 1.(в) 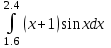 2.(а) 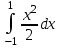 2.(б) 2.(б) 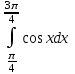 2.(в) 2.(в) 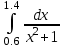 3.(а) 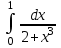 3.(б) 3.(б) 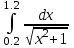 3.(в) 3.(в) 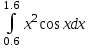 4.(а) 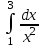 4.(б) 4.(б) 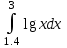 4.(в) 4.(в) 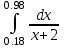 5.(а) 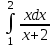 5.(б) 5.(б) 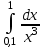 5.(в) 5.(в) 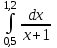 6.(а) 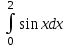 6.(б) 6.(б) 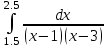 6.(в) 6.(в) 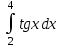 7.(а) 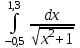 7.(б) 7.(б) 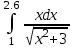 7.(в) 7.(в) 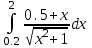 8.(а) 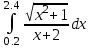 8.(б) 8.(б) 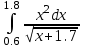 8.(в) 8.(в) 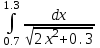 9.(а) 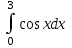 9.(б) 9.(б) 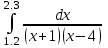 9.(в) 9.(в) 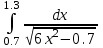 2.7 Лабораторная работа 7. «Метод Рунге-Кутта для системы дифференциальных уравнений». Цель: ознакомление с методами численного решения системы дифференциальных уравнений. Порядок выполнения работы Теоретическая часть Основные определения Уравнения, содержащие производные функции, возникают во многих областях прикладной математики. Вообще говоря, любая физическая ситуация, где рассматривается степень изменения одной переменной по отношению к другой переменной, описывается дифференциальным уравнением. Существует множество приемов для нахождения решений дифференциальных уравнений через элементарные и специальные функции. Но тем не менее очень часто в практических задачах такие методы или вообще не применимы, или приводят к таким сложным решениям, что затраты труда на их получение огромны. Поэтому мы вынуждены обратиться к методам решения, которые могут пригодиться тогда, когда классические методы не срабатывают. Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка или к системе уравнений любого порядка. Но известно, что обыкновенное уравнение N-го порядка можно свести к эквивалентной системе N уравнений первого порядка. Поэтому рассмотрим систему N уравнений первого порядка:  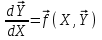 , ,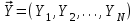 , , 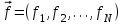 . . Система уравнений (1) имеет множество решений, которое в общем случае зависит от N параметров  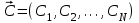 и может быть записано в форме и может быть записано в форме 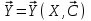 . Для определения значений этих параметров, т.е. для выделения нужного решения, надо наложить . Для определения значений этих параметров, т.е. для выделения нужного решения, надо наложить N дополнительных условий на функции N дополнительных условий на функции  . . Различают три основных типа задач для обыкновенных дифференциальных уравнений: задачи Коши, краевые задачи, задачи на собственные значения. Задача Коши (задача с начальными условиями) имеет дополнительные условия вида:  , ,  , ,т.е. заданы значения всех функций в одной и той же точке. Решение при этом требуется найти на некотором отрезке  (или (или 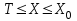 ). ).Следует отметить, что если правые части уравнения (1) непрерывны и ограничены в некоторой окрестности начальной точки 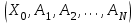 , то задача Коши имеет решение, но, вообще говоря, не единственное. Если правые части не только непрерывны, но и удовлетворяют условию Липшица по переменным , то задача Коши имеет решение, но, вообще говоря, не единственное. Если правые части не только непрерывны, но и удовлетворяют условию Липшица по переменным 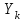 , то решение задачи Коши единственно и непрерывно зависит от координат начальной точки, т.е. задача корректно поставлена. , то решение задачи Коши единственно и непрерывно зависит от координат начальной точки, т.е. задача корректно поставлена.Классы уравнений, для которых разработаны аналитические методы получения точных решений, сравнительно узки и охватывают только малую часть возникающих на практике задач. Например, решение несложного уравнения 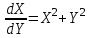 не выражается через элементарные функции. А уравнение 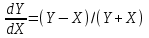 можно точно проинтегрировать и найти общее решение 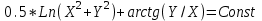 . .Однако для того, чтобы составить таблицу значений 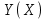 , надо численно решить трансцендентное уравнение, что ничуть не проще численного интегрирования уравнения. , надо численно решить трансцендентное уравнение, что ничуть не проще численного интегрирования уравнения.Численные методы решения дифференциального уравнения – это алгоритмы вычисления приближенных значений искомого решения 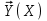 на некоторой выбранной сетке аргумента на некоторой выбранной сетке аргумента 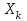 . Решение при этом получается в виде таблицы. Численные методы не позволяют найти общего решения уравнения. Они дают какое-то частное решение. Это основной недостаток численных методов. Зато эти методы применимы к очень широким классам уравнений и всем типам задач для них. . Решение при этом получается в виде таблицы. Численные методы не позволяют найти общего решения уравнения. Они дают какое-то частное решение. Это основной недостаток численных методов. Зато эти методы применимы к очень широким классам уравнений и всем типам задач для них.В основном существуют два широких класса численных методов решения: одноступенчатые и многоступенчатые методы. Одноступенчатые методы используют информацию об искомом решении в одной точке и не производят итераций. К методам этого класса принадлежит и метод Рунге-Кутта. Эти методы являются прямыми (без итераций), что, казалось бы, должно привести к экономии машинного времени, но в действительности эти методы требуют многократных повторных вычислений функции 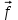 . Кроме того, эти методы имеют тот недостаток, что при их использовании трудно оценивать допускаемую ошибку. . Кроме того, эти методы имеют тот недостаток, что при их использовании трудно оценивать допускаемую ошибку.Многоступенчатые методы позволяют получить решение дифференциального уравнения в следующей точке, но не производя так много вычислений функции 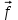 , как при использовании одноступенчатых методов. Здесь для достижения достаточной точности требуются итерации. Большинство методов этого класса называются методами прогноза и коррекции. Хотя и имеются некоторые трудности, связанные с использованием итерационной процедуры и с получением нескольких начальных точек решения , как при использовании одноступенчатых методов. Здесь для достижения достаточной точности требуются итерации. Большинство методов этого класса называются методами прогноза и коррекции. Хотя и имеются некоторые трудности, связанные с использованием итерационной процедуры и с получением нескольких начальных точек решения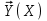 , но они уравновешиваются тем фактом, что оценку ошибки при использовании этого метода легко получить в качестве побочного продукта вычислений. , но они уравновешиваются тем фактом, что оценку ошибки при использовании этого метода легко получить в качестве побочного продукта вычислений. Численные методы можно применять только к конкретно поставленным задачам. Нужно чтобы малые изменения начальных условий приводили бы к достаточно малому изменению интегральных кривых. Если это условие не выполняется, то небольшие изменения начальных условий или эквивалентные этим изменениям небольшие погрешности численного метода могут сильно исказить решение. Рассмотрим теперь, как решается методом Рунге-Кутта задача Коши. Построим семейство схем второго порядка точности и на его примере разберем основные идеи метода. Выберем на отрезке 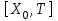 некоторую сетку: некоторую сетку: 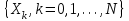 значений аргумента так, чтобы выполнялись соотношения значений аргумента так, чтобы выполнялись соотношения 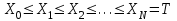 (сетка может быть неоднородной). Разлагая решение системы уравнений (2) (сетка может быть неоднородной). Разлагая решение системы уравнений (2) 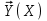 в ряд Тейлора на интервале сетки в ряд Тейлора на интервале сетки 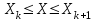 , получим: , получим: 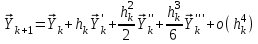 Здесь введены обозначения: 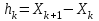 , , 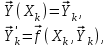 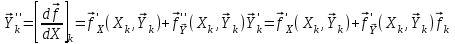 . .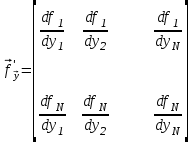 Чтобы избежать дифференцирования функции 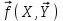 ,заменим производную ,заменим производную 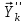 разностью: разностью: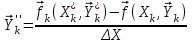 , ,соответственно выбирая 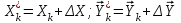 . .После такой замены, объединяя одинаковые члены, приближенное решение 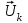 (отбрасываем члены третьего порядка и выше по шагу) можно записать в виде: (отбрасываем члены третьего порядка и выше по шагу) можно записать в виде: 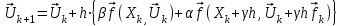 Для простоты в формуле полагалось, что сетка является равномерной с шагом h. Здесь 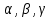 --- параметры, значения которых выбираем таким образом, чтобы минимизировать ошибку метода Рунге---Кутта на каждом шаге --- параметры, значения которых выбираем таким образом, чтобы минимизировать ошибку метода Рунге---Кутта на каждом шаге 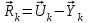 . Рассматривая правую часть соотношения как функцию от h, разложим ее в ряд по степеням шага в окрестности точки . Рассматривая правую часть соотношения как функцию от h, разложим ее в ряд по степеням шага в окрестности точки 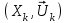 : :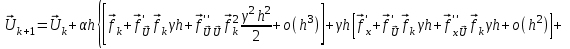 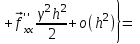 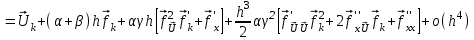 . .С другой стороны, для точного решения дифференциального уравнения 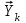 имеем: имеем: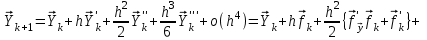 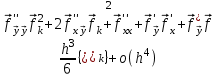 . .Оценим погрешность приближенного решения, полученного методом Рунге-Кутта второго порядка точности на одном шаге. 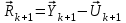 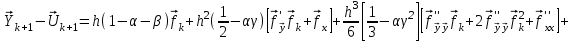 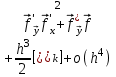 Чтобы получить схему Рунге-Кутта 2-го порядка точности, необходимо обнулить коэффициенты в 1-ом и 2-ом членах соотношения: 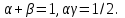 Выражая через 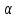 остальные параметры и подставляя их, получим однопараметрическое семейство схем Рунге-Кутта 2-го порядка точности: остальные параметры и подставляя их, получим однопараметрическое семейство схем Рунге-Кутта 2-го порядка точности: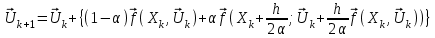 , где , где 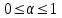 Формула имеет неплохую точность и нередко используется в численных расчетах. При этом обычно полагают либо 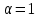 , либо , либо 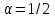 . Эти два случая часто называют улучшенными (модифицированными) методами Эйлера. . Эти два случая часто называют улучшенными (модифицированными) методами Эйлера. Методом Рунге-Кутта можно строить схемы различного порядка точности. Например, схема ломаных (метод Эйлера) есть схема Рунге-Кутта первого порядка точности. Наиболее употребительными в вычислительной практике являются схемы четвертого порядка точности. Приведем без вывода одну из них, которая записана в большинстве стандартных программ ЭВМ: 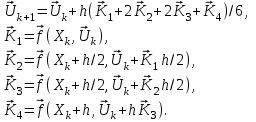 Схемы Рунге-Кутта имеют ряд важных достоинств: все схемы допускают расчет с переменным шагом, нетрудно уменьшить шаг там, где функция быстро меняется, и увеличить его в обратном случае; для начала расчета достаточно выбрать сетку 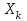 и задать значение и задать значение 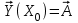 ; далее вычисления идут по одним и тем же формулам. Шаг сетки следует выбирать настолько малым, чтобы обеспечить требуемую точность расчета. Других ограничений на шаг в методе Рунге-Кутта нет. ; далее вычисления идут по одним и тем же формулам. Шаг сетки следует выбирать настолько малым, чтобы обеспечить требуемую точность расчета. Других ограничений на шаг в методе Рунге-Кутта нет.Встречаются задачи, в которых функции являются достаточно гладкими, но настолько быстро меняющимися, что схема Рунге-Кутта как низкого, так и высокого порядка точности требуют неприемлемо малого шага для получения удовлетворительного результата. Такие задачи требуют использования специальных методов, ориентированных на данный узкий класс задач. 2. Контрольные вопросы Как описываются обыкновенные дифференциальные уравнения? Перечислите основные типа задач для обыкновенных дифференциальных уравнений. Опишите задачу Коши. Что из себя представляют численные методы решения дифференциального уравнения? Опишите классы численных методов решения дифференциального уравнения Опишите алгоритм метода Рунге-Кутта задача Коши. Как оценивается погрешность приближенного решения обыкновенного дифференциального уравнения, полученного методом Рунге-Кутта второго порядка точности на одном шаге? Назовите достоинства схемы Рунге-Кутта. 3. Практические задания Методом Рунге-Кутта (2-го или 4-го порядка точности) найдите решение системы дифференциальных уравнений на отрезке 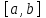 при начальных условиях с шагом при начальных условиях с шагом 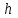 . Шаг выбрать самостоятельно. Численные решения . Шаг выбрать самостоятельно. Численные решения 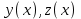 представьте графически. Сравните с аналитическим решением, если его можно найти. представьте графически. Сравните с аналитическим решением, если его можно найти.ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 7. 1. 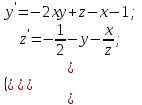 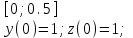 2. 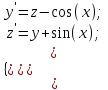 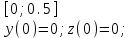 3. 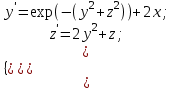 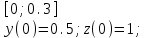 4. 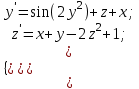 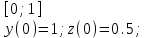 5. 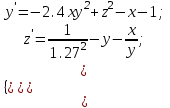 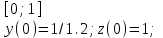 6. 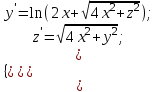 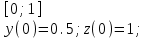 7. 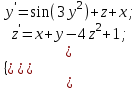 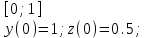 8. 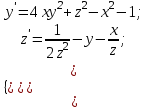 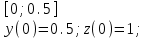 9. 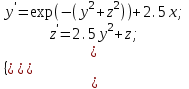 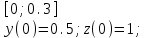 10. 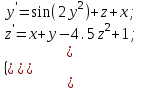 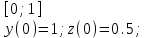 11. 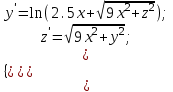 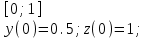 12. 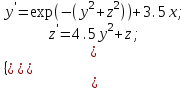 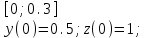 13. 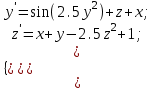 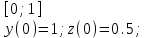 14. 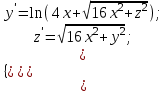 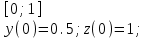 Рекомендуемая литератураЗенков А.В.. Численные методы: учеб. пособие для прикладного бакалавриата.- М.: Изд-во Юрайт, 2019.- 122с.- ISBN 978-5-534-10893-4 Пирумов У.Г. Численные методы: учебник и практикум для академического бакалавриата. - М.: Изд-во Юрайт, 2019.- 421с.-ISBN 978-5-534-03141-6 Пименов В.Г. Численные методы. В 2 ч.: учеб. пособие для вузов - М.: Изд-во Юрайт, 2019; Екатеринбург: Изд-во Урал. ун-та.-111 с. и 106с.- ISBN 978-5-534-10886-6(Ч.1); ISBN 978-5-534-10891-0(Ч.2). Зализняк В.Е. Численные методы. Основы научных вычислений: учебник и практикум для академического бакалавриата. - М.: Изд-во Юрайт, 2019.- 356с.- ISBN 978-5-534-02714-3 Гателюк О.В. Численные методы: учеб. пособие для академического бакалавриата.- М.: Изд-во Юрайт, 2019.- 140с.- ISBN 978-5-534-05894-9 Абрамкин Г.П. Численные методы: учеб. пособие - Изд-во Алтайского гос.пед. ун-та, 2016.-260с.- ISBN 978-5-88210-829-7 Семакин, И.Г. Программирование, численные методы и математическое моделирование: учебное пособие / Семакин И.Г., Русакова О.Л., Тарунин Е.Л., Шкарапута А.П. — Москва : КноРус, 2017. — 298 с. — (для бакалавров). — ISBN 978-5-406-00862-1. |
