Начальный курс топологии. Учебнометодическое пособие Редактор И. Н. Никитина

• Название: Учебнометодическое пособие Редактор И. Н. Никитина
• Анкор: Начальный курс топологии
• Дата: 31.01.2022
• Размер: 4 Mb.
• Имя файла: Начальный курс топологии.doc
• Тип: Учебно-методическое пособие; #347044
• страница: 8 из 8

Задание 5. Найти эйлерову характеристику двумерного многообразия , построив конкретное клеточное разбиение, и эйлерову характеристику двумерного многообразия , пользуясь теоремой о «склеивании» двумерных многообразий, если - сфера, - сфера с двумя «дырками», заклеенными двумя «ручками».

Решение.

Изобразим сферу и предложим ее следующее клеточное разбиение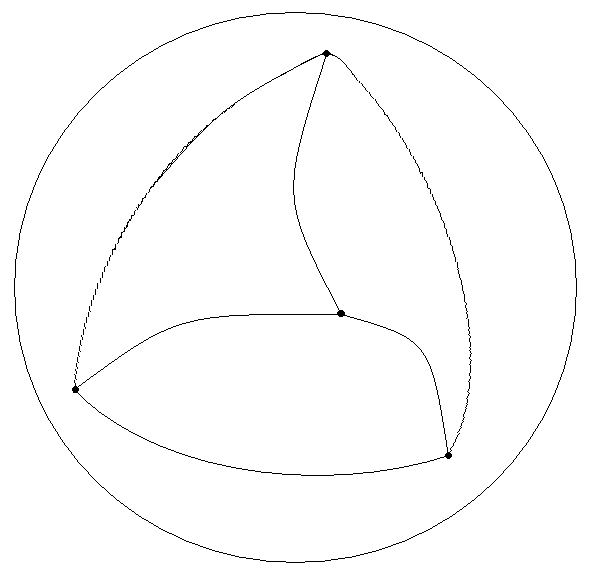



Тогда , , , где - число вершин, - число сторон, - число клеток.

Эйлерова характеристика вычисляется по формуле: . В нашем случае .

Так как двумерное многообразие получено «склеиванием» сферы с двумя «дырами» и двух «ручек» и , то по теореме о «склеивании» двумерных многообразий имеем:
. (1)
Эйлерова характеристика сферы с «дырами» вычисляется по формуле . В нашем случае , поэтому

. (2)

Как известно, эйлерова характеристика «ручки» равна - 1, поэтому
. (3)

Тогда в силу равенств (1), (2), (3) имеем:
.
ТЕСТ по курсу «геометрия-топология»

2 семестр, отд. МоАИС
А 1. Декартовым произведением двух непустых множеств А и В называется

1. множество всех упорядоченных пар (х, у), где х, у  АВ

2. множество всех упорядоченных пар (х, у), где х, у  АВ

3. множество всех упорядоченных пар (х, у), где х  А, у  В

4. множество пар (х, у), где х  А, у  В

5. другое определение

А 2. Пусть заданы прямоугольник  и отрезок [A, B]. Что задает декартово произведение: [A, B]?

1. плоскость 2. параллелепипед 3. цилиндрическую поверхность 4. сферу 5. шар.

А 3. Метрикой  пространства Х называется

1. отображение : Х  Х  R, удовлетворяющее следующим аксиомам: а)  х, у  Х |  (х, у)  0 в)  х, у  Х |  (х, у) =  (у, х)

с)  х, у, z  Х |  (х, у) +  (у, z)   (х, z)

2. отображение : Х  Х  R, удовлетворяющее следующим аксиомам: а)  х, у  Х |  (х, у)  0, причем  (х, у) = 0  х = у

в)  х, у, z  Х |  (х, у) +  (у, z)   (х, z)

3. отображение : Х  Х  R, удовлетворяющее следующим аксиомам: а)  х, у  Х |  (х, у)  0, причем  (х, у) = 0  х = у

в)  х, у  Х |  (х, у) =  (у, х)

4. отображение : Х  Х  R, удовлетворяющее следующим аксиомам:

а). х, у  Х |  (х, у)  0, причем  (х, у) = 0  х = у

в).  х, у  Х |  (х, у) =  (у, х)

с).  х, у, z  Х |  (х, у) +  (у, z)   (х, z)

5. другое определение

А 4. Указать, какая функция (х, у) , заданная на числовой прямой R, является метрикой на R

1. (х, у) = х – у 2. (х, у) = (х – у)² 3. (х, у) =| х – у|

4. (х, у) = х² – у² 5. (х, у) = | 2х – у|

А 5. Семейство Ф называется топологией или топологической структурой заданной на непустом множестве Х, если

1. а) само множество Х и пустое множество  принадлежат Ф

в) объединение любых двух множеств из Ф также принадлежит Ф

с) пересечение любого семейства множеств из Ф также принадлежит Ф

2. а) само множество Х и пустое множество  принадлежат Ф

в) объединение любого конечного числа множеств из Ф также принадлежит Ф

с) пересечение любых двух множеств из Ф также принадлежит Ф

3. а) само множество Х и пустое множество  принадлежат Ф

в) объединение любого семейства множеств из Ф также принадлежит Ф

с) пересечение любого семейства множеств из Ф также принадлежит Ф

4. а) само множество Х и пустое множество  принадлежат Ф

в) объединение любого семейства множеств из Ф также принадлежит Ф

с) пересечение любых двух множеств из Ф также принадлежит Ф

5. другое определение

А 6. Множество G топологического пространства (Х, Ф). называется открытым множеством, если

1. G – подмножество Х 2. G – подпространство топологического пространства (Х, Ф) 3. G – элемент множества Ф 4. G – непустое множество 5. другое определение

А 7. Множество Н топологического пространства (Х, Ф) называется замкнутым множеством, если

1. Н – подмножество Х 2. Н – подпространство топологического пространства (Х, Ф) 3. Н – элемент множества Ф 4. Н – непустое множество 5. Н = С _ХG, где G – элемент множества Ф

А 8. Пусть Х . Будет ли Ф = {G_}, где G_ – подмножества из Х, топологией?

1. Ф = { , одна точка х  Х} 2. Ф = { , X, две точки х, у  Х}

3. Ф = { , X, две точки х, у  Х, пара (х,у)} 4. Ф = { любое подмножество Х} 5. Ф = { , Х, одна точка х  Х}

А 9. Точка х называется внешней точкой множества H в топологическом пространстве (Х, Ф),

1. если любая окрестность точки х содержится в H

2. если существует такая окрестность V точки х, в которой нет точек из H, то есть V  С_х H = Х \ H

3. если в любой окрестности точки х имеются как точки множества H так и точки не принадлежащие H

4. если существует такая окрестность U точки х, что U  H

5. если любая окрестность точки х содержится в С_Х H

А 10. Точка х называется граничной точкой множества H в топологическом пространстве (Х, Ф),

1. если любая окрестность точки х содержится в H

2. если существует такая окрестность V точки х, в которой нет точек из H, то есть V  С_х H = Х \ H

3. если в любой окрестности точки х имеются как точки множества H, так и точки не принадлежащие H

4. если существует такая окрестность U точки х, что U  H

5. если любая окрестность точки х содержится в С_Х H

А 11. Множество всех внешних точек множества H обозначается

1. int H 2. ext H 3.  H 4. 5. С_Х H

А 12. Точка называется точкой прикосновения множества H, если

1. существует окрестность U точки , такая, что U  H =  

2. в каждой окрестности точки  H существуют точки множества H, отличные от

3. каждая окрестность точки имеет с H хотя бы одну общую точку

4. существует окрестность точки , которая имеет с H хотя бы одну общую точку

5. другое определение

А 13 Если замкнутое множество F содержит множество H, то

1. F содержит ext 2. F содержит предельные точки множества Н

3. F содержит intС_Х Н 4. F содержит 5. F содержит С_х(C_x H)

А 14. Какие равенства справедливы?

1. Int H  ext H  H=  2. Int H  H = Int H  ext H

3. ext H Int С_Х H =  4. Int H  H = ext H 5. Int H ext H  H= Х

А 15. Какие из данных множеств топологического пространства (Х, Ф) являются открытыми (Н  Х)?

1. Int H  ext H 2. Int H \ H 3. H 4. Int H  H 5. .

А 16. Топологическое пространство (Х, Ф) называется Хаусдорфовым, если:

1. сходящаяся последовательность точек х_n имеет единственный предел 2. для любых двух множеств существуют их непересекающиеся окрестности 3. для любых двух различных точек пространства существуют их непересекающиеся окрестности 4. существует семейство U = А_ открытых множеств А_  (Х, Ф) таких, что Х  5. другое определение.

А17. Топологическое пространство (Х, Ф) называется компактным, если

1. существует семейство U = А_ открытых множеств А_  (Х,Ф) таких, что Х 

2. из его открытого покрытия можно выбрать конечное подпокрытие

3. из любого его открытого покрытия можно выбрать конечное подпокрытие

4. другое определение

5. если из любого его конечного покрытия можно выбрать подпокрытие

А 18. Топологическое пространство (Х, Ф) называется несвязным, если

1. его замыкание является связным множеством

2. существуют два непустых открытых множества U и V таких, что

U  V = Х и U  V = 

3. у него нет изолированных точек

4. может быть разбито на два непустых множества, не имеющих между собой общих точек

5. другое определение

А 19. Пусть даны топологические пространства (Х, Ф), (У, W) и отображение : X  У

Отображение : X  У называется непрерывным в точке х₀  Х, если

1. для каждой окрестности U точки х₀ существует такая окрестность V точки (x₀), что (U) . V

2. для каждой окрестности V точки f(x₀) существует такая окрестность U точки х₀, что ^-1(V)  U

3. для каждой окрестности V точки (x₀) существует такая окрестность U точки х₀, что (U)  V

4. : X  У непрерывно в каждой точке пространства Х

5. полный прообраз любого открытого (замкнутого) множества будет открытым (замкнутым) множеством

А 20. Пусть даны топологические пространства (Х, Ф), (У, W) .

Отображение : X  У называется гомеоморфизмом, если

1. – биекция и, при этом, отображения непрерывно

2. – биекция и, при этом, отображение ^--1 – непрерывно

3. – биекция и, при этом, отображения и ^--1 – непрерывны

4. – сюръекция и, при этом, отображения непрерывно

5. другое определение

А 21. Укажите гомеоморфные пары топологических пространств.

1. любые два интервала (а, b) и (c, d), заданные на числовой прямой, с топологией порожденной метрикойы топологических пространств гомеоморфны



2. U = U / 0  U  2 П и S = S (0, 1) – окружность радиуса 1 с центром в начале координат

3. любые два промежутка [а, b) и (c, d], заданные на числовой прямой, с топологией порожденной метрикойы топологических пространств гомеоморфны



4.поверхности куба и тора, заданные в трехмерном пространстве с топологией, порожденной метрикой

5. сфера и поверхность куба, заданные в трехмерном пространстве с топологией, порожденной метрикой

А 22. Вычислить эйлерову характеристику сферы с двумя дырками, заклеенными листами Мебиуса и тремя дырками, заклеенными ручками

1. – 7 2. – 6 3. – 5 4. 5 5. 4

А 23. Укажите неориентируемые двумерные многообразия.

1. сфера с дыркой, заклеенной листом Мёбиуса

2. сфера с дыркой, заклеенной ручкой

3. сфера с тремя дырками, две из которых заклеены листами Мёбиуса, а одна ручкой

4. тор с тремя дырками, две из которых заклеены ручками, а одна листом Мёбиуса

5. сфера с двумя дырками

А 24. На числовой прямой с топологией заданной метрикой имеем подмножество Н = {x| x (– ; –3)xQ}(–3; 2]{3;4;5;}[5; 11).

Найти H

1. (– , – 3]  {2,3,4,5,11} 2. [– 3,2]  {3,4,5,11} 3. (– , – 3]

4. {3,4,5} 5. {– 3, 2}

№	Номера заданий
	1	2	3	4	5	6	7	8	9	10	11	12
Отв.	3	2	4	3	4	3	5	345	2	3	2	3
№	Номера заданий
	13	14	15	16	17	18	19	20	21	22	23	24
Отв.	245	25	12	3	3	2	3	3	15	2	134	1

СПИСОК ЛИТЕРАТУРЫ

1. 
   Александров А.Д., Нецветаев Н.Ю. Геометрия. – М.: Наука, 1990. –672 с.
   
2. 
   Аминов Ю.А. Свойства в целом кривых в трехмерном евклидовом пространстве, связанные с кручением // Укр. геом. сб. – 1973. – Вып. 14. – С. 3 – 10.
   
3. 
   Аминов Ю.А. Дифференциальная геометрия и топология кривых. – М.: Наука, 1987. –160 с.
   
4. 
   Атанасян Л.С., Базылев В.Т. Геометрия. Ч.2. – М.: Просвещение, 1987. – 351 с.
   
5. 
   Беклемишева Л.А. и др. Сборник задач по аналитической геометрии: Учеб. пособие. – М., 2003.
   
6. 
   Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учеб. пособие. – М.: Высшая школа, 2005.
   
7. 
   Вернер А.Л., Кантор Б.Е. Элементы топологии и дифференциаль-
   

ной геометрии. – М.: Просвещение, 1985. – 113 с.

8. 
   Вернер А.Л., Кантор Б.Е., Франгулов С.А. Геометрия.Ч.2. – СПб., 1997.
   
9. 
   Гильберт Д., Кон-Фоссен С. Наглядная геометрия. – М.: Наука, 1981. – 352 с.
   
10. 
    Дубровин Б.А.,Новиков С.П., Фоменко А.Т. Современная геометрия. – М.: Наука, 1986. – 759 с.
    
11. 
    Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. – М., 2004. – 464 с.
    
12. 
    Жаферов А.Ф. Геометрия: В 2 ч. Ч.1. – Новосибирск: Сиб.унив.изд-во, 2002. – 271 с.
    
13. 
    Жаферов А.Ф. Геометрия: В 2 ч. Ч.2. – Новосибирск: Сиб.унив.изд-во, 2003. – 267 с.
    
14. 
    Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии: Учебник для университетов. – М.: Наука, 1987. – 432 с.
    
15. 
    Кон-Фоссен С. Некоторые вопросы дифференциальной геометрии в целом. – М.: Физматгиз, 1959.
    
16. 
    Рохлин В.А., Фукс Д.Б. Начальный курс топологии. М.: Наука, 1977. – 488 с.
    
17. 
    Погорелов А.В. Геометрия. – М.: Наука, 1983. – 288 с.
    

18. Шилов Г.Е. Математический анализ. Функции одного переменного. Ч. – 3. – М.: Наука,1970. – 352 с.

19. Шварц Дж. Дифференциальная геометрия и топология.Новокузнецк: НФМИ, 2000.

20. Шашкин Ю.А. Эйлерова характеристика. М.: Наука,1984. – 96 с.

21. Фоменко А.Т. Дифференциальная геометрия и топология. Дополнительные главы. – М.: Изд-во Моск. ун-та, 1983. – 216 с.

22. Энгелькинг Р. Общая топология. – М.: Мир,1986.