Начальный курс топологии. Учебнометодическое пособие Редактор И. Н. Никитина

• Название: Учебнометодическое пособие Редактор И. Н. Никитина
• Анкор: Начальный курс топологии
• Дата: 31.01.2022
• Размер: 4 Mb.
• Имя файла: Начальный курс топологии.doc
• Тип: Учебно-методическое пособие; #347044
• страница: 2 из 8

§ 3. ПОНЯТИЕ ПОДПРОСТРАНСТВА. ЗАМКНУТЫЕ

МНОЖЕСТВА

ВНУТРЕННИЕ, ВНЕШНИЕ И ГРАНИЧНЫЕ ТОЧКИ
Понятие подпространства

Если У подмножество Х, а (Х, Ф) – топологическое пространство, то на У можно рассматривать топологию
 =   У  G  Ф .
Действительно, обозначим:

S =  У ,  =  S .

1.  , У  .

2. S = (G  У) = ( G ) У  .

3. S  S = (G  У)  (G  У) = (G G )  У  .

(У,  ) – называют топологическим подпространством пространства (Х, Ф), а  - топологией, индуцированной топологией Ф.

Пример 1. Пусть Е₃ – трёхмерное евклидово пространство. Открытый шар U (M₀, r) с центром М₀ и радиусом r > 0 определяем как множество точек М Е₃:

U (M₀, r), = М  | M M₀| < r .
Открытым в Е₃ называется множество G , каждая точка которого является центром открытого шара, целиком лежащего в G.

Пустое множество считается открытым.

В первом параграфе мы показали, что совокупность открытых множеств представляет топологию (обычная топология метрического пространства, то есть порождённая метрикой). Если Е₂ – плоскость в Е₃, то U (M₀, r)  Е₂ = w (M₀, r), то есть открытый круг.

Если Е₁ – прямая в Е₃ (или множество R – действительных чисел), то

U (M₀, r)  Е₁ = (    ) - интервал. Соответственно, в Е₂ и Е₁ получаем открытые множества, которые согласуются с данным выше определением открытого множества в Е₃.

Пример 2. Пусть Х = Е³. Открытыми в Х множествами назовем только открытые шары U(r) с общим центром О и радиусами r , а также все множество Х и пустое множество. Ранее мы доказали, что набор открытых множеств (см. § 2, пример 4 ) задает топологию Ф_к на Х, то есть (Х, Ф_к) топологическое пространство.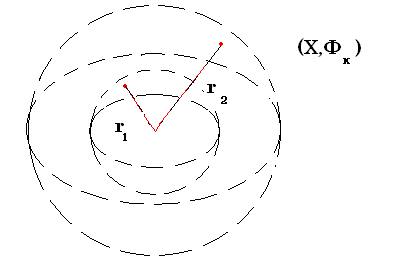



Рассмотрим плоскость, проходящую через точку О и обозначим ее У. Тогда У – подмножество Х и на У индуцируется следующая топология: открытыми множествами будут У,  и открытые круги с общим центром О и радиусами r.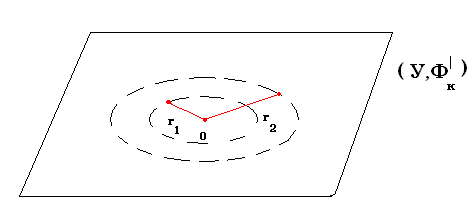


Замкнутые множества

Определение 3. Подмножество А топологического пространства

(Х, Ф) называется замкнутым, если его дополнение Х \ А открытое множество.

Так как дополнение к дополнению множества А есть снова А, то получаем: множество А открыто в том и только в том случае, когда дополнение к нему замкнуто.

Если (Х, Ф) - антидискретное топологическое пространство, то дополнения к Х и к  являются единственными замкнутыми множествами, но учитывая, что

Х / Х =  , Х /  = Х,

получаем:  и Х – являются также и замкнутыми множествами.

Х и  замкнуты (и одновременно открыты) в любом топологическом пространстве (Х, Ф).

Если Ф – дискретная топология, то любое множество замкнуто и открыто.

Если Х – множество действительных чисел и Ф обычная топология, то есть индуцированная естественной метрикой, то множество
  = х   х   = Х \ ((– , )  ( , + ))

замкнуто.

Используя формулы де Моргана

Х \  =  (X \ ),

Х \  =  (X \ ),

несложно доказывается следующая теорема.

Теорема 1. (Свойства замкнутых множеств)

1. Пересечение любой совокупности замкнутых множеств есть замкнутое множество.

2. Объединение любых двух замкнутых множеств есть замкнутое множество.

Доказательство. Пусть для любого  определено множество

F = X \ ,

где - открытое множество в (Х, Ф).

1. 
   F₀ =  F = (X \ ) = X \(  ).
   

Так как  = G₀  , то F₀ – замкнуто.

2. 
   F = F₁  F₂ = (X \ G₁)  (X \ G₂) = X \ (G₁  G₂).
   

Так как G₁  G₂ = G  , то F – замкнуто.
Замечание. Методом математической индукции аксиома 3 топологического пространства и пункт 2) теоремы 1 обобщаются на любое конечное число множеств.

Теорема 2. Пересечение любого конечного числа открытых множеств является открытым множеством; объединение любого конечного числа замкнутых множеств является замкнутым множеством.

Однако, если в R с обычной топологией рассмотреть множества

G_n = ,

то

G_n = –1, 1,

то есть мы указали пример, когда пересечение бесконечного множества открытых множеств оказалось замкнутым.
Внутренние, внешние и граничные точки

Пусть (Х, Ф) – топологическое пространство. Открытое множество U называется окрестностью точки х если х  U (х  X и U  Ф).

Определение 4. Точка называется внутренней точкой некоторого множества H (H  X), если существует такая окрестность U точки ,что U  H. Множество всех внутренних точек множества H обозначается через int H и называется внутренней областью H или внутренностью H.

Определение 5. Точка называется внешней точкой множества H, если существует такая окрестность V точки , в которой нет точек из H, т.е. V  С_х H=Х \ H. Множество всех внешних точек множества H обозначается через ext H и называется внешней областью H.

Определение 6. Точка с называется граничной для множеств H, если в любой окрестности точки с имеются как точки множества H, так и точки не принадлежащие H.

Множество всех граничных точек множества H обозначается через 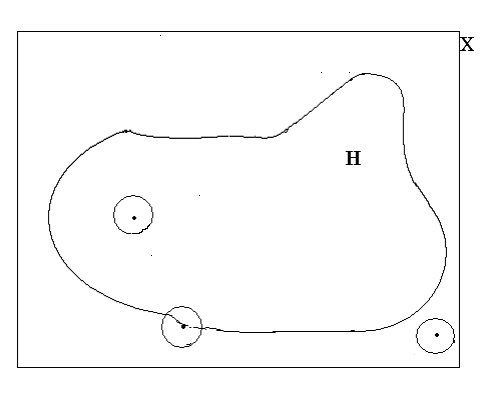H и называется границей H.


Очевидно:

int H  ext H  H = X

int H  ext H = ext H  H = int  H = 

int H = ext C_x H, ext H = int C_x H

H = C_x H

Теорема 3. Для любого множества H топологического пространства (Х, Ф) имеем

int H  Ф ,ext H  Ф.

H – замкнутое множество.

Доказательство. По определению для   int H существует окрестность U_ точки такая, что U_  H.

Поскольку открытое множество является окрестностью любой своей точки, то U_  int H , то есть U_ состоит только из внутренних точек H.

Тогда int H = U_ и в силу аксиомы 2 топологического пространства получим int H  Ф.

Так как ext H = int (X \ H), то получаем ext H  Ф.

Так как H = X \ (int H  ext H ), то H замкнуто в (Х, Ф).

Определение 7. Точка называется точкой прикосновения множества H, если каждая окрестность точки имеет с H хотя бы одну общую точку.

Множество всех точек прикосновения множества H называется замыканием множества H и обозначается . Ясно, что = int H  H и является замкнутым множеством.

Определение 8. Точка  H называется изолированной точкой множества H, если существует окрестность U точки , такая, что

U  H = 

Определение 9. Если  и не является изолированной для H, то она называется предельной точкой множества H.

Ясно, что в каждой окрестности предельной точки  H существуют точки множества H, отличные от .

Поскольку замыкание распадается на множество изолированных и предельных точек, а первое всегда содержится в H, то приходим к следующему утверждению:

Теорема 4. Множество H замкнуто тогда и только тогда, когда оно содержит все свои предельные точки, то есть, если

H =

Действительно, если H – замкнуто, то C H = X \ H открыто. Поэтому C H = ext H.

Отсюда получаем

H = int H  ∂ H = .

Теорема 5. Если замкнутое множество F содержит множество H, то F содержит и .

Доказательство. Так как H  F, то все предельные точки H будут являться предельными и для F, а поэтому они принадлежат F, следовательно

 F.

Следствие. Замыкание множеств H есть пересечение всех замкнутых множеств, содержащих H.

Действительно, согласно теореме 5 принадлежит любому замкнутому множеству, содержащему H , а по теореме 3 из §3 - замкнутое множество.

Пример 1. Если (Х, Ф) – антидискретное топологическое пространство, то внутренность любого его подмножества, за исключением самого Х, пустое множество.

Если (Х, Ф) – дискретное пространство, то любое его подмножество открыто и замкнуто одновременно и, следовательно, совпадает со своей внутренностью и со своим замыканием.

Если X = R с обычной топологией, то внутренность множества всех целых чисел пустое множество.

Внутренность множества рациональных чисел – пустое множество. Поэтому получаем, что замыкание = R, а замыкание внутренности множества рациональных чисел = , при этом int = R.

Таким образом, замыкание внутренности множества может сильно отличаться от внутренности замыкания.

Таким образом, оператор перехода к внутренности и оператор замыкания, вообще говоря, не коммутируют.

Если Х – антидискретно и А  Х, А  , то А = Х.

Если Х – дискретно и А  Х, А  , то А = .

Границей множества рациональных чисел, так же как и границей множества всех иррациональных чисел, служит всё множество вещественных чисел.

Пример 2. Пусть , , Найти и все замкнутые множества.

Решение.

Рассмотрим точку и выберем из списка открытых множеств , такое которое содержит точку и входит в . Очевидно, следовательно, . Для точки такого открытого множества нет. Следовательно, . Точка и поэтому . Итак окончательно получаем .

.

. Найдем .

Рассуждая аналогично, получаем, что 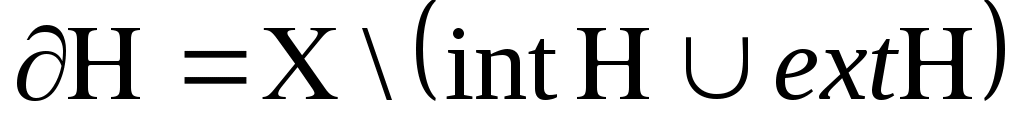. 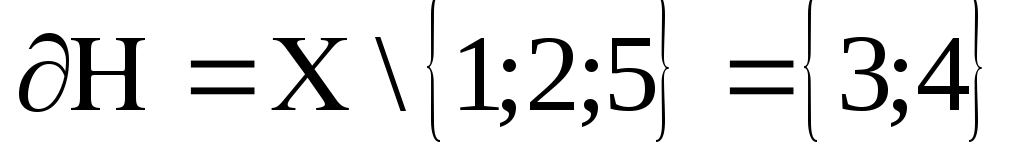Для точки нет открытого множества содержащегося в . Следовательно, , . Для нахождения граничных точек воспользуемся формулой или .

.

Напомним, что множество называется замкнутым, если его дополнение открыто, т.е. - замкнуто . Возьмем список открытых множеств и, используя дополнения, составим список замкнутых множеств .

.
Ответ: , , , .

Теорема 6. Пусть А – подмножество топологического пространства (Х, Ф). Тогда:

1) 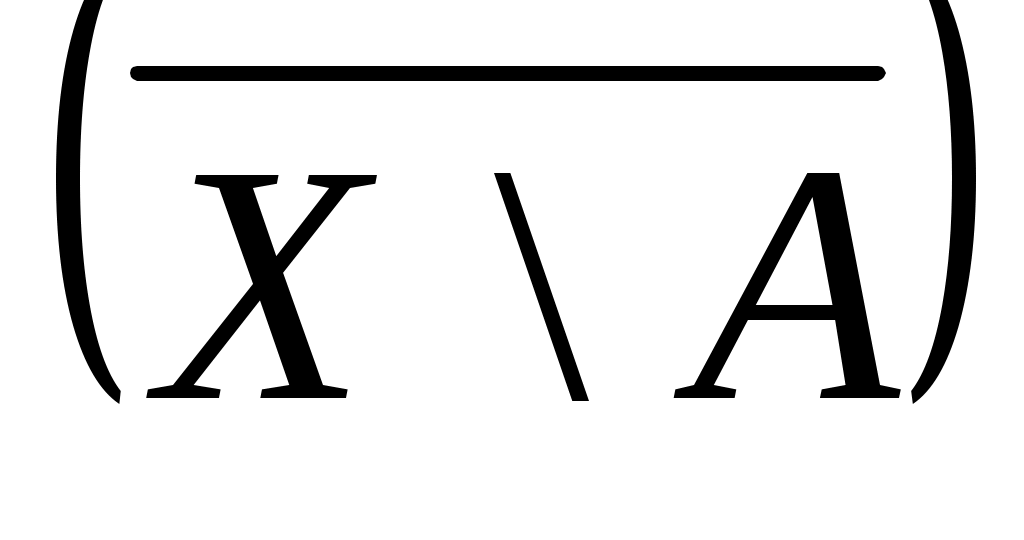А =  = \ int A.

2) Х \ A = int A  int (Х \ A).

3) = А  А, int A = А \ А.

4) А =  А  А.

А = int А  А  А =  .

Доказательство непосредственно следует из определения , int A, ext A и А.

Определение 10. Множество H называется всюду плотным в топологическом пространстве (Х, Ф), если = X.

Множество А называется нигде не плотным в пространстве(Х, Ф), если дополнение к замыканию А всюду плотно в Х, то есть = Х

Теорема 7. Пусть H  X, Ф = G 

Тогда = Х  H    для любого   .

Доказательство.

1) = Х. Тогда для произвольного открытого множества имеем  .

Если х₀  , то х₀  . Но, согласно определению точки прикосновения, имеем

 H  

2) Пусть для любого  :  H  .

Покажем, что Х  . Действительно, если х₀  Х и х₀  H, то для любой окрестности точки х₀ имеем:

 H  ,

а это значит, что

х₀  и Х  .

Так как всегда  Х, то Х = .