Начальный курс топологии. Учебнометодическое пособие Редактор И. Н. Никитина

• Название: Учебнометодическое пособие Редактор И. Н. Никитина
• Анкор: Начальный курс топологии
• Дата: 31.01.2022
• Размер: 4 Mb.
• Имя файла: Начальный курс топологии.doc
• Тип: Учебно-методическое пособие; #347044
• страница: 1 из 8

КУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра геометрии

В.А. Долженков, Е.Г. Соловьева, И.В. Горчинский
ЭЛЕМЕНТЫ ОБЩЕЙ ТОПОЛОГИИ

Курск 2006

Печатается по решению редакционно-

издательского совета университета
Элементы общей топологии: Учеб.-метод. пособие / сост. В.А. Долженков, Е.Г. Соловьева, И.В. Горчинский − Курск: Курск. гос. ун-т, 2006. – 63 с.


Данное учебно-методическое пособие предназначено для студентов 1-го курса специальности 351500 «Математическое обеспечение и администрирование информационных систем» по курсу «Геометрия и топология» (количество часов 400).

Пособие содержит теоретический и практический материал по теме, примеры выполнения контрольных заданий.

Рецензенты Лоторева И. В., канд. физ-мат наук

Фрундин В.Н., канд. пед. наук

ã Долженков В.А., Соловьева Е.Г., Горчинский И.В., сост. 2006

ã Курский государственный университет, 2006

Составители
Виктор Анатольевич Долженков

Елена Георгиевна Соловьева

Игорь Викторович Горчинский

Элементы общей топологии
Учебно-методическое пособие


Редактор И.Н.Никитина

Лицензия ИД № 06248 от 12.11.2001 г.

Подписано в печать 10.03.2006. Формат 60х84/16. Печать офсетная. Усл. печ. л. 3,9. Тираж 30 экз. Заказ .

Курский государственный университет

305000, г. Курск, ул. Радищева, 33

Отпечатано в лаборатории

информационно-методического

обеспечения КГУ
Оглавление
Введение.

Глава 1. Элементы общей топологии ……………….....4

§ 1. Метрическое пространство ………………… 4

§ 2. Определение и примеры топологических пространств …………..9

§ 3. Понятие подпространства. Замкнутые множества.

Внутренние, внешние и граничные точки ……………….... 12

§ 4. Базис. Аксиомы отделимости …………….........19

§ 5. Компактность топологических пространств. Связность

топологических пространств ………………….22

§ 6.Топологические преобразования топологических пространств …31

Глава 2. Топологические свойства поверхностей

§ 1. Понятие двумерного многообразия ………………….39

§ 2. Эйлерова характеристика поверхности ………………….43

§ 3. Ориентируемые и неориентируемые поверхности ……………….49 Решение нулевого варианта контрольной работы ………….….....53

Тест по курсу топология …………….....57

Список литературы ………………62

ВВЕДЕНИЕ
В топологии впервые даются строгие определения таких фундаментальных понятий геометрии, как линия и поверхность. Предметом топологии являются свойства фигур, сохраняющиеся при гомеоморфизмах, то есть взаимно однозначных и непрерывных в обе стороны отображениях. Топология, как наука возникла из потребностей связанных с математическим анализом. Эта наука, хотя и считается молодой, на самом деле известна уже давно, именно благодаря тесным связям с математическим анализом.

Геометрия школьного курса имеет дело в основном со свойствами фигур, связанными с понятиями длины, площади, объема – то есть метрическими свойствами фигур. Лишь очень немногие теоремы и задачи школьного курса геометрии рассматривают свойства иного характера. Топология как раз и является разделом геометрии, изучающим свойства фигур, которые могут быть установлены без измерения и сравнения величин, но при этом имеющие геометрический смысл.

Глава 1. ЭЛЕМЕНТЫ ОБЩЕЙ ТОПОЛОГИИ

§ 1. МЕТРИЧЕСКОЕ ПРОСТРАНСТВО
Определение 1. Декартово произведение множеств А и В определяется как множество всех упорядоченных пар (х, у), где хА, уВ, то есть

АВ = (х, у)| хА, уВ.

В частности, возможно А = В.

Определение 2. Говорят, что в множестве Х задана метрика , если определено отображение

: Х  Х  R,

удовлетворяющее следующим аксиомам:

1.  х, у  Х   (х, у)  0, причем  (х, у) = 0  х = у.

2.  х, у  Х   (х, у) =  (у, х).

3.  х, у, z  Х {  (х, у) +  (у, z)   (х, z)}.

Условия 1, 2, 3 называются аксиомами метрики, при этом условие 2 называется аксиомой симметрии, а 3 – аксиомой треугольника.

Определение 3. Множество Х с заданной на нем метрикой  называется метрическим пространством и обозначается ( Х, ).

В тех случаях, когда ясно, о какой метрике идет речь, метрическое пространство ( Х,) обозначают просто Х.

Число (х, у) называют расстоянием между точками х и у в пространстве Х.
ПРИМЕРЫ МЕТРИЧЕСКИХ ПРОСТРАНСТВ

Пример 1.Определим для элементов произвольного непустого множества Х расстояние следующим образом:

(х, у) = .

Очевидно, аксиомы 1 – 3 выполняются, а, следовательно, ( Х, ) - метрическое пространство.

Пример 2. Множество действительных чисел R с расстоянием

(х, у) = | х – у | является метрическим пространством.

Действительно,

(х, у) = | х – у |  0,

(х, у) = | х – у | = | у – х | = (у, х).

| x - y | + | y – z |  | x – y + y – z | = | x – z |,

| x - y | + | y – z |  | x – z |,

то есть все аксиомы метрического пространства выполняются.
Пример 3. Множество действительных чисел R с расстоянием

(х, у) = (у – х)² не является метрическим пространством.

Действительно не выполняется третья аксиома. Например, для трех точек 2, 3 и 4 получим:

(2, 3) = (3 – 2)² = 1, (3, 4) = (4 – 3)² = 1,

(2, 4) = (4 – 2)² = 4 и (2, 3) + (3, 4) < (2, 4).
Пример 4. Точками евклидова пространства являются всевозможные упорядоченные множества из действительных чисел .

Пусть .

Докажем, что - метрическое пространство.

Действительно, .
Пусть

.

Следовательно, аксиома 1) выполнена.

Так как выполняется равенство

,

то аксиома 2) выполнена.

Покажем, что в выполнена и аксиома треугольника.

Пусть , , , тогда аксиома треугольника записывается в виде
. (1)
Полагая , , получаем , а неравенство (1) принимает при этом вид
(2)
Но это неравенство сразу следует из известного неравенства Коши – Буняковского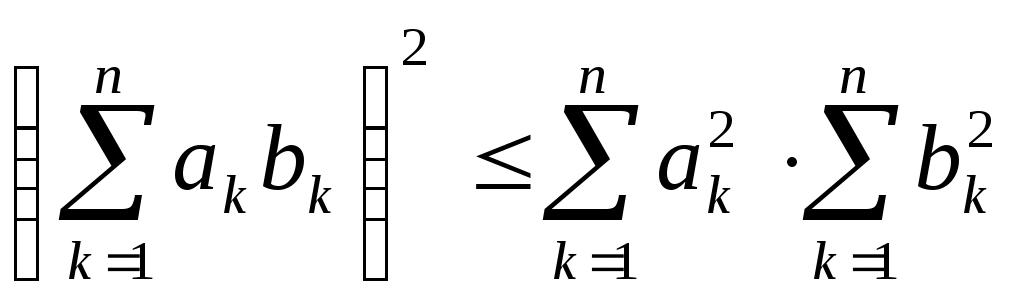

. (3)

Действительно, в силу этого неравенства имеем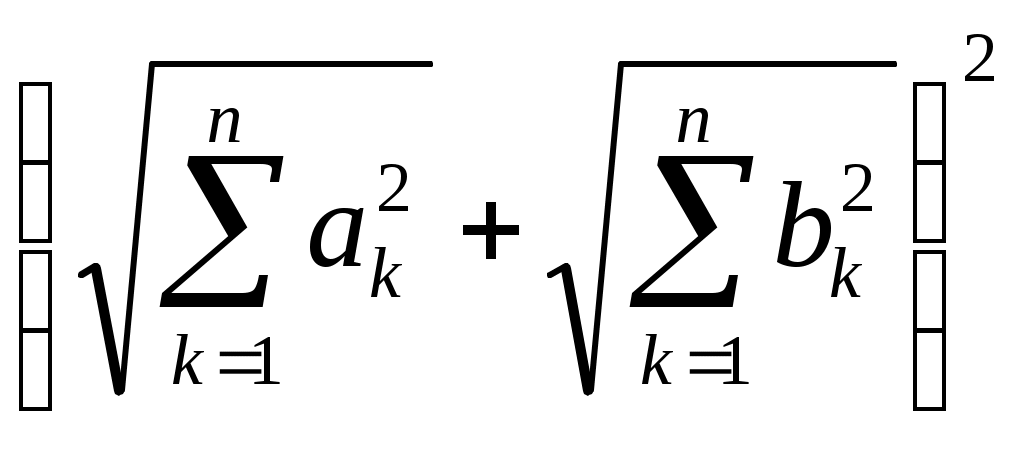




тем самым неравенства (2) и (1) доказаны.
Пример 5. Множество C_[a,b] всех непрерывных действительных функций, определенных на [ a, b ] с расстоянием
 (f, g ) = | g(t) – f(t) |

является метрическим пространством.
Действительно, из определения расстояния

 (f, g ) = | g(t) – f(t) |

непосредственно следует:

1. 
    (f, g )  ,  (f, g )   f = g.
   
2. 
    (f, g)   (g , f).
   
3. 
   Пусть f, g , h – непрерывные функции на  а , b .
   

Тогда

| f – g | , | f – h | , | g – h | –

так же непрерывные функции на промежутке  а , b . Из курса математического анализа известно, что на сегменте они достигают максимума. Пусть

| f (t₀) – g ( t₀ ) | = | f (t) – g (t) |,

| f (t₁) – h (t₁) | = | f (t) – h (t) |,

| h (t₂) – g (t₂) | = | h (t) – g (t) |.

Тогда

| f (t₀) – g ( t₀ ) | = | f (t₀) – h (t₀) + h (t₀) - g ( t₀ ) | 

 | f (t₀) – h (t₀)| + |h (t₀) - g ( t₀ ) | 

 | f (t₁) – h (t₁) | +| h (t₂) – g (t₂) | ,

то есть

 (f, g )   (f, h ) + (h, g).

Таким образом, третья аксиома выполняется, задача решена.
Определение 4. Пусть (Х, ) – метрическое пространство, х₀  Х, r >  - действительное число. Назовём открытым шаром с центром в точке х₀ и радиусом r множество
U (x₀, r) = x | x  X,  (x, x₀)  r .

Определение 5. Подмножество G  Х будем называть открытым в

(Х, ), если любая его точка является центром некоторого открытого шара, содержащегося в G.

Пустое множество  также считаем открытым множеством.

Определение 5. Окрестностью точки А метрического пространства будем называть любое открытое множество, содержащее эту точку.

Обозначим совокупность всех открытых множеств в (Х, ) просто Ф_.

Тогда имеет место следующая теорема.

Теорема. 1) Объединение любой совокупности { G_} множеств из Ф_ принадлежит Ф_.

G  Ф_.

2) Пересечение любых двух множеств G₁ и G₂ из Ф_ принадлежит Ф_.

G₁ G₂  Ф_.

3) Метрическое пространство Х - открытое множество, то есть

Х  Ф_ ,   Ф_.

Доказательство. 1) Пусть . Обозначим

G = .

Возьмём произвольную точку х₀  G. Тогда существует такое ₀, что х₀  , и так как  Ф_, то найдётся число r₀, что

U (х₀, r₀ )  .

Так как G ₀  G , то U (х₀, r₀ )  G.

Итак, G - открытое множество.

2) Пусть G = G₁  G₂ , где G₁, G₂  Ф_ и G .

Если х₀  G, то х₀  G₁ и х₀  G₂.

Тогда существуют такие радиусы r₁ и r₂ , что

U(х₀, r₁)  G_1, U(х₀, r₂)  G₂.

Обозначим r = min {r₁, r₂}, тогда

U (х₀, r)  G₁  G₂ = G.

Итак, G – открытое множество.

3. Так как всегда можно представить

Х = ,

где U_ - открытый шар радиуса r, с центром в точке , объединение рассматривается по всем точкам пространства, то в силу 1 получим, что пространство Х – открыто. Пустое множество мы предполагаем всегда открытым.

В дальнейшем описанное нами семейство Ф_ всех открытых множеств в метрическом пространстве (Х, ) будем называть топологией, индуцированной метрикой  в Х ._.

Теорема 2. Для любых двух различных точек метрического пространства (Х, ) существуют их непересекающиеся окрестности.

Доказательство. Пусть и (Х, ). Тогда между точками и определено расстояние (по свойству метрики). Взяв , рассмотрим открытые шары и . Легко показать, что . В самом деле, предположим противное. Тогда для точки имели бы , что невозможно. Следовательно, предположение неверно.

Теорема доказана.
§ 2. ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ ТОПОЛОГИЧЕСКИХ

ПРОСТРАНСТВ

Многие понятия теории метрических пространств (предел, предельная точка, точка прикосновения, замыкание множества, граница множества, непрерывность и т. д.) вводятся, опираясь на понятие окрестности или, что тоже самое, на понятие открытого множества. Понятие окрестность и открытое множество определяются с помощью метрики.

Можно стать на другой путь и, не вводя в данном множестве Х метрику, непосредственно определить в Х систему открытых множеств посредством введения аксиом.

Свойства открытых множеств метрического пространства принимаются в качестве аксиом. Этот путь приводит нас к топологическим пространствам, по отношению к которым метрические пространства представляют собой частный случай.

Определение 1. Пусть Х – непустое множество элементов произвольной природы, Ф = { } – семейство подмножеств множества Х, удовлетворяющее следующим аксиомам:

1. Само множество Х и пустое множество  принадлежат семейству Ф.

2. Объединение любого семейства множеств из Ф также принадлежит Ф.

3. Пересечение любых двух множеств из Ф также принадлежит Ф.

Тогда семейство Ф называется топологией или топологической структурой.

Пара (Х, Ф) или, другим словами, множество Х, в котором задана некоторая топология, называется топологическим пространством.

Элементы множества Х называются точками топологического пространства, элементы семейства Ф называются открытыми множествами в (Х, Ф).

Когда не может возникнуть недоразумений, разрешается просто писать: Х – топологическое пространство, G – открытое множество, то есть не указывать постоянно связь с топологией Ф.

Примеры топологических пространств.

Пример 1. Х – произвольное множество. Из аксиомы 1 топологического пространства вытекает, что среди открытых множеств любой топологической структуры в Х обязательно должны быть пустое множество  и само множество Х. Очевидно, что для семейства

Ф_т = {, X},

которое состоит лишь из этих двух множеств, выполняются также и аксиомы 2 и 3.

Поэтому Ф_т = {, X} является простейшей топологической структурой в Х. Эта топология называется тривиальной, а пара (Х, Ф) тривиальным топологическим пространством. Иногда эту пару называют антидискретным топологическим пространством.

Пример 2. Другой крайностью является так называемое дискретное топологическое пространство (Х, Ф_d), где Ф_d представляет собой семейство всех подмножеств множества Х. Очевидно, что и в этом случае все аксиомы 1 – 3 выполняются.

Пример 3. Двуточечное топологическое пространство:

Х = , Ф = {, Х, }.

Проверить выполнение аксиом 1 – 3 самостоятельно.

Пример 4. Пусть Х = R³. Открытыми в Х множествами назовем только открытые шары U(r) с общим центром О и радиусом r , а также всё множество Х и пустое множество.

Очевидно, аксиома 1 выполняется.

Пусть {U(r_)} – любая система открытых множеств. Тогда их объединением будет шар с центром О и радиусом r = .

Если = , то U(r) = X.

Следовательно, аксиома 2 выполняется.

Пересечением двух множеств U(r₁) и U(r₂) будет множество U(r), где r = , то есть аксиома 3 также выполняется.

Выделенное нами семейство открытых множеств является топологией в R³, которую иногда называют концентрической.

Пример 5. Пусть множество – квадрат, т.е. множество точек на плоскости, координаты которых связаны соотношениями и . Под открытыми множествами будем понимать пустое множество, множество , а также «полосы», т.е. множество точек , первые координаты которых связаны соотношением: , где . Будет ли топологическим пространством?

Решение.

П о условию задачи имеем , где . Проверим, будет ли семейство удовлетворять трем аксиомам топологии. Первая из них выполняется по условию. Проверим вторую аксиому: , где .

Следовательно, вторая аксиома выполняется. Проверим третью аксиому:

, где .

Третья аксиома топологии выполнена. Следовательно, пара – топологическое пространство.

Пример 6. Пусть – бесконечное множество, и состоит из , и тех подмножеств , дополнения которых конечны. Доказать, что – топологическое пространство.

Доказательство. , где и – конечное множество. Проверим, что совокупность множеств удовлетворяет трем аксиомам топологии. Первая из них выполняется тривиально. Для проверки второй и третьей аксиом воспользуемся формулами двойственности (де Моргана). Для проверки второй аксиомы получаем: – пересечении конечных множеств конечно, следовательно, , и вторая аксиома выполнена. Для проверки третьей аксиомы предположим, что и поэтому множества и конечные. Тогда также конечное множество, но оно равно 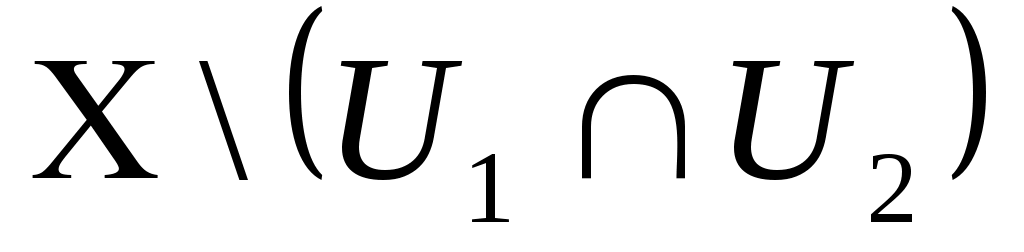и, таким образом, . Следовательно, - топологическое пространство.
Пример 7. Х = {0, 1, 2}, А = {0, 1} , B = {1, 2}, Ф = {, X, A, B}.

Очевидно Ф – не является топологической структурой, так как

А В = {1}  Ф.

Примеры показывают, что в любом не пустом множестве Х можно ввести топологию. При этом в одном и том же множестве Х можно определить разные топологии и получить различные топологические пространства.

Определение 2. Пусть в множестве Х введены две топологии Ф₁ и Ф₂. Говорят, что Ф₁ сильнее Ф₂ ( или Ф₂ слабее Ф₁ ), если Ф₂  Ф₁, то есть любое множество из Ф₂ принадлежит Ф₁.

Очевидно, самой сильной топологией является дискретная топология, а самой слабой – тривиальная.

А вообще – две топологии на одном и том же множестве могут быть несравнимыми.

Пример.

Х = ,

Ф₁ =  Х, ,

Ф₂  , Х, .

Топологии Ф₁ и Ф₂ несравнимы.
Теорема 1. Пересечение произвольного множества топологий, заданных на Х, является топологией в Х. Эта топология Ф слабее любой из данных топологий Ф .

Доказательство. Пусть .

Так как для любого 

{ Х   Ф ,

то

{ X   Ф.

Далее, из того, что каждое Ф замкнуто относительно взятия любых объединений и конечных пересечений, следует, что этим свойством обладает и множество .

Теорема 2. Пусть А – произвольная система подмножеств множества Х. Тогда существует минимальная топология в Х, содержащая А.

Действительно, всегда существуют топологии, содержащие А, например, дискретная. Пересечение всех топологий, содержащих А и есть искомая топология. Эта минимальная топология называется топологией, порождённой системой А.