Начальный курс топологии. Учебнометодическое пособие Редактор И. Н. Никитина
 Скачать 4 Mb.
|
|
§ 2, пример 4 ). Доказать, что (Х, Фк) некомпактное топологическое пространство, но любое ограниченное замкнутое множество Н этого пространства является компактным подмножеством. Доказательство. Пусть { G}А - произвольное открытое покрытие множества Н. По определению топологии каждое G есть открытый шар с центром в точке О. Следовательно, мы имеем множество вложенных друг в друга открытых шаров, радиусы которых возрастают неограниченно: r1, r2, …, r, … . Предположим, что нам удалось выбрать конечное подпокрытие G1, G2, …, Gк из покрытия { G}А. При этом мы вполне можем считать, что G1 G2 … Gк . Тогда соответствующие радиусы этих шаров удовлетворяют неравенствам : r1 r2 … rк . Но открытый шар любого конечного радиуса не покрывает все пространство. Следовательно, предположение неверно. Докажем вторую часть задачи. Пусть Н ограниченное замкнутое множество в (Х, Фк). Обозначим rх = | Ох |, где х Н, r0 =  .Предположим, что мы имеем произвольное открытое покрытие { G}А множества Н. Как и в первой части задачи мы имеем множество вложенных друг в друга открытых шаров, радиусы которых возрастают неограниченно: r1, r2, …, r, … . Рассмотрим все радиусы r r0. Обозначим  наименьший радиус. Тогда r0 и открытый шар  из покрытия { G}А одновременно будет представлять конечное покрытие Н. Согласно теореме 1 множество Н будет компактным множеством.Связность топологических пространств Определение 1. Топологическое пространство (Х, Ф) называется несвязным, если существуют два непустых открытых множества U и V таких, что U V = Х и U V = . Другими словами топологическое пространство (Х, Ф) может быть разбито на два непустых открытых множества, не имеющих между собой общих точек. Топологическое пространство (Х, Ф) называется связным, если не существует такого разбиения. Пример. Х= (  , b) , (X, Ф) – связное топологическое пространство, если Ф = , Х, и, если Ф = , Х, , b– то это пример несвязного топологического пространства.Заметим, что если несвязное пространство Х разбито на два непустых открытых множества U и V , U V = , то U = Cx V и V = Cx U . Поэтому U и V – замкнутые множества. Отсюда получаем необходимые и достаточные условия. Теорема 1. Топологическое пространство (X, Ф) будет связным тогда и только тогда, когда в нем одновременно открытым и замкнутым множеством являются лишь само пространство или пустое множество. Определение 2. Множеством М в топологическом пространстве называется связным, если оно является связным пространством относительно индуцированной топологии, то есть связно определяемое им подпространство. Другими словами, множеством М в топологическом пространстве Х называется связным, если нельзя найти двух открытых в Х множеств G1 и G2 таких, что (G1 М) (G2 М) = М. (G1 М) (G2 М) = . G1 М , G2 М . Теорема 2. В топологическом пространстве (Х, Ф) замыкание связного множества – связно. Доказательство. Пусть H – связное множество в топологическом пространстве Х. Предположим, что  - несвязно, тогда существуют открытые в Х множества U и V такие, что = ( U) ( V),( U) ( V) = , U , V .Так как H ,то H (V ) = H V,H (U ) = H U,H = H = H (( U) ( V))= = (H ( U)) (H ( V))== (H U) (Н V). Следовательно, H = (H U) (H V). Кроме того, (H U) (H V) ( U) ( V) = ,поэтому (H U) (H V) = . Поскольку H всюду плотно в , то, как ранее доказано (§ 3, теорема 6),H U и H V . Итак, H – несвязное подмножество, что противоречит условию. Следовательно, предположение неверно и связное множество.Теорема 3. Если А и В два открытых множества в (Х, Ф), причем А В = и непустое связное множество H A B, то H A , или H В. Доказательство. Пусть H А и H В . Тогда, поскольку H A B, то H = H ( A B) = (H А) (H В). Так как (H А) (H В) A B =, то (H А) (H В) =. И, следовательно, Н – несвязное множество. Таким образом, получили противоречие с условием теоремы. Теорема доказана. Теорема 4. Пусть  - совокупность связных подмножеств в пространстве (Х, Ф), имеющих общую точку. Тогда множество H =  также будет связным в (Х, Ф). Доказательство. Предположим противное. Тогда существуют U и V – открытые в (Х, Ф) множества такие, что (U H) (V H) = H, (U H) (V H) = , U H , V H . Тогда, для любого имеем: = H == ((U H) (V H)) == ( U H) ( V H ) == ( U) ( V).Таким образом, = ( U) ( V).Учитывая, что U и V – открыты в , получим ( U) ( V) (H U) (H V) = .Но, так как - связно, то согласно теореме 3, либо U = ,либо V = ,то есть каждое содержится либо в U, либо в V. Предположим, что H  U,  V.Тогда H (H U) (H V) = .Но это противоречит условию, так как у них есть общая точка. Итак, для любого либо все U , либо все V.Предположим, что U = ,тогда H U  ( U) = ,а это противоречит условию (3). Теорема доказана. Пусть теперь – произвольная точка топологического пространства(Х, Ф). {Н  } – совокупность всех связных множеств, каждое из которых содержит точку . Тогда согласно теореме 4H = является наибольшим связным множеством, содержащим точку , то есть такое, которое содержит любое связное подмножество, содержащее точку .Это наибольшее связное множество, содержащее точку , называется компонентой точки в топологическом пространстве (Х, Ф).Если Н  и Нb – компоненты точек и  , и Н Нb ,то Н Нb = Н = Нb,так как Н Нb - связное множество, а Н и Нb – компоненты связности.Поэтому справедлива следующая теорема. Теорема 5. Компоненты двух различных точек либо не пересекаются, либо совпадают. Теперь мы можем говорить просто о компонентах пространства, на которые они распадаются. Теорема 6. Компонента топологического пространства (Х, Ф) является замкнутым множеством. Доказательство. Пусть Н – компонента топологического пространства (Х, Ф), и – некоторая ее точка.Очевидно Н  , В силу теоремы 2 множество – связно и так как , то Н.Поэтому = Н.Замечание. Пусть топологическое пространство (Х, Ф) – несвязное, то есть существуют два непустых открытых множества U и V таких, что U V = Х и U V = . Если при этом различные точки х и у принадлежат одной компоненте, то {x, y} U или {x, y} V. Это утверждение вытекает из теоремы 3. Определение 3. Областью называется непустое связное открытое множество топологического пространства. Замкнутой областью называется такое замкнутое множество, которое является замыканием области. Пример 1. Пусть Х - множество действительных чисел с топологией  . Доказать, что любое подмножество  связно.Доказательство. Рассмотрим произвольное подмножество  . Пусть  – непустое подмножество  , открытое и замкнутое в . Тогда =  ,где  открыто в , а  замкнуто в Х, т.е.  для некоторого  , а  для некоторого  . Так как ,то для любого  выполнены неравенства  и  . Действительно, если найдется значение  , то  . Аналогично, если найдется значение  , то  . Итак,  и  , откуда следует, что связно.Пример 2. Доказать, что множество рациональных чисел  на прямой R несвязно.Доказательство. Пусть  – произвольное иррациональное число. Тогда множества  и  не пусты, открыты и не пересекаются. Таким образом, разложение  означает несвязность  .Пример 3. Доказать, что отрезок  числовой оси R связное множество.Доказательство. Рассмотрим топологическое пространство  с топологией R. Предположим, что Х несвязно:  ,где  не пустые и открытые (и одновременно замкнутые) множества. Пусть  . Будем рассматривать отрезки  , где   . Когда  близко к , то  , так как открыто. Точную верхнюю грань этих значений обозначим через  , ясно, что  . Если  , то близкие к  точки (слева и справа) тоже лежат в , что противоречит определению . Следовательно,  . Однако, по определению невозможно включение  . Таким образом, получаем противоречие с равенством  .§ 6. ТОПОЛОГИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВ Непрерывные отображения Пусть даны топологические пространства (Х, Ф), (У, W) и отображение  : X У.Определение 1. Отображение 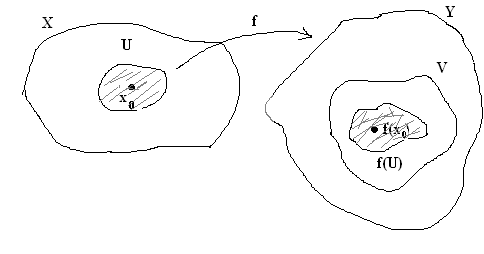: X У называется непрерывным в точке х0 Х, если для каждой окрестности V точки f(x0) существует такая окрестность U точки х0, что (U) V. Определение 2. Отображение : X У называется непрерывным на множестве Н Х, если непрерывно в каждой его точке.Если Н = Х, то говорят, что непрерывно на Х.Определение 3. Если : X У, В У, то множество всех точек х0 Х, для каждой из которых имеем (x0) В называется прообразом множества В, и обозначается -1(B), причем имеет место ( -1(B)) B.Теорема 1. Для того, чтобы отображение : X У было непрерывным на Х, необходимо и достаточно, чтобы прообраз любого открытого (замкнутого) множества был открытым (замкнутым) множеством.Доказательство. 1. Необходимость. Пусть : Х У непрерывно, V открытое множество в У, а U = -1(V).Докажем, что U – открытое множество в Х. Пусть  – любая точка из U и b = ( ). Множество V является окрестностью точки b. Так как – непрерывно, то найдётся окрестностью U точки , что (U ) V. Очевидно, U -1(V) = U.Так как U =  U , то U – открытое множество.Достаточность. Возьмём любую точку Х и пусть b = ( ). Если V – произвольная окрестность точки b, то U = -1(V) открытое множество и является окрестностью точки . Поскольку (U) V, то – непрерывно в точке , что требовалось доказать.Для замкнутых множеств теорема доказывается переходом к дополнительным множествам. Замечание. При непрерывном отображении образ замкнутого ( открытого ) множества может быть не замкнутым ( не открытым ) множеством. Пример. Отображение =  плоскости Х в плоскость U , с естественными топологиями, отображает полупрямую (замкнутое множество)  на множество  которое не является замкнутым множеством в U. 2. Постоянное отображение, как правило, дает пример, в котором образ открытого множества не будет открытым. Теорема 2. Пусть X, Y, Z – топологические пространства. Если отображения f  и g  непрерывны, то непрерывна и их композиция:g f : Х Z. Доказательство. Пусть W открытое множество пространства Z . Так как g – непрерывно, то по предыдущей теореме G -1(W) = V – открыто в У. 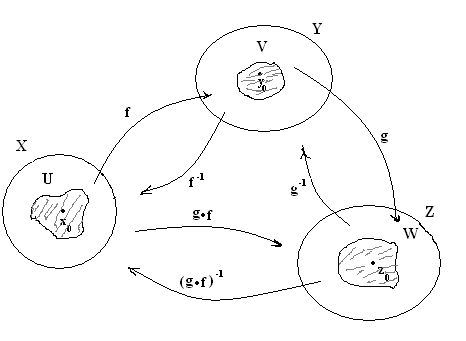 Тогда аналогично, U = f-1(V) – открыто в Х. Но U = f -1 (g -1(W)) = ( gf ) -1(W) – прообраз W. Теорема доказана. Примеры непрерывных отображений Пример 1. Рассмотрим плоскость П и прямую ℓ П с естественными топологиями. Докажем, что ортогональное проектирование  : П ℓ является непрерывным отображением.Действительно, пусть для произвольной точки А П 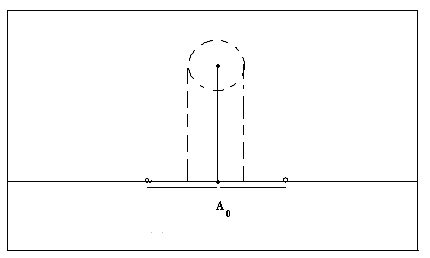(А) = А0.Пусть V–  -окрестность точки А0 , то есть V – интервал.  В точке А рассмотрим открытый круг радиуса =  , то есть окрестность U точки А. Очевидно, (U) V и ,следовательно, – является непрерывным отображением в точке А.Так как А – произвольная точка плоскости П, то – непрерывное отображение.Пример 2. Если Х, У – топологические пространства и : Х У непрерывное отображение, то образ связного множества Х Х является связным множеством У У.Решение. Предположим противное, что образ связного множества Х является несвязным множеством У, то есть состоит из двух множеств У1 и У2 , и при этом У1 У2 . Согласно определению несвязного множества можно считать, что У1 и У2 – открытые множества в топологии, индуцированной на ( Х ).Тогд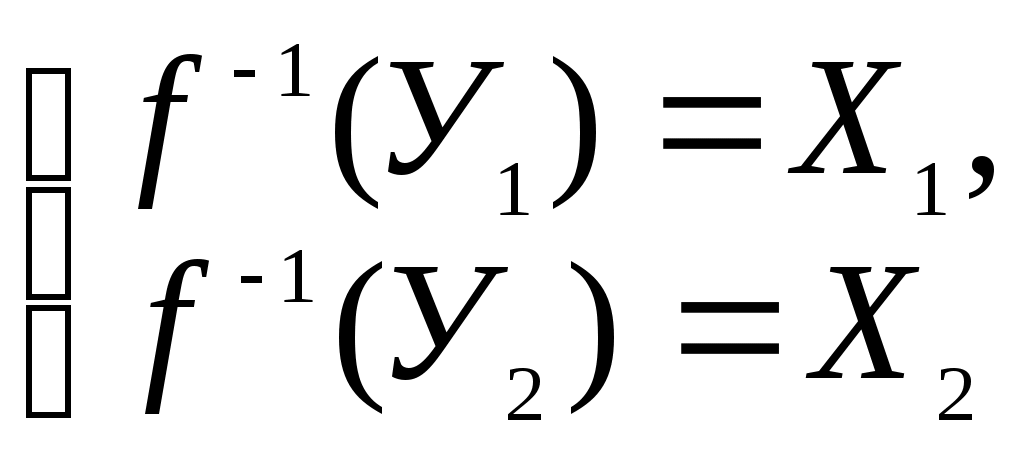а,  открытые множества в Х. Так как при этом Х1 Х2 = , Х1 , Х2 , Х1 Х2 = Х, то Х – несвязное множество. Полученное противоречие доказывает утверждение. Теорема 3. Если Х – компактное топологическое пространство, У – топологическое пространство и : Х У непрерывное отображение, то (Х) компактно в У.Доказательство. Пусть  = G – открытое покрытие множества (x) в У.В силу теоремы 1 каждое множество U = -1 (G ) будет открытым в Х, а U – открытое покрытие множества Х. В силу компактности Х, можно выбрать конечное подпокрытие Х U1, U2,…, Uk. Соответственно, получаем конечное подпокрытие G1, G2, … ,Gk множества ( X ).В силу теоремы 1 § 6 множество (X ) – компактно.Теорема 4. Если – непрерывное отображение компактного пространства Х в хаусдорфово пространство У, то образ (F) любого замкнутого множества F X – замкнут в У.Доказательство. В силу теоремы 2 § 6 множество F в Х компактно. В силу теоремы 3 § 6 множество (F) – компактное в У.В силу теоремы 4 § 6 множество (F) – замкнутое в У.Топологические отображения Определение 4. Пусть даны топологические пространства Х и У. Отображение : Х У называется топологическим (гомеоморфизмом), если – биекция и, при этом, отображения и -1 – непрерывные. Свойство 1. Всякое тождественное отображение е: Х Х является гомеоморфизмом. Доказательство непосредственно вытекает из определения. Свойство 2. Если X, У, Z - топологические пространства, а отображения : Х У ,g : У Z являются топологическими, то и их композиция g : Х Z – также топологическое отображение.Действительно, композиция биекций является биекцией. Произведение непрерывных отображений является непрерывным отображением. Обратным к g : ХZ отображением является отображение(g ) -1 = -1 g -1.Так как отображения : Х У,g : У Z являются топологическими, то обратные к ним отображения -1: У Х , g -1: Z У являются непрерывными. Поэтому и их композиция -1 g -1 – непрерывное отображение, а следовательно, и отображение (g )-1 непрерывное.Свойство доказано. Свойство 3. Если : Х У - гомеоморфизм, то и -1: У Х - гомеоморфизм.Доказательство. Действительно, так как : Х У – гомеоморфизм, то – биекция. Поэтому обратное к нему отображение -1 также биекция. При этом, согласно условию -1 – непрерывно. Учитывая, что ( -1) -1 = ,имеем: отображение --1 – гомеоморфизм.Свойство доказано. Определение 5. Говорят, что топологическое пространство Х гомеоморфно топологическому пространству У, если существует гомеоморфизм : Х У. Учитывая выполнимость перечисленных выше свойств гомеоморфизма, получим, что отношение гомеоморфности топологических пространств является отношением эквивалентности. Про гомеоморфные пространства также говорят, что они топологически эквивалентны. Обозначаем: Х  У.Кроме того, мы одновременно показали, что (с учётом ассоциативности произведения топологических отображений) множество всех гомеоморфизмов пространства на себя по умножению есть группа. В связи с этим свойства фигур, сохраняющиеся при гомеоморфизмах, называются топологическими, а топология изучает свойства фигур, инвариантные относительно гомеоморфных отображений топологических пространств. Таким образом, топология изучает геометрию группы всех гомеоморфизмов пространства на себя. Примеры гомеоморфных пространств и гомеоморфизмов Пример 1. Задана числовая прямая с естественной топологией. Доказать, что любые два интервала ( , b) и (c, d) гомеоморфные. Действительно, гомеоморфизм между ними устанавливается, например, линейной функцией у =  (х – ) + с,где х ( , b), а у (с, d).Пример 2. Задано трехмерное евклидово пространство с топологией, порожденной метрикой. Доказать, что сфера гомеоморфна поверхности куба. Для того, чтобы установить гомеоморфизм между ними, достаточно поместить их центры в одну точку и произвести из неё центральное проектирование. 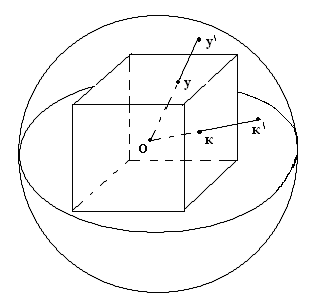 Пример 3. Задана числовая прямая с естественной топологией. Доказать, что интервал и прямая гомеоморфные. Гомеоморфизм между ними можно установить следующей функцией: у = tg  х Х = (а, b), у У = R. Пример 4. Пусть U = U / 0 U 2 , S = S (0, 1) – окружность радиуса 1 с центром в начале координат. На U и на S рассматриваем топологии, индуцированные топологией плоскости. Рассмотрим отображение : U S,где :  Является ли отображение – гомеоморфизмом ?Решение. Покажем, что – биекция. Действительно, – отображение. В силу свойств тригонометрических функций, если u1 u2, то (х1, у1) (х2, у2), и, следовательно, 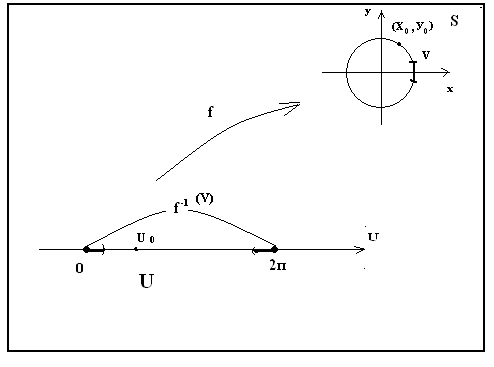– инъективное отображение. Для любой точки М (х0, у0) S найдётся единственное значение u0 из промежутка [0, 2), что 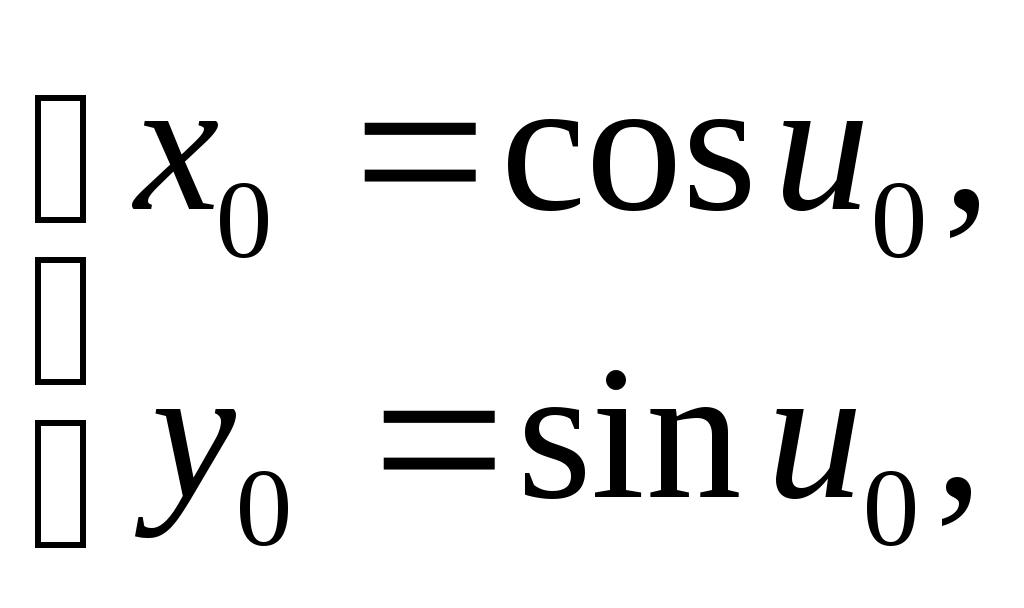 но это означает, что – сюръективное отображение. Итак, мы показали, что – биекция. В силу непрерывности тригонометрических функций – непрерывное отображение, однако, отображение -1 – не является непрерывным в точке (1, 0). Действительно, если взять связную окрестность V точки (1,0) на окружности S, то ее образ -1 (V) при отображении -1 будет несвязным на множестве U.Таким образом, не обязательно взаимно однозначное и непрерывное отображение топологического пространства Х на топологическое пространство У будет гомеоморфизмом, так как обратное отображение не обязано быть непрерывным. Однако, имеет место Теорема 5. Пусть : Х У – непрерывное взаимно – однозначное отображение и (Х) = У. Тогда, если Х – компактно, а У – хаусдорфово пространство, то – гомеоморфизм.Доказательство. Пусть F X – замкнутое множество, а H –прообраз F в У относительно отображения -1 : У ХВ силу теоремы 4 множество H = (F) – замкнутое множество, а согласно теореме 1 отображение -1 непрерывное, то есть – гомеоморфизм.Теорема доказана. ГЛАВА 2. ТОПОЛОГИЧЕСКИЕ СВОЙСТВА ПОВЕРХНОСТЕЙ § 1. ПОНЯТИЕ ДВУМЕРНОГО МНОГООБРАЗИЯ Важнейшим для геометрии классом топологических пространств являются двумерные многообразия. Определение 1. Двумерным многообразием называется хаусдорфово топологическое пространство со счетной базой, каждая точка которого имеет окрестность, гомеоморфную открытому кругу. Локально у двумерных многообразий те же топологические свойства, что и у евклидовой плоскости. В топологии под термином «поверхность» понимают именно двумерное многообразие. Поэтому в дальнейшее мы не будем различать эти два понятия. Примерами поверхностей являются любая область на евклидовой плоскости, сфера, эллипсоид, гиперболоиды, параболоиды в евклидовом пространстве с естественной топологией.  В дальнейшем мы часто будем встречать поверхность, которую называют тором. Поэтому определим ее следующим образом. Определение 2. Тором в пространстве Е3 называется множество точек, образованное вращением окружности вокруг оси, лежащей в плоскости окружности и не пересекающейся с этой окружностью. 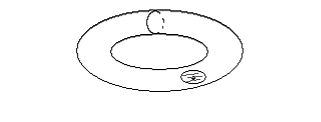 Компактные поверхности называют замкнутыми поверхностями. Например, сфера, тор – замкнутые поверхности, а параболоиды и гиперболоиды не являются замкнутыми поверхностями. Определение 3. Двумерным многообразием с краем или поверхностью с краем называется хаусдорфово топологическое пространство со счетной базой, каждая точка которого имеет окрестность, гомеоморфную открытому кругу или полукругу вместе с диаметром. Те точки поверхности с краем, у которых есть окрестность гомеоморфная открытому кругу, называются внутренними точками поверхности, а те ее точки, которые имеют окрестности, гомеоморфные полукругу вместе с диаметром, называются краевыми точками. В дальнейшем будем считать, что для данной поверхности внутренняя ее точка одновременно не может быть ее краевой точкой. Множество внутренних точек любой поверхности F с краем открыто в F и само является поверхностью. Поэтому множество точек края в F замкнуто и его обозначают F. Отметим, что F является границей в F множества внутренних точек. Каждая поверхность является частным случаем поверхности с краем, край которой пуст. Если край F поверхности с краем F не пуст, то он имеет простое строение: каждая его компонента гомеоморфна либо окружности, либо прямой. В частности, когда F компактна, то ее край состоит из конечного числа компонент, каждая из которых гомеоморфна окружности. Так, край кольца – это две окружности, край боковой поверхности цилиндра – также две окружности.  В дальнейшем мы будем часто сталкиваться с процессом построения новых поверхностей, который называют операцией склеивания. Эта операция заключается в следующем. Берутся две поверхности с краем F и F, и на их краях F и F выделяются некоторые гомеоморфные между собой части и . Соответствующие при данном гомеоморфизме точки Х и X отождествляются, т. е. считаются за одну точку Х. Одновременно склеиваются и их окрестности. При этом получается новая поверхность с краем, склеенная из поверхностей F и F. 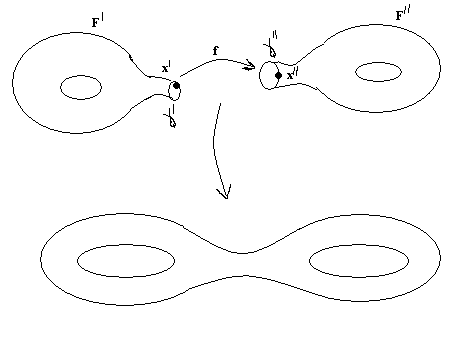 Например, многогранную поверхность можно считать склеенной из ее граней, а поверхность цилиндра вращения – склеенной из ее боковой поверхности и двух оснований. Склеивать можно и отдельные части края одной и той же поверхности с краем. Например, таким склеиванием получается поверхность, которую называют листом Мебиуса. Пример 1. Лист Мебиуса, как пример поверхности с краем был описан в 1862 1865 годах в работах немецких математиков Мебиуса и Листинга. Поверхность получается следующим образом. Лента прямоугольной формы один раз перекручивается, и затем ее концы склеиваются. Полученная поверхность с краем имеет лишь одну сторону. Например, перемещая кисточку по ленте Мебиуса, мы придем к тому же месту, с которого начинали закрашивание, но с обратной стороны. Перемещая кисточку дальше, мы закрасим всю ленту Мебиуса и убедимся, что у нее нет «второй стороны». 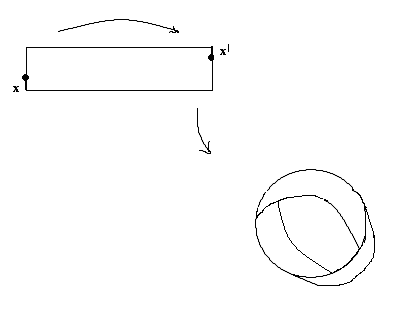 Край листа Мебиуса гомеоморфен окружности, поэтому Лист Мебиуса не гомеоморфен кольцу, у которого край состоит из двух окружностей. Пример 2. Если на торе вырезать круглую дыру, то мы получим поверхность с краем, которая называется ручкой. Край полученной поверхности состоит из одной кривой, гомеоморфной окружности. 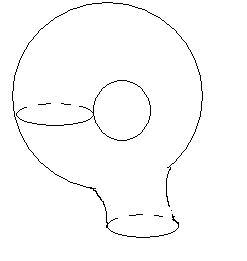 Пример 3. Рассмотрим сферу, в которой вырезано p круглых дыр, и заклеим каждую из дыр ручкой. Полученная поверхность называется сферой с p ручками. Сфера с одной ручкой гомеоморфна тору, а сфера с двумя ручками поверхности «кренделя» (получающейся склеиванием двух ручек). 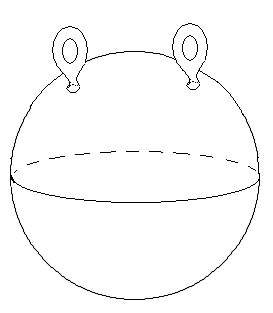 |