Начальный курс топологии. Учебнометодическое пособие Редактор И. Н. Никитина
 Скачать 4 Mb.
|
Классификация замкнутых поверхностейМы подходим к формулировке замечательной теоремы о топологической классификации поверхностей, полученной немецким математиком Мебиусом и французским математиком Жорданом. Условимся рассматривать только замкнутые поверхности (которые не имеют края и допускают разбиение на конечное число многоугольников). Плоскость, например, не является замкнутой поверхностью: конечный граф, начерченный на плоскости, не разбивает ее на области, которые все гомеоморфны кругу. Задача топологической классификации поверхностей заключается в том, чтобы указать такие попарно не гомеоморфные замкнутые поверхности, что любая замкнутая поверхность гомеоморфна одной из них. Иначе говоря, нужно перечислить все топологически различные замкнутые поверхности. Теорема. Обозначим через P0 сферу, а через Pk сферу с k ручками. Тогда поверхности P0, P1, P2, …, Pk ,… (1) дают полную топологическую классификацию замкнутых ориентируемых поверхностей, т.е. здесь перечислены все различные типы таких поверхностей. Замкнутую неориентируемую поверхность можно расположить в пространстве лишь с самопересечениями. Так как край ленты Мебиуса гомеоморфен окружности, то можно попытаться приклеить ленту Мебиуса своим краем к краю дыры, вырезанной в некоторой поверхности, например в сфере. Если на одной окружности кольца склеить между собой каждые две диаметрально противоположные точки, то мы получим ленту Мебиуса. Пусть теперь ℓ контур круглой дыры на некоторой поверхности Q. Вырежем из поверхности узкую полоску (кольцо) вокруг дыры ℓ и обозначим через ℓ′ наружный контур этого кольца . Тогда получится поверхность, гомеоморфная Q (только с несколько большей дырой ℓ′), и отдельно кольцо. Склеим теперь на контуре ℓ отрезанного кольца каждые диаметрально противоположные точки; тогда кольцо превратится в ленту Мебиуса. Эту ленту Мебиуса мы и вклеим в дыру ℓ′. В результате мы вклеим в поверхность Q (точнее, в поверхность, гомеоморфную ей) ленту Мебиуса. Но разрезание поверхности по контуру ℓ′ и обратное склеивание этого разреза можно было и не делать: достаточно было просто склеить на контуре ℓ каждые две диаметрально противоположные точки. Итак, склеивание каждых двух диаметрально противоположных точек на контуре круглой дыры равносильно вклеиванию в эту дыру ленту Мебиуса. Теперь мы можем сформулировать вторую половину теоремы МебиусаЖордана о классификации поверхностей, а именно, дать перечисление всех топологически различных типов замкнутых неориентируемых поверхностей. Теорема. Обозначим через Nq поверхность, получающуюся из сферы вырезанием в ней q дыр и заклеиванием их всех лентами Мебиуса. Тогда поверхности N1, N2, … , Nq, … (2) дают полную топологическую классификацию замкнутых неориентируемых поверхностей. Решение нулевого варианта контрольной работы Задание 1. Зафиксируем точку  в трехмерном евклидовом пространстве. Открытыми множествами назовем все пространство, пустое множество, а также внешние области шаров с центром в точке и произвольным радиусом  , т.е. множество всех точек  таких, что  . Показать, что данное пространство с указанными открытыми множествами является топологическим пространством.Решение. Пусть  - семейство всех открытых множеств данного пространства. Покажем, что - топология.По условию само множество и пустое множество принадлежат семейству .Покажем, что объединение любого числа множество  семейства также принадлежит , т.е. является открытым множеством.Пусть  рассматриваемое семейство множеств,  - радиус шара, определяющего множество . Рассмотрим соответствующее множество  . Так как  , то множество ограничено снизу, а значит, как известно из курса математического анализа, имеет точную нижнюю грань  . Тогда  . Так как  , то и  .Покажем, что пересечение любых двух открытых множеств  и  также принадлежит семейству .Пусть множество определяется шаром радиуса  , а множество - шаром радиуса  . Тогда  , где  - множество, определяемое шаром радиуса  . Так как  , то  . Таким образом рассматриваемое пространство с введенными открытыми множествами является топологическим пространством. Задание 2. Для множества  топологического пространства  с топологией  , индуцированной обычной метрикой, т.е.  , найти  ,  ,  ,  и множество всех изолированных точек, если  . Решение. Изобразим данное множество н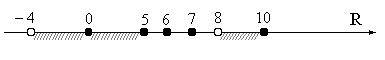а числовой оси.Р  ис. 1. Покажем, что  .Пусть  и  , тогда имеем:  , т. е. любая точка интервала  является внутренней. Для каждой из точек  не существует окрестности, входящей в .Рассмотрим множество  . И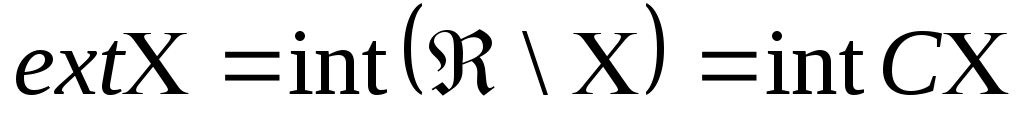з курса математического анализа известно, что любой числовой промежуток содержит бесконечно много как рациональных, так и иррациональных точек. Поэтому любая окрестность точки этого множества будет содержать иррациональные точки, т. е. точки, принадлежащие  и, следовательно, внутренних точек в этом множестве нет.Итак,  .2.  . . По аналогии с первым пунктом можно убедиться, что  . Итак,  .3. Известно, что  . Следовательно  .Так как замыкание  , то получаем:  .Покажем, что точки  являются изолированными. Для этого рассмотрим окрестности  и  . , .А это означает, что точки являются изолированными.Ответ: , , , , – множество изолированных точек.Задание 3. Доказать, что множество точек Х плоскости , имеющих только одну рациональную координату, несвязно. Решение. 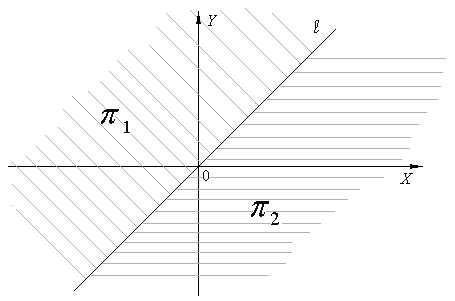 Рис. 2.Рассмотрим прямую  , все точки, которой не принадлежат множеству Х. Действительно, ее точки имеют либо две рациональные координаты, либо две иррациональные. Рассмотрим две открытые полуплоскости 1 и 2 с границей  . Пусть  и  . (1)Покажем, что множества  и  являются открытыми в подпространстве  с топологией  , где - открытое множество топологического пространства  .Пусть точка  . Рассмотрим число  и окрестность этой точки  , где  . Очевидно, что  (2).Рассмотрим окрестность этой точки  (3)в подпространстве  . В силу утверждений (1), (2) и (3) заключаем, что  , а это означает, что точка  является внутренней точкой множества , откуда следует, что  (4).Используя критерий открытого множества и равенство (4), можно утверждать, что - открытое множество подпространства . Нетрудно убедиться, что множество также является открытым в подпространстве . При этом  и  , откуда по определению несвязного подпространства следует, что - несвязное множество.Задание 4. Показать, что бесконечное множество точек числовой оси  с координатами  не является компактным.Решение. Рассмотрим данное множество как числовую последовательность  и рассмотрим его бесконечное открытое покрытие  , где  .При этом  .Таким образом, если из данного покрытия  удалить хотя бы одну окрестность  , то среди оставшихся окрестностей не найдется ни одной, содержащей точку  .Следовательно, по определению данное множество не является компактным. |